Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
 Скачать 4.07 Mb.
|
Лекция 12 Методы планирования эксперимента (часть 2)Во многих случаях достаточно рассмотреть всего два уровня факторов, влияющих на производственный процесс. Например, температура проведения химического процесса может быть установлена немного ниже или немного выше заданного уровня, количество растворителя при производстве красителя можно немного увеличить или уменьшить и так далее. Экспериментатор хотел бы установить, влияют ли какие-либо из этих изменений на результат производственного процесса. Наиболее очевидный подход в данном случае состоит в полном переборе комбинаций уровней интересующих факторов. Это отлично сработает, если бы число необходимых опытов в таком эксперименте не росло экспоненциально. Например, если вы хотите провести эксперимент с 7 факторами, то необходимое число опытов равно 2**7 = 128. Чтобы изучить 10 факторов вам потребуется 2**10 = 1,024 опытов. Поскольку для проведения каждого опыта нужна длительная и дорогостоящая перенастройка, то на практике часто нереально ставить столь большое число опытов. В этом случае при планировании эксперимента обычно используют дробные планы, отбрасывающие взаимодействия высокого порядка и уделяющие наибольшее внимание главным эффектам. Дробный факторный эксперимент. Другое название - метод дробных реплик. С увеличением количества факторов в ПФЭ резко возрастает число опытов и число степеней свободы. (см. таблицу 6.1.). Т.е. количество опытов в ПФЭ обычно превосходит число определяемых коэффициентов, т.е. ПФЭ обладает избыточностью опытов. В дробном факторном эксперименте (ДФЭ) в отличие от ПФЭ используются не все возможные сочетания уровней изучаемых факторов. Некоторые их сочетания пропускаются. Сокращение перебора уровней всегда приводит к потере части исходной информации. План ДФЭ строится так, чтобы обеспечить получение линейной модели, при этом необходимо, чтобы матрица планирования сохранила свойство ортогональности. Рассматриваемый метод заключается в том, что для получения математического описания используется часть ПФЭ. Например, при 4 факторах за основу берется план для трех факторов, а для четвертого фактора используется план, соответствующий одному из столбцов содержащих эффекты взаимодействия (столбцы 6-9 в таблице 6.3.). Если нет сведений о значимости взаимодействий факторов, то лучше выбрать столбец 9, соответствующий тройным взаимодействиям  или  , такие соотношения называют генерирующими соотношениями, так как они генерируют (создают) дробную реплику. Умножая обе части генерирующего соотношения на  получаем  , называемое определяющим контрастом. Эксперимент проводят по плану (таблица 12.1):
По этому плану, например, для первого опыта:     , результат опыта  . План содержит половину опытов ПФЭ 24 и носит название полуреплики. Используют также ¼ реплики, ⅛ реплики и т.д. Обозначаются ДПЭ в виде 2k-p, где k – количество факторов, p –число дробных реплик, в нашем примере это 24-1. Расчет коэффициентов регрессии, проверка их значимости производят по тем же формулам, что и для ПФЭ. Подведем итог. Планы дробного факторного эксперимента (планы ДФЭ) При многофакторном эксперименте, особенно когда число факторов больше шести (n > 6), число опытов планов ПФЭ 2n (N = 2n) становится чрезмерным. Если нам не требуется определение всех коэффициентов неполного квадратичного полинома, то переходят к дробному факторному эксперименту (ДФЭ) – части полного факторного эксперимента. Так, например, если требуется определить лишь коэффициенты при самих факторах , то план ПФЭ 2n дает избыточную информацию. Так при , в этом случае требуется определить коэффициентов, тогда как по плану ПФЭ необходимо провести N = 26 =64 опыта. Хотя эта избыточная информация не является бесполезной, она позволяет более точно определить коэффициенты, но все же часто используют планы ДФЭ 2n-k , где k – показатель дробности плана ПФЭ. При k = 1 число опытов в плане ДФЭ в два раза меньше, чем в плане ПФЭ, поэтому такие планы называют полуреплика плана ПФЭ. Так при k=1 для плана ДФЭ 26-1 N =26-1 = 32, при k=2 для плана ДФЭ 26-2 N =26-2 = 16 и такой план называют четвертьрепликой, при k=3 для плана ДФЭ 26-3 N =26-3 = 8. При выборе дробности плана k необходимо учитывать, что число опытов должно быть больше числа членов уравнения. В рассматриваемом случае величина k должна быть такой, чтобы удовлетворялось условие . План ДФЭ строится, как и для плана ПФЭ, но с меньшим числом факторов. Оставшиеся факторы варьируются не произвольно, а так чтобы сохранялась ортогональность плана. Это обеспечивается, если оставшиеся факторы варьируются по выбранному генерирующему соотношению, например, как произведение каких-либо факторов из первой группы. Но это приводит к тому, что в матрице Х будут существовать одинаковые столбцы. Следовательно, мы не сможем найти в чистом виде все коэффициенты неполного квадратичного полинома, а лишь определим совместную величину коэффициентов для одинаковых столбцов. Рассмотрим построение плана ДФЭ 23-1. Здесь n = 3, к =1, N=23-1=4. Первые два фактора варьируем как и ранее для плана ПФЭ 22, а для третьего фактора выбираем генерирующее соотношение в виде . Для неполного квадратичного полинома количество столбцов плана составляет восемь. 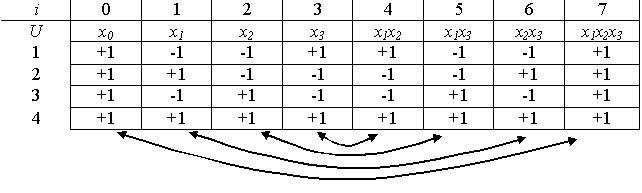  План является ортогональным, но в нем оказались четыре пары одинаковых столбцов. Поэтому можно определить только четыре коэффициента, отражающие совместные влияния двух одинаковых столбцов . Суммарные значения коэффициентов ; ; определяются аналогично. Это следствие того, что мы пытаемся определить полное количество коэффициентов – 8 по недостаточному числу опытов - 4. Однако, если заранее известно, что некоторые из членов уравнения равны нулю (пренебрежимо малы) или имеется априорная информация о величинах некоторых коэффициентов, то полученные коэффициенты могут быть вычленены. Так если , то . Если можно допустить, что коэффициенты из их смешанной оценки сопоставимы, то для рассмотренного плана . Графическое изображение планов ПФЭ 23 и ДФЭ 23-1 в факторном пространстве (для трех факторов - трехмерное пространство) представлено на рисунке 12.2. План ПФЭ 23 представлен кубом с восемью узлами (точками плана), а возможные планы ДФЭ 23-1 – проекциями этого куба на три плоскости. То есть из восьми узлов выбираются четыре (Рисунок 12.2, а). Из куба можно также выбрать четыре точки из восьми, не лежащие в одной плоскости, и сформировать план ДФЭ 23-1 (Рисунок 12.2, б).  Рисунок 12.2 - Графическое изображение планов ПФЭ 23 и ДФЭ 23-1 в факторном пространстве Планы ДФЭ, как и планы ПФЭ, являются рототабельными. Планы ДФЭ могут быть как насыщенными, так и ненасыщенными. Достоинство планов ДФЭ заключается и в том, что если построенный на его основе неполный полином не удовлетворяет требованиям по точности, то план ДФЭ легко достраиваются до плана ПФЭ, без потери информации прежних опытах, с формированием более точного полинома. Пример построения плана ДФЭ. Построить план ДФЭ 24-1 и определить полином  Число факторов – 4. Нужно найти 8 коэффициентов полинома. Выбираем 8 из 16 опытов плана ПФЭ 24 таким образом, чтобы были определены независимые коэффициенты при самих факторах, смешанные коэффициенты при парных сочетаниях факторов и в пренебрежении тройными и четверным сочетаниями факторов и при этом сохранялась ортогональность плана. 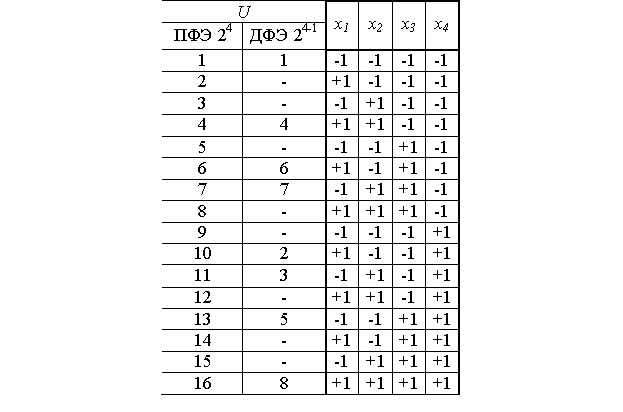 Такой выбор позволяет сформировать план ДФЭ 24-1 как и план ПФЭ 23, но с х4=х1х2х3 . План ДФЭ 24-1 представляется в виде 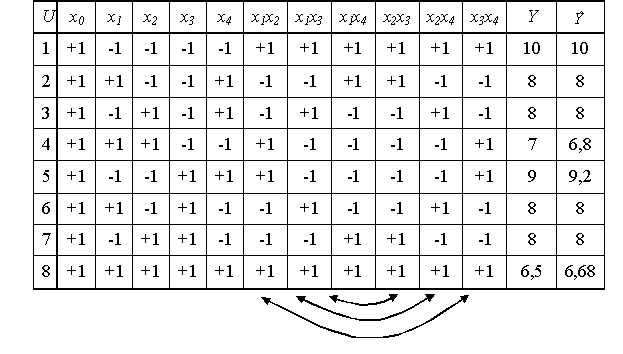 Значения коэффициентов полинома составляют: . ; ;  ;Если принять, что , , , то полином имеет вид  .Значения полинома в точках плана приведены в последнем столбце плана ДФЭ 24-1. В нашем случае точность его достаточно высокая. Основная литература Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с. Исмаилов С.У. Современные методы идентификации объектов и систем управления. Методические указания к выполнению лабораторных работ для магистрантов спец. 6М0702. Шымкент, ЮКГУ, 2010 г., -78 с. Лекция 13 Методы планирования эксперимента (часть 3)Ортогональное планирования эксперимента Другое название - планы Бокса-Уилсона. Для построения ортогональных центральных композиционных планов (ЦКП) используется так называемое звездное плечо α (плечо звездных точек). Это опыты, которые проводятся дополнительно, например, к плану ПФЭ (при k<5) или к дробному плану(при k≥5). В таблице 13.1. приведено такое дополнение к плану в таблице 13.2. Таблица 13.1 Дополнение к плану ПФЭ
Общее количество опытов определяется по формуле:  (при k<5) (13.1)Обычно звездные точки и точку в центре добавляют, если при ПФЭ не удается получить адекватную математическую модель и при исследовании области, близкой к экстремуму. При описании такой области наиболее широко используют полиномы второго порядка. ЦКП неортогональны, но легко сводятся к ортогональным (ОЦКП), путем выбора α. Значения α приведены в таблице 13.2. ([1]., стр.181, 183) Таблица 13.2
Матрица планирования для ОЦКП, используемая для расчета коэффициентов дополняется столбцами  ,  …Например при k=2 и N0=1 получаем матрицу, приведенную в таблице 13.3. В таблице , введено для получения ортогональной матрицы.Таблица 13.3
Благодаря ортогональности матрицы планирования все коэффициенты рассчитываются независимо друг от друга по формуле: 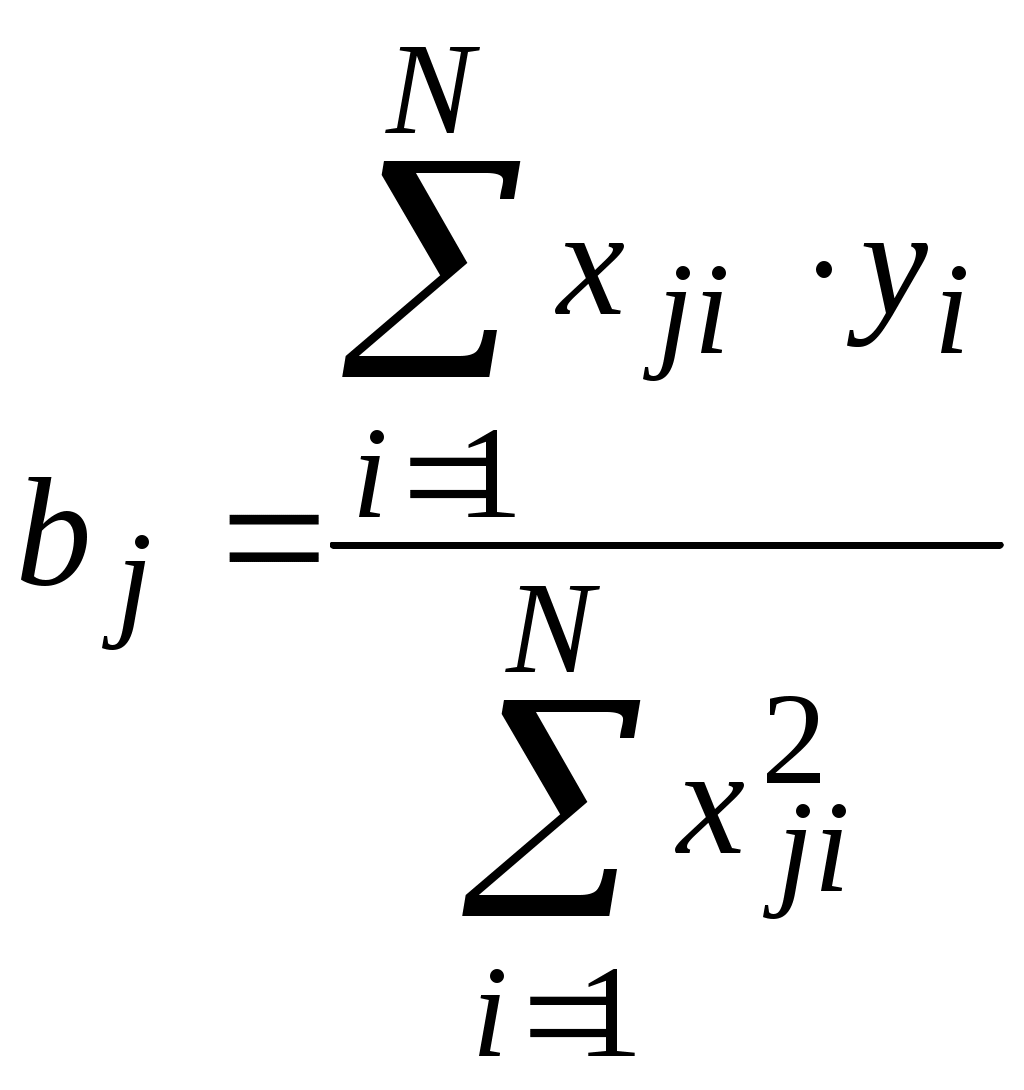 , (13.2) ,а дисперсии коэффициентов равны: 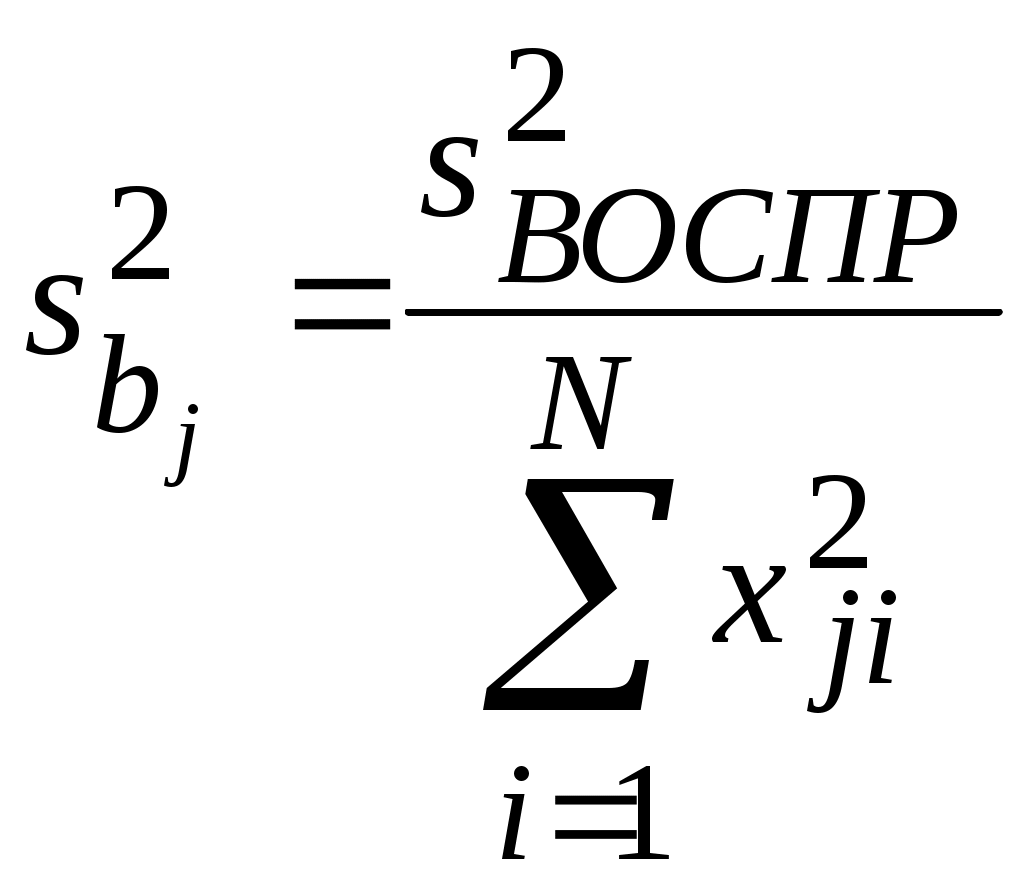 (13.3) В результате расчета по матрице в таблице 13.3 уравнение регрессии в ОЦКП получается в виде:  Чтобы перейти к обычной записи  определяют по выражению: и оценивают с дисперсией:  Зная дисперсию воспроизводимости, проверяют значимость коэффициентов и адекватность уравнения регрессии:  Адекватность проверяют по критерию Фишера, составляя отношение дисперсий: 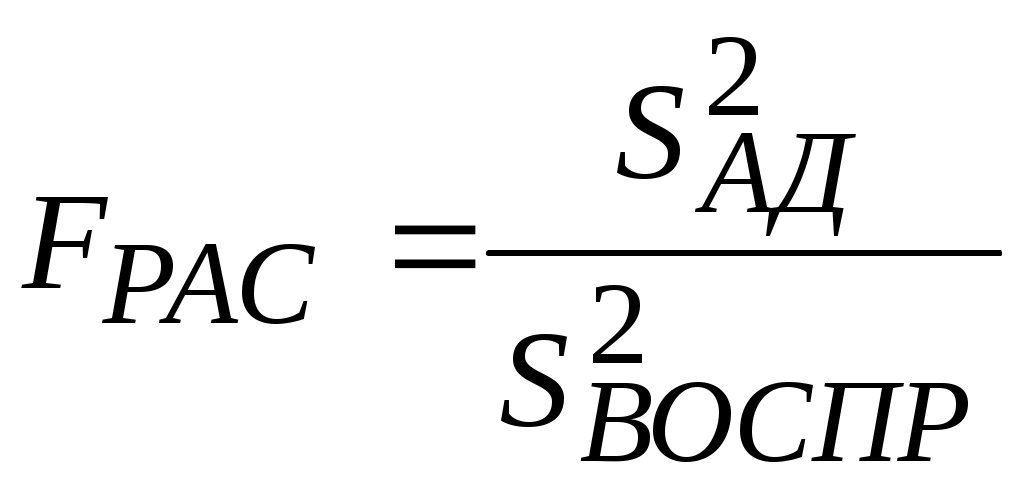 , условие адекватности  , где   . Значимость коэффициентов определяют по формуле:  , если  >  , то  считается значимым.Т.к. в ОЦКП определяются с разной точностью, то (при k<5): ,   Подведем итог. Рототабельные планы – это планы, у которых точки плана располагаются на окружностях (сферах, гиперсферах). У рототабельного плана первого порядка точки плана располагаются на одной окружности (сфере, гиперсфере) с радиусом R , где V=1,…, N - номер точки плана, i =1,…, n – номер фактора. В таком случае точность оценивания функции отклика по любому направлению факторного пространства (для всех точек плана) одинаковая. Рототабельный план может быть симметричным, когда точки плана располагаются симметрично друг друга. Рассмотренный ранее план ПФЭ 2n – рототабельный симметричный план первого порядка. У рототабельных планов второго порядка точки плана располагаются на двух концентрических гиперсферах с радиусами R1 и R2 . В таких планах , для V =1,…, N0 и , для W=1,…, n0, где V и W – текущие номера точек плана в двух подмножествах опытов N0 и n0 из их общего количества N, относящихся к двум разным концентрическим сферам. Одна из сфер может быть вырожденной, когда R2=0. Рассмотренный ранее ортогональный центрально-композиционный план второго порядка (ОЦКП) не является рототабельным планом, так как его точки лежат на трех концентрических окружностях (сферах, гиперсферах). При n=2 это очевидно из Рисунок 14. “Звездные” точки плана и точки плана ПФЭ 2n лежат на разных окружностях. 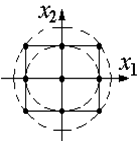 Рисунок 13.1 -. Расположение точек ОЦКП на трех окружностях Рототабельный план может быть ортогональным, если выполняется условие , где , , , - номера столбцов плана. Лекция 14 Методы планирования эксперимента (часть 4)Рототабельное планирования эксперимента. Рототабельный ортогональный центрально-композиционный план (РОЦКП) строится аналогично рассмотренному ранее ОЦКП. К использованному в качестве ядра плану ПФЭ 2n добавляются “звездные” точки - по две на каждый фактор и несколько точек в центре плана. “Звездные” точки должны располагаться на поверхности гиперсферы с радиусом R, на которой лежат и точки плана ПФЭ 2n, то есть величина плеча “звездных” точек должна равняться радиусу R. Это может быть обеспечено, при выполнении условия ортогональности, только при соответствующем выборе числа наблюдений в центральной (нулевой) точке плана n0. Для РОЦКП n0 зависит от числа факторов n. Напомним, что в ОЦКП n0 = 1 для любого числа n. Радиус сферы, на которой лежат точки плана ПФЭ 2n при двух уровнях варьирования факторов с диапазоном 1 составляет (Рисунок 13.2) 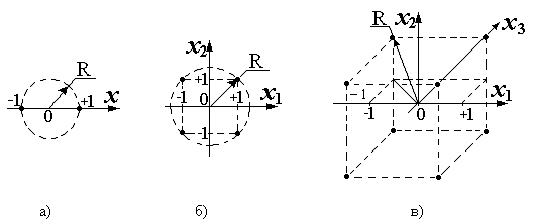 Рисунок 13.2 -. Радиус окружности (сферы), на которой лежат точки плана ПФЭ 2n при диапазоне варьирования факторов от –1 до +1: а) - n=1, ; б) - n=2, ; в) - n=3, . Таким образом, при построении РОЦКП с ядром из плана ПФЭ 2n плечо “звездных” точек определяется числом факторов . Раннее при определении параметров ортогонального композиционного плана второго порядка с ядром из плана ПФЭ 2n было получено , где - число точек плана ПФЭ, - полное число точек композиционного плана второго порядка, - константа преобразования элементов столбцов, соответствующих квадратам факторов. В этом случае для РОЦКП число наблюдений в центре плана . Если n0 не целое, то при практическом построении плана его округляют до целого, но свойство ортогональности плана нарушается. Параметры РОЦКП в зависимости от числа факторов 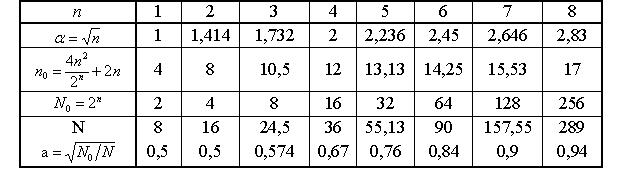 В [1] без вывода для РОЦКП рекомендуется принимать . Тогда . Параметры РОЦКП по [1] 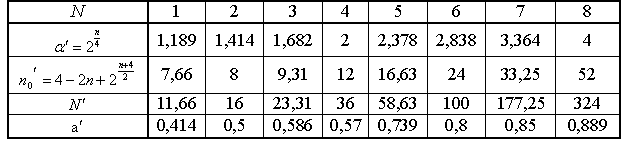 Пример рототабельного ортогонального центрально-композиционного плана для n = 2. Параметры плана: 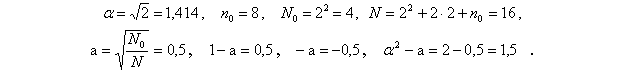 Нет необходимости проводить восемь раз (точки с 9 по 16) опыты в центре плана. Достаточно провести этот опыт один раз и записать результат во все восемь строк. Строки сокращать нельзя, так как нарушается свойство ортогональности, и коэффициенты полинома будут определены неверно. Коэффициенты квадратичного полинома рассчитаются, как и ранее. Использован рассмотренный ранее план ПФЭ 22 с добавленными опытами 5-16. Основная литература Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с. Исмаилов С.У. Современные методы идентификации объектов и систем управления. Методические указания к выполнению лабораторных работ для магистрантов спец. 6М0702. Шымкент, ЮКГУ, 2010 г., -78 с. Дополнительная литература Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с. Лекция 15 Методы планирования эксперимента (часть 5)Эволюционное планирование эксперимента Планирование эксперимента (англ. experimental design techniques) — комплекс мероприятий, направленных на эффективную постановку опытов. Основная цель планирования эксперимента – достижение максимальной точности измерений при минимальном количестве проведенных опытов и сохранении статистической достоверности результатов. Планирование эксперимента применяется при поиске оптимальных условий, построении интерполяционных формул, выборе значимых факторов, оценке и уточнении констант теоретических моделей и др. История Планирование эксперимента возникло в 20-х годах XX века из потребности устранить или хотя бы уменьшить систематические ошибки в сельскохозяйственных исследованиях путем рандомизации условий проведения эксперимента. Процедура планирования оказалась направленной не только на уменьшение дисперсии оцениваемых параметров, но также и на рандомизацию относительно сопутствующих, спонтанно изменяющихся и неконтролируемых переменных. В результате удалось избавится от смещения в оценках. С 1918 г. Р. Фишер начал свою известную серию работ на Рочемстедской агробиологической станции в Англии. В 1935 году появилась его монография «Design of Experiments», давшая название всему направлению. В 1942 году А. Кишен рассмотрел планирование эксперимента по латинским кубам, которое явилось дальнейшим развитием теории латинских квадратов. Затем Р. Фишер независимо опубликовал сведения об ортогональных гипер-греко-латинских кубах и гипер-кубах. Вскоре после этого в 1946 г. Р. Рао рассмотрел их комбинаторные свойства. Дальнейшему развитию теории латинских квадратов посвящены работы Х. Манна (1947 – 1950 гг.). Первое глубокое математическое исследование блок-схемы выполнено Р. Боузом в 1939 г. Вначале была разработана теория сбалансированных неполноблочных планов (BIB-схемы). Затем Р. Боуз, К. Нер и Р. Рао обобщили эти планы и разработали теорию частично сбалансированных неполноблочных планов (РBIB-схемы). С тех пор изучению блок-схем уделяется большое внимание как со стороны специалистов по планированию эксперимента (Ф. Йетс, Г. Кокс, В. Кохрен, В. Федерер, К. Гульден, О. Кемптгорн и другие), так и со стороны специалистов по комбинаторному анализу (Боуз, Ф. Шимамото, В. Клатсворси, С. Шрикханде, А. Гофман и др.). Исследования Р. Фишера знаменуют начало первого этапа развития методов планирования эксперимента. Фишер разработал метод факторного планирования. Йетс предложил для этого метода простую вычислительную схему. Факторное планирование получило широкое распространение. Особенностью факторного эксперимента является необходимость ставить сразу большое число опытов. В 1945 г. Д. Финни ввел дробные реплики от факторного эксперимента. Это позволило сократить число опытов и открыло дорогу техническим приложениям планирования. Другая возможность сокращения необходимого числа опытов была показана в 1946 г. Р. Плакеттом и Д. Берманом, которые ввели насыщенные факторные планы. Г. Хотеллинг в 1941 г. предложил находить экстремум по экспериментальным данным с использованием степенных разложений и градиента. Следующим важным этапом было введение принципа последовательного шагового экспериментирования. Этот принцип, высказанный в 1947 г. М. Фридманом и Л. Сэвиджем, позволил распространить на экспериментальное определение экстремума – итерацию. Чтобы построить современную теорию планирования эксперимента, не хватало одного звена – формализации объекта исследования. Это звено появилось в 1947 г. после создания Н. Винером теории кибернетики. Кибернетическое понятие «черный ящик», играет в планировании важную роль. В 1951 г. работой американских ученых Дж. Бокса и К. Уилсона начался новый этап развития планирования эксперимента. В ней сформулирована и доведена до практических рекомендаций идея последовательного экспериментального определения оптимальных условий проведения процессов с использованием оценки коэффициентов степенных разложений методом наименьших квадратов, движение по градиенту и отыскание интерполяционного полинома в области экстремума функции отклика (почти стационарной области). В 1954 – 1955 гг. Лж. Бокс, а затем П. Юл. показали, что планирование эксперимента можно использовать при исследовании физико-химических процессов, если априори высказаны одна или несколько возможных гипотез. Направление получило развитие в работах Н. П. Клепикова, С. Н. Соколова и В. В. Федорова в ядерной физике. Третий этап развития теории планирования эксперимента начался в 1957 г., когда Бокс применил свой метод в промышленности. Этот метод стал называться «эволюционным планированием». В 1958 г. Г. Шиффе предложил новый метод планирования эксперимента для изучения физико-химических диаграмм состав – свойство под названием «симплексной решетки». Развитие теории планирование эксперимента в СССР отражено в работах В. В. Налимова, Ю. П. Адлера, Ю. В. Грановского, Е. В. Марковой. Особенности планирования эксперимента в производственных условиях При переходе от лабораторных условий к промышленным результатам исследований довольно часто плохо воспроизводятся в основном из-за резко увеличивающегося числа случайных факторов. Поэтому приходится продолжать эксперименты и при промышленном производстве продукции. С целью уменьшения доли выпуска бракованной продукции при промышленных экспериментах применяют небольшие интервалы варьирования факторов по сравнению с лабораторными исследованиями. Планы промышленных экспериментов составляют таким образом, чтобы путем осторожного изменения факторов получить информацию об изменениях отклика объекта и при этом выпустить качественную продукцию. Такой подход к планированию промышленных экспериментов был предложен Боксом и получил название "Метод эволюционного планирования эксперимента". Эволюционное планирование (ЭВОП). Метод экспериментальной оптимизации, сочетающий многократное использование дробных и полных факторных планов с движением по градиенту функции отклика и предназначенный для совершенствования производственных объектов Существуют различные модификации ЭВОП: обычное ЭВОП (ЭВОП Бокса), последовательный симплексный метод, квадратичное вращаемое ЭВОП и т. п. Основная литература Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с. Исмаилов С.У. Современные методы идентификации объектов и систем управления. Методические указания к выполнению лабораторных работ для магистрантов спец. 6М0702. Шымкент, ЮКГУ, 2010 г., -78 с. Дополнительная литература Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с. Гроп Д. Методы идентификации систем. - М.: Мир, 1979 Модуль 2. Моделирование и идентификация динамических характеристик объектов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
