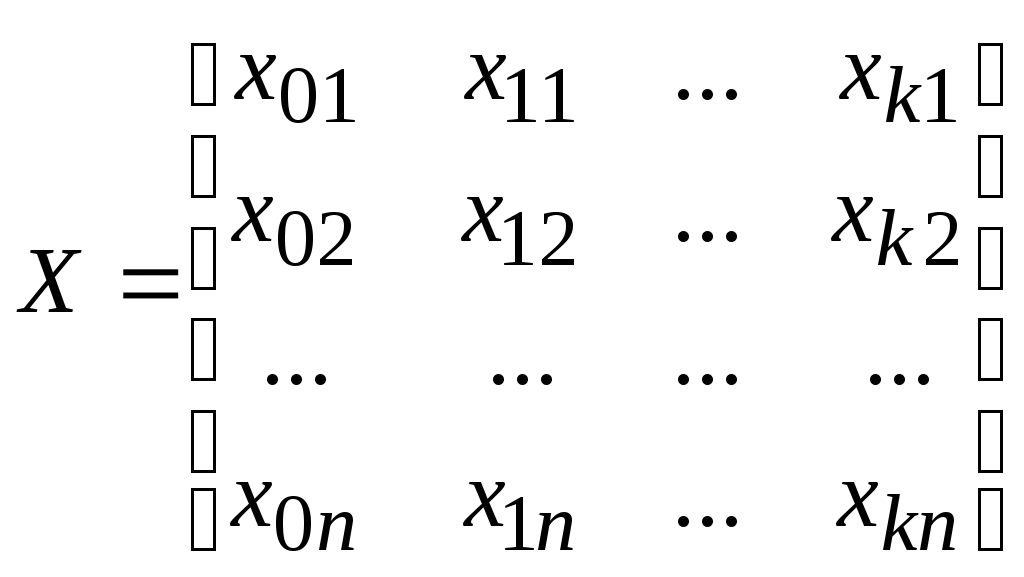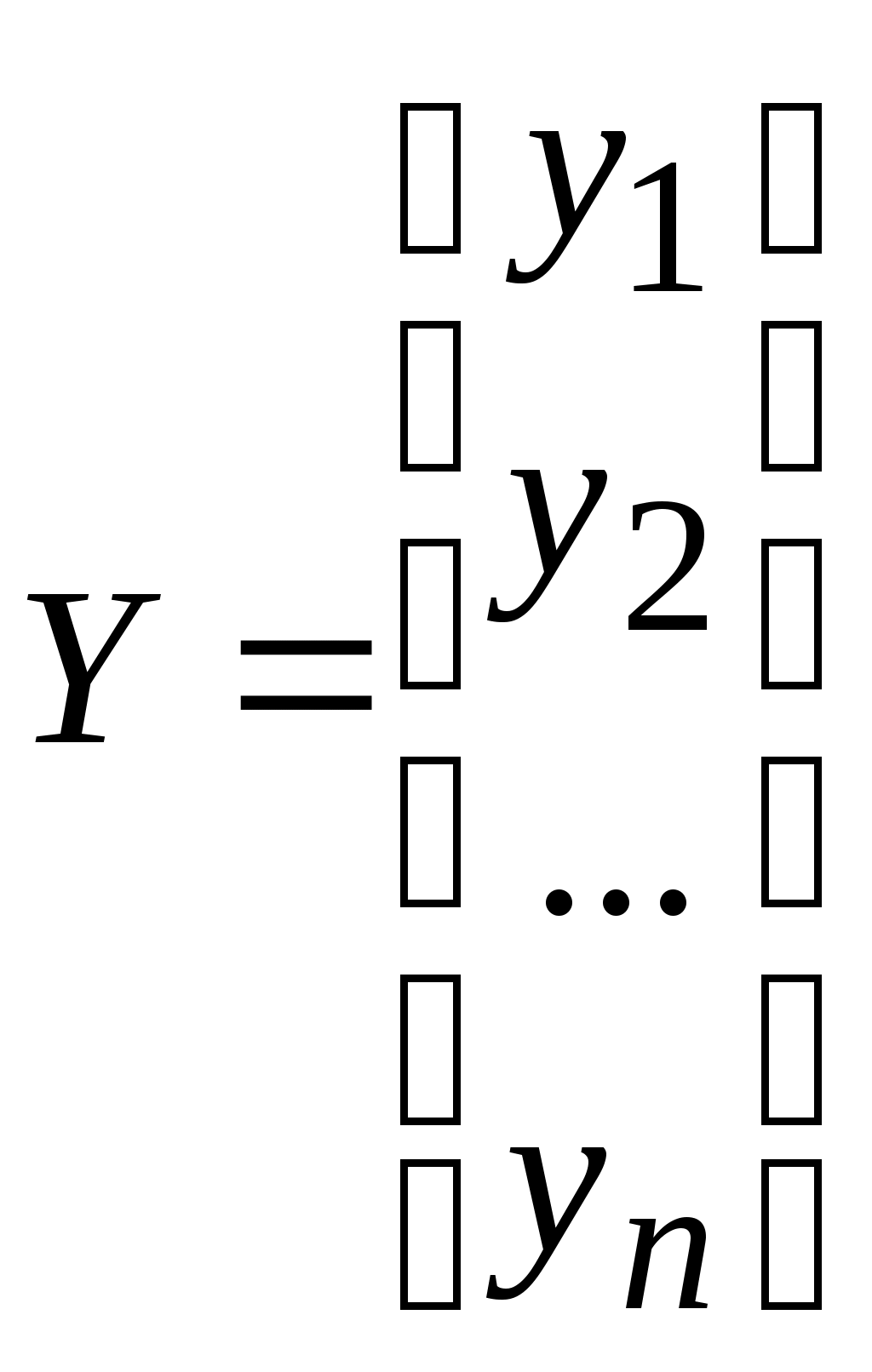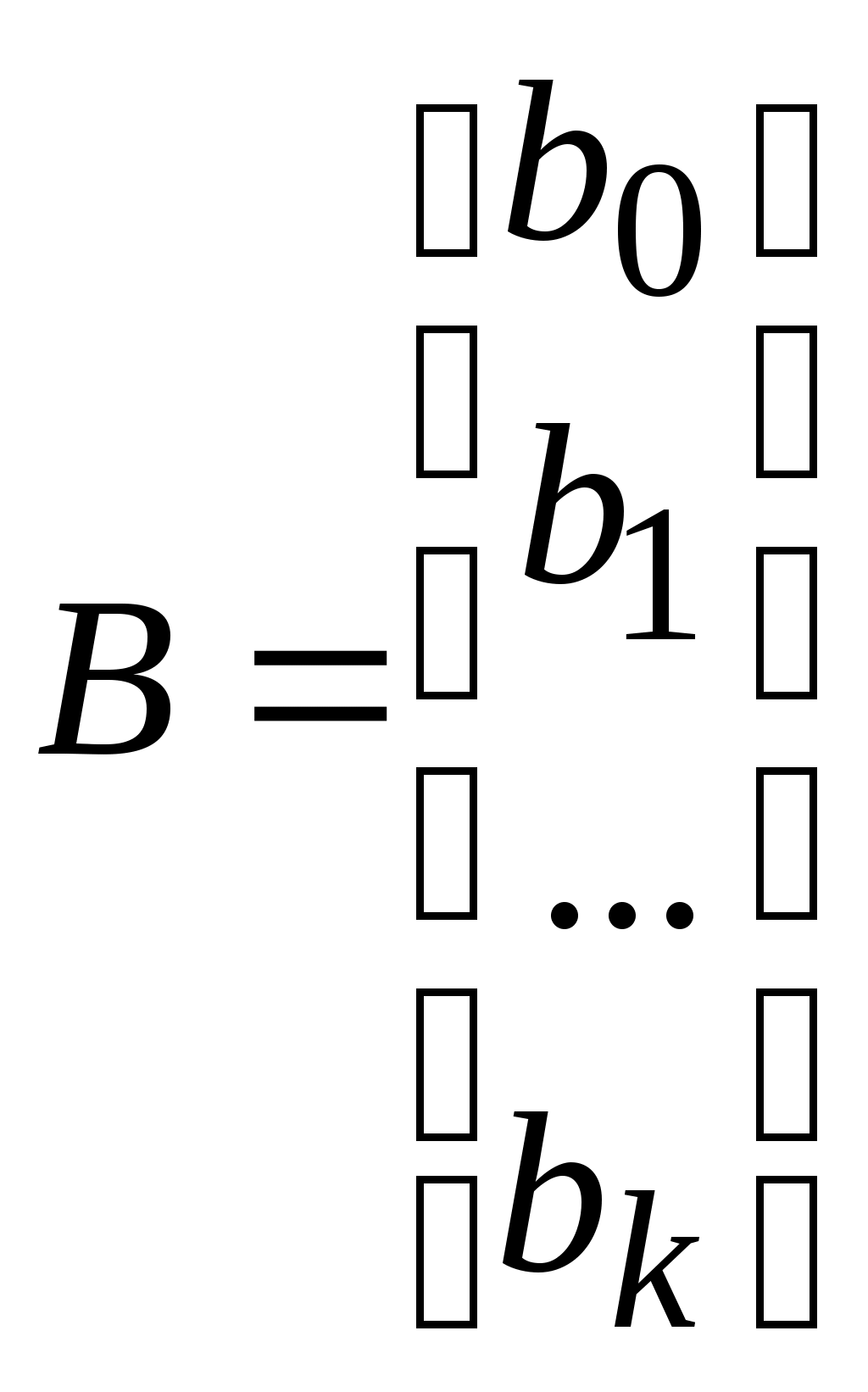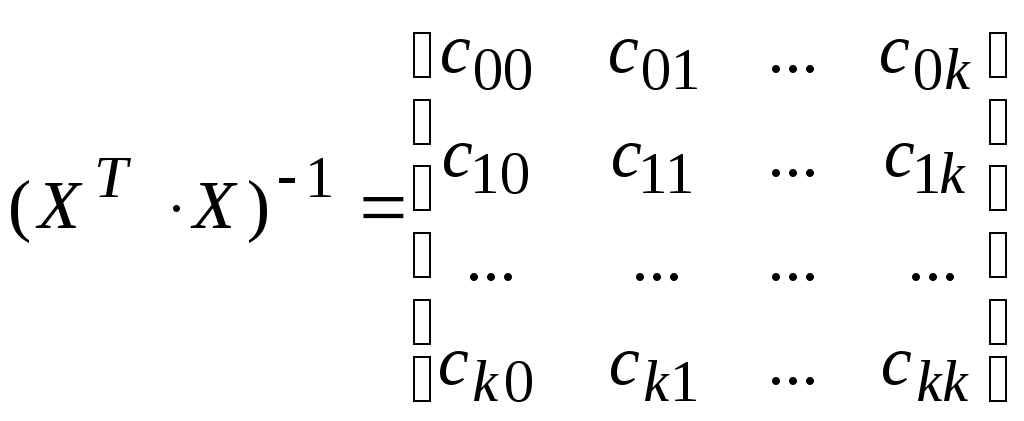Лекция 10 Статические модели в форме управления регрессии и методы их определения (часть 4)
Регрессионный анализ в матричной форме. (См.[1] стр.146)
Использование матричной формы записи значительно упрощает как запись, так и решение задачи определения коэффициентов уравнения регрессии. Введем следующие обозначения (см. таблицу 10.1).
1). Матрица независимых переменных X – она содержит исходный статистический материал (см. таблицу в предыдущей теме, кроме последнего столбца) в ней n – строк и k+1 столбец:
2). Матрица (вектор) наблюдений Y (вектор – столбец): в нем n – строк.
X и Y известны в результате проведенного пассивного эксперимента.
Матрица (вектор) искомых коэффициентов уравнения регрессии B (вектор – столбец): в нем k+1 – строк.
Целью является определение вектора B по известным X и Y по формуле (10.2).
Таблица 10.1
Элементы матричной записи при регрессионном анализе
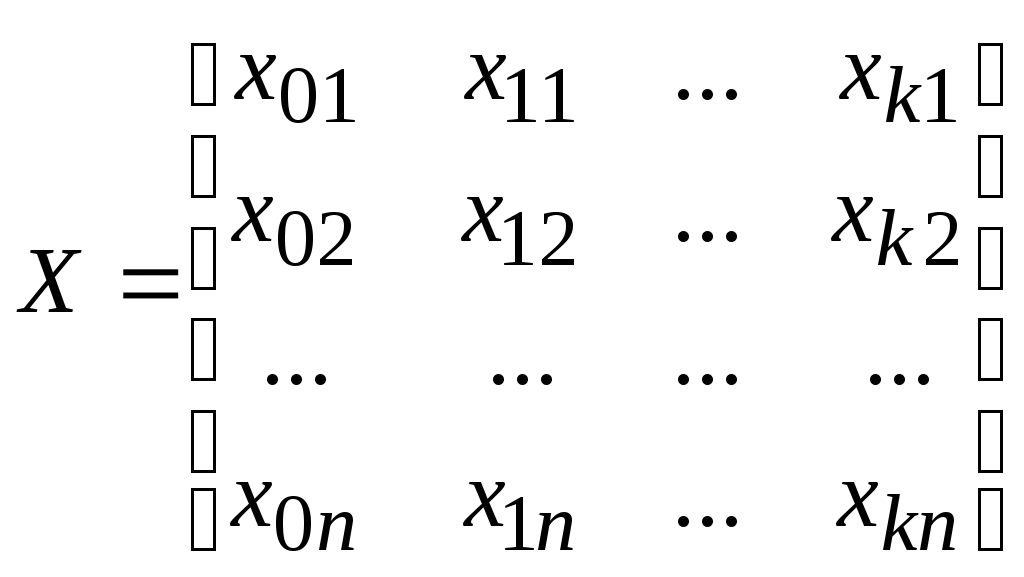
|
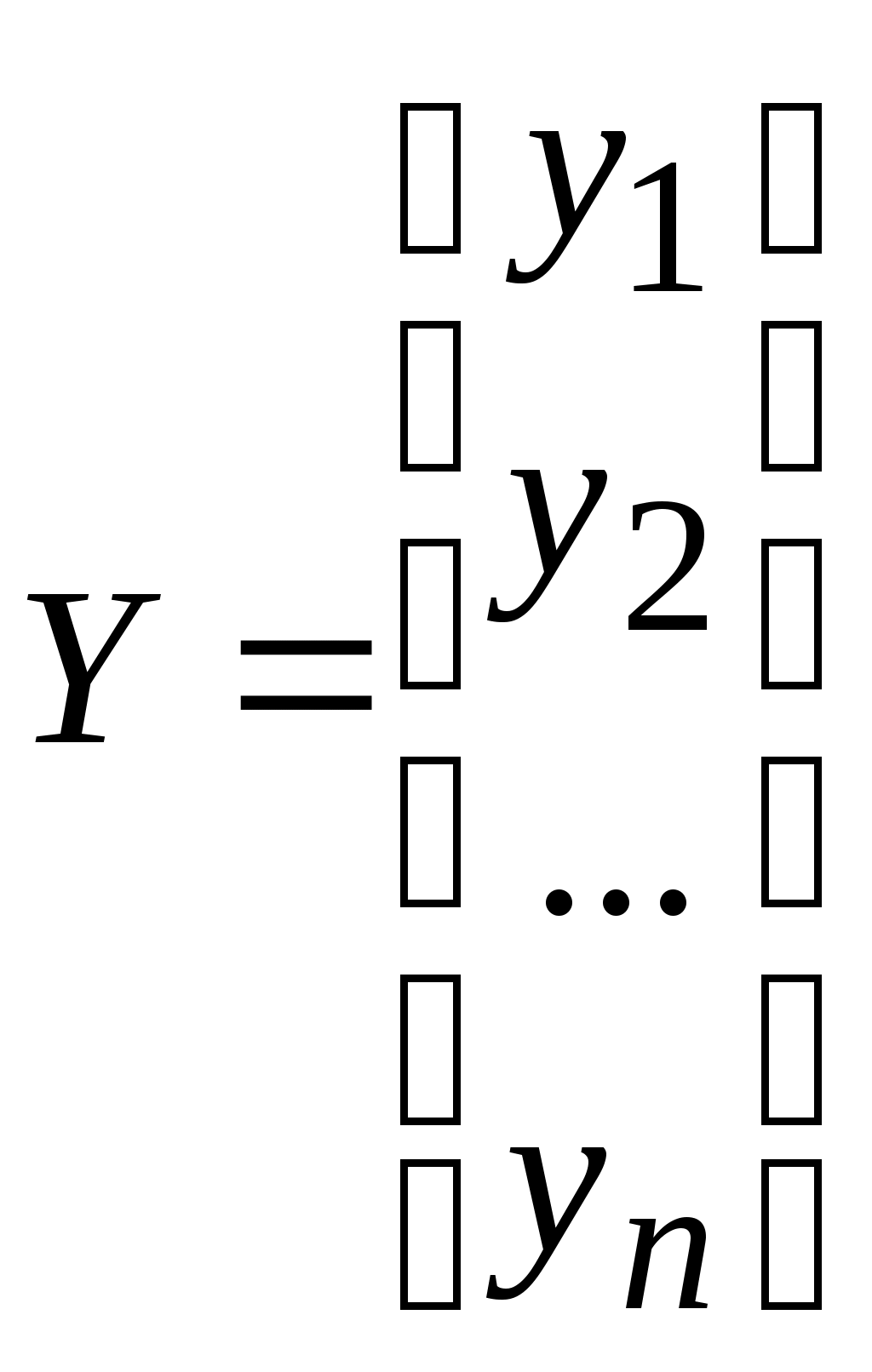
|
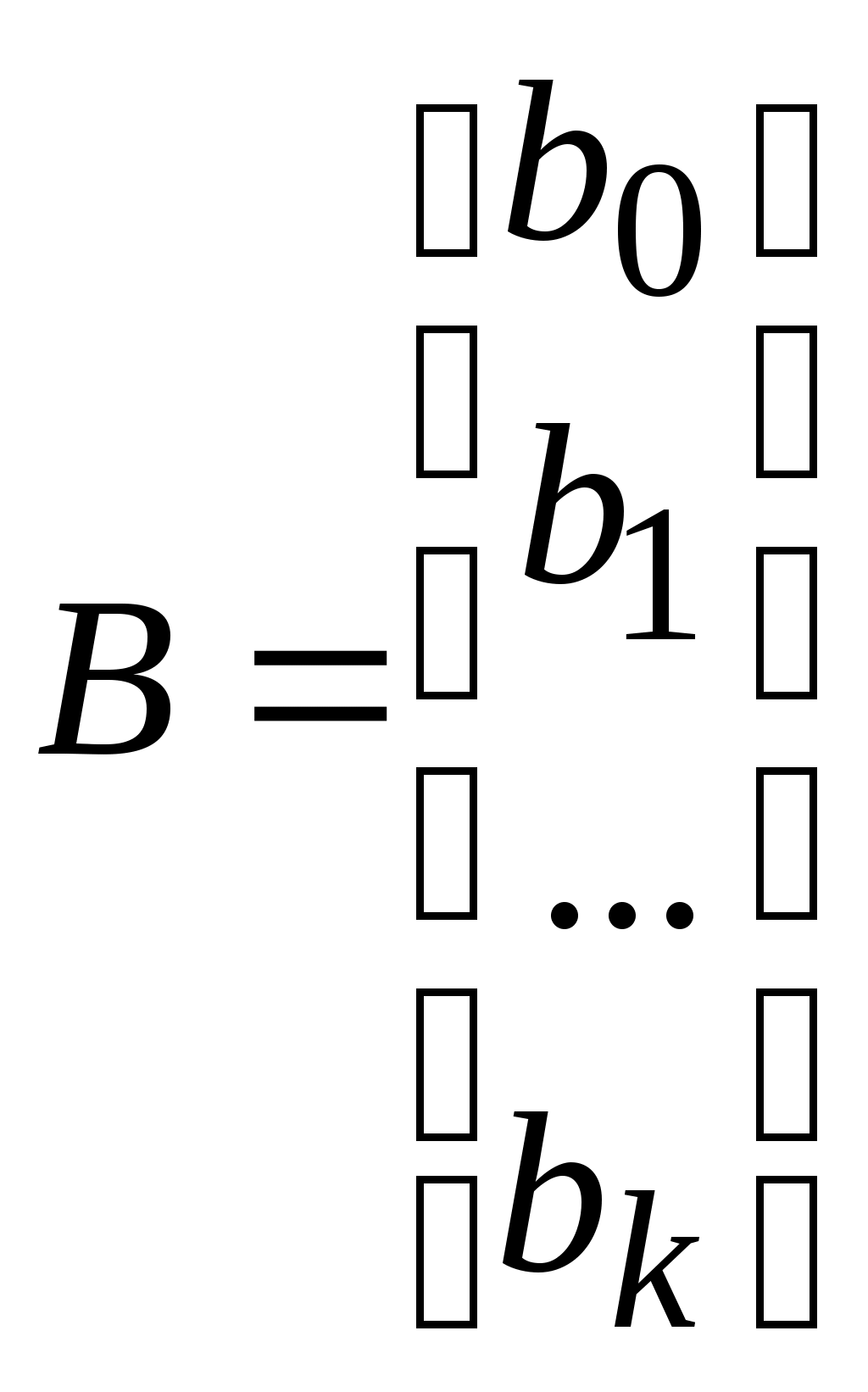
|
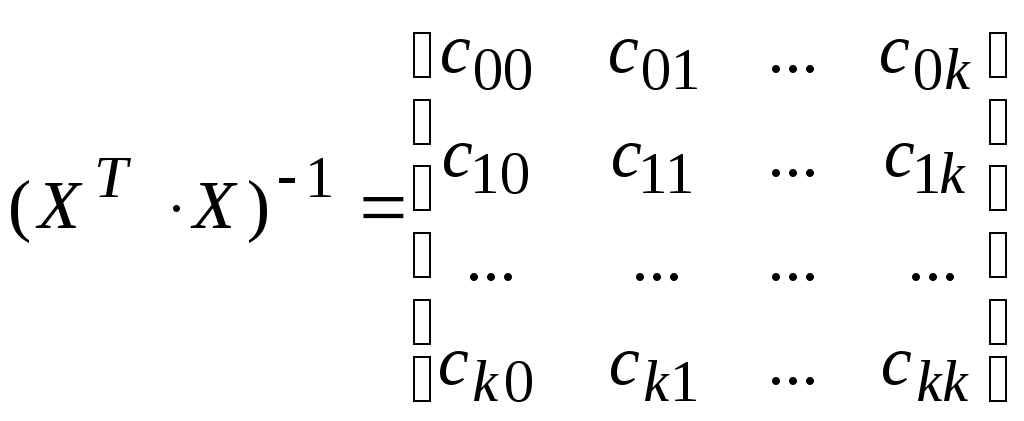
|
Матрица входов – факторы, независимые параметры
|
Вектор выходов (наблюдений)
|
Вектор коэффициентов
|
Ковариационная матрица, матрица ошибок
|
Матрицу 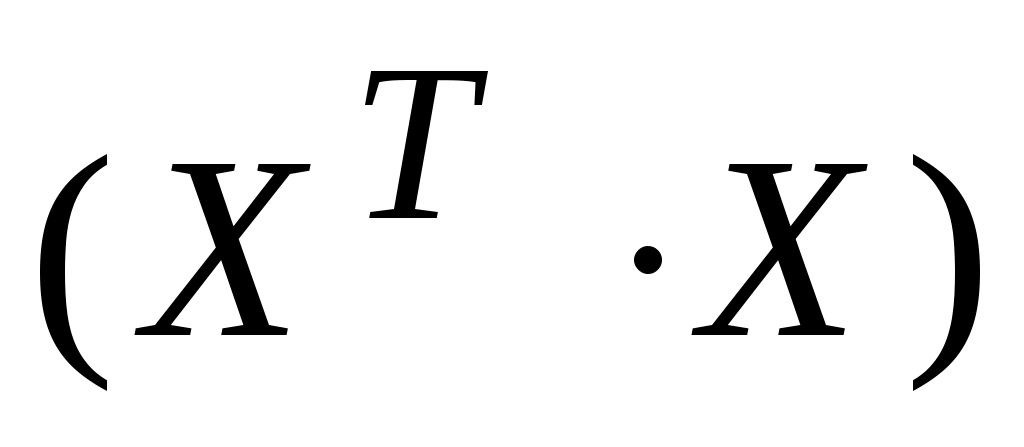 называют информационной матрицей (матрицей моментов), а называют информационной матрицей (матрицей моментов), а 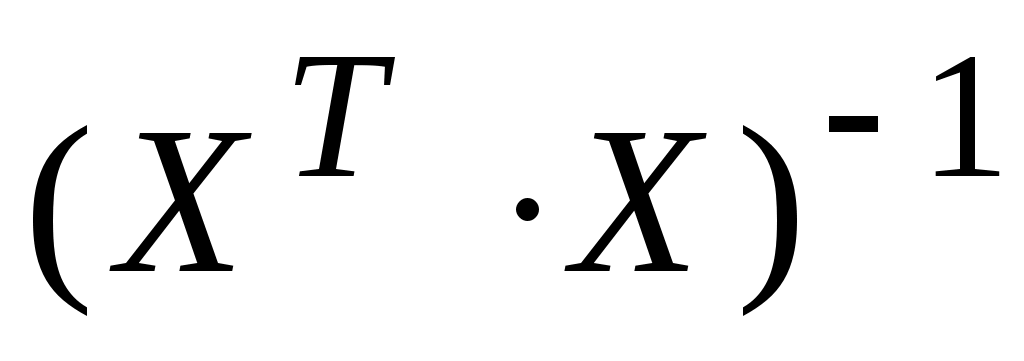 матрицей ошибок или ковариационной матрицей. матрицей ошибок или ковариационной матрицей.
В матричной форме система нормальных уравнений запишется:
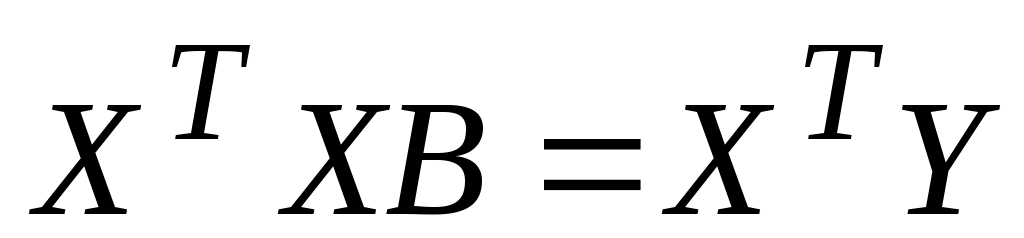 (10.1) (10.1)
Решение этого уравнения имеет вид (хорошо запомните эту формулу!):
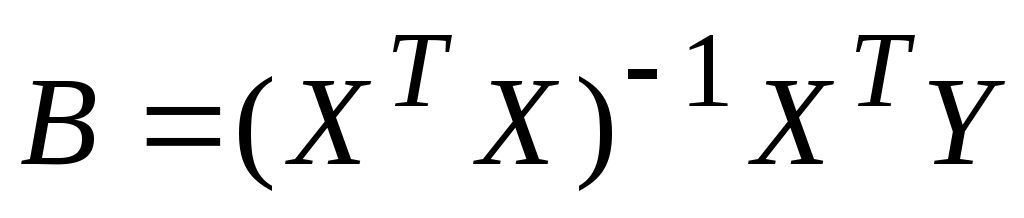 (10.2) (10.2)
Уравнение (4.15) легко реализуется, например, на Mathcad и широко применяется также и в методах планирования эксперимента. Однако вычисление вектора коэффициентов В иногда не может быть вычислено из-за вырожденности матрицы 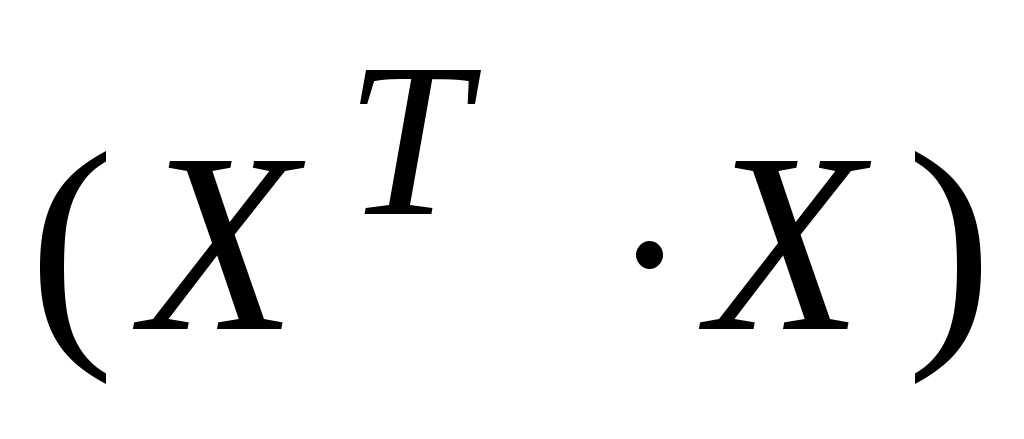 . Это может происходить, например, если элементы матрицы Х очень сильно отличаются друг от друга. Например, когда один из элементов равен 0.00005, в другой 100000.0. . Это может происходить, например, если элементы матрицы Х очень сильно отличаются друг от друга. Например, когда один из элементов равен 0.00005, в другой 100000.0.
Для определения остаточной дисперсии определяют матрицу столбец
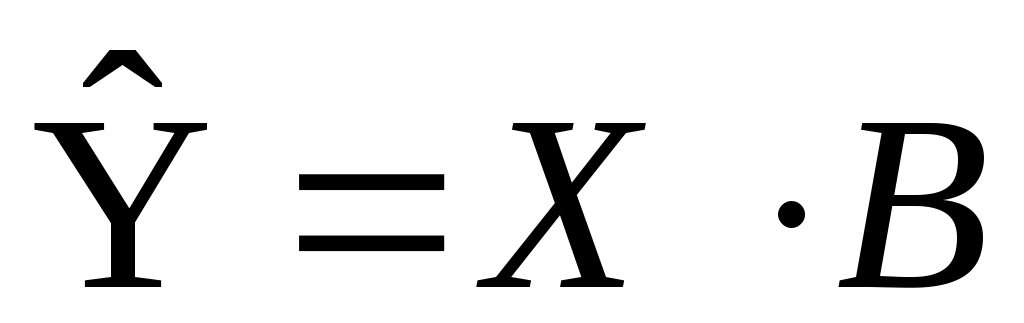 (10.3) (10.3)
Числитель остаточной дисперсии получают по формуле:
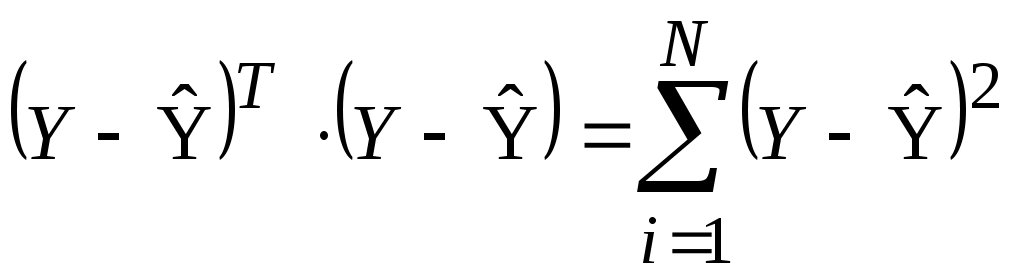 (10.4) (10.4)
Рассмотрим пример применения регрессионного анализа для построения математической модели с тремя входами и одним выходом в виде (10.5):
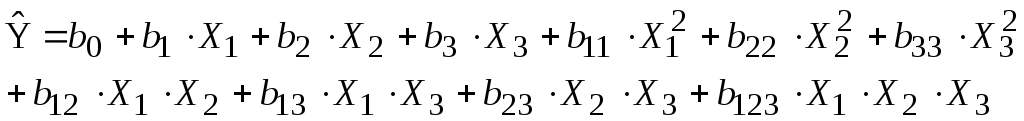 (10.5) (10.5)
Или, что-то же, в виде:
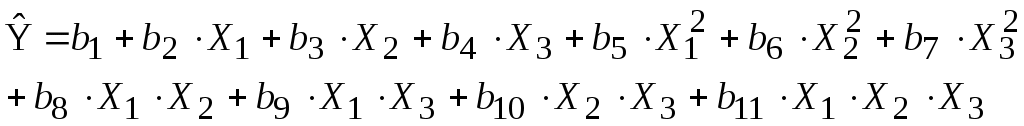 (10.5А) (10.5А)
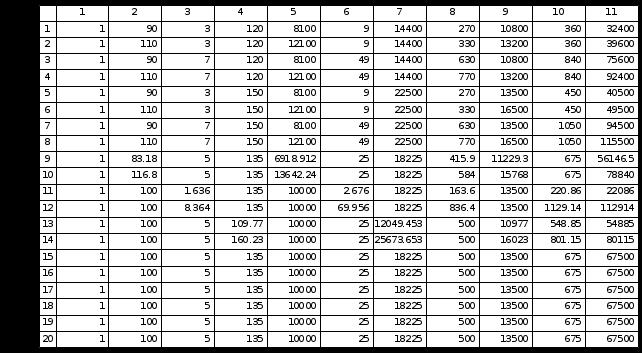
Исходные данные для построения математической модели приведены в таблице 10.2. На основе эксперимента в ней заполнены столбец 2 (значения выхода – Y) и столбцы 4-6 (значения входов Х1, Х2 и Х3). Эти значения выделены в таблице жирным шрифтом.
Столбец 3 заполнен значениями равными 1, а столбцы 7-13 значениями, вычисленными на основе значений столбцов 4-4. Проведено 20 опытов.
Таблица 10.2
Исходные данные для примера построения математической модели
№оп
|
Y-Выход
|
|
Входы - Х
|
Условные входы, рассчитанные на основе входов Х
|
X0
|
X1
|
X2
|
X3
|
X12
|
X22
|
X32
|
X1*X2
|
X1*X3
|
X2*X3
|
X1X2X3
|
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
(6)
|
(7)
|
(8)
|
(9)
|
(10)
|
(11)
|
(12)
|
(13)
|
1
|
43,0
|
1
|
90
|
3
|
120
|
8100
|
9
|
14400
|
270,000
|
10800,000
|
360,000
|
32400
|
2
|
44,0
|
1
|
110
|
3
|
120
|
12100
|
9
|
14400
|
330,000
|
13200,000
|
360,000
|
39600
|
3
|
40,0
|
1
|
90
|
7
|
120
|
8100
|
49
|
14400
|
630,000
|
10800,000
|
840,000
|
75600
|
4
|
38,0
|
1
|
110
|
7
|
120
|
12100
|
49
|
14400
|
770,000
|
13200,000
|
840,000
|
92400
|
5
|
45,0
|
1
|
90
|
3
|
150
|
8100
|
9
|
22500
|
270,000
|
13500,000
|
450,000
|
40500
|
6
|
43,0
|
1
|
110
|
3
|
150
|
12100
|
9
|
22500
|
330,000
|
16500,000
|
450,000
|
49500
|
7
|
44,0
|
1
|
90
|
7
|
150
|
8100
|
49
|
22500
|
630,000
|
13500,000
|
1050,000
|
94500
|
8
|
42,0
|
1
|
110
|
7
|
150
|
12100
|
49
|
22500
|
770,000
|
16500,000
|
1050,000
|
115500
|
9
|
44,0
|
1
|
83,18
|
5,00
|
135,
|
6918,9
|
25
|
18225
|
415,900
|
11229,300
|
675,000
|
56146,5
|
10
|
41,0
|
1
|
116,8
|
5,00
|
135
|
13642
|
25
|
18225
|
584,000
|
15768,000
|
675,000
|
78840
|
11
|
43,0
|
1
|
100
|
1,64
|
135
|
10000
|
2,6766
|
18225
|
163,600
|
13500,000
|
220,860
|
22086
|
12
|
37,0
|
1
|
100
|
8,36
|
135
|
10000
|
69,955
|
18225
|
836,400
|
13500,000
|
1129,140
|
112914
|
13
|
45,0
|
1
|
100
|
5,00
|
109,7
|
10000
|
25
|
12049,45
|
500,000
|
10977,000
|
548,850
|
54885
|
14
|
48,0
|
1
|
100
|
5,00
|
160,3
|
10000
|
25
|
25673,65
|
500,000
|
16023,000
|
801,150
|
80115
|
15
|
47,0
|
1
|
100
|
5
|
135
|
10000
|
25
|
18225
|
500,000
|
13500,000
|
675,000
|
67500
|
16
|
45,0
|
1
|
100
|
5
|
135
|
10000
|
25
|
18225
|
500,000
|
13500,000
|
675,000
|
67500
|
17
|
46,5
|
1
|
100
|
5
|
135
|
10000
|
25
|
18225
|
500,000
|
13500,000
|
675,000
|
67500
|
18
|
45,5
|
1
|
100
|
5
|
135
|
10000
|
25
|
18225
|
500,000
|
13500,000
|
675,000
|
67500
|
19
|
46,7
|
1
|
100
|
5
|
135
|
10000
|
25
|
18225
|
500,000
|
13500,000
|
675,000
|
67500
|
20
|
46,0
|
1
|
100
|
5
|
135
|
10000
|
25
|
18225
|
500,000
|
13500,000
|
675,000
|
67500
|
Таким образом, заданы значения вектора Y (столбец 2) и матрицы X (столбцы 3-13) имеющие значения:
Далее вычислив, например, в системе Mathcad по формуле (10.2) 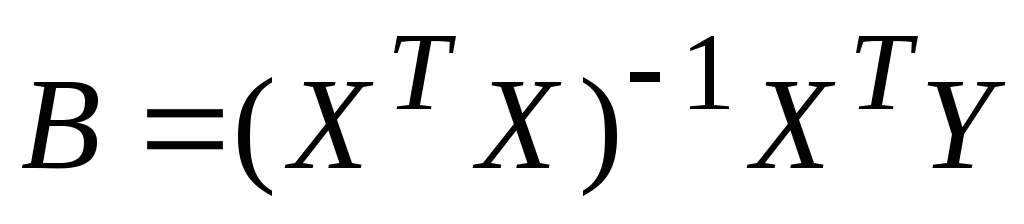 получаем вектор одиннадцати значений коэффициентов В: получаем вектор одиннадцати значений коэффициентов В:

Можно произвести проверку, результаты которой сведены в таблицу 4.3. Расчетное значение выхода  можно получить, применив формулу (10.5А) или её матричный аналог в виде: можно получить, применив формулу (10.5А) или её матричный аналог в виде: 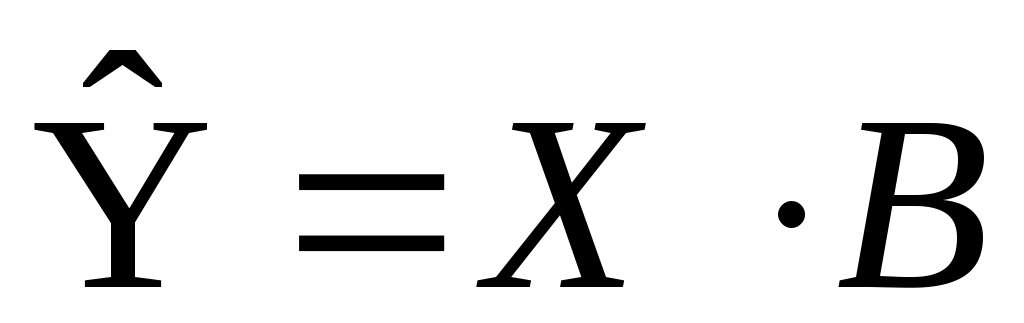 . Полученную нами математическую модель можно считать адекватной, т.к. Значение критерия R2 = 0,9724 достаточно близко к единице. . Полученную нами математическую модель можно считать адекватной, т.к. Значение критерия R2 = 0,9724 достаточно близко к единице.
Таблица 4.1
Результат проверки адекватности математической модели
№ опыта
|
Входные переменные
|
Выход
|
Погрешность (ошибка)
|
X1
|
X2
|
X3
|
Y
|

|
абсолютная
|
относительная %
|
1
|
120,00
|
3,00
|
120,00
|
43,000
|
43,5514
|
-0,5514
|
-1,2823
|
2
|
120,00
|
3,00
|
120,00
|
44,000
|
44,3277
|
-0,3277
|
-0,7448
|
3
|
120,00
|
7,00
|
120,00
|
40,000
|
40,2128
|
-0,2128
|
-0,5321
|
4
|
120,00
|
7,00
|
120,00
|
38,000
|
37,9892
|
0,0108
|
0,0285
|
5
|
150,00
|
3,00
|
150,00
|
45,000
|
45,3582
|
-0,3582
|
-0,7959
|
6
|
150,00
|
3,00
|
150,00
|
43,000
|
43,1345
|
-0,1345
|
-0,3127
|
7
|
150,00
|
7,00
|
150,00
|
44,000
|
44,0196
|
-0,0196
|
-0,0446
|
8
|
150,00
|
7,00
|
150,00
|
42,000
|
41,7959
|
0,2041
|
0,4858
|
9
|
135,00
|
5,00
|
135,00
|
44,000
|
43,4885
|
0,5115
|
1,1625
|
10
|
135,00
|
5,00
|
135,00
|
41,000
|
41,0205
|
-0,0205
|
-0,0499
|
11
|
135,00
|
1,64
|
135,00
|
43,000
|
42,3519
|
0,6481
|
1,5072
|
12
|
135,00
|
8,36
|
135,00
|
37,000
|
37,1570
|
-0,1570
|
-0,4243
|
13
|
109,77
|
5,00
|
109,77
|
45,000
|
44,5247
|
0,4753
|
1,0562
|
14
|
160,23
|
5,00
|
160,23
|
48,000
|
47,9842
|
0,0158
|
0,0329
|
15
|
135,00
|
5,00
|
135,00
|
47,000
|
46,1306
|
0,8694
|
1,8497
|
16
|
135,00
|
5,00
|
135,00
|
45,000
|
46,1306
|
-1,1306
|
-2,5125
|
17
|
135,00
|
5,00
|
135,00
|
46,500
|
46,1306
|
0,3694
|
0,7943
|
18
|
135,00
|
5,00
|
135,00
|
45,500
|
46,1306
|
-0,6306
|
-1,3860
|
19
|
135,00
|
5,00
|
135,00
|
46,700
|
46,1306
|
0,5694
|
1,2192
|
20
|
135,00
|
5,00
|
135,00
|
46,000
|
46,1306
|
-0,1306
|
-0,2840
|
Суммарная ошибка =
|
1,0851E-07
|
-0,2330
|
Среднее значение ошибки =
|
5,4256E-09
|
-0,0117
|
Значение критерия Rквадрат =
|
0,9724
|
Основная литература
Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с.
Построение математических моделей химико-технологических процессов. Под ред. Дудникова Е.Г. - Л.: Химия, 1970. –312 с.
Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с.
Дополнительная литература
Толчеев В.О., Ягодкина Т.В. Методы идентификации линейных одномерных динамических систем. -М.: Изд-во МЭИ, 1997
|
 Скачать 4.07 Mb.
Скачать 4.07 Mb.