Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление

• Название: Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
• Дата: 24.01.2023
• Размер: 4.07 Mb.
• Имя файла: Лекц комплекс СМИОСУ 2017.doc
• Тип: Конспект лекций; #902228
• страница: 6 из 29

Лекция 5 Оценка статистических показателей(часть1)

Математическое ожидание и дисперсия, их оценка и свойства

Математическое ожидание — мера среднего значения случайной величины в теории вероятностей. В зарубежной литературе обозначается через (например, от англ. Expected value или нем. Erwartungswert), в русской M[X] (возможно, от англ. Mean value, а возможно от русск. Математическое ожидание). В статистике часто используют обозначение μ.

Определение. Пусть задано вероятностное пространство 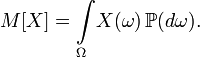и определённая на нём случайная величина X. То есть, по определению,  — измеримая функция. Тогда, если существует интеграл Лебега от X по пространству Ω, то он называется математическим ожиданием, или средним значением и обозначается M[X] или .



Основные формулы для математического ожидания

Если FX(x) — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса: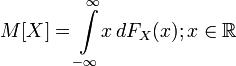

.

Дисперсия случайной величины— мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается D[X] в русской литературе и (англ. variance) в зарубежной. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии, равный , называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.

Из неравенства Чебышёва следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/k². Так, например, как минимум в 75% случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89% — не более чем на три.

Определение. Пусть — случайная величина, определённая на некотором вероятностном пространстве. Тогда

где символ M обозначает математическое ожидание.
В инженерной практине используется понятие оценка, оно обычно означает, что вычисление производится на конечном интервазк выборки.

Оценка математического ожидания переменной Х (обозначается mX или ):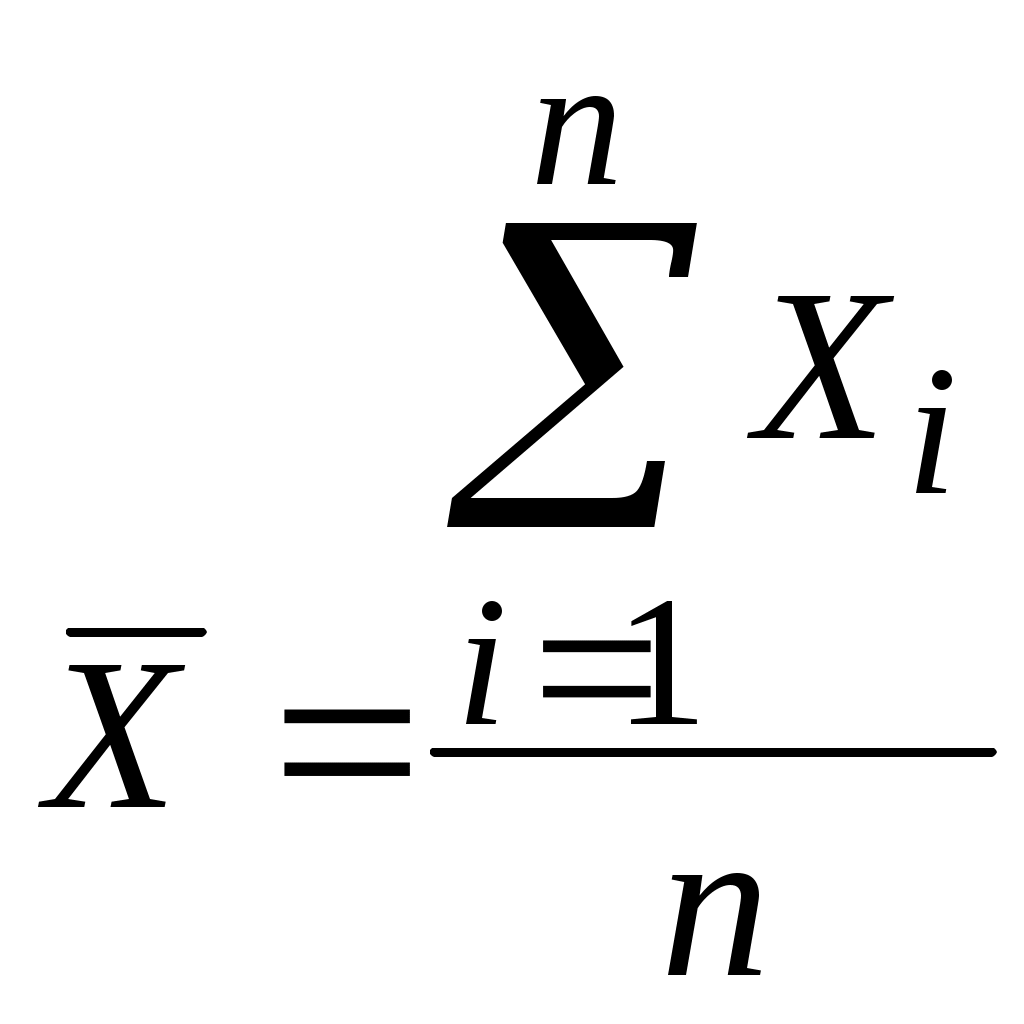

(5.1)

n – количество опытов

Оценка дисперсии переменной Х (обозначается 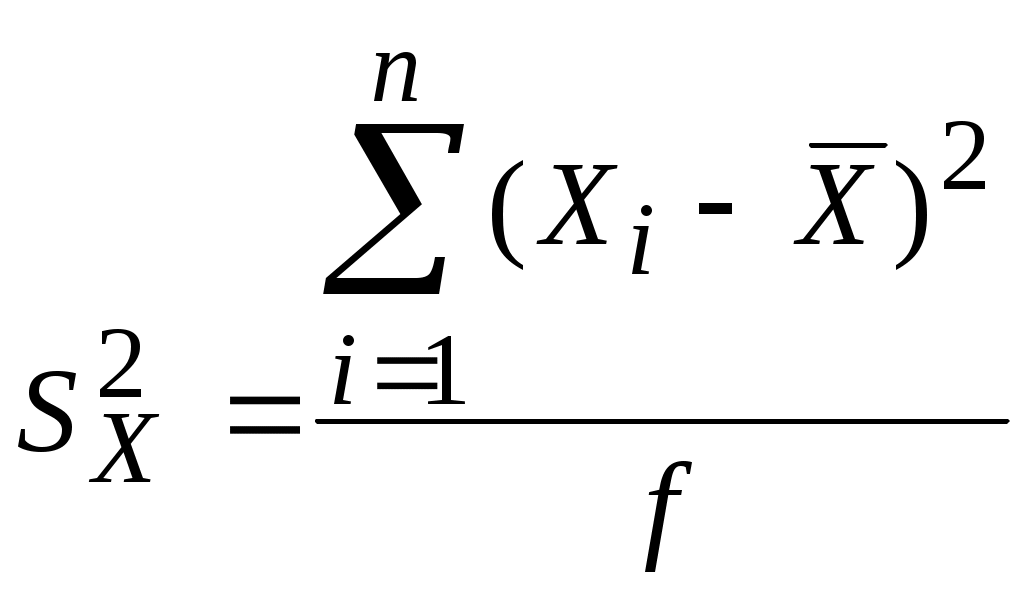или ):

(5.2)

Число степеней свободы f = [общее число измерений] – [число оценок, уже рассчитанным по этим измерениям и примененным в текущей формуле]. В данном случае уже рассчитана и используется величина , т.е. .

, среднее квадратичное отклонение (ошибка, стандарт).

Оценка дисперсии воспроизводимости Y (обозначается 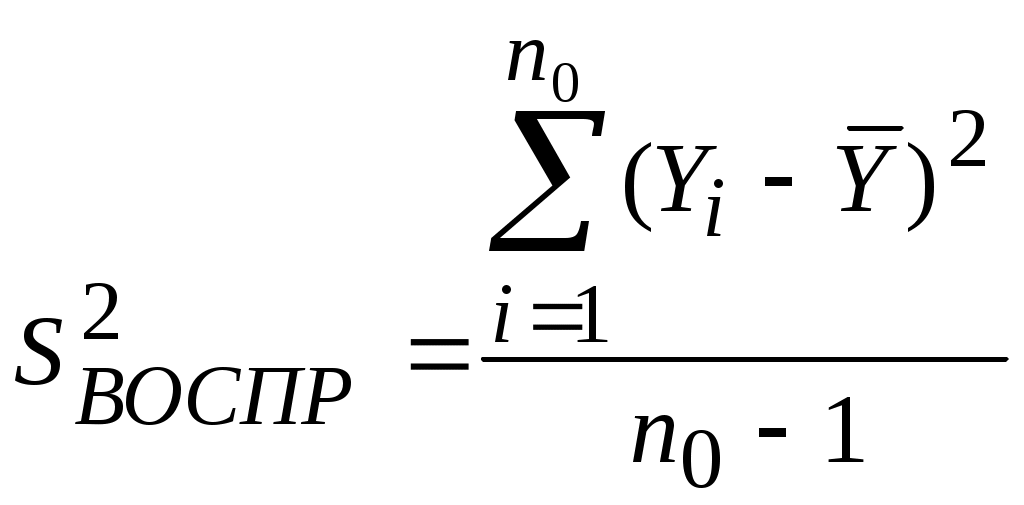или ):

(5. 3)

ил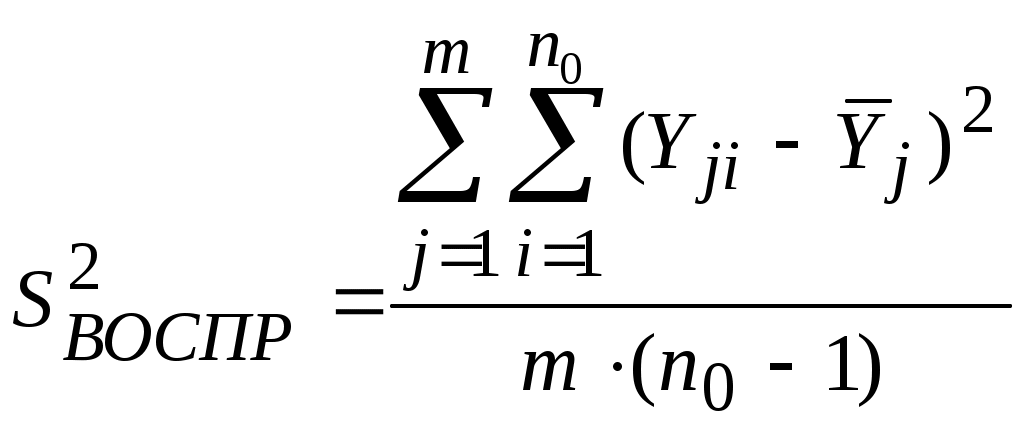и (5.3А)

- ошибка опыта (ошибка воспроизводимости, среднеквадратическая ошибка, среднеквадратическое отклонение -СКО).(См [1] стр.37)

Оценка остаточной дисперсии Y (дисперсии адекватности):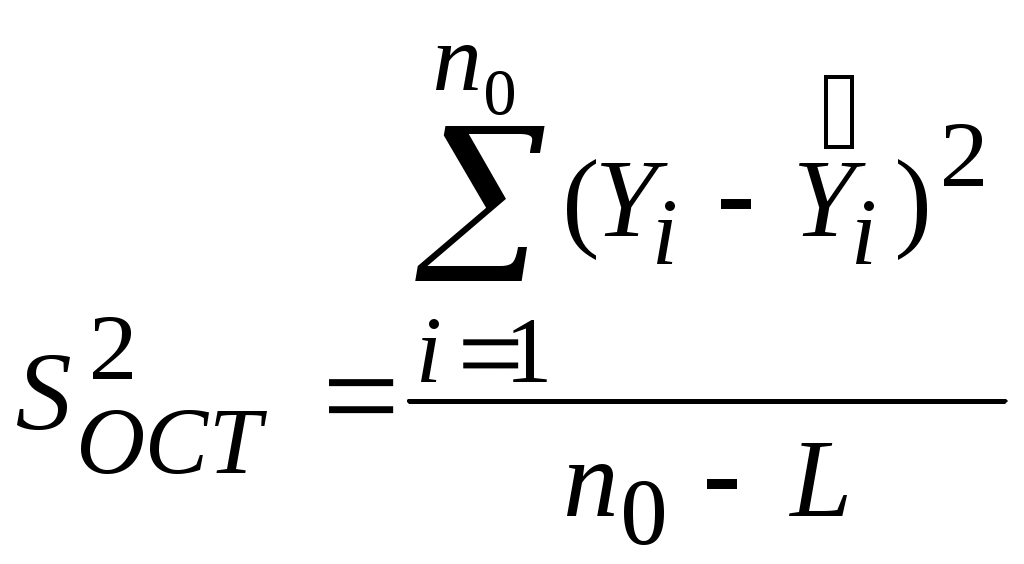

(5.4)

- расчетное значение выхода; L – количество коэффициентов в уравнении регрессии;

Нормальное распределение.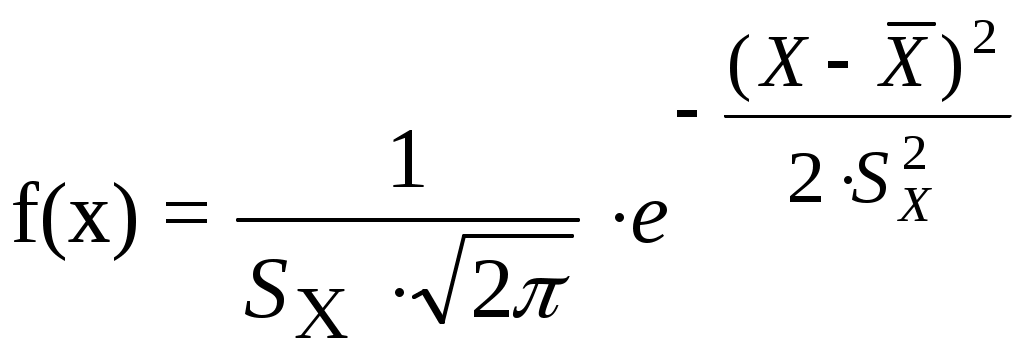

(- < x < ) (5.5)
Критерий Стьюдента. t-критерий Стьюдента - общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.

t-критерий был разработан Уильямом Госсетом (1876-1937) для оценки качества пива на пивоваренных заводах Гиннесса в Дублине (Ирландия). В связи с обязательствами перед компанией по неразглашению коммерческой тайны (руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Магистрант).

Критерий Стьюдента направлен на оценку различий величин средний значений двух выборок, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных выборок, причем выборки могут быть не равны по величине см.[4].

Условия применения t-критерия Стьюдента.Для применения t-критерия Стьюдента необходимо соблюдать следующие условия:

1. измерение может быть проведено в шкале интервалов и отношений.

2. сравниваемые выборки должны быть распределены по нормальному закону.

Критерий Стьюдента позволяет определить значимость коэффициентов уравнения регрессии. b_i. (используется для проверки гипотезы значимости коэффициентов). Для этого для каждого из L коэффициентов b_i. Рассчитывают по формуле:

, (5.6)
если > , то b_i считается значимым, в противном случае он не значимым и приравнивается к нулю.

, (5.7)
- среднеквадратическая ошибка в определении коэффициента регрессии b_i;

- табличное значение критерия Стьюдента при f = n0 – 1 или f =m (n0 – 1);

Иногда незначимость b_i может быть вызвана и другими причинами, например, неверным интервалом варьирования при подготовке к эксперименту. Ниже приведен пример на Mathcad использования критерия Стьюдента. [1, стр.164].

Сделаем замечание относительно проблемы оценки значимости коэффициентов уравнения регрессии (2.2). Если какой-либо коэффициент незначим, то он может быть принят равным нулю, т.к. его влияние на результат расчета по формуле (2.2) мало. Чтобы оценить допустимый предел требуемой точности определения расчетного значения выхода надо учесть, что в инженерной и научной практике обычно достаточно 3-5 значащих цифр при записи и использовании числовых расчетов. Для обоснованного отброса незначимых коэффициентов необходимо иметь информацию о дисперсии, присущей экспериментально найденным значениям выхода Y, а также значениям расчетным . Строго говоря, экспериментально найденные значения Y являются случайными величинами. Дисперсия случайной величины — это мера разброса данной случайной величины, то есть мера её отклонения от математического ожидания (т.е. среднеарифметического от ряда параллельных экспериментальных измерений). Если дисперсия эксперимента превышает допустимую величину, то доверять таким экспериментам нельзя, т.к. они невоспроизводимы. Это может происходить при низкой точности измерительных приборов, неправильной методики эксперимента, неучета дополнительных факторов, влияющих на результаты эксперимента, взаимного влияния входов друг на друга и т.п. Вообще говоря, отбрасывание незначимых коэффициентом актуально, когда уравнение (1) используется при ручном расчете, например, с использованием калькуляторов. При использовании же при расчете компьютерных технологий отбрасывание незначимых коэффициентов можно не проводить.



Таким образом, в этом примере Lзн = 4
Критерий Кохрена используют при сравнении трёх и более выборок одинакового объёма n. Расхождение между дисперсиями считается случайным при выбраном уровне значимости p, если:

где  — квантиль случайной величины G при числе суммируемых дисперсий m и числе степеней свободы f = n − 1.
Критерий Кохрена применяется для проверки воспроизводимости опытов (для проверки гипотезы воспроизводимости опытов):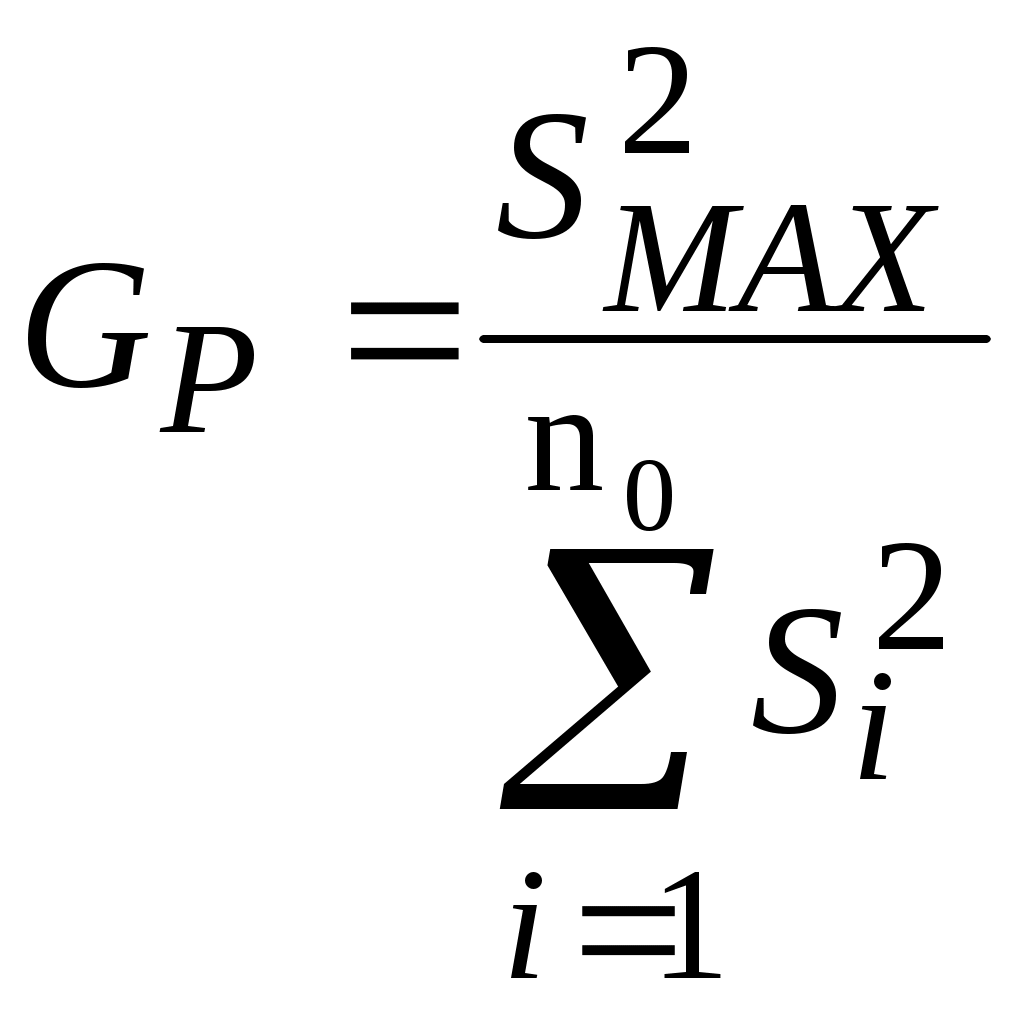

, (5.8)

т.е. расчетное значение GP определяется как отношение наибольшей из оценок дисперсий к сумме всех найденных оценок дисперсий.

Если расчетное GР > GТАБ, то дисперсии неоднородны, т.е. значения Y не подчиняются нормальному закону распределения, а опыты невоспроизводимы). - наибольшая из оценок выборочных дисперсий;

n0 – общее число сравниваемых дисперсий (количество параллельных (дублирующих) опытов);

- сумма всех оценок дисперсий. Количество опытов в серии должно быть одинаковым, в противном случае можно воспользоваться критерием Бартлетта. Необходимо знать: n0 и число степеней свободы f = n0 - 1. Если опыты невоспроизводимы, то можно попытаться выявить и устранить источники невоспроизводимости (помехи), увеличить точность измерения и т.п. Если воспроизводимость не может быть обеспечена, то и результаты эксперимента не могут быть использованы для дальнейшей математической обработки. Например, (см. таб.) рассмотрим эксперимент, состоящий из трех серий (m = 3) по два параллельных опыта (n0 = 2). В них выход Y зависит от двух факторов X1 и X2.



Расчетное значение критерия Кохрена GР = 1.28/2.5 = 0.51, в таб. (при m = 3 и f = n0 – 1 = 1) находим GТАБ = 0.967, т.к. GР < GТАБ, то опыты воспроизводимы, а оценки дисперсий можно считать однородными.

Вычислим также оценку дисперсии воспроизводимости: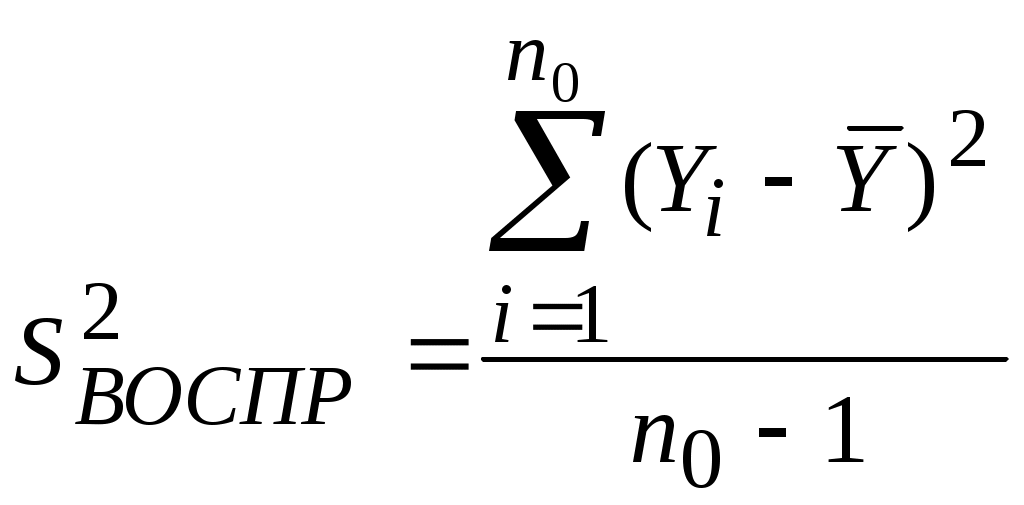

=(0.50 + 0.72 + 1.28)/3 = 0.83, с ней связано число степеней свободы f = m(n0 - 1) = 3(2-1) = 3.

Основная литература

1. 
   Советов Б.Я., Яковлев С.А. Моделирование систем. – М.: Высшая школа. 2001
   
2. 
   Авдеев П. Ф. Философия информационной цивилизации. — M.: ВЛАДОС, 1994
   

Дополнительная литература

3. 
   Гроп Д. Методы идентификации систем. - М.: Мир, 1979.
   
4. 
   Эйкхофф П. Основа идентификации систем управления. - М.: Мир, 1975.
   
5. 
   Автоматический расчет t-критерия Стьюдента, сайт http://www.psychol-ok.ru/statistics/student/