Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
 Скачать 4.07 Mb. Скачать 4.07 Mb.
|
Лекция 3 Постановка задачи моделирования и идентификации статических характеристик объектовМатематические модели статических (ММС) объектов Постановка задачи моделирования и идентификации статических характеристик объектов (см рисунок 3.1). 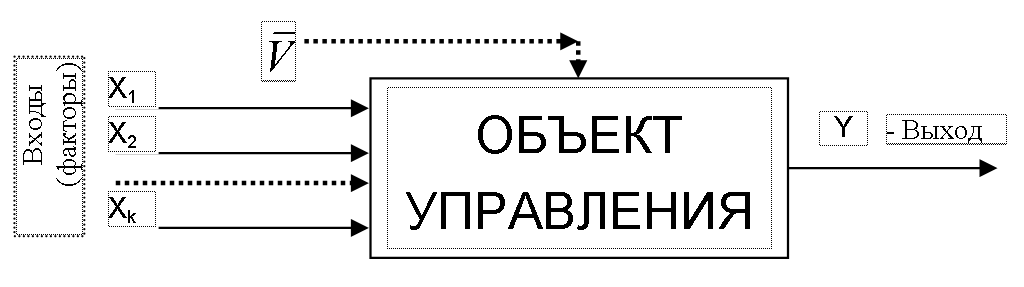 Рисунок 3.1 - Структура объекта статики Статические характеристики широко применяются при расчете и исследовании систем в условиях установившихся состояний, когда все переходные процессы или завершились, или ими можно пренебречь. Характерной особенностью ММС является то, что в них отсутствуют производные по времени. В общем виде ММС объекта – функция отклика, связывающая входные параметры Х с входными где N0, n0, – количество параллельных (дублирующих) опытов или опытов в центре плана; m – количество серий параллельных опытов; k - количество входов (факторов, степень полинома); NEX – число экспериментальных точек плана; L; LЗН – соответственно количество всех и значимых коэффициентов в уравнении регрессии; Например, чисто применяют вид уравнения для k=3 (L =10): Могут применяться и другие виды ММС, в том числе и отражающие физическую природу изучаемого явления или объекта. Выбор модели вида (**) обусловлен его простотой, и , достаточно большой точностью описания исследуемых зависимостей. Дополнительные замечания по поводу выбора вида математической модели (уравнения регрессии). Традиционно используется вид (**), при необходимости (если уравнение не адекватно описывает эксперимент) могут быть добавлены члены вида В этой лекции нами будут рассмотрены элементы теории дисперсионного анализа, статистической оценки параметров распределения случайных величин и проверки статистических гипотез, используемых при практическом решении задач идентификации и в лабораторном практикуме по дисциплине. Перечислим кратко назначение методов анализа, применяемых при идентификации. Дисперсионный анализ применяется для исследования влияния одной или нескольких качественных переменных (факторов) на одну зависимую количественную переменную (отклик). Анализ временных рядов применим к одиночным или связанным временным рядам и позволяет выделять различные формы периодичности и взаимовлияния временных процессов, а также осуществлять прогнозирование будущего поведения временного ряда. Регрессионные процедуры позволяют рассчитать модель, описываемую некоторым уравнением и отражающую функциональную зависимость между экспериментальными количественными переменными, а также проверяют гипотезу об адекватности модели экспериментальным данным. По полученным результатам можно оценить природу и степень зависимости переменных и предсказать новые значения зависимой переменной. Корреляционный анализ – это группа статистических методов, направленная на выявление и математическое представление структурных зависимостей между выборками. Кластерный анализ осуществляет разбиение объектов на заданное число удаленных друг от друга классов, а также строит дерево классификаций объектов посредством иерархического объединения их в группы (кластеры). Основной задачей факторного анализа является нахождение в многомерном пространстве первичных переменных (значения которых регистрируются в эксперименте), сокращенной системы вторичных переменных (факторов). Метод факторного анализа первоначально был разработан в психологии с целью выделения отдельных компонентов человеческого интеллекта из многомерных данных по измерению различных проявлений умственных способностей. Методы контроля качества предназначены для контроля выпускаемой продукции с целью выявления нарушений и узких мест в организации производства и в технологических процессах, ведущих к снижению качества продукции. Дисперсионный анализ (от латинского Dispersio – рассеивание / на английском Analysis Of Variance - ANOVA) применяется для исследования влияния одной или нескольких качественных переменных (факторов) на одну зависимую количественную переменную (отклик). В основе дисперсионного анализа лежит предположение о том, что одни переменные могут рассматриваться как причины (факторы, независимые переменные), а другие как следствия (зависимые переменные). Независимые переменные называют иногда регулируемыми факторами именно потому, что в эксперименте исследователь имеет возможность варьировать ими и анализировать получающийся результат. Основной целью дисперсионного анализа (ANOVA) является исследование значимости различия между средними с помощью сравнения (анализа) дисперсий. Разделение общей дисперсии на несколько источников, позволяет сравнить дисперсию, вызванную различием между группами, с дисперсией, вызванной внутригрупповой изменчивостью. При истинности нулевой гипотезы (о равенстве средних в нескольких группах наблюдений, выбранных из генеральной совокупности), оценка дисперсии, связанной с внутригрупповой изменчивостью, должна быть близкой к оценке межгрупповой дисперсии. Если вы просто сравниваете средние в двух выборках, дисперсионный анализ даст тот же результат, что и обычный t-критерий для независимых выборок (если сравниваются две независимые группы объектов или наблюдений) или t-критерий для зависимых выборок (если сравниваются две переменные на одном и том же множестве объектов или наблюдений). Сущность дисперсионного анализа заключается в расчленении общей дисперсии изучаемого признака на отдельные компоненты, обусловленные влиянием конкретных факторов, и проверке гипотез о значимости влияния этих факторов на исследуемый признак. Сравнивая компоненты дисперсии друг с другом посредством F—критерия Фишера, можно определить, какая доля общей вариативности результативного признака обусловлена действием регулируемых факторов. Исходным материалом для дисперсионного анализа служат данные исследования трех и более выборок: которые могут быть как равными, так и неравными по численности, как связными, так и несвязными. По количеству выявляемых регулируемых факторов дисперсионный анализ может быть однофакторным (при этом изучается влияние одного фактора на результаты эксперимента), двухфакторным (при изучении влияния двух факторов) и многофакторным (позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие). Дисперсионный анализ относится к группе параметрических методов и поэтому его следует применять только тогда, когда доказано, что распределение является нормальным. Дисперсионный анализ используют, если зависимая переменная измеряется в шкале отношений, интервалов или порядка, а влияющие переменные имеют нечисловую природу (шкала наименований). Однофакторный дисперсионный анализ используется для проверки гипотезы о сходстве средних значений двух или более выборок, принадлежащих одной и той же генеральной совокупности. Этот метод распространяется также на тесты для двух средних (к которым относится, например, t-критерий). Двухфакторный дисперсионный анализ с повторениями - Представляет собой более сложный вариант однофакторного анализа, включающее более чем одну выборку для каждой группы данных. Двухфакторный дисперсионный анализ без повторения - Представляет собой двухфакторный анализ дисперсии, не включающий более одной выборки на группу. Используется для проверки гипотезы о том, что средние значения двух или нескольких выборок одинаковы (выборки принадлежат одной и той же генеральной совокупности). Этот метод распространяется также на тесты для двух средних, такие как t-критерий. Теоретические основы. В любом эксперименте среднее значение наблюдаемых величин меняется в связи с изменением входных факторов, определяющих условия эксперимента, а также и случайных факторов (помех). Исследование влияния тех или иных факторов на изменчивость средних значений и является задачей дисперсионного анализа. Дисперсионный анализ состоит в выделении и оценке отдельных факторов, вызывающих изменчивость изучаемой случайной величины. Для этого производится разложение суммарной выборочной дисперсии на составляющие, обусловленные независимыми факторами. Для того чтобы определить значимо ли влияние данного фактора необходимо оценить значимость соответствующей выборочной дисперсии в соответствии с дисперсией воспроизводимости, обусловленной случайными факторами. Предположим, что результат эксперимента зависит от некоторого одиночного фактора А, который принимает n различных значений (n-количество серий опытов). Для каждой серии опытов проводится m повторных наблюдений, результаты которых можно записать в следующем виде: Y11 Y12 Y13 ... Y1m Y21 Y22 Y23 ... Y2m Y31 Y32 Y33 ... Y3m ... ... ... ... ... Yn1 Yn2 Yn3 ... Ynm На основе полученных статистических данных требуется проверить гипотезу о равенстве математических ожиданий для каждой конкретной серии. Если проверяемая гипотеза верна, то средние арифметические значения для всех серий практически не отличаются друг от друга, в противном случае предполагаемая гипотеза должна быть отвергнута. Обозначим через 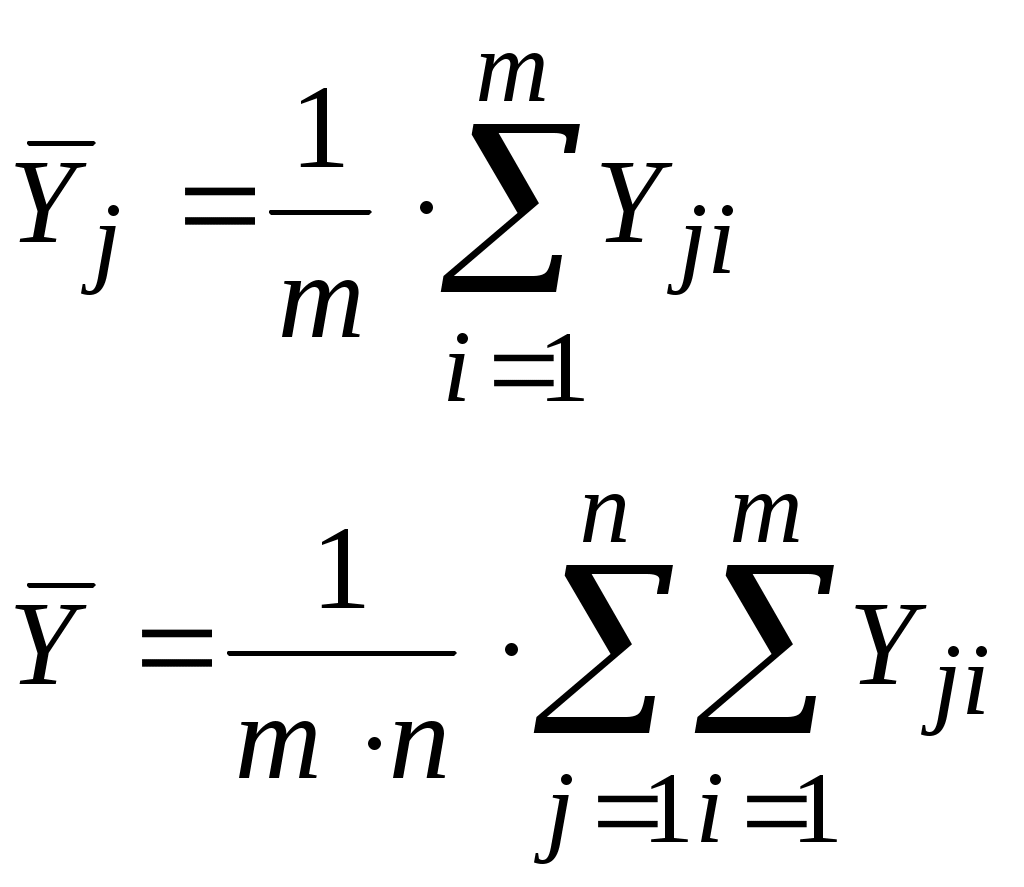 (3.1) (3.1)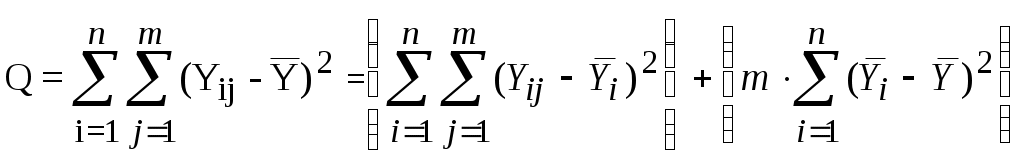 (3.2) (3.2)Сущность дисперсионного анализа состоит в разложении суммы квадратов отклонений отдельных Yij от общего среднего на две суммы: Q - определяет общее отклонение значения каждого опыта (Yij) от среднего; QА - характеризует рассеяние, вызванное фактором А (выражение во-вторых фигурных скобках); Qост - характеризует рассеяние, вызванное случайными помехами (выражение в первых фигурных скобках). Разделив суммы квадратов отклонений на соответствующие степени свободы получим следующие дисперсии: σ2 = Q/f σА2= QA/f1 (3.3) σОСТ2 = Qост/f2 Число степеней свободы f = m·n -1 f1 = n - 1 f2 = n·(m-1) Проведение дисперсионного анализа состоит в сравнении оценок σА2и σОСТ2. Если гипотеза о том, что математические ожидания для каждой серии равны, верна, то σА2 не должна существенно превышатьσОСТ2, что проверяется по критерию Фишера: F = σА2/σОСТ2 (3.4) Если F < Fкр, то различие между σА2 и σОСТ2 можно считать несущественным, т.е. влияние фактора А сравнимо с влиянием случайных помех. Если F > Fкр, то различие между σА2 и σОСТ2 существенно, т.е. фактор А оказывает влияние на выходную величину. Значение Fкр определяют по квантилям распределения Фишера, при уровне значимости α ("альфа") и степеням свободы f1 и f2: Fкр = f( α , f1, f2) Статистическая оценка параметров распределения случайных величин Проверка гипотез Статистическая гипотеза (statistical hypothesys) — это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных. Проверка статистической гипотезы (testing statistical hypotheses) — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных. Статистический тест или статистический критерий — строгое математическое правило, по которому принимается или отвергается статистическая гипотеза. Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое на основе выборки. Примерами статистических гипотез являются предположения: генеральная совокупность распределена по экспоненциальному закону; математические ожидания двух экспоненциально распределенных выборок равны друг другу. В первой из них высказано предположение о виде закона распределения, а во второй – о параметрах двух распределений. Гипотезы, в основе которых нет никаких допущений о конкретном виде закона распределения, называют непараметрическими, в противном случае – параметрическими. Гипотезу, утверждающую, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, на основании которых производится сравнение, называют нулевой (основной) гипотезой и обозначают Н0. Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н1. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза. Различают простые и сложные гипотезы. Гипотезуназывают простой, если она однозначно характеризует параметр распределения случайной величины. Например, если θ является параметром экспоненциального распределения, то гипотеза Н0 о равенстве θ =10 – простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н0 о неравенстве θ >10 состоит из бесконечного множества простых гипотез Н0 о равенстве θ =bi , где bi – любое число, большее 10. Гипотеза Н0 о том, что математическое ожидание нормального распределения равно двум при неизвестной дисперсии, тоже является сложной. Сложной гипотезой будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии. Проверка гипотезы основывается на вычислении некоторой случайной величины – критерия, точное или приближенное распределение, которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки z=z(x1, x2, …, xn). Процедура проверки гипотезы предписывает каждому значению критерия одно из двух решений – принять или отвергнуть гипотезу. Тем самым все выборочное пространство и соответственно множество значений критерия делятся на два непересекающихся подмножества S0 и S1. Если значение критерия z попадает в область S0, то гипотеза принимается, а если в область S1, – гипотеза отклоняется. Множество S0 называется областью принятия гипотезы или областью допустимых значений, а множество S1 – областью отклонения гипотезы или критической областью. Выбор одной области однозначно определяет и другую область. При заданном объеме выборки вероятность совершения ошибки первого рода можно уменьшить, снижая уровень значимости α. Однако при этом увеличивается вероятность ошибки второго рода (снижается мощность критерия). Аналогичные рассуждения можно провести для случая, когда истинное значение параметра равно Т – d. Единственный способ уменьшить обе вероятности состоит в увеличении объема выборки (плотность распределения оценки параметра при этом становится более "узкой"). При выборе критической области руководствуются правилом Неймана – Пирсона: следует так выбирать критическую область, чтобы вероятность α была мала, если гипотеза верна, и велика в противном случае. Однако выбор конкретного значения α относительно произволен. Употребительные значения лежат в пределах от 0,001 до 0,2. В целях упрощения ручных расчетов составлены таблицы интервалов с границами θ 1– α /2 и θ α /2 для типовых значений α и различных способов построения критерия. При выборе уровня значимости необходимо учитывать мощность критерия при альтернативной гипотезе. Иногда большая мощность критерия оказывается существеннее малого уровня значимости, и его значение выбирают относительно большим, например, 0,2. Такой выбор оправдан, если последствия ошибок второго рода более существенны, чем ошибок первого рода. Например, если отвергнуто правильное решение "продолжить работу пользователей с текущими паролями", то ошибка первого рода приведет к некоторой задержке в нормальном функционировании системы, связанной со сменой паролей. Если же принято решения не менять пароли, несмотря на опасность несанкционированного доступа посторонних лиц к информации, то эта ошибка повлечет более серьезные последствия. В зависимости от сущности проверяемой гипотезы и используемых мер расхождения оценки характеристики от ее теоретического значения применяют различные критерии. К числу наиболее часто применяемых критериев для проверки гипотез о законах распределения относят критерии хи-квадрат Пирсона, Колмогорова, Мизеса, Вилкоксона, о значениях параметров – критерии Фишера, Стьюдента. Рассмотрим практическую методику использования метода статистической оценка параметров распределения. Состоятельные и несмещенные оценки основных параметров распределения случайной величины (СВ) (математического ожидания MX и дисперсии σХ2) могут быть получены по формулам:  где n - объем выборки. Оценку коэффициента корреляции между случайными величины X и Y определяют по формуле: 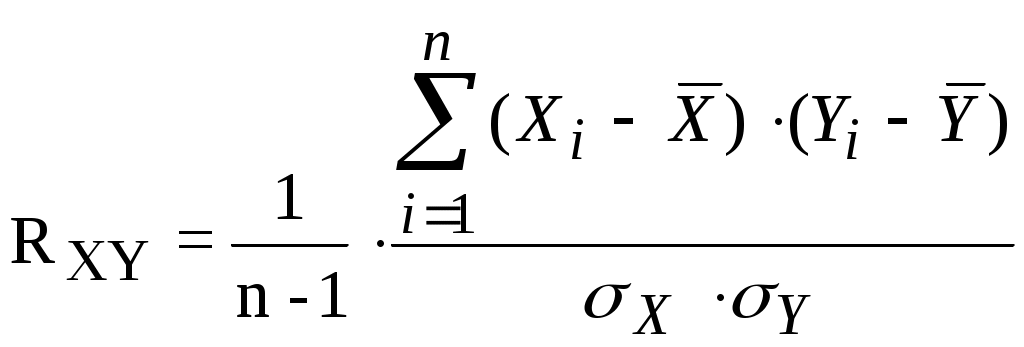 (3.7) (3.7)Так как оценки (3.5) - (3.6) определяют по выборке конечного объема, возникает вопрос об их статистической достоверности и точности. Обозначим θ как оценку интересующего нас параметра. Тогда задача определения достоверности и точности оценки сводится к определению такого интервала (θ1, θ2), включающего параметр θ, что с вероятностью 1 - α (где α - достаточно малая величина, равная 0.1, 0.05, 0.01 …) можно утверждать, что неизвестное истинное значение параметра находится в этом интервале. Интервал (θ1, θ2) называют доверительным интервалом, а вероятность 1- α доверительной вероятностью. Рассмотрим случай, когда величина X имеет нормальный закон распределения с плотностью вероятности: 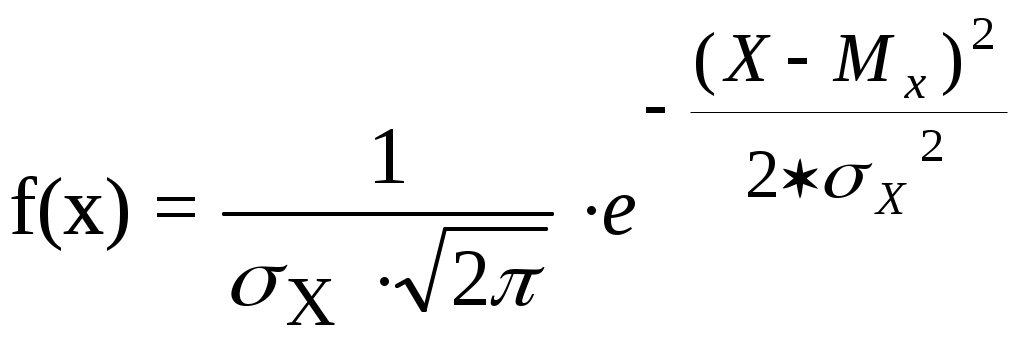 (3.8) (3.8)Доверительный интервал для математического ожидания: которое можно представить в виде: Введем параметр: имеющий t-распределение Стьюдента с v = n - 1 степенями свободы. Тогда равенство (3.4) перепишется в виде: где t(a, v) определяют по таблице распределения Стьюдента при вероятности α и степени свободы v = n - 1. Доверительный интервал для Mx, соответствующий доверительной вероятности 1 - α, есть: Чтобы определить доверительный интервал для дисперсии, необходимо найти границы интервала σ12и σ22, удовлетворяющие равенству: P[σ12 < σX2 < σ22] = 1 - α (3.13) Для нормально распределенного X известен закон распределения величины со степенями свободы v = n - 1: χ2 = (n-1)·σX2/ σ 2, (3.14) где σX2-выборочная дисперсия, σ2-истинное значение σX2 После подстановки (3.14) в (3.13), при условии, что: P[σX2<σ12]=P[σX2>σ22] = α/2, получим: P[χ2(1-α/2, v) < (n-1)·σX2/σ2 < χ2(α/2, v)] = 1 - α. Величину χ2(1-α/2,v)=(n-1)·σX2/σ22находят по таблице распределения Пирсона при вероятности 1-α/2 и числе степеней свободы v=n-1, а χ2(α/2, v)=(n-1)·σX2/σ2определяют при вероятности α/2 и числе степеней свободы v = n - 1. Следовательно, доверительный интервал для дисперсии σX2, соответствующий доверительной вероятности 1 - α, есть: 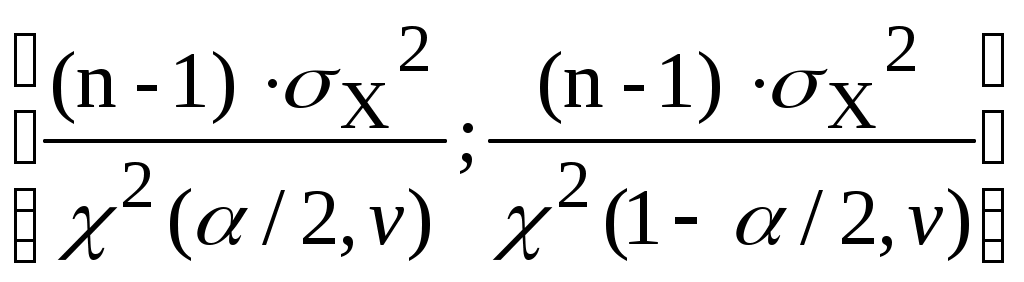 (3.14) (3.14)Алгоритм проверки статистических гипотез. Понятие статистической гипотезы означает предположение о виде распределения СВ или о некотором параметре ее распределения. Проверка гипотезы заключается в сопоставлении определенного статистического показателя (критерия значимости), вычисленного по данной выборке, с критерием значимости, найденным теоретически при условии, что проверяемая гипотеза верна. 1)При проверке гипотезы о том, что Mx = C, в качестве критерия используют величину: Эта величина при условии, что гипотеза верна, имеет t-распределение Стьюдента с v = n - 1 степенями свободы. Если вычисленное по соотношению (3.15) значение t по абсолютной величине не превышает критического значения tкр=t(α, v), найденного по таблице t-распределения при уровне значимости α и числе степеней свободы v, то гипотеза о том, что Mx=C принимается, в противном случае она отвергается. 2)Проверку гипотезы о равенстве двух математических ожиданий Mx = My, вычисленных по двум выборкам случайных величин X и Y объемами n1 и n2 проводят по критерию: t = (X-Y)/σX-Y (3.16) 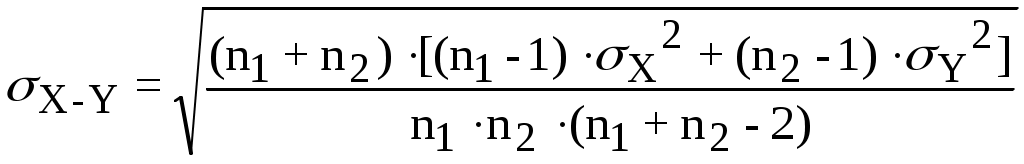 (3.17) (3.17)Критерий t имеет t-распределение Стьюдента с числом степеней свободы v = n1 + n2 - 2. Проверку гипотезы проверяют также, как и в предыдущем случае, т.е. при |t|<=tкр гипотеза принимается, а при |t|>tкр отвергается. 3)Проверку гипотезы о равенстве дисперсий двух СВ X и Y, оценки которых σX2 и σY2 определены по двум выборкам объемом n1 и n2, проводят с использованием критерия: F = σX2/σY2, (3.18) который имеет распределение Фишера со степенями свободы v1 = n1 - 1 для числителя и v2 = n2 - 1 для знаменателя. Полученное по критерию (3.18) значение сравнивают с критическим Fкр=F(α, v1, v2). Если F 4)При проверке гипотезы об отсутствии корреляции между двумя СВ используют соотношение: t = Rxy/σR, (3.19) где: Rxy-оценка коэффициента корреляции, найденная по (3.7), σR2= [(1-Rxy2)/(n-2)] Величина t имеет t-распределение Стьюдента с v = n - 2 степенями свободы. Если вычисленное по соотношению (3.19) значение t по абсолютной величине не превышает критического значения tкр=t(α, v), найденного по таблице t-распределения при уровне значимости α и числе степеней свободы v, нет оснований для того, чтобы гипотеза об отсутствии корреляции на генеральной совокупности была отвергнута, в противном случае принимаем, что между величинами X и Y существует корреляция. Основная литература Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с. Рузинов Л.П. Статистические методы оптимизации химических процессов. -М.: Химия, 1972 Дополнительная литература Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с. |
