Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление

• Название: Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
• Дата: 24.01.2023
• Размер: 4.07 Mb.
• Имя файла: Лекц комплекс СМИОСУ 2017.doc
• Тип: Конспект лекций; #902228
• страница: 3 из 29

Тема 2 Математические модели объектов идентификации

Лекция 2 Основнные понятия и терминология дисциплины

Классификация математических моделей

Могут быть предложены различные методы классификации моделей объектов и систем, рассмотрим основные из них.

Физические модели. В основу классификации положена степень абстрагирования модели от оригинала. Предварительно все модели можно подразделить на две группы: материальные (физические) и абстрактные (математические). Физической моделью обычно называют систему, которая эквивалентна или подобна оригиналу, либо у которой процесс функционирования такой же, как у оригинала, и имеет ту же или другую физическую природу. Можно выделить следующие виды физических моделей: натурные, квазинатурные, масштабные и аналоговые.

Натурные модели — это реальные исследуемые системы. Их называют макетами и опытными образцами. Натурные модели имеют полную адекватность с системой-оригиналом, что обеспечивает высокую точность и достоверность результатов моделирования. Процесс проектирования ВС завершается зачастую испытанием опытных образцов. Квазинатурные модели представляют собой совокупность натурных и математических моделей. Этот вид моделей используется в случаях, когда математическая модель части системы не является удовлетворительной (например, модель человека-оператора) или, когда часть системы должна быть исследована во взаимодействии с остальными частями, но их еще не существует, либо их включение в модель затруднено или дорого. Примерами квазинатурных моделей могут служить вычислительные полигоны, на которых отрабатывается программное обеспечение различных систем, или реальные АСУ, исследуемые совместно с математическими моделями соответствующих производств.

Масштабная модель — это система той же физической природы, что и оригинал, но отличающаяся от него масштабами. Методологической основой масштабного моделирования является теория подобия, которая предусматривает соблюдение геометрического подобия оригинала и модели и соответствующих масштабов для их параметров. При проектировании ВС масштабные модели могут использоваться для анализа вариантов компоновочных решений по конструкции системы и ее элементов.

Аналоговыми моделями называются системы, имеющие физическую природу, отличающуюся от оригинала, но сходные с оригиналом процессы функционирования. Обязательным условием при этом является однозначное соответствие между параметрами изучаемого объекта и его модели, а также тождественность безразмерных математических описаний процессов, протекающих в них. Для создания аналоговой модели требуется наличие математического описания изучаемой системы. В качестве аналоговых моделей' используются механические, гидравлические, пневматические системы, но наиболее широкое применение получили электрические и электронные аналоговые модели, в которых сила тока или напряжение являются аналогами физических величин другой природы. Особенностью аналоговых моделей является их гибкость и простота адаптации к изменению и измерению количественных значений параметров и характеристик моделируемой системы. Аналоговые модели используют при исследовании средств вычислительной техники на уровне логических элементов и электрических цепей, а также на системном уровне, когда функционирование системы описывается, например, дифференциальными или алгебраическими уравнениями.

Математические модели. Математическая модель представляет собой формализованное описание системы с помощью абстрактного языка, в частности с помощью математических соотношений, отражающих процесс функционирования системы. Для составления модели можно использовать любые математические средства — алгебраическое, дифференциальное и интегральное исчисление, теорию множеств, теорию алгоритмов и т. д. По существу, вся математика создана для составления и исследования моделей объектов или процессов.

К средствам абстрактного описания систем относятся также языки химических формул, схем, чертежей, карт, диаграмм и т. п. Выбор вида модели определяется особенностями изучаемой системы и целями моделирования, так как исследование модели позволяет получить ответы на определенную группу вопросов. Для получения другой информации может потребоваться модель другого вида.

Цели моделирования и характерные черты оригинала определяют в конечном счете ряд других особенностей моделей и методы их исследования. Например, математические модели можно классифицировать на детерминированные и вероятностные (стохастические). Первые устанавливают однозначное соответствие между параметрами и характеристиками модели, а вторые — между статистическими значениями этих величин. Выбор того или иного вида модели обусловлен степенью необходимости учета случайных факторов. Среди математических моделей можно выделить по методу их исследования аналитические, численные и имитационные модели.

Аналитической моделью называется такое формализованное описание системы, которое позволяет получить решение уравнения в явном виде, используя известный математический аппарат.

Численная модель характеризуется зависимостью такого вида, который допускает только частные численные решения для конкретных начальных условий и количественных параметров модели.

Имитационная модель — это совокупность описания системы и внешних воздействий, алгоритмов функционирования системы или правил изменения состояния системы под влиянием внешних и внутренних возмущений. Эти алгоритмы и правила не дают возможности использования имеющихся математических методов аналитического и численного решения, но позволяют имитировать процесс функционирования системы и производить измерения интересующих характеристик.

Многообразие систем и объектов, проявляющееся в многообразии их структурно-функциональной организации, определяет использование множества разных моделей, которые могут быть классифицированы в зависимости от:

1) характера функционирования исследуемой системы:

• 
  детерминированные, функционирование которых описывается детерминированными величинами;
  
• 
  стохастические или вероятностные, функционирование которых описывается случайными величинами.
  

2) характера протекающих в исследуемой системе процессов:

• 
  непрерывные, в которых процессы протекают непрерывно во времени;
  
• 
  дискретные, в которых процессы меняют свое состояние в дискретные моменты времени.
  

3) степени достоверности исходных данных об исследуемой системе:

• 
  с априорно известными параметрами;
  
• 
  с неизвестными параметрами.
  

4) режима функционирования системы:

• 
  стационарные, в которых характеристики не меняются со временем;
  
• 
  нестационарные, в которых характеристики изменяются со временем.
  

5) назначения:

• 
  статические или структурные, отображающие состав и структуру системы;
  
• 
  динамические или функциональные, отображающие функционирование системы во времени;
  
• 
  структурно-функциональные, отображающие структурные и функциональные особенности организации исследуемой системы.
  

6) способа представления (описания) и реализации:

• 
  концептуальные или содержательные, представляющие собой описание (в простейшем случае словесное) наиболее существенных особенностей структурно-функциональной организации исследуемой системы;
  
• 
  физические или материальные - модели, эквивалентные или подобные оригиналу (макеты) или процесс функционирования, которых такой же как у оригинала и имеет ту же или другую физическую природу;
  
• 
  математические или абстрактные, представляющие собой формализованное описание системы с помощью абстрактного языка, в частности с помощью математических соотношений, отражающих процесс функционирования системы;
  
• 
  программные (алгоритмические, компьютерные), основанные на применении средств ВТ и представляющие собой обычно программный комплекс, и позволяющие наглядно и эффектно представить исследуемый объект посредством имитации или графического отображения математических зависимостей, описывающих искомый объект.
  

В дальнейшем нами основное внимание уделяется математическому моделированию, широко используемому при исследовании сложных технических систем.

Отметим, что одни и те же объекты могут быть описаны различными по сложности математическими моделями. Главным критерием выбора при этом является её адекватность исследуемому объекту.

Таким образом, задача идентификации формулируется следующим образом: по результатам наблюдений за входными и выходными переменными объекта построить оптимальную в некотором смысле его модель. При этом объект находится в нормальном режиме функционирования (т. е. в обстановке случайных возмущений и помех). Иными словами, если объект описывается некоторым неизвестным оператором F₀, то имея измеренные значения входа и выхода необходимо построить оценку , оператора объекта, оптимальную в смысле некоторого критерия.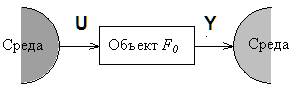



Рисунок 2.1 - Взаимодействие идентифицируемого объекта со средой
Рисунок 2.1 иллюстрирует взаимодействие идентифицируемого объекта со средой. Это взаимодействие происходит по каналам U и Y. По каналу U – вход среда воздействует на объект, а по каналу Y (выход) объект воздействует на среду. Задача идентификации сводится к определению оператора модели , связывающего вход и выход объекта Y = F(U).

Так как часто отсутствует модель среды, воздействующей на объект, то его вход естественно рассматривать как случайную функцию времени, статистические свойства которой в общем случае неизвестны. Однако известны наблюдения входа и выхода объекта, т.е. реализации функций U и Y. На объект может воздействовать ненаблюдаемые факторы V(t), которые рассматриваются как случайные помехи.

Таким образом, идентификация — это синтез оптимального в смысле некоторого критерия согласия (точности) модельного оператора исследуемого объекта с использованием результатов наблюдений за его входными и выходными переменными.

Классификация методов идентификации. В соответствии с современной теорией можно предложить следующую классификацию идентификации:

1) по конечному результату идентификации (структурная и параметрическая);

2) по способу изучения объекта идентификации (активная и пассивная)

3)по типу идентифицируемой модели (линейная и нелинейная; детерминированная и стохастическая; с непрерывным и дискретным временем; стационарная и нестационарная; одномерная и многомерная; статическая и динамическая; с сосредоточенными и распределёнными параметрами).

Активная и пассивная идентификация. Успех идентификации объекта существенно зависит от соотношения двух факторов: объема априорной информации о структуре объекта и объема измерительной информации. Априорные сведения помогают определить структуру модели, т.е. ее вид (число входов и выходов, характер связи между ними). При активном способе идентификации реализация входа формируется самим исследователем путем подачи на вход объекта испытательного сигнала желаемой формы (скачкообразного сигнала, импульсного сигнала, сигнала в виде гармонических, прямоугольных, трапецеидальных, треугольных колебаний и др.). Реализацией выхода объекта является его реакция на испытательный сигнал. При этом в современной теории идентификации широко применяются методы оптимального планирования эксперимента. При пассивном способе идентификации в качестве реализаций входа и выхода объекта принимают естественные их изменения в процессе нормального функционирования объекта.

Ha рисунке 2.2 показана связь между априорной информацией (о структуре) и апостериорной информацией об измерениях) при построении модели. Верхняя часть рисунка иллюстрирует процесс построения модели как конкретный пример использования физических законов с последующей линеаризацией и преобразованием к системе обыкновенных дифференциальных уравнений. Получающиеся уравнения определяют структуру модели. Ha каждом шаге возникают ошибки. B нижней части рисунка иллюстрируется процедура оценивания, основанная на измерениях и включающая обработку данных и алго­ритмы оценивания. Здесь также следует учесть различные виды ошибок.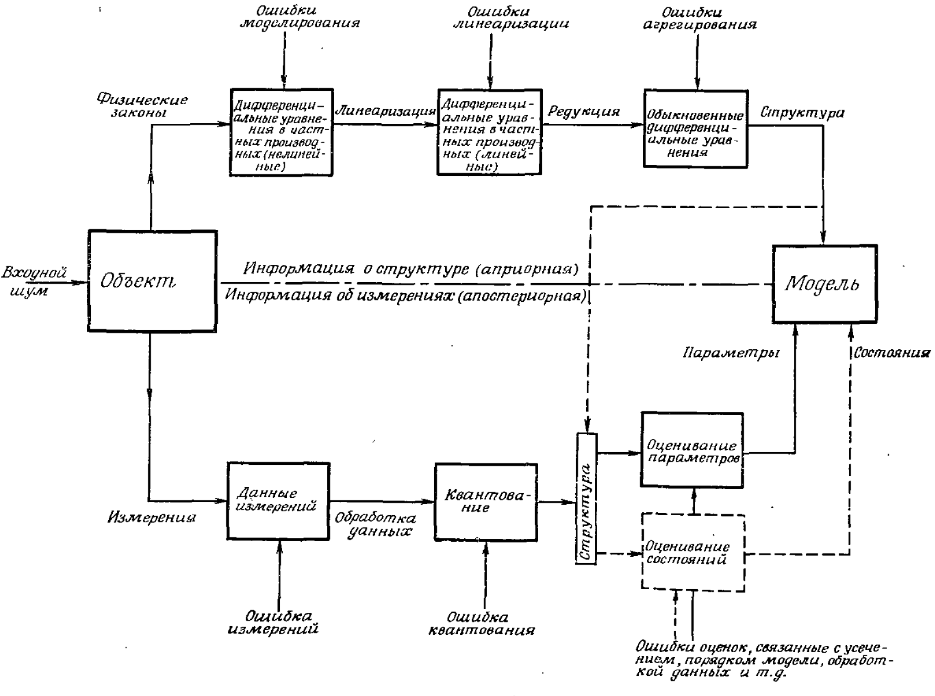



Рисунок 2.2 - Связь между априорной информацией (о структуре) и апостериорной информацией об измерениях)
Основная литература

1. 
   Советов Б.Я., Яковлев С.А. Моделирование систем. – М.: Высшая школа. 2001
   
2. 
   Авдеев П. Ф. Философия информационной цивилизации. — M.: ВЛАДОС, 1994
   

Дополнительная литература

3. 
   Исмаилов С.У. Компьютерные технологии решения задач автоматизации. Часть 1. Автоматизация схемотехнического моделирования и проектирования изделий электронной техники. Южно-Казахстанский Государственный Университет (ЮКГУ). 2002г. – 160 с., таб., ил.
   
4. 
   Гроп Д. Методы идентификации систем. - М.: Мир, 1979.
   
5. 
   Эйкхофф П. Основа идентификации систем управления. - М.: Мир, 1975.