Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
 Скачать 4.07 Mb. Скачать 4.07 Mb.
|
Лекция 7 Статические модели в форме управления регрессии и методы их определения (часть 1)Регрессионный и корреляционный анализ. В этой лекции мы рассмотрим методы регрессионного анализа, применяемые при получении статических и динамические модели в форме управления регрессии. Корреляционный анализ результатов моделирования. С помощью корреляционного анализа исследователь может установить, насколько тесна связь между двумя (или более) случайными величинами, наблюдаемыми и фиксируемыми при моделировании конкретной системы S. Корреляционный анализ результатов моделирования сводится к оценке разброса значений относительно среднего значения 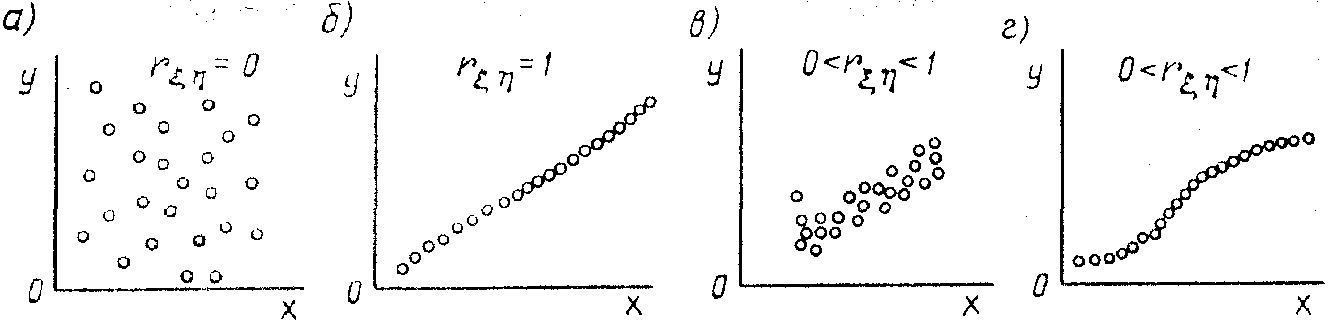 Рисунок 7.1 - Различные случаи корреляции переменных Для того чтобы оценить точность полученной при обработке результатов моделирования системы S оценки r, целесообразно ввести в рассмотрение коэффициент w = ln [(1+ r)/(1-r)]/2, причем w приближенно подчиняется гауссовскому распределению со средним значением и дисперсией: Из-за влияния числа реализаций при моделировании N на оценку коэффициента корреляции необходимо убедиться в том, что При анализе результатов моделирования системы S важно отметить то обстоятельство, что даже если удалось установить тесную зависимость между двумя переменными, то отсюда еще непосредственно не следует их причинно-следственная взаимообусловленность. Возможна ситуация, когда случайные и стохастически зависимы, хотя причинно они являются для системы S независимыми. При статистическом моделировании наличие такой зависимости может иметь место, например, из-за коррелированности последовательностей псевдослучайных чисел, используемых для имитации событий, положенных в основу вычисления значений х и у. Таким образом, корреляционный анализ устанавливает связь между исследуемыми случайными переменными машинной модели и оценивает тесноту этой связи. Однако в дополнение к этому желательно располагать моделью зависимости, полученной после обработки результатов моделирования. Регрессионный анализ результатов моделирования. Регрессионный анализ дает возможность построить модель, наилучшим образом соответствующую набору данных, полученных в ходе машинного эксперимента с системой S. Под наилучшим соответствием понимается минимизированная функция ошибки, являющаяся разностью между прогнозируемой моделью и данными эксперимента. Такой функцией ошибки при регрессионном анализе служит сумма квадратов ошибок. Дисперсионный анализ результатов моделирования. При обработке и анализе результатов моделирования часто возникает задача сравнения средних выборок. Если в результате такой проверки окажется, что математическое ожидание совокупностей случайных переменных {у{1)}, {у{2)}, …, {у{n)} отличается незначительно, то статистический материал, полученный в результате моделирования, можно считать однородным (в случае равенства двух первых моментов). Это дает возможность объединить все совокупности в одну и позволяет существенно увеличить информацию о свойствах исследуемой модели Мм, а, следовательно, и системы S. Попарное использование для этих целей критериев Смирнова и Стьюдента для проверки нулевой гипотезы затруднено в связи с наличием большого числа выборок при моделировании системы. Поэтому для этой цели используется дисперсионный анализ. Дисперсионный анализ позволяет вместо проверки нулевой гипотезы о равенстве средних значений выборок проводить при обработке результатов моделирования проверку нулевой гипотезы о тождественности выборочной и генеральной дисперсий. Возможны и другие подходы к анализу и интерпретации результатов моделирования, но при этом необходимо помнить, что их эффективность существенно зависит от вида и свойств конкретной моделируемой системы Регрессионный и корреляционный анализ широко используется при идентификация статических и динамических характеристик объектов. Задача идентификации: задавшись видом уравнения регрессии (например, вида (2.2)), определить его неизвестные коэффициенты из условия, что заданная уравнением кривая будет с достаточной точностью описывать экспериментальную характеристику. В качестве критерия соответствия при решении данной задачи берут критерий вида: min(Fbi), где Для нахождения коэффициентов bi составляют уравнения: Таким образом, получается система уравнений, решая которую можно определить bi. В конкретном случае, для выбора вида полинома используют графическое представление экспериментальной выборки, а также – априорные косвенные данные. Однако универсальных методик здесь нет. Проиллюстрируем применение метода на примере для случая, когда уравнение регрессии выбрано в виде квадратного полинома: Линейная регрессия от одного параметра. С помощью этого метода ищется минимум функции (7.1), имеющей вид суммы квадратов разностей между экспериментальными yi и расчетными: Минимизация осуществляется варьированием коэффициентов b , т.е. ищем такие b0 и b1, при которых I(b) будет минимальной. Необходимым условием минимума функции Решение этой система из двух уравнений с двумя неизвестными позволяет найти выражения для b0 и b1, при которых I(b) будет минимальной. C учетом того, что или (система нормальных уравнений, решая которую находим b0 и b1): откуда 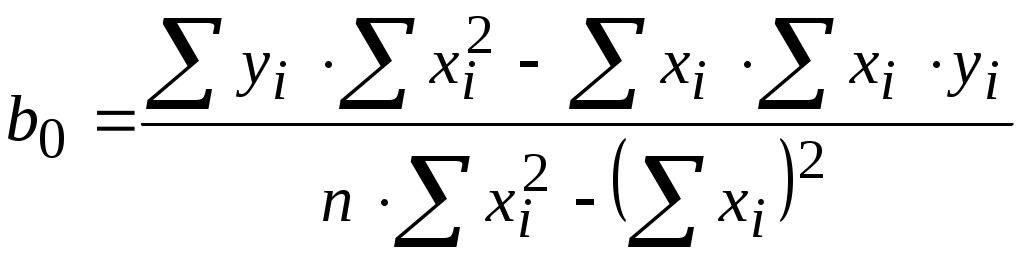 (7. 7) и (7. 7) и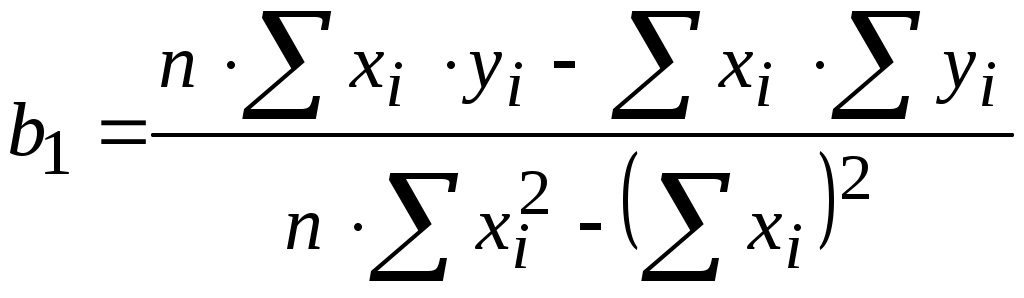 (7.8) (7.8)или проще сначала найти b1 , а затем 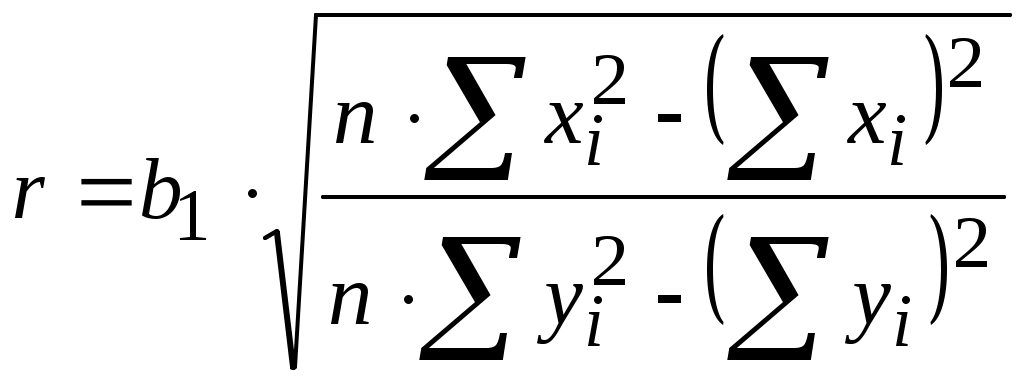 (7.9) (7.9) Пример использования см. [1, стр. 130] Основная литература Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с. Исмаилов С.У. Современные методы идентификации объектов и систем управления. Методические указания к выполнению лабораторных работ для магистрантов спец. 6М0702. Шымкент, ЮКГУ, 2010 г., -78 с. Дополнительная литература Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с. |
