Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
 Скачать 4.07 Mb.
|
Лекция 8 Статические модели в форме управления регрессии и методы их определения (часть 2)Метод множественной корреляции. Метод множественной корреляции используется при идентификации объектом с несколькими входами (k - количество входов (факторов).. При k=1 – уравнение (*) график линии, k=2 – график плоскости, k=3 – график гиперповерхности. Исходный статистический материал представлен в следующей таблице. В ней N строчек и k+2 столбцев. Таблица 8.1 Исходные данные для получения математической модели с к - входами  X0 – фиктивная переменная, равная 1, она вводится для удобства записи. Столбик X1 - значения входа номер 1, столбик X2 - значения входа номер 2 и т.д. столбик Y - значения выходов в каждом из N опытов. Отметим, что количество опытов N должно быть достаточно большим. Уменьшить количество опытов можно за счет использования методов планирования экспериментов (см. следующую лекцию). Система нормальных уравнений, аналогично линейному случаю имеет вид (8.1). Как видим, эта система уравнений имеет упорядоченное строение и может быть легко составлено для любого количества факторов k. В этой системе из k+1 уравнений с k+1 неизвестными k+1 слагаемых в левой части каждого уравнения. В том случае, если используется модель в виде полинома выше первого порядка, нелинейные члены уравнения регрессии рассматриваются как самостоятельные переменные 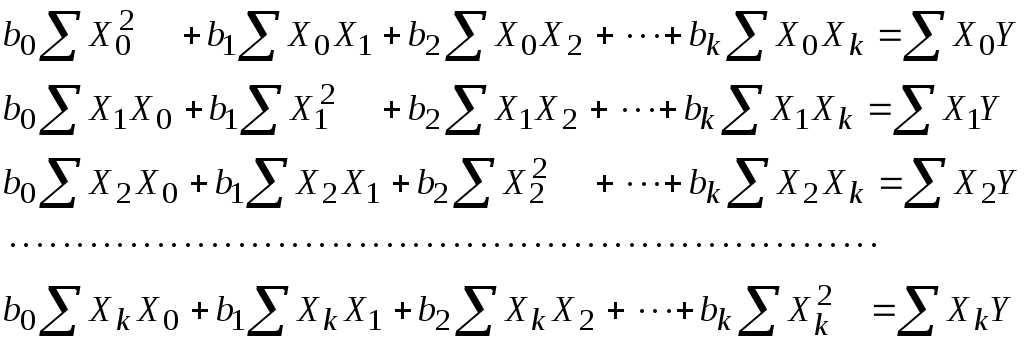  (8.1)Рассмотрим пример, когда k=2 и ищутся коэффициенты модели уравнения вида:  . (8.2)В качестве базовой берется модель: 1 2 3 4 5 6 <- номера коэффициентов  (3.3)Исходный статистический материал представлен в следующей таблице: 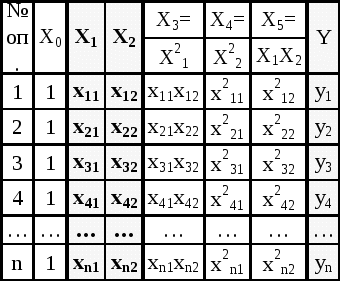 Здесь выделенная часть таблицы – реальный эксперимент, остальная часть таблицы заполняется путем вычислений. Например: 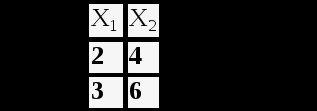 Система нормальных уравнений, аналогично предыдущему случаю имеет вид: 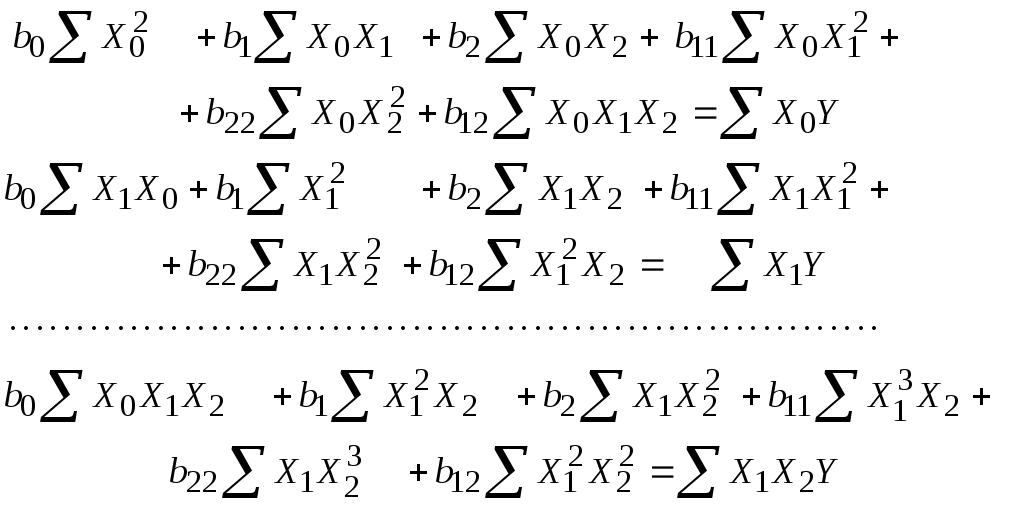 (8.4)Коэффициенты bi находятся решением этой системы, что гораздо проще делать в матричной форме, как мы увидим ниже (в лекции №10), для этого достаточно использовать выражение:  Основная литература Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е издание, перераб. и дополненное. -М.: Высшая школа, 2005. -327с. Дополнительная литература Гроп Д. Методы идентификации систем. - М.: Мир, 1979. Эйкхофф П. Основа идентификации систем управления. - М.: Мир, 1975. Лекция 9 Статические модели в форме управления регрессии и методы их определения (часть 3)Основы матричной алгебры (операции с матрицами) Матрица - математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение) между ним и другими подобными объектами. Обычно матрицы представляются двумерными (прямоугольными) таблицам. Использование матричного аппарата позволяет значительно упростить вычислительные операции с использованием линейных математических моделей. У каждого элемента матрицы есть два нижних индекса (aij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размера  ,» подразумевая, что в матрице m строк и n столбцов. В такой матрице индексы элементов удовлетворяют неравенствам  (если индексы отсчитываются от единицы) или  (если индексы отсчитываются от нуля).Операции над матрицами. Пусть aij - элементы матрицы A, а bij - элементы матрицы B. Линейные операции (это умножение на число, сложение и вычитание). Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен: bij = λaij Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: cij = aij + bij Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой: cij = aij - bij Примеры:   Нелинейные операции (это умножение матриц, возведение в степень, транспонирование, обращение). Умножение матриц (обозначение: AB, реже со знаком умножения  ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго, а именно: В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность 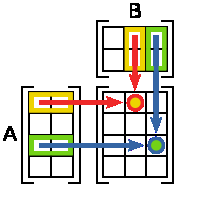, B -  , то размерность их произведения AB = C есть  . Схема этой процедуры показана на рисунке 3.1 Рисунок 9.1 – Схема умножения матриц Примеры умножения матриц: 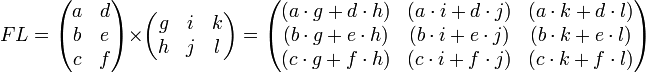    Возводить в степень можно только квадратные матрицы, непример: 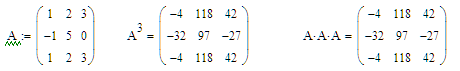 Транспонирование матрицы (обозначение: AT) — операция, при которой матрица отражается относительно главной диагонали, то есть:  Если A — матрица размера , то AT — матрица размера . Свойства операций над матрицами ассоциативность сложения: A + (B + C) = (A + B) + C. коммутативность сложения: A + B = B + A. ассоциативность умножения: A(BC) = (AB)C. Вообще говоря, умножение матриц не коммутативно:  Дистрибутивность умножения относительно сложения: A(B + C) = AB + AC; (B + C)A = BA + CA. Свойства операции транспонирования матриц: (AT)T = A; (AB)T = BTAT: (A−1)T = (AT)−1, (если обратная матрица A-1 существует); (A+ B)T = AT + BT; detA = detAT Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной. Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно: EA = AE = A. У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю.  Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A-1 такова, что если умножить матрицу на неё, то получится единичная матрица: AA−1 = E. Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности  на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю. У сингулярной матрицы определитель равен нулю или близок к нулю. Обычно это происходит, когда элементы матрицы значительно (на много порядков) отличаются друг от друга.Сингулярность матрицы иногда делает невозможность выполнять решение задчи регрессионного анализа и решения уравнений. Матрица как запись коэффициентов системы линейных уравнений. Систему из m уравнений с n неизвестными: 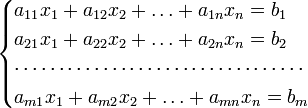 можно представить в матричном виде: 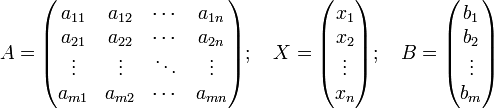 и тогда всю систему можно записать так: AX = B, где A имеет смысл таблицы коэффициентов aij системы уравнений. Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A-1, поскольку, умножив обе части уравнения на эту матрицу слева: A-1AX = A-1B A−1A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений: X = A-1B. Векторы. Нами будут использоваться понятие вектор в смысле - одномерная матрица, т.е. вектор столбец. Для удобства записи вектора в строчку иногда применяют запись вида BT= вместо записи B=. Для вектора справедливы все приведенные выше правила операций с матрицами, например:  Основная литература Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с. Построение математических моделей химико-технологических процессов. Под ред. Дудникова Е.Г. - Л.: Химия, 1970. –312 с. Дополнительная литература Гроп Д. Методы идентификации систем. - М.: Мир, 1979 Эйкхофф П. Основа идентификации систем управления. - М.: Мир, 1975. |