Лекц комплекс СМИОСУ 2017. Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление
 Скачать 4.07 Mb. Скачать 4.07 Mb.
|
Лекция 6 Оценка статистических показателей(часть2)Критерий Фишера (F-критерий, φ*-критерий, критерий наименьшей значимой разности) — апостериорный статистический критерий, используемый для сравнения дисперсий двух вариационных рядов, то есть для определения значимых различий между групповыми средними в установке дисперсионного анализа. 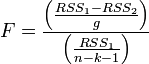 Критерий Фишера широко применяется в задачах статистического оценивания. Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта. Критерий оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект. Критерий Фишера. Используется у нас для проверки адекватности уравнения регрессии. Расчетное значение критерия Фишера определяют, как: 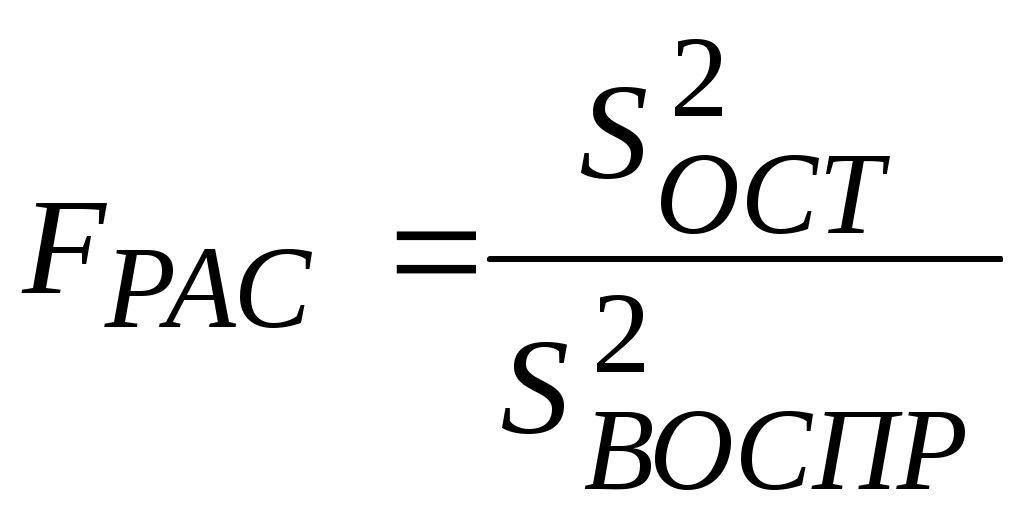 (6.1) (6.1) Оценка остаточной дисперсии (дисперсии адекватности) рассчитывают по формуле: 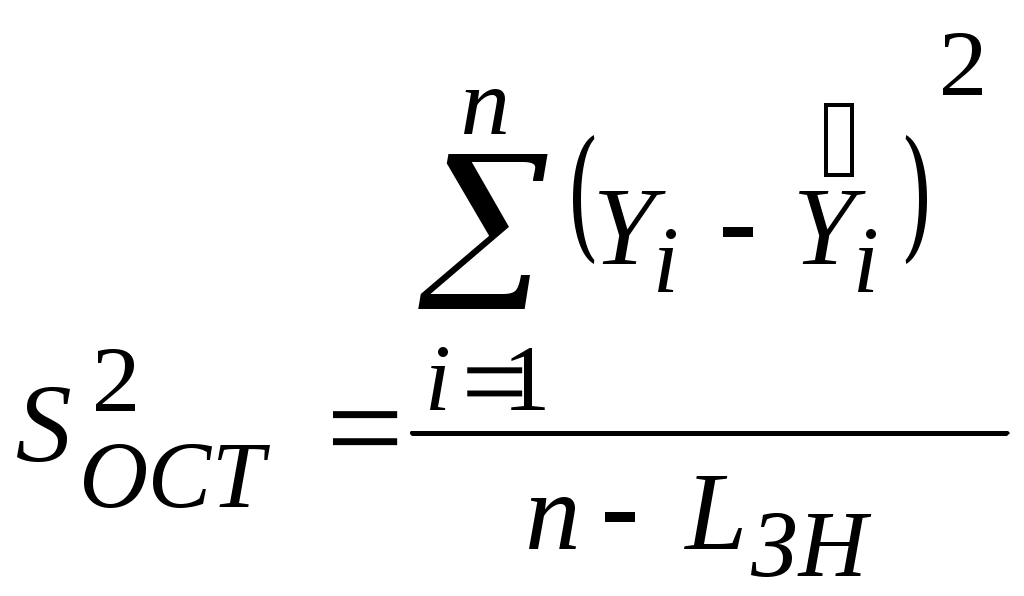 f1 = n – LЗН и f2 = n0 – 1. Обычно используют уровень значимости р=0,05. Выборочный коэффициент корреляции [См.1, стр.121]: 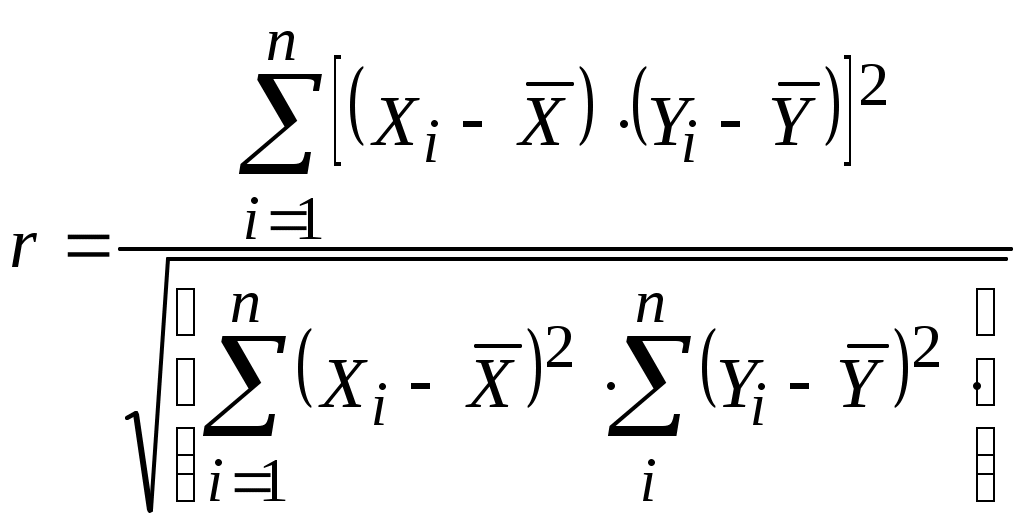 или или 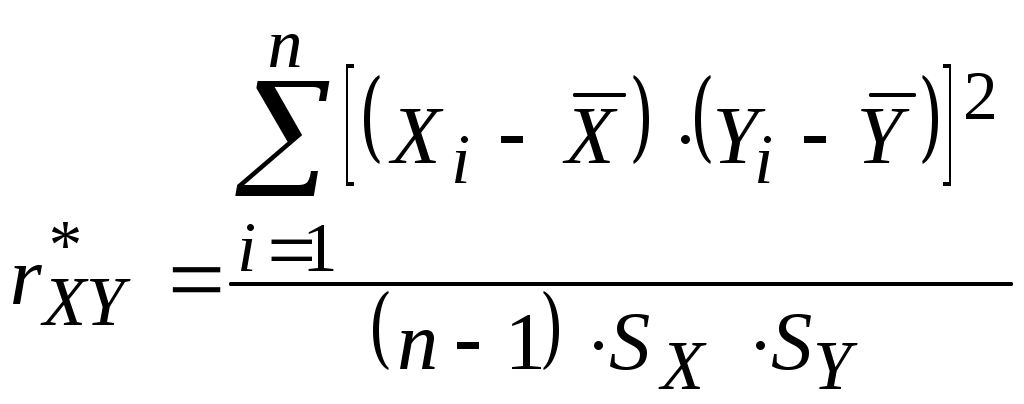 Рассмотрим пример на Mathcad, для данных приведенный в [1, стр.164].   Таким образом, адекватность полученных математических моделей статики может проверяться проверялась по критерию Фишера. Дополнительно для этого может быть использован более удобный т.н. критерии пригодности приближения [5] R-квадрат (коэффициент детерминации), используемый для оценки точности нелинейных моделей. Критерий R-квадрат может принимать значения только от нуля до единицы и чем ближе он к единице, тем лучше параметрическая модель приближает исходные данные. Коэффициент детерминации (R2) — это доля объяснённой дисперсии отклонений зависимой переменной от её среднего значения. Зависимая переменная объясняется (прогнозируется) с помощью функции от объясняющих переменных, в частном случае является квадратом коэффициента корреляции между зависимой переменной и её прогнозными значениями с помощью объясняющих переменных. Тогда можно сказать, что R2 показывает, какая доля дисперсии результативного признака объясняется влиянием объясняющих переменных. Формула для вычисления коэффициента детерминации: где yi — наблюдаемое значение зависимой переменной, а fi — значение зависимой переменной предсказанное по уравнению регрессии -среднее арифметическое зависимой переменной. Для его определения вначале вычисляется критерий SSE (Sum of squares due to error) - сумма квадратов ошибок по формуле: где wk - веса (у нас они не заданы, и считаются равными единице); yk - экспериментальные (исходные) значения данных для каждого опыта; n - количество экспериментальных значений (например, n=20). Критерий R-квадрат (обозначенный ниже как R) определяется как отношение суммы квадратов относительно регрессии SSR к полной сумме квадратов (SST), т.е.: где Близость полученных значений критерия R-квадрат к единице говорит о высокой точности описания эксперимента, например, выражением вида (2.2). Обычно приемлемыми для практики считают значения критерия R-квадрат выше 0,9. Данный показатель является статистической мерой согласия, с помощью которой можно определить, насколько уравнение регрессии соответствует реальным данным. Коэффициент детерминации изменяется в диапазоне от 0 до 1. Если он равен 0, это означает, что связь между переменными регрессионной модели отсутствует, и вместо нее для оценки значения выходной переменной можно с таким же успехом использовать простое среднее ее наблюдаемых значений. Напротив, если коэффициент детерминации равен 1, это соответствует идеальной модели, когда все точки наблюдений лежат точно на линии регрессии, т.е. сумма квадратов их отклонений равна 0. На практике, если коэффициент детерминации близок к 1, это указывает на то, что модель работает очень хорошо (имеет высокую значимость), а если к 0, то это означает низкую значимость модели, когда входная переменная плохо "объясняет" поведение выходной, т.е. линейная зависимость между ними отсутствует. Очевидно, что такая модель будет иметь низкую эффективность. Кроме того, о точности аппроксимации результатов эксперимента можно дополнительно судить по значениям суммарных абсолютных и относительных ошибок и анализируя графики сравнения расчетных и экспериментально найденных значений выхода для каждого опыта. Иногда показателям тесноты связи можно дать качественную оценку (шкала Чеддока):
Функциональная связь возникает при значении равном 1, а отсутствие связи — 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50 %. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение. Основная литература Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е издание, перераб. и дополненное. -М.: Высшая школа, 2005. -327с. Советов Б.Я., Яковлев С.А. Моделирование систем. – М.: Высшая школа. 2001 Дополнительная литература Гроп Д. Методы идентификации систем. - М.: Мир, 1979. Эйкхофф П. Основа идентификации систем управления. - М.: Мир, 1975. |
