Конспект лекций по дисциплине Элементы высшей математики

• Название: Конспект лекций по дисциплине Элементы высшей математики
• Дата: 30.06.2022
• Размер: 2.87 Mb.
• Имя файла: konspekt_lektsiy_po_vysshey_matematike.doc
• Тип: Конспект лекций; #620974
• страница: 5 из 5

D = 36 – 32 = 4; D = 64 – 48 = 16;

x₁ = (6 + 2)/2 = 4; x₁ = (8 + 4)/2 = 6;

x₂ = (6 – 2)/2 = 2 ; x₂ = (8 – 4)/2 = 2;

Тогда

Пример. Найти предел.

домножим числитель и знаменатель дроби на сопряженное выражение: =

= .

Пример. Найти предел.



Пример. Найти предел .

Разложим числитель и знаменатель на множители.

x² – 3x + 2 = (x – 1)(x – 2)

x³ – 6x² + 11x – 6 = (x – 1)(x – 2)(x – 3), т.к.

x ³ – 6x² + 11x – 6 x - 1

x³ – x² x² – 5x + 6

- 5x² + 11x

- 5x² + 5x

6x - 6

6x - 6 0
x² – 5x + 6 = (x – 2)(x – 3)

Тогда

Пример. Найти предел.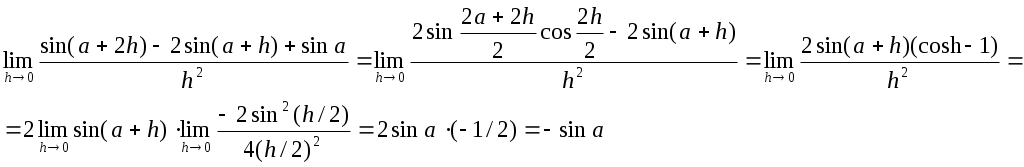



Для самостоятельного решения:

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   

8) - не определен.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. 
   Дайте определение предела функции точке.
   
2. 
   Дайте определение предела функции на бесконечности.
   
3. 
   Что такое односторонние пределы функции?
   
4. 
   Сформулируйте основные теоремы о пределах функций.
   
5. 
   Что такое первый, второй и третий замечательные пределы?
   
6. 
   Дайте определение бесконечно малой функции.
   
7. 
   Сформулируйте основные свойства бесконечно малых функций.
   
8. 
   Сформулируйте принцип эквивалентности бесконечно малых функций.
   
9. 
   Дайте определение бесконечно большой функции.
   
10. 
    Сформулируйте основные свойства бесконечно больших функций.
    
11. 
    В чем заключается связь бесконечно больших и бесконечно малых функций?
    

Определение.'>Лекция № 9. Непрерывность функции и ее разрывы.
9.1. Непрерывность функции в точке.
Определение. Функция f(x), определенная в окрестности некоторой точки х₀, называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т.е.



Тот же факт можно записать иначе:

Определение. Если функция f(x) определена в некоторой окрестности точки х₀, но не является непрерывной в самой точке х₀, то она называется разрывной функцией, а точка х₀ – точкой разрыва.

Пример непрерывной функции: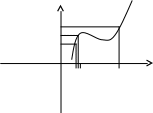
y
f(x₀)+

f(x₀)

f(x₀)-
0 x₀- x₀ x₀+ x


П 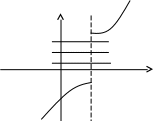ример разрывной функции:
y
f(x₀)+

f(x₀)

f(x₀)-

x₀ x
Определение. Функция f(x) называется непрерывной в точке х₀, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию


верно неравенство .

Определение. Функция f(x) называется непрерывной в точке х = х₀, если приращение функции в точке х₀ является бесконечно малой величиной.

f(x) = f(x₀) + (x)

где (х) – бесконечно малая при хх₀.
9.2. Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х₀ функций – есть функция, непрерывная в точке х₀.

2) Частное двух непрерывных функций – есть непрерывная функция при условии, что g(x) не равна нулю в точке х₀.

3) Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х₀, то функция v = g(f(x)) – тоже непрерывная функция в этой точке.

Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.
9.3. Непрерывность некоторых элементарных функций.
1) Функция f(x) = C, C = const – непрерывная функция на всей области определения.

2) Рациональная функц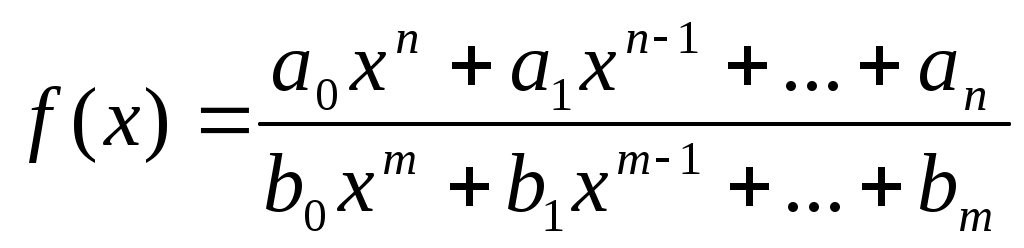ия непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.

3) Тригонометрические функции непрерывны на своей области определения.

Докажем свойство 3 для функции y = sinx.

Запишем приращение функции y = sin(x + x) – sinx, или после преобразования:





Действительно, имеется предел произведения двух функций и . При этом функция косинус – ограниченная функция при х0 , а т.к.

предел функции синус , то она является бесконечно малой при х0.

Таким образом, имеется произведение ограниченной функции на бесконечно малую, следовательно это произведение, т.е. функция у – бесконечно малая. В соответствии с рассмотренными выше определениями, функция у = sinx – непрерывная функция для любого значения х = х₀ из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.

Аналогично можно доказать непрерывность остальных тригонометрических функций на всей области определения.

Вообще следует заметить, что все основные элементарные функции непрерывны на всей своей области определения.
9.4. Точки разрыва и их классификация.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х₀, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х₀ является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

Если односторонний предел (см. выше) , то функция называется непрерывной справа.



х₀


Если односторонний предел (см. выше) , то функция называется непрерывной слева.


х₀


Определение. Точка х₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х₀ или не является непрерывной в этой точке.

Определение. Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.



Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х₀, достаточно того, что она определена слева и справа от нее.

Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.

Определение. Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)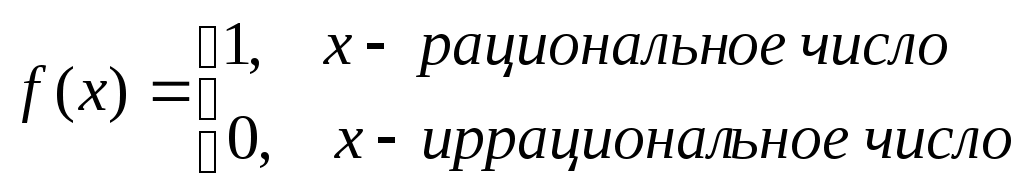



не является непрерывной в любой точке х₀.

Пример. Функция f(x) = имеет в точке х₀ = 0 точку разрыва 2 – го рода, т.к.

.



Пример. f(x) =

Функция не определена в точке х = 0, но имеет в ней конечный предел 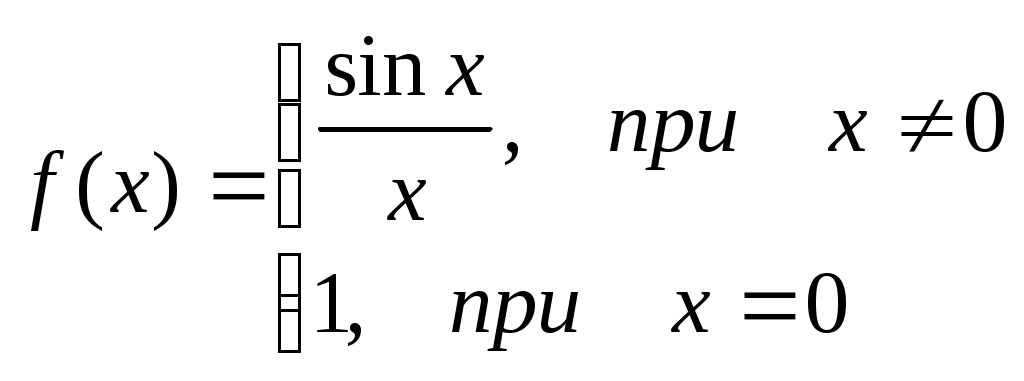, т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:



График этой функции: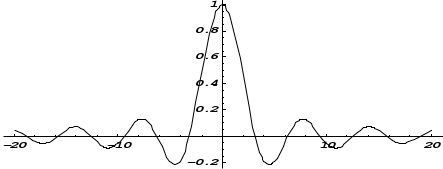

Пример. f(x) = =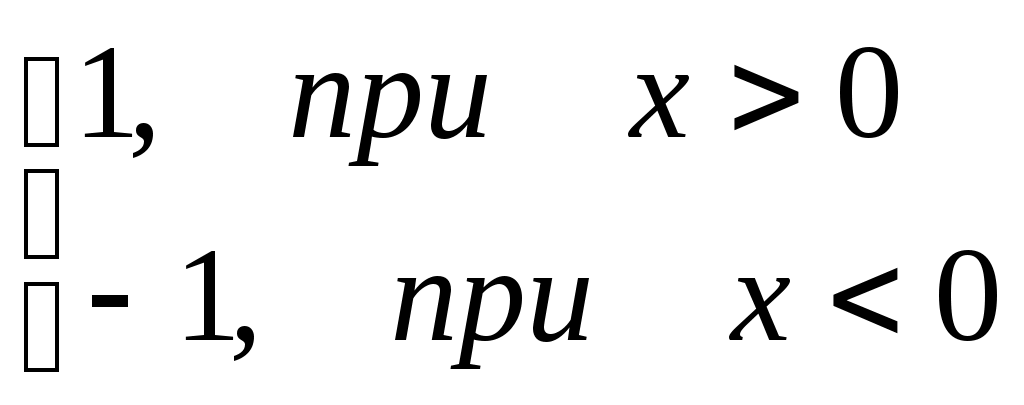
y

1

0 x
-1

Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.

Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.
9.5. Непрерывность функции на интервале и на отрезке.
Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).

При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.

Свойства функций, непрерывных на отрезке.

Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M  f(x)  M.

Доказательство этого свойства основано на том, что функция, непрерывная в точке х₀, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х₀, то образуется некоторая окрестность точки х₀.

Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.

Т.е. существуют такие значения х₁ и х₂, что f(x₁) = m, f(x₂) = M, причем

m  f(x)  M

Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).

Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.

Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.

Свойство 4: Если функция f(x) непрерывна в точке х = х₀, то существует некоторая окрестность точки х₀, в которой функция сохраняет знак.

Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.

Т.е. если sign(f(a))  sign(f(b)), то  х₀: f(x₀) = 0.

Определение. Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого >0 существует >0 такое, что для любых точек х₁[a,b] и x₂[a,b] таких, что

х₂ – х₁< 

верно неравенство f(x₂) – f(x₁) < 

Отличие равномерной непрерывности от “обычной” в том, что для любого  существует свое , не зависящее от х, а при “обычной” непрерывности  зависит от  и х.

Свойство 6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем.

(Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)

Пример.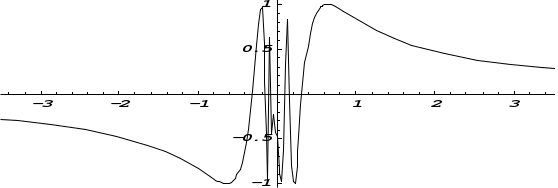



Функция непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т.к. существует такое число >0 такое, что существуют значения х₁ и х₂ такие, чтоf(x₁) – f(x₂)>,  - любое число при условии, что х₁ и х₂ близки к нулю.

Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.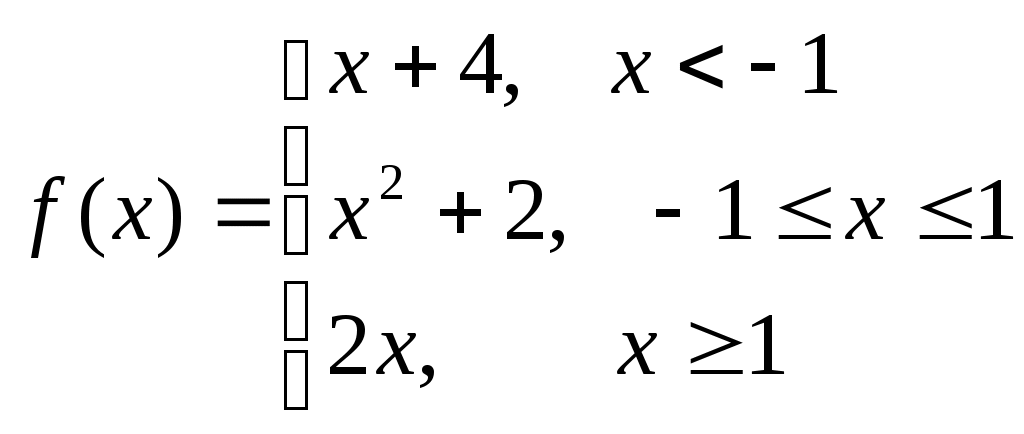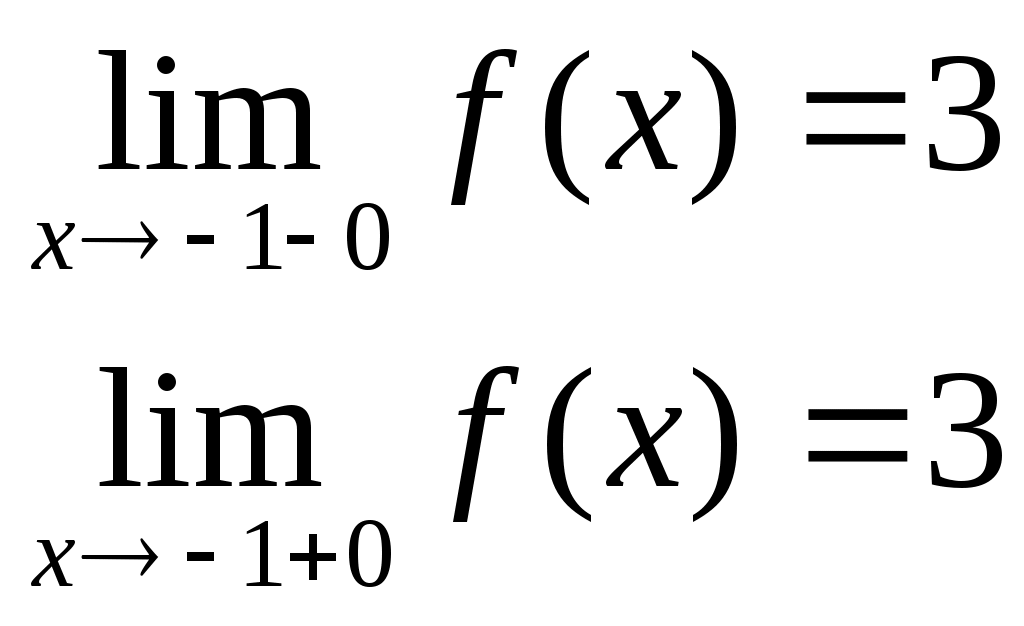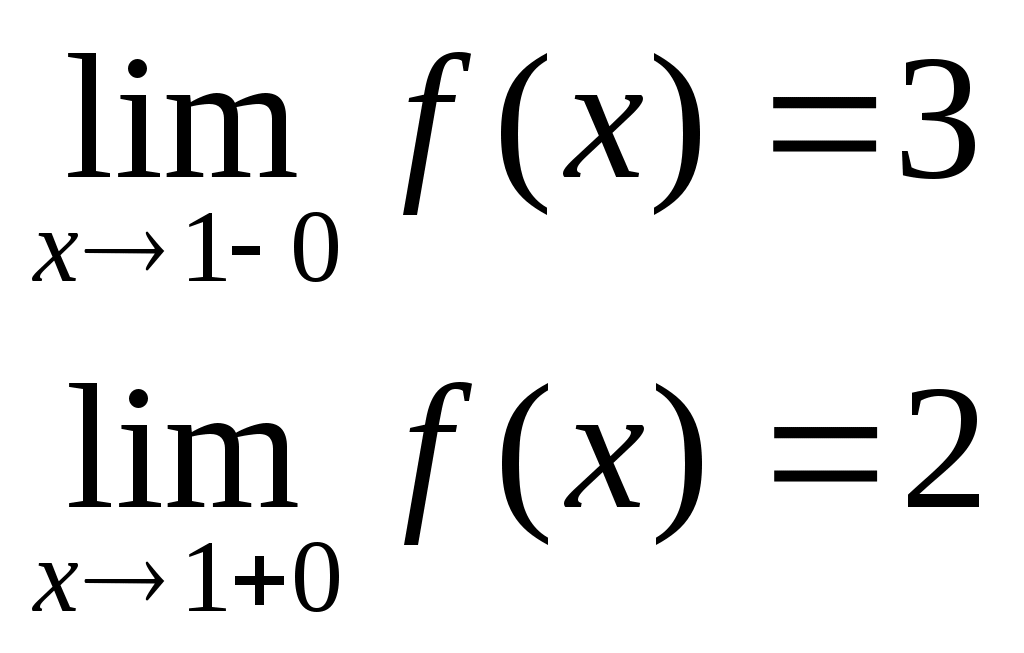





в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода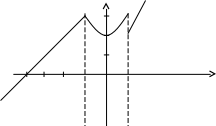


у

3
2

-4 -1 0 1 х

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.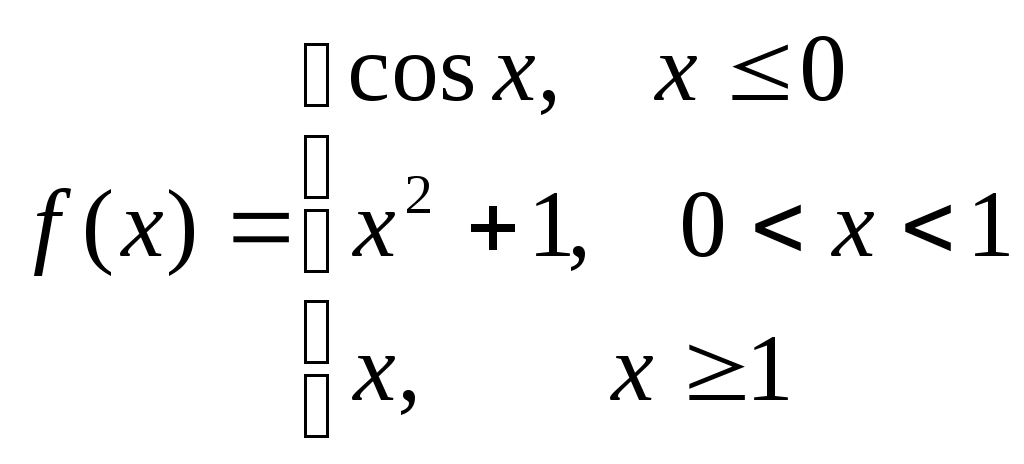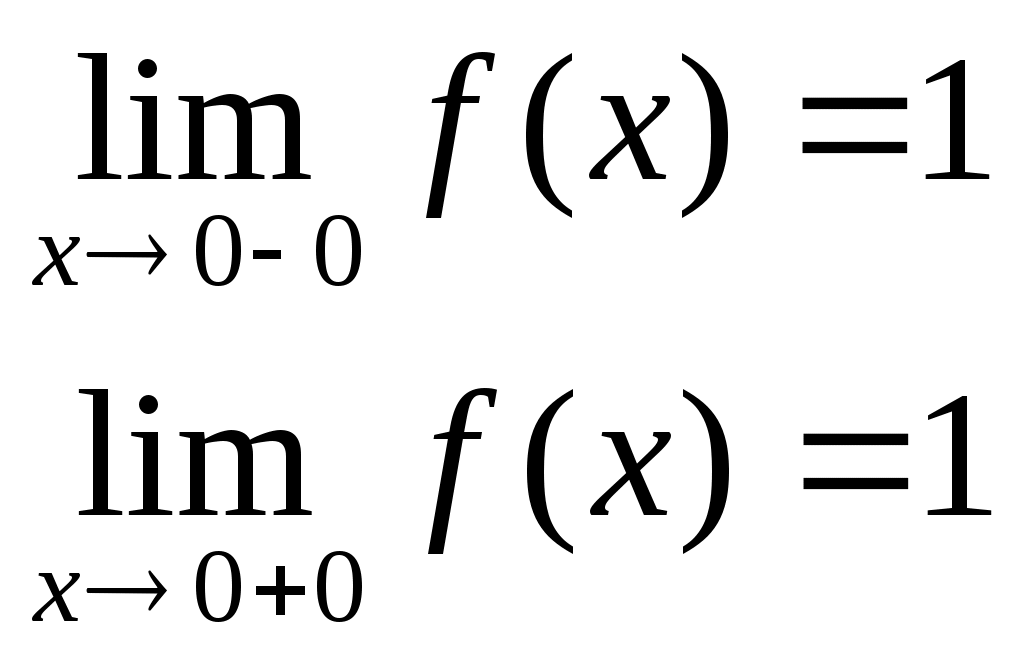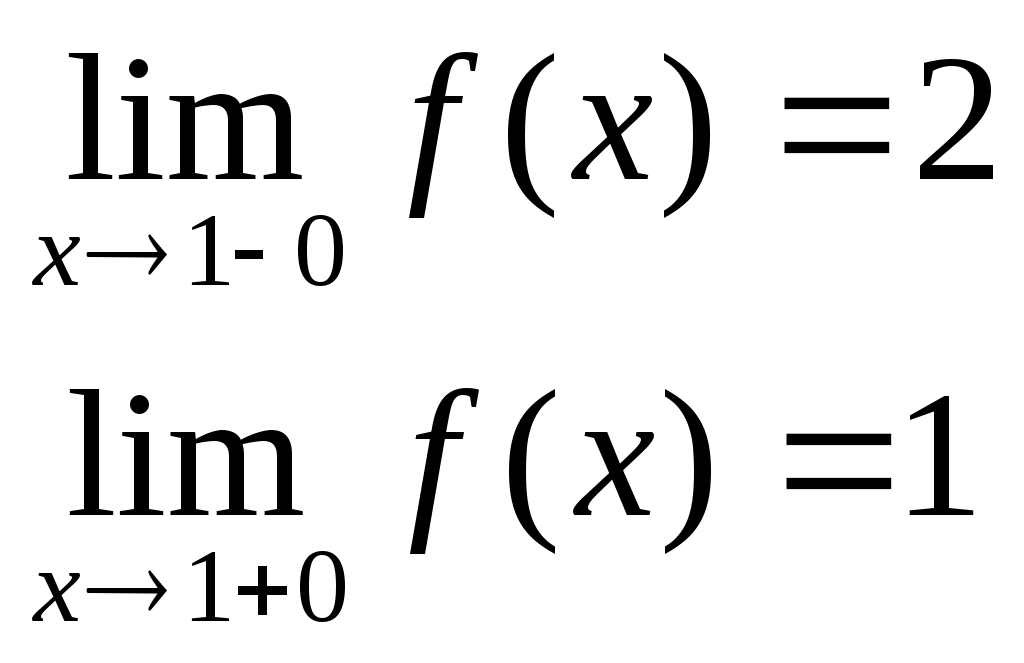





в точке х = 0 функция непрерывна, в точке х = 1 точка разрыва 1 – го рода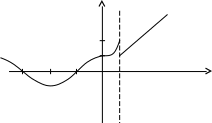




у


2

1
- -/2 0 1 x

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. 
   Дайте определение непрерывности функции в точке.
   
2. 
   Приведите примеры функций непрерывных в точке.
   
3. 
   Дайте определение непрерывности функции на интервале.
   
4. 
   Что такое точка разрыва? Точки разрыва первого и второго рода.
   
5. 
   Приведите примеры точек разрыва первого и второго рода.
   
6. 
   Сформулируйте основные свойства непрерывных функций.
   
7. 
   Приведите примеры непрерывности элементарных функций.
   

Литература

1. 
   Беклемищева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре. – М., 1987.
   
2. 
   Н.В.Богомолов Практические занятия по математике. – М., 1983.
   
3. 
   Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. – М., 1986.
   
4. 
   Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М., 1980.
   
5. 
   Демидович Б.П. Сборник задач и упражнений по математическому анализу. – М., 1989.
   
6. 
   Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (2 книги) – М., 2004.
   
7. 
   Кудрявцев Л.Д. Краткий курс математического анализа: Учебник для вузов. – М., 1989.
   
8. 
   Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. – М., 2003.
   
9. 
   Марков Л.Н., Размыслович Г.П. Высшая математика: Учебник для вузов. – М., 1999.
   
10. 
    Пискунов Н.С. Дифференциальное и интегральное исчисления. Для вузов. Т.I, 2. – М., 1985.
    
11. 
    Подольский В.А., Суходский А.М., Мироненко Е.С. Сборник задач по математике. – М., 1999.
    
12. 
    Фихтенгольц Г.М. Основы математического анализа. Т.I, 2. – М., 1968.