конспект-метрология. Конспект лекций по дисциплине Метрология, стандартизация, сертификация Казань 2012
 Скачать 2.75 Mb.
|
Таблица 1.4
2. Если в тех же документах случайные составляющие погрешности результата наблюдения представлены доверительными границами i(P) при одной и той же доверительной вероятности P, то доверительную границу случайной погрешности результата измерения с однократным наблюдением при доверительной вероятности вычисляют по формуле 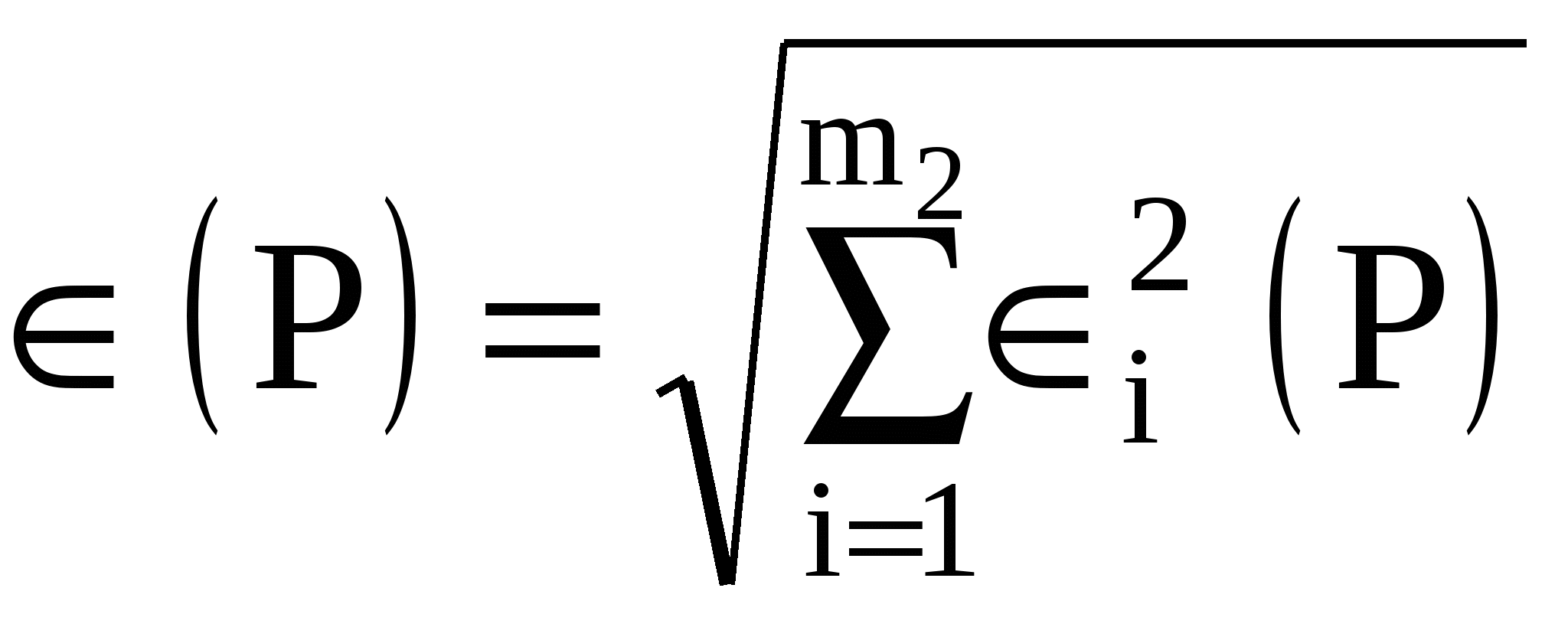 .3. Если случайные составляющие погрешности результата наблюдения определяют предварительно в реальных рабочих условиях экспериментальными методами при числе наблюденийи ni <30, то: 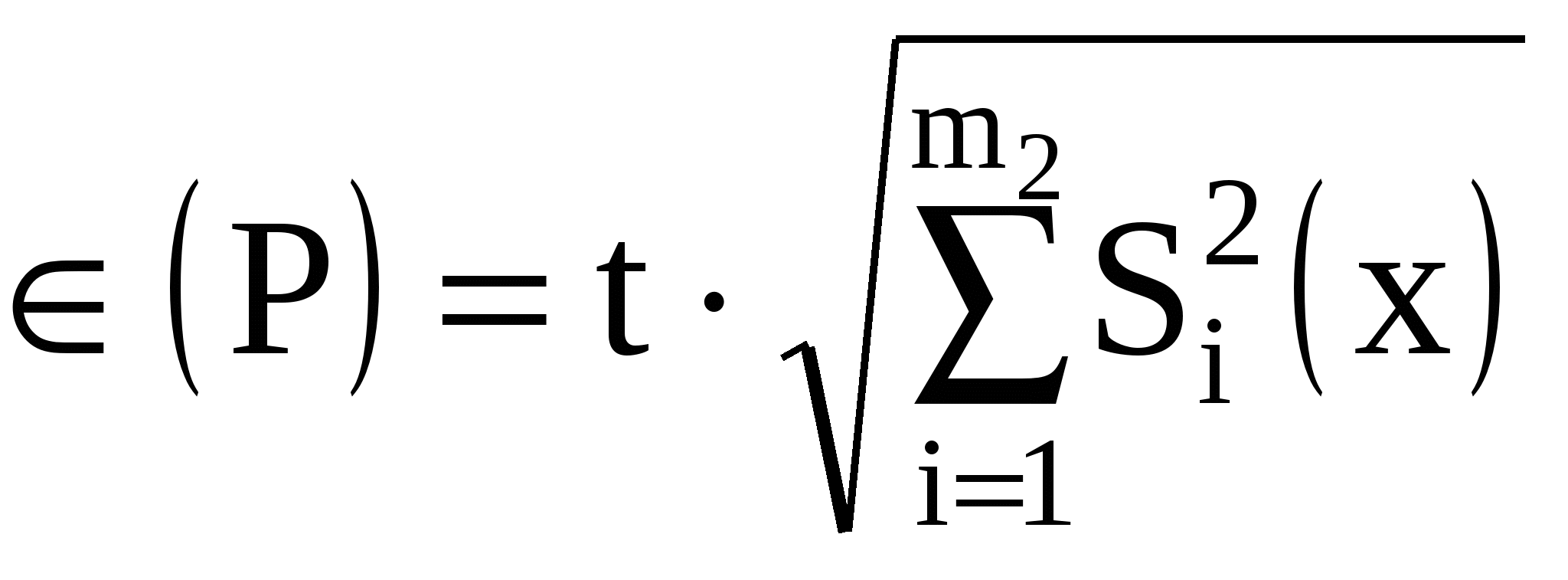 ,где t - коэффициент Стьюдента, соответствующий наименьшему числу наблюдений nmin из всех ni, можно найти в любом справочнике по теории вероятностей; S(x) - оценки СКО случайных составляющих погрешности результата наблюдения, определяемых по формуле (1.16). Если в эксперименте невозможно или нецелесообразно определить СКО составляющих случайной погрешности и определено сразу суммарное СКО, то в формуле (1.11) m2 = 1. 4. Если случайные составляющие погрешности результата наблюдений представлены доверительными границами (Pi), соответствующими разным вероятностям Рi, то сначала определяют СКО результата измерения с однократным наблюдением по формуле  ,где zPi/2 - значения функции Лапласа. Затем вычисляют (P) по формуле (1.10). Для суммирования систематической и случайной составляющих погрешностей рекомендуется следующий способ: Если (P)/S(x) < 0,8, (1.12) то НСП (P) пренебрегают и окончательно принимают (P) за погрешность результата измерения (P) при доверительной вероятности Р. Если(P)/S(x) 0,8, (1.13)то пренебрегают случайной погрешностью и принимают (P) = (P).Если 0,8 (P)/S(x) 8, то доверительную границу погрешности результата измерений вычисляют по формуле  , (1.14)где K() =  ;  .2. Измерения с многократными наблюдениями. Обработку результатов в этом случае рекомендуется начать с проверки на отсутствие промахов (грубых погрешностей). Промах — это результат xп отдельного наблюдения, входящего в ряд из n наблюдений, который для данных условий измерений резко отличается от остальных результатов этого ряда. Если оператор в ходе измерения обнаруживает такой результат и достоверно находит его причину, он вправе его отбросить и провести (при необходимости) дополнительное наблюдение взамен отброшенного. При обработке уже имеющихся результатов наблюдений произвольно отбрасывать отдельные результаты нельзя, так как это может привести к фиктивному повышению точности результата измерения. Поэтому применяют следующую процедуру. Вычисляют среднее арифметическое  результатов наблюдений хi по формуле . (1.15)Затем вычисляют оценку СКО результата наблюдения как  . (1.16)Находят отклонение vп предполагаемого промаха xп от :vп = xп -  .По числу всех наблюдений n (включая xп) и принятому для измерения значению Р (обычно 0,95) по любому справочнику по теории вероятностей находят z(P,n) - нормированное выборочное отклонение нормального распределения. Если vп < zS(x), то наблюдение xп не является промахом; если vп zS(x), то xп — промах, подлежащий исключению. После исключения xп повторяют процедуру определения и S(x) для оставшегося ряда результатов наблюдений и проверки на промах наибольшего из оставшегося ряда отклонений от нового значениям (вычисленного исходя из n - 1).За результат измерения принимают среднее арифметическое по формуле (1.15) результатов наблюдений хi. Погрешность содержит случайную и систематическую составляющие. Случайную составляющую, характеризуемую СКО результата измерения, оценивают по формуле .В предположении принадлежности результатов наблюдений хi к нормальному распределению находят доверительные границы случайной погрешности результата измерения при доверительной вероятности Р по формуле (P) = t(P,n) S( ) , (1.17)где t - коэффициент Стьюдента. Доверительные границы (Р) НСП результата измерения с многократными наблюдениями определяют точно так же, как и при измерении с однократным наблюдением — по формулам (1.9) или (1.10). Суммирование систематической и случайной составляющих погрешности результата измерения при вычислении (Р) рекомендуется осуществлять с использованием критериев и формул (1.12 – 1.14), в которых при этом S(x) заменяется на S( ) = S(x)/ .3. Косвенные измерения. Значение измеряемой величины А находят по результатам измерений аргументов а1, . . . , аi,…am, связанных с искомой величиной уравнением  f(a1,….ai….am). (1.18)Вид функции f определяется при установлении модели ОИ. Косвенное измерение при линейной зависимости. Искомая величина А связана с m измеряемыми аргументами уравнением  ,где bi - постоянные коэффициенты. Предполагается, что корреляция между погрешностями измерений ai отсутствует. Результат измерения А вычисляют по формуле  ,где  — результат измерения ai с введенными поправками. Оценку СКО результата измерения S(A) вычисляют но формуле ,где  — оценка СКО результата измерений .Доверительные границы (Р) случайной погрешности  при нормальном распределении погрешностей  , (1.19)где t(P,nэф) — коэффициент Стьюдента, соответствующий доверительной вероятности Р (обычно 0,95, в исключительных случаях 0,99) и эффективному числу наблюдений nэф , вычисляемому по формуле 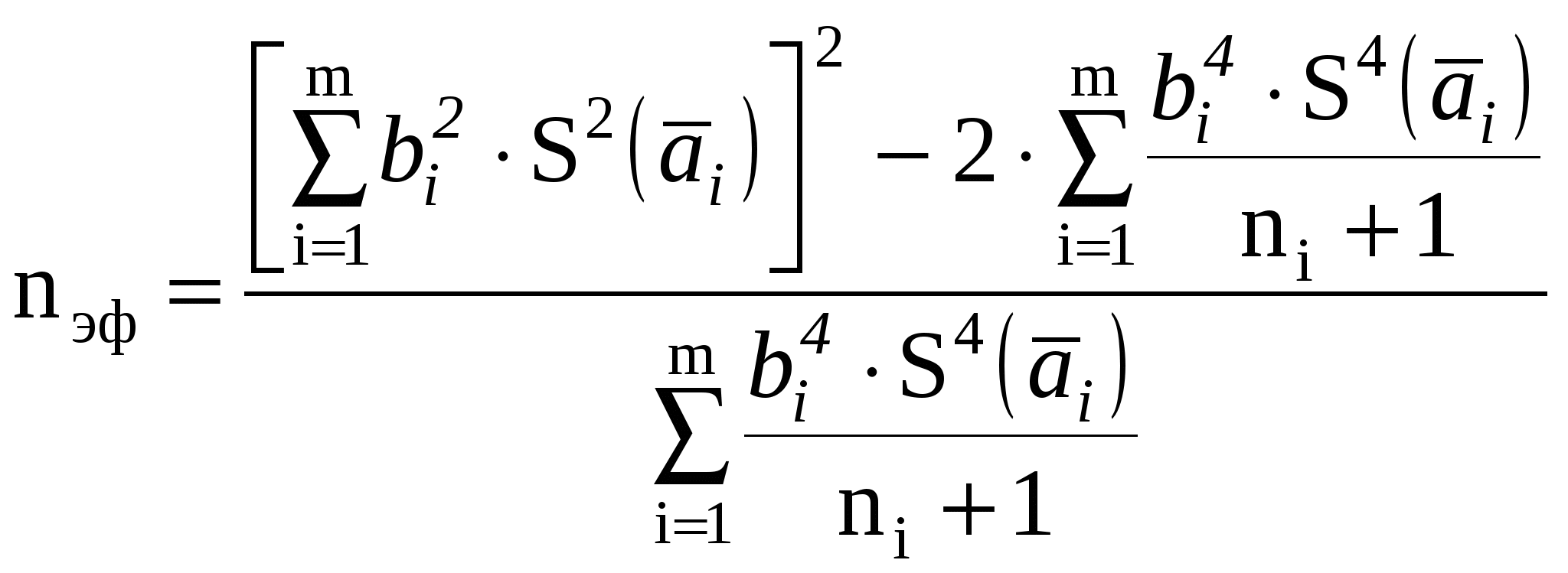 ,где ni —число наблюдений при измерении аi. Доверительные границы (Р) НСП результата такого измерения, сумму (Р) и (Р) для получения окончательного значения (Р) рекомендуется вычислять с использованием критериев и формул (1.9), (1.10), (1.12) – (1.14), в которых m1, i, и S(x) заменяются, соответственно, на m, bii, и S( ).Косвенные измерения при нелинейной зависимости. При некоррелированных погрешностях измерений аi используется метод линеаризации путем разложения функции f(а1, . . . , am) в ряд Тейлора, то есть f(а1, . . . , am) =  ,где  - отклонение отдельного результата наблюдения аi от  ; R - остаточный член.Метод линеаризации допустим, если приращение функции f можно заменить ее полным дифференциалом. Остаточным членом 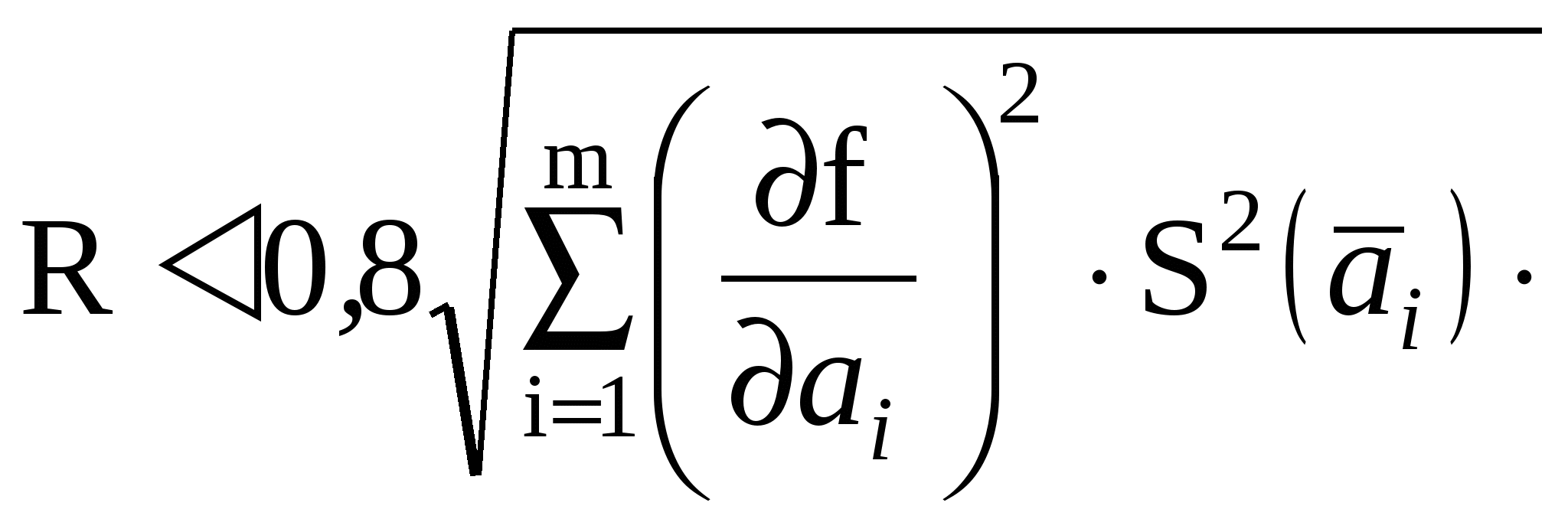 пренебрегают, если  ,где — оценка СКО случайных погрешностей результата измерения . При этом отклонения должны быть взяты из возможных значений погрешностей и такими, чтобы они максимизировали R.Результат измерения вычисляют по формуле = f( .Оценку СКО случайной составляющей погрешности результата такого косвенного измерения S( 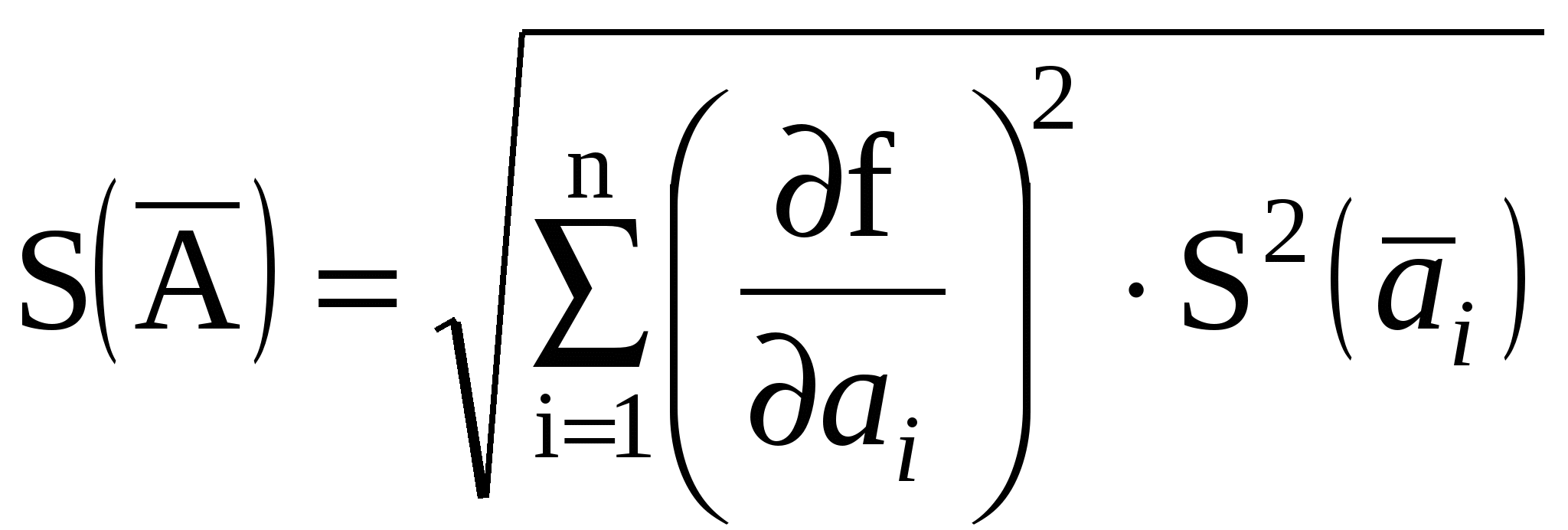) вычисляют по формуле ,а (Р) — по формуле (1.19). Значение nэф , границы НСП (Р) и погрешность (Р) результата косвенного измерения при нелинейной зависимости вычисляют так же, как и при линейной зависимости, но с заменой коэффициентов bi на f/ai Метод приведения (для косвенных измерений с нелинейной зависимостью) применяется при неизвестных распределениях погрешностей измерений ai и при корреляции между погрешностями ai для получения результата косвенного измерения и определения его погрешности. При этом предполагается наличие ряда n результатов наблюдений aij измеряемых аргументов аi. Сочетания aij, полученных в j-м эксперименте подставляют в формулу (1.18) и вычисляют ряд значений Aj измеряемой величины А. Результат измерения вычисляют по формуле  .Оценку СКО S( ) - случайной составляющей погрешности -вычисляют по формуле ,а (Р) - по формуле (3.17). Границы НСП (Р) и погрешность (Р) результата измерения определяют описанными выше способами для нелинейной зависимости.Выбор измерительных средств по допустимой погрешности измерения При выборе измерительных средств и методов контроля изделий учитывают совокупность метрологических, эксплуатационных и экономических показателей. К метрологическим показателям относятся: допустимая погрешность измерительного прибора-инструмента; цена деления шкалы; порог чувствительности; пределы измерения и др. К эксплуатационным и экономическим показателям относятся: стоимость и надежность измерительных средств; продолжительность работы (до ремонта); время, затрачиваемое на настройку и процесс измерения; масса, габаритные размеры и рабочая нагрузка. Выбор измерительных средств для контроля размеров На рис. 1.5 показаны кривые распределения размеров деталей (утех) и погрешностей измерения (умет) с центрами, совпадающими с границами допуска. В результате наложения кривых умет и утех происходит искажение кривой распределения у(тех, мет), появляются области вероятностей т и п, обусловливающие выход размера за границу допуска на величину с. Таким образом, чем точнее технологический процесс (меньше отношение /мет), тем меньше неправильно принятых деталей по сравнению с неправильно забракованными. Решающим фактором является допускаемая погрешность измерительного средства, что вытекает из стандартизованного определения действительного размера как и размера, получаемого в результате измерения с допустимой погрешностью. Допускаемые погрешности измерения изм при приёмочном контроле на линейные размеры до 500 мм устанавливаются ГОСТом 8.051, которые составляют 35-20% от допуска на изготовление детали IT. По этому стандарту предусмотрены наибольшие допускаемые погрешности измерения, включающие погрешности от средств измерений, установочных мер, температурных деформаций, измерительного усилия, базирования детали. Допускаемая погрешность измерения изм состоит из случайной и неучтённой систематической составляющих погрешности. При этом случайная составляющая погрешности принимается равной 2 и не должна превышать 0,6 от погрешности измерения изм . В ГОСТ 8.051 погрешность задана для однократного наблюдения. Случайная составляющая погрешности может быть значительно уменьшена за счёт многократных наблюдений, при которых она уменьшается в раз, где n - число наблюдений. При этом за действительный размер принимается среднеарифметическое из серии проведённых наблюдений.При арбитражной перепроверке деталей погрешность измерения не должна превышать 30% предела погрешности, допускаемой при приёмке. Значения допустимой погрешности измерения изм на угловые размеры установлены по ГОСТ 8.050 - 73. 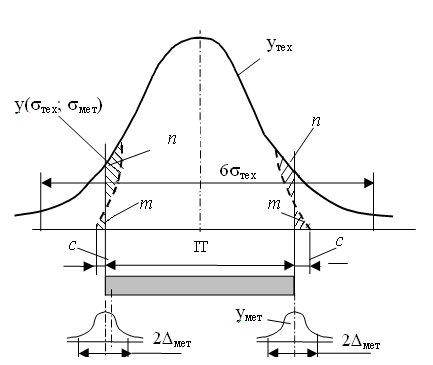 Рис.1.5. Кривые распределения контролируемых параметров, построенные с учетом погрешностей измерения Разрешается увеличение допустимой погрешности измерения, указанной в ГОСТ 8.051–81 и ГОСТ 8.050-73, при уменьшении допуска размера, учитывающего это увеличение, а также в случае разделения изделий на размерные группы для селективной сборки. Установленные стандартом погрешности измерения являются наибольшими, которые можно допустить при  измерении: они включают в себя случайные и неучтенные систематические погрешности измерения, все составляющие, зависящие от измерительных средств, установочных мер, температурных деформаций, базирования и т. д.Случайная погрешность измерения не должна превышать 0,6 от допустимой погрешности измерения и принимается равной 2, где -значение стандартного погрешности измерения. При допусках, не соответствующих значениям, указанным в ГОСТ 8.051 – 81 и ГОСТ 8.050 - 73, допустимую погрешность выбирают по ближайшему меньшему значению допуска для соответствующего размера. Влияние погрешностей измерения при приемочном контроле по линейным размерам оценивается параметрами: т—часть измеренных деталей, имеющих размеры, выходящие за предельные размеры, принята в числе годных (неправильно принятые); п — часть деталей, имеющих размеры, не превышающие предельных размеров, забракованы (неправильно забракованные); с—вероятностная предельная величина выхода размера за предельные размеры у неправильно принятых деталей. Значения параметров т, п, с при распределении контролируемых размеров по нормальному закону приведены на рис. 1,6 и 1.7. 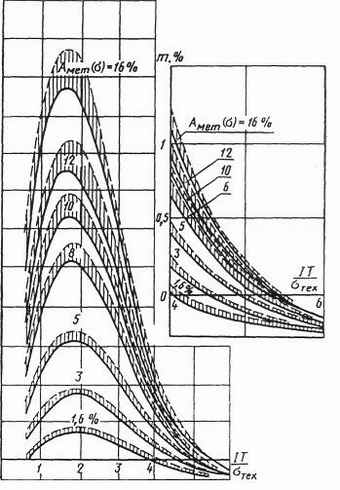 Сплошные линии соответствуют распреде-лению погрешности изме-рения по нормальному закону, а пунктирные - по закону равной вероят-ности. При неизвестном законе распределения погрешнос-ти измерения для парамет-ров т, п и с рекомендуется принимать средние их значения, определенных по сплошной и пунктир-ной линиям. Параметры m и с на графиках определены с доверительной вероят-ностью 0,9973. Для определения т с другой доверительной вероятностью необходимо сместить начало коорди-нат по оси ординат. Рис. 1.6. График для определения параметра m Кривые графиков (сплошные и пунктирные) соответствуют определенному значению относительной погрешности измерения, равной  ,где — сратнадтное отклонение погрешности измерения; IТ—допуск контролируемого размера. При определении параметров т, п и с рекомендуется принимать Амет( ) = 16 % для квалитетов 2—7, Амет( ) =12 % - для квалитетов 8, 9, Амет( ) =10 % - для квалитетов 10 и грубее.  Рис. 1.7. График для определения параметра c П Рис. 3.5. График для определения параметра n араметры т, п и с приведены на графиках в зависимости от значения IT/тех , где тех — срандартное отклонение погрешности изготовления. Параметры m, n и с даны при симметричном расположении поля допуска относительно центра группирования контролируемых деталей. Для определяется m, n и с при совместном влиянии систематической и случайной погрешностей изготовления пользуются теми же графиками, но вместо значения IT/тех принимается для одной границы  , а для другой -  , где Т — систематическая погрешность изготовления. При определении параметров m и n для каждой границы берется половина получаемых значений. Возможные предельные значения параметров т, п и с/IТ, соответствующие экстремальным значениям кривых (на рис. 1.5 – 1.7), приведены в табл.1.5. |