конспект-метрология. Конспект лекций по дисциплине Метрология, стандартизация, сертификация Казань 2012
 Скачать 2.75 Mb.
|
Законы распределения случайных величинВ метрологии при измерениях все наблюдаемые величины являются случайными и могут иметь самые различные законы распределения. Однако наиболее распространенными при обработке результатов наблюдений являются нормальный закон Гаусса и закон распределения Стьюдента, при разработке цифровых систем приборов используется квантование сигналов, в котором применяется треугольный и равномерный законы распределения, при измерении природных явлений, применяя теорию массового обслуживания, используется биномиальное распределение и т.п. Мы опишем только наиболее распространенные, отсылая к специальной литературе по теории вероятности и математической статистике (ГОСТ Р 50779.10-2000 (ИСО 3534.1-93)). Нормальное распределение Гаусса. Закон нормальное распределение Гаусса занимает особое положение в теории вероятности, математической статистике и теории обработки результатов измерений. Он широко применяется в физике. Этому закону распределения подчиняются многие природные явления и процессы. Он является также предельным – к нему стремятся многие другие законы распределения при возрастании числа измерений. Плотность распределения случайной величины при нормальном распределении Гаусса выражается в виде:  где   - математическое ожидание (  ); - стандартное отклонение (СКО); - дисперсия (  ).Скос и эксцесс равны нулю:  .Интеграл вероятности имеет вид:  Стандартное нормальное распределение. Если заменить переменные (т.е. их пронормировать и заменить)  - стандартизованная случайная величина, то получим стандартное нормальное распределение с плотностью распределения в виде  а интеграл вероятности Гаусса преобразуется, и будет иметь вид  Функция табулирована [41], если таблица приведена для интеграла 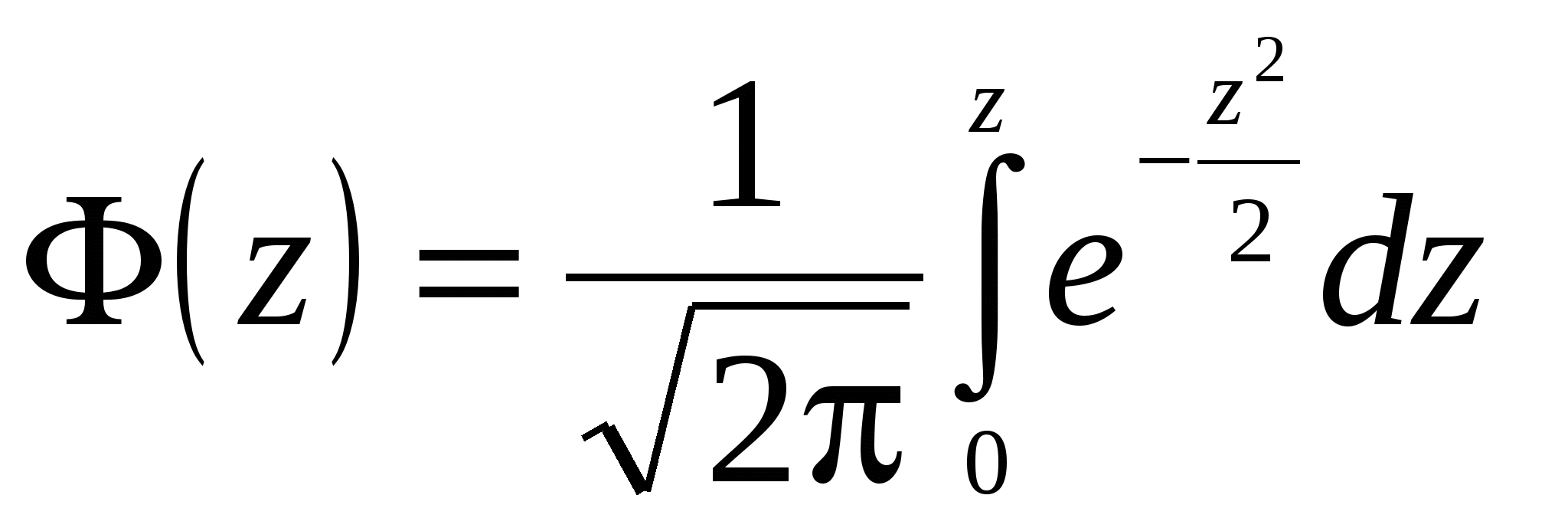 ,(её иногда называют функцией Лапласа), то в этом случае  .Примечание. При пользовании таблицами для избегания ошибок вычислений следует обращать внимание на то, для какой функции они составлены (на интеграл). Для стандартного нормального распределения  .Стандартное нормальное распределение обозначают символом N(0, 1) и называют: нормированное нормальное распределение, стандартное распределение Лапласа-Гаусса (ГОСТ Р 50779.10-2000 ). Связь с интегралом ошибок. Интегралом ошибок называют функцию  Интеграл ошибок у нас в стране распространения не получил, но за рубежом имеет применение. Интеграл вероятности Гаусса связан с интегралом ошибок следующим соотношением:  В литературе нормальный закон называют по-разному: - нормальный закон Гаусса, - Гауссовское распределение, - второй закон Лапласа, - Лаплассовское распределение, - нормированная функция Лапласа, - распределение Гаусса-Лапласа, - распределение Лапласа-Гаусса (ГОСТ Р 50779.10-2000 ). Нормальный закон распределения для погрешностей. Плотность нормального закона распределения для погрешностей имеет вид: 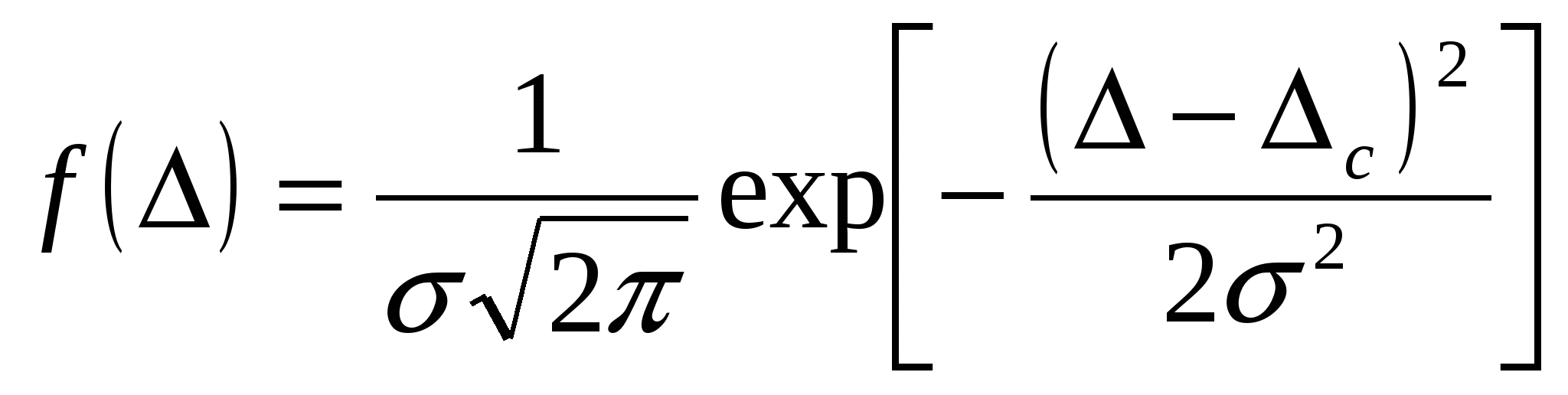  , где  .Свойства кривой распределения для случайных величин
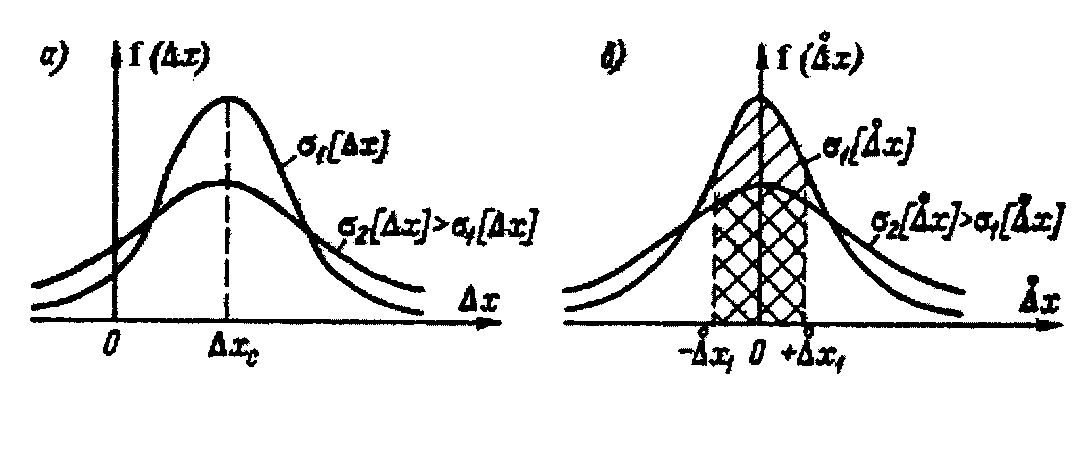 Рис. 1.2. Нормальный закон распределения погрешности измерений (а) и случайной составляющей погрешности измерений (б). В практической деятельности часто используют свойства нормального закона (рис. 1.2). Так, например, при нормальном законе распределения случайных погрешностей со среднеквадратическим отклонением  часто пользуются доверительным интервалом от —3 до +3, для которого доверительная вероятность равна 0,9973. Такая доверительная вероятность означает, что при наблюдениях в среднем из 370 случайных погрешностей только одна погрешность по абсолютному значению будет больше 3 . Так как на практике число отдельных измерений редко превышает несколько десятков, появление даже одной случайной погрешности, большей, чем 3, маловероятное событие, наличие же двух подобных погрешностей почти невозможно. Это позволяет с достаточным основанием утверждать, что все возможные случайные погрешности измерения, распределенные по нормальному закону, практически не превышают по абсолютному значению 3 (правило «трех сигм»). Отсюда же исходит и «правило шести сигм» (интервал от -3 до +3 равен 6), применяемое в Всеобщем управлении качеством (TQM). Интервалы шире чем 3 , как правило, применяют очень редко, так как это считается излишним, однако, например, в технике грузовые устройства (краны, гаки) рассчитываются с четырехкратным запасом прочности.Распределение Стьюдента, (t-распределение). Распределение вероятностей непрерывной случайной величины, с плотностью распределения вероятностей 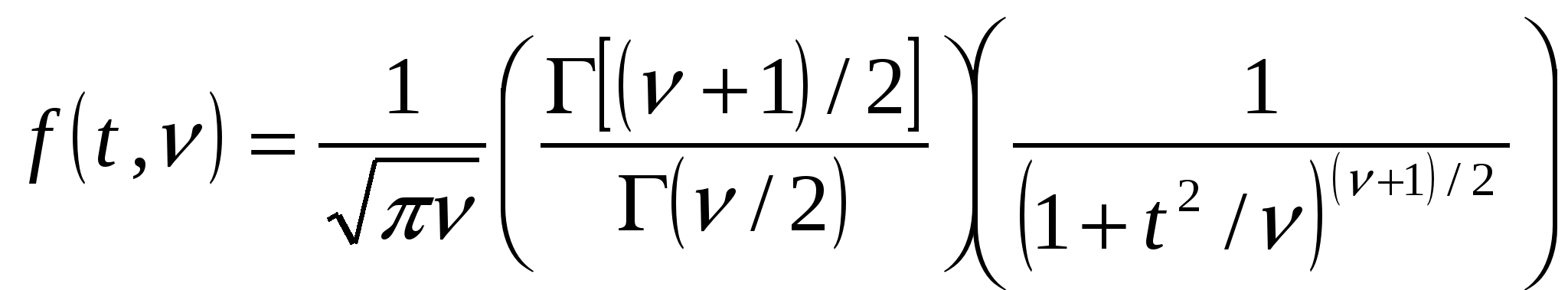 ,где  с параметром  ;Г – гамма – функция. Распределение Стьюдента с возрастанием числа степеней свободы  стремится к нормальному закону. Функция табулирована.Данный закон распределения широко используется при обработке результатов многократных измерений. Равномерный закон распределения. Если погрешность измерений с одинаковой вероятностью может принимать любые значения, не выходящие за некоторые границы, то такая погрешность описывается равномерным законом распределения. При этом плотность вероятности погрешности  постоянна внутри этих границ и равна нулю вне этих границ. Равномерный закон распределения представлен на рис. 1.3. Аналитически он может быть записан так: при  ;  при  ;  Рис. 1.3. Равномерный закон распределения  Трапециевидный закон распределения. Это распределение графически изображено на рис. 1.4, а. Погрешность имеет такой закон распределения, если она образуется из двух независимых составляющих, каждая из которых имеет равномерный закон распределения, но ширина интервала равномерных законов различна. Например, при последовательном соединении двух измерительных преобразователей, один из которых имеет погрешность, равномерно распределенную в интервале  , а другой — равномерно распределенную в интервале  , суммарная погрешность преобразования будет описываться трапециевидным законом распределения.Треугольный закон распределения (закон Симпсона). Этораспределение (см. рис. 1.4, б) является частным случаем трапециевидного, когда составляющие имеют одинаковые равномерные законы распределения. 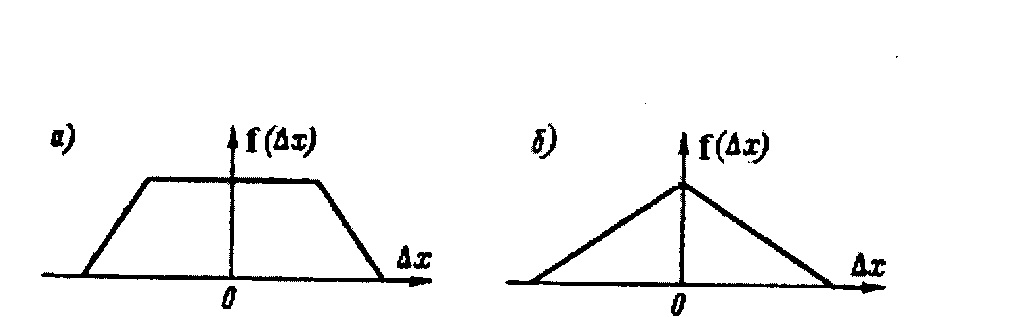 Рис. 1.4. Трапециевидный (а) и треугольный (б) законы распределения Средства измерений, их классификации Для обнаружения физических свойств объектов без участия органов чувств человека используются специальные технические устройства – индикаторы. С их помощью устанавливается наличие измеряемой физической величины и регистрируется изменение ее размера. Например, стрелка магнитного компаса является индикатором магнитного поля, лакмусовая бумажка – индикатор активности ионов водорода в растворах. Индикаторы характеризуются порогом обнаружения (порогом чувствительности). Чем меньше порог обнаружения, тем более слабое проявление свойства регистрируется индикатором. Технические средства, предназначенное для измерений называются средствами измерений. Средства измерений включают в себя меры, эталоны, измерительные преобразователи, измерительные приборы и вспомогательные средства. Созданные на их основе сложные измерительные комплексы называются измерительными установками и измерительными системами. К числу средств измерения относятся также измерительно-вычислительные системы и комплексы Мерой называется средство измерений, предназначенное для воспроизведения физической величины заданного размера (например, гиря - мера массы). Все множество мер делится на однозначные и многозначные. Меры, воспроизводящие физические величины лишь одного размера, называются однозначными, а меры, которые могут воспроизводить ряд размеров физической величины, непрерывно заполняющих некоторый промежуток между определенными границами называется многозначными (к примеру, миллиметровая линейка или вариометр). Объединяясь в различных сочетаниях для воспроизведения некоторых промежуточных или суммарных дискретных размеров величин, меры образуют наборы или магазины. В наборе меры могут выполнять свои функции как в отдельности, так и в различных сочетаниях (набор концевых мер длины, набор гирь и т.п.), а в магазинах они объединяются в одно механическое целое, снабженное специальными переключателями, которые связаны с отсчетными устройствами. К однозначным мерам относятся также стандартные образцы и образцовые вещества, которые представляют собой специально оформленные тела или пробы вещества определенного и строго регламентированного содержания, одно из свойств которых в определенных условиях является величиной с известным значением. К ним, в частности, относятся образцы для определения механических свойств металлов. Действительные значения физической величины, воспроизводимые мерой, называются действительными значениями меры. Они получаются при измерениях путем исключения систематических погрешностей и сведения к минимуму параметров случайных погрешностей. Погрешность определения действительного значения меры называется погрешностью аттестации меры. Указанные на мере значения величин, которым должны быть равны действительные значения мер с допустимыми отклонениями, называются номинальными значениями меры. Номинальное и действительное значения меры, а также погрешность ее аттестации заносятся в специальные свидетельства, которыми сопровождается мера. Разность между номинальным и действительным значениями называется погрешностью меры, которая всегда постоянна. Величина, обратная погрешности по знаку, называется поправкой к номинальному значению меры. Меры подразделяются на разряды (меры 1, 2, 3, 4-го разрядов) и классы в зависимости от погрешности аттестации. Меры, которые предназначены для поверки средств измерения, называются образцовыми, а меры, поделенные на классы и используемые при технических измерениях, называются рабочими. Измерительным преобразователем называется средство измерений, служащее для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и (или) хранения, но не подлежащей непосредственному восприятию наблюдателем. Измерительные преобразователи обычно входят в качестве составных элементов сложных измерительных комплексов и систем. Величина, которая подлежит преобразованию измерительным преобразователем, называется входной, а результат преобразования – выходной величиной. Соотношение между входной и выходной величинами называется функцией преобразования. Если в результате преобразования физическая природа входной величины не изменяется, а функция преобразования является линейной, то такой измерительный преобразователь называется масштабным (или усилителем), например, измерительный микроскоп. Если же физическая природа выходной величины отличается от входной, то такой измерительный преобразователь получает название по видам этих величин (например, электромеханический вибровозбудитель колебаний). В зависимости от места, занимаемого в приборе, преобразователи делятся на первичные, передающие и промежуточные. В первичном преобразователе измеряемая физическая величина подводится к нему непосредственно; в передающем преобразователе на выходе образуются величины, удобные для их регистрации и передачи на расстояние; промежуточный преобразователь в измерительной цепи занимает место после первичных. Измерительные приборы – это средства измерений, предназначенные для получения измерительной информации о величине, подлежащей измерению, в форме, удобной для восприятия наблюдателем. Совокупность измерительных приборов, измерительных эталонов, стандартных образцов, вспомогательных средств измерений и инструкций, необходимых для проведения измерений, называется измерительным оборудованием. По принципу действия приборы подразделяются па приборы прямого действия и приборы сравнения. В приборах прямого действия измеряемая величина подвергается ряду последовательных преобразований в одном направлении. Они состоят из ряда блоков, предназначенных для преобразования измеряемой величины в более мощный сигнал, который может приводить в действие подвижные органы отсчетных устройств, проградуированных с помощью соответствующих мер. Такие приборы являются наиболее распространенными. К их числу относятся, например, амперметры, вольтметры, манометры и т.п. Приборы сравнения основаны на использовании приема сравнения измеряемых величин с величинами, значения которых известны, Сравнение активных величин (несущих в себе некоторый запас энергии: сил, давлений, электрических напряжений и т.п.) производится с помощью компенсационных цепей, а сравнение пассивных величин (электрическое, гидравлическое и т.п. сопротивления) – с помощью мостовых цепей. Весьма часто пассивные величины предварительно преобразовываются в активные или наоборот. Приборы сравнения обладают более высокой точностью, чем приборы прямого действия. По способу отсчета значений измеряемых величин приборы подразделяются на показывающие (в том числе на аналоговые и цифровые) и на регистрирующие. Среди показывающих приборов наибольшее распространение имеют аналоговые, отсчетные устройства которых состоят из двух элементов: шкалы, обычно соединенной с корпусом, и указателя, связанного с подвижной системой прибора. В цифровых приборах отсчет осуществляется с помощью механических, электронных или других отсчетных устройств, а выходная информация представляется в цифровом виде. По способу записи измеряемой информации регистрирующие приборы делятся на самопишущие и печатающие. В самопишущих приборах запись показаний представляется в виде непрерывных графиков или диаграмм (например, барограф или шлейфовый осциллограф). В печатающих приборах выходная информация выдается в числовой форме на бумажных носителях. К группе вспомогательных средств измерений относятся такие средства, которые влияют на метрологические свойства других средств измерений при их непосредственном применении по назначению или поверке. По показаниям вспомогательных средств измерений вычисляют поправки к результатам измерений основных величин. К вспомогательным средствам измерений могут быть отнесены, например, термометры, психрометры и т.п. Когда для измерения какой-либо величины недостаточно одного измерительного прибора, создают комплексы расположенных в одном месте средств измерений, называемых измерительными установками, от которых сигнал измерительной информации представляется как и для измерительного прибора в форме, удобной для наблюдателя. Измерительные системы – это также комплексы средств измерений, расположенных в одном месте, предназначенных для выработки сигнала измерительной информации в форме, удобной не только для одного наблюдателя, но и для автоматической обработки результатов измерений, передачи их на расстояние или использования в автоматических системах управления. Измерительно-вычислительные комплексы (ИВК) – функционально объединенная совокупность средств измерений, ЭВМ и вспомогательных устройств, предназначенных для выполнения в составе измерительной системы конкретной измерительной задачи Отличием средства измерений от других технических устройств является то, что оно предназначено для получения измерительной информации) и имеет нормированные метрологические характеристики. По метрологическому назначению средства измерений делятся на: 1) рабочее средство измерений - средство измерений, предназначенное для измерений не связанных с передачей размера единицы другим средствам измерения (бывают лабораторные, производственные и полевые); 2) эталон единицы величины - средство измерений, предназначенное для воспроизведения и хранения единицы величины (или кратных либо дольных значений единицы величины) с целью передачи ее размера другим средствам измерений данной величины; 3) первичный эталон – эталон, обеспечивающий воспроизведение единицы с наивысшей в стране точностью; 4) исходный эталон – эталон, обладающий наивысшими метрологическими свойствами (в данной лаборатории, организации, на предприятии), от которого передают размер единицы подчиненным эталонам и имеющимся средствам измерения; 5) государственный первичный эталон – первичный эталон, признанный решением уполномоченного на то государственного органа в качестве исходного на территории Российской Федерации. Рабочие эталоны 1-го, 2-го, 3-го и 4-го разряда предназначены для передачи единицы величины рабочим СИ. Государственные эталоны единиц величин используются в качестве исходных для воспроизведения и хранения единиц величин с целью передачи их размеров всем средствам измерений данных величин на территории Российской Федерации. Метрологические характеристики средств измерений - характеристики свойств средств измерений, оказывающие влияние на результаты и погрешности измерений. Эти характеристики называют еще точностными характеристиками средств измерении. Информация о назначении и метрологических характеристиках приведена в документации на средства измерений (в государственном стандарте, в ТУ, в паспорте на средство измерения). Характерной особенностью измерительной техники является широкое распространение измерительных процессов, в которых одновременно участвуют несколько средств измерений, измеряющих разные физические величины и основанных на разных принципах действия. Это вызывает необходимость нормировать метрологические характеристики различных средств измерений на единой, принципиальной основе. По метрологическим характеристикам средств измерений решается ряд задач, важных для обеспечения единства измерений: -определение погрешности результата измерений (одной из составляющих погрешности измерений является погрешность средств измерений), -выбор средств измерений по точности по известным условиям их применения и требуемой точности измерений (эта задача является обратной по отношению к задаче определения погрешности измерений); -сравнение средств измерений различных типов с учетом условий их применения; -замена одного средства измерений на другое - аналогичное; оценка погрешности сложных измерительных систем и др. Нормированные метрологические характеристики выражают в форме, удобной для обоснованного решения перечисленных выше задач и одновременно достаточно простого осуществления их контроля при поверке или калибровке. В практике применения средств измерений широко используется выражение - класс точности. Это характеристика зависит от способа выражения пределов допускаемых погрешностей средств измерений. Впервые "класс точности" был введен в тридцатые годы применительно к стрелочным приборам и определял основную погрешность средств измерений (погрешность средств измерений в нормальных условиях). Введение класса точности преследовало цель классификации средств измерений по точности. В настоящее время, когда схемы и конструкции средств измерений усложнились, а области применения средств измерений весьма расширились, на погрешность измерений стали существенно влиять и другие факторы. В частности, изменения внешних условий (температура окружающей среды, механические нагрузки на средства измерений и т.д.), а также характер изменения измеряемых величин во времени. Основная погрешность измерительных приборов перестала быть действительно основной составляющей погрешности измерений и класс точности не позволяет в полной мере решать практические задачи, перечисленные выше. Область практического применения характеристики "класс точности" ограничена только такими средствами измерений, которые предназначены для измерения статических величин. В международной практике "класс точности" устанавливается только для небольшой части приборов. Требования к назначению, применению и обозначению "классов точности" регламентированы в ГОСТ 8.401-80 " Государственная система обеспечения единства измерений. Классы точности средств измерений. Общие требования ". Метрологическое обеспечение средств измерений зависит от сферы их использования. Сферы распространения государственного метрологического контроля и надзора приведены в федеральном Законе "Об обеспечении единства измерений". В сферах распространения государственного метрологического контроля и надзора используемые типы средств измерений должны быть утверждены и включены в Государственный реестр средств измерений, который ведет Всероссийский научно-исследовательский институт метрологической службы (ВНИИМС). На средство измерений утвержденного типа и на эксплуатационные документы наносится знак утверждения типа установленной формы и выдается сертификат. Средства измерений при эксплуатации должны подвергаться периодической поверке органами Государственной метрологической службы или аккредитованными метрологическими службами юридических лиц. На поверенное средство измерений наносится клеймо и выдается свидетельство установленной формы. Перечни средств измерений, подлежащих поверке, составляются метрологическими службами юридических лиц и направляются в органы Государственной метрологической службы. При осуществлении Государственного метрологического надзора контролируется правильность и полнота этих перечней, а также состояние и применение средств измерений. Средства измерений, применяемые вне сферы распространения государственного метрологического контроля и надзора, калибруются метрологической службой предприятия по эталонам, соподчиненным государственным эталонам единиц величин. Метрологические службы юридических лиц могут быть аккредитованы на право проведения калибровочных работ органами Государственной метрологической службы в Российской системе калибровки (РСК). Порядок аккредитации на право выполнения калибровочных работ устанавливается Госстандартом России. Требования к средствам измерений определены ст. 9 федерального закона "Об обеспечении единства измерений", которым предусмотрены следующие положения:
Для передачи размеров единиц от государственного эталона рабочим средствам измерений создана система эталонов, которые по точности подразделяются на разряды. Передача размеров единиц осуществляется путем поверки или калибровки средств измерений. Поверка средств измерений - совокупность операций, выполняемых органами Государственной метрологической службы (другими уполномоченными на то органами, организациями) с целью определения и подтверждения соответствия средства измерений установленным техническим требованиям. Поверка средства измерений заключается в определении погрешностей средства измерений и в установлении его пригодности к применению. Проведение поверки позволяет установить, находятся ли метрологические характеристики средств измерений в заданных пределах. Процедура поверки средств измерений регламентируется различными документами (государственными стандартами, инструкциями, методическими указаниями и др.), соблюдение требований которых обязательно. Калибровка средств измерений - совокупность операций, выполняемых с целью определения и подтверждения действительных значений характеристик и (или) пригодности к применению средств измерений, не подлежащих государственному метрологическому контролю и надзору. Соподчинение Государственного эталона, вторичных, а также системы разрядных эталонов и рабочих средств измерений установлено государственной поверченной схемой. Поверочная схема – утвержденный в установленном порядке документ, устанавливающий средства, методы и точность передачи размеров единиц от государственного эталона рабочим средствам измерений. Поверочные схемы разделяют на государственные и локальные, Государственные поверочные схемы регламентируются государственными стандартами и распространяются на все средства измерений данного вида. Локальные поверочные схемы предназначены для метрологических служб Государственных органов управления и юридических лиц. Все локальные схемы должны соответствовать требованиям соподчиненности, которая определена государственной поверочной схемой. Поверочные схемы состоят из чертежа и текстовой части. На чертеже указывают: наименование средств измерений, диапазоны значений физических величин, обозначения и значения погрешностей, наименования методов поверки. Текстовая часть состоит из вводной части и пояснений к элементам поверочной схемы. Метрологические показатели средств измерений При выборе средства измерения в зависимости от заданной точности изготовления деталей необходимо учитывать их метрологические показатели. К ним относятся: 1. Длина деления шкалы - это расстояние между серединами двух соседних отметок (штрихов, точек и т.п.) шкалы. 2. Цена деления шкалы - это разность значений величин, соответствующих двум соседним отметкам шкалы (у микрометра она равна 0,01мм) . 3. Градуировочная характеристика - зависимость между значениями величин на выходе и входе средства измерений. Градуировочную характеристику снимают для уточнения результатов измерения. К ним относятся, например, номинальная статическая характеристика преобразования измерительного преобразователя, номинальное значение однозначной меры, пределы и цена деления шкалы, виды и параметры цифрового кода средств измерений, предназначенных для выдачи результатов в цифровом коде. 4. Диапазон показаний - область значений шкалы, ограниченная конечным и начальным значениями шкалы, т. е. наибольшим и наименьшим значениями измеряемой величины. Например, для оптиметра ИКВ-3 диапазон показаний составляет 0,1мм. 5. Диапазон измерений - область значений измеряемой величины с нормированными допускаемыми погрешностями средства измерения. Для того же оптиметра он составляет 0-200мм. 6. Чувствительность прибора - отношение изменения сигнала на выходе измерительного прибора к изменению измеряемой величины (сигнала на входе). Так, если при измерении диаметра вала d=100мм. Изменение измеряемой величины d=0,01мм вызвало перемещение стрелки показывающего устройства на l=10мм, абсолютная чувствительность прибора составляет S=l/d=10/0,01=1000. Для шкальных измерительных приборов абсолютная чувствительность численно равна передаточному отношению. 7. Вариация (нестабильность) показаний прибора – алгебраическая разность между наибольшим и наименьшим результатами измерений при многократном измерении одной и той же величины в неизменных условиях. 8. Стабильность средства измерений - свойство, выражающее неизменность во времени его метрологических характеристик (показаний). Метрологические характеристики средств измерений Все средства измерений, независимо от их исполнения, имеют ряд общих свойств, необходимых для выполнения ими функционального назначения. Технические характеристики, описывающие эти свойства и оказывающие влияние на результаты и погрешности измерений, называются метрологическими характеристиками средств измерений. В зависимости от специфики и назначения средств измерений нормируются различные наборы или комплексы метрологических характеристик. Однако эти комплексы должны быть достаточны для учета свойств средств измерений при оценке погрешностей измерений. Метрологические характеристики, входящие в установленный комплекс, выбирают такими, чтобы обеспечить возможность их контроля при приемлемых затратах. В эксплуатационной документации на средства измерений указывают рекомендуемые методы расчета инструментальной составляющей погрешности измерений при использовании средств измерения данного типа в реальных условиях применения. По ГОСТ 8.009 – 84 “ГСИ. Нормируемые метрологические характеристики средств измерений” предусмотрена следующая номенклатура метрологических характеристик: 1). Характеристики, предназначенные для определения результатов измерений (без введения поправок): функция преобразования измерительного преобразователя – f(x); значение однозначной или многозначной меры – у; цена деления шкалы измерительного прибора или многозначной меры; вид входного кода, число разрядов кода, цена единицы наименьшего разряда средств измерений, предназначенных для выдачи результатов в цифровом коде. 2). Характеристики погрешностей средств измерений включают: значение погрешности, ее систематические и случайные составляющие, погрешности случайной составляющей слН от гистерезиса – вариация Н выходного сигнала (показания). Для систематической составляющей сист погрешности средств измерений выбирают характеристики из числа следующих: значение систематической систематической составляющей сист; значение систематической составляющей сист, математическое ожидание М[сист] и среднее квадратическое отклонение [сист] систематической составляющей погрешности. Для случайной составляющей сл погрешности выбирают характеристики из числа следующих: среднее квадратическое отклонение [сл] случайной составляющей погрешности; среднее квадратическое отклонение [сл] случайной составляющей погрешности и нормализованная автокорреляционная функция rсл() или функция спектральной плотности Sсл() случайной составляющей погрешности. В нормативно-технической документации на средства измерений конкретных видов или типов допускается нормировать функции или плотности распределения вероятностей систематической и случайной составляющих погрешности. 3. Характеристики чувствительности средств измерений к влияющим величинам выбираются из числа следующих: функция влияния (); изменения () значений метрологических характеристик средства измерения, вызванные изменением влияющих величин в установленных пределах. 4. Динамические характеристики отражают инерционные свойства средства измерений при воздействии на него меняющихся во времени величин - параметров входного сигнала, внешних влияющих величин, нагрузки. По степени полноты описания инерционных свойств средств измерений динамические характеристики делятся на полные и частные. К полным динамическим характеристикам относятся: дифференциальное уравнение, описывающее работу средства измерений; передаточная функция; переходная характеристика; импульсная переходная характеристика; амплитудно-фазовая характеристика; амплитудно-частотная характеристика для минимально-фазовых средств измерения; совокупность амплитудно-фазовых и фазово-частотных характеристик. Частичными динамическими характеристиками могут быть отдельные параметры полных динамических характеристик или характеристики, не отражающие полностью динамических свойств средств измерений, но необходимые для выполнения измерений с требуемой точностью (например, время реакции, коэффициент демпфирования, значение амплитудно-частотной характеристики на резонансной частоте, значение резонансной собственной круговой частоты). Комплекс их оговаривается в соответствующих стандартах. Нормы на отдельные метрологические характеристики приводятся в эксплуатационной документации (паспорте, техническом описании, инструкции по эксплуатации и т. д.) в виде номинальных значений, коэффициентов функций, заданных формулами, таблицами или графиками пределов допускаемых отклонений от номинальных значений функций. В ГОСТ 8.009 – 84 приведены способы нормирования рассмотренных выше метрологических характеристик. 5. Характеристики СИ, способные влиять на инструментальную погрешность прибора 6. Неинформативные параметры выходного сигнала СИ. Классы точности средств измерений Учёт всех нормируемых метрологических характеристик средств измерений является сложной и трудоёмкой процедурой. На практике такая точность не нужна. Поэтому для средств измерений, используемых в повседневной практике, принято деление на классы точности, которые дают их обобщённую метрологическую характеристику. Общие положения деления средств измерений на классы точности, способы нормирования метрологических характеристик и обозначения классов точности устанавливает ГОСТ 8.401-80. Класс точности средства измерений – обобщенная характеристика, определяемая пределами допускаемых и дополнительных погрешностей, а также другими свойствами, влияющими на точность, значения которых устанавливаются в стандартах. Класс точности характеризует точность приборов, но не является показателем точности. Пределы допускаемых погрешностей выражают в форме приведенной, относительной или абсолютной погрешностей. Классы точности присваиваются средствам измерений с учётом результатов государственных приёмочных испытаний. Обозначения классов точности наносятся на циферблаты, щитки и корпуса средств измерений, приводятся в нормативно-технических документах. Классы точности могут обозначаться буквами (например, М, С и т. д.) или римскими цифрами (I,II,III и т. д.). Обозначение классов точности по ГОСТ 8.401–80 может сопровождаться дополнительными условными знаками: - 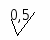 0,5, 1,6, 2,5 и т. д.- для приборов, приведенная погрешность =/ХN которых составляет 0,5, 1,6, 2,5% от нормирующего значения ХN ( - пределы допустимой абсолютной погрешности). При этом ХN принимается равным большему из модулей пределов измерений, если нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений;- - то же, что и в предыдущем случае, но при ХN равным длине шкалы или ее части;-  и т. д. - для приборов, у которых относительная погрешность =/х составляет 0,1, 0,4, 1,0% непосредственно от полученного значения измеряемой величины х; - 0,02/0,01 - для приборов, у которых измеряемая величина не может отличаться от значения х, показанного указателем, больше, чем на C + d (Хк х - 1)]%, где С и d - числитель и знаменатель соответственно в обозначении класса точности; Хк – больший (по модулю) из пределов измерений прибора. Метрологическая надежность средств измерений Метрологическая надёжность - это свойство средств измерений сохранять установленные значения метрологических характеристик в течение определённого времени при нормальных режимах и рабочих условиях эксплуатации. Она характеризуется интенсивностью отказов, вероятностью безотказной работы и наработкой на отказ. Интенсивность отказов определяется выражением  ,где L - число отказов; N - число однотипных элементов; t - промежуток времени. Для средства измерения, состоящего из n типов элементов, интенсивность отказов  ,где mi - количество элементов i-го типа. Вероятность безотказной работы 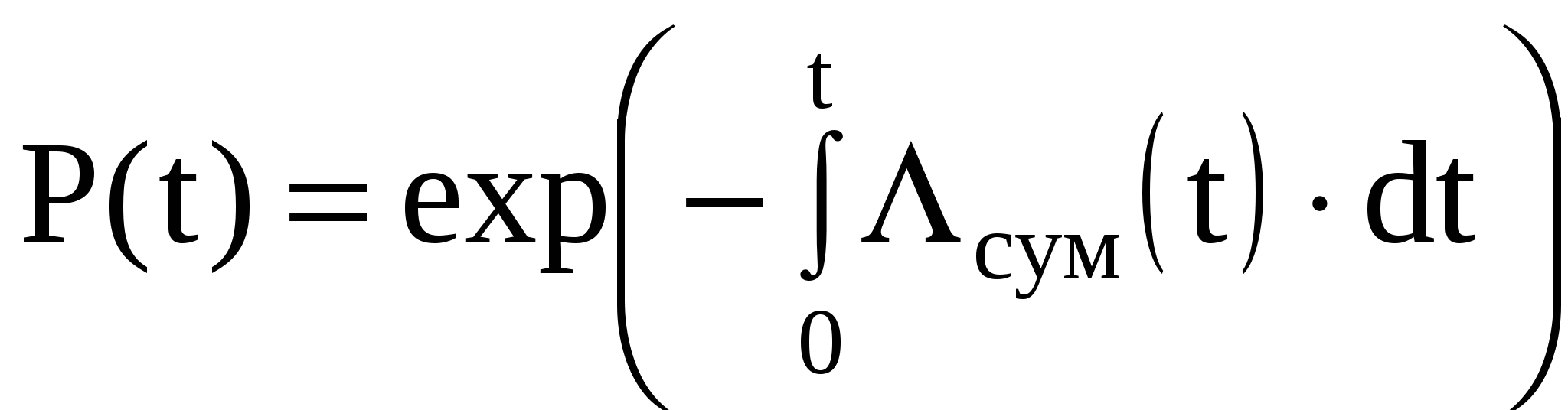 .Наработка на отказ  .Для внезапного отказа, интенсивность отказов которого не зависит от времени работы средства измерения, сум(t) = сум = const; P(t) = exp(-сумt); Tср = L/сум . Межповерочный интервал, в течение которого обеспечивается заданная вероятность безотказной работы, определяется по формуле  ,где Рмо - вероятность метрологического отказа за время между поверками; Р(t) - вероятность безотказной работы. |
.
, составляет 
.
, составляет 
.
, составляет 
.
, составляет 
.
, составляет 
.
в среднем может встретиться 1 раз на каждые 3 измерения.
в среднем может встретиться 1 раз на каждые 22 измерения.
в среднем может встретиться 1 раз на каждые 370 измерений.
в среднем может встретиться 1 раз на каждые 157870 измерений.
в среднем может встретиться 1 раз на каждые 1743983 измерений.