4КУрс_ОпКонсМод. Конспект лекций по дисциплине "моделирование обогатительных процессов" для специальности 090302 "Обогащение полезных ископаемых"
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
Рис.3.6. Схема расположения векторов полных фракционных классов. Вычисление частного вектора yas(i, j) выполняем по формуле [23] yas(i, j) = [YAS(i, j) + YAS(i-1, j-1)] – [YAS(i-1, j) + YAS(i, j-1)]. (3.2) где yas(i, j) - частный вектор - частный фракционный класс с верхней крупностью номер i и верхней зольностью номер j и нижней крупностью номер i-1 и нижней зольностью номер j-1; YAS(i, j) - полный вектор - фракционный класс с верхней крупностью номер i и верхней зольностью номер j. Контрольные вопросы. 1. В чём сущность метода совместного описания ситового и фракционного составов? 2. В чём состоит идея форматирования массивов данных сепарабельности? Литература к лекции: [8], [13], [14] Для заметок к лекции № 3.3 Лекция 3.4 Преобразование фракционных характеристик Рассматриваемые вопросы: Сущность прямого линейного преобразования фракционных характеристик. Область применения обратного линейного преобразования. Алгоритмы и программы линейного и нелинейного преобразования фракционных характеристик. Основное свойство обогатительных процессов состоит в изменении сепарабельности сепарируемого материала за счёт раскрытия минералов, но только в одной работе [15] есть ссылка на предложение П. К. Сена и С. Пойя определять степень раскрытия минералов по результатам флотации. Очевидно, нужен метод описания такого изменения распределения фракций. Линейное преобразование. Постановка задачи. Постулируем, что есть такой процесс, измельчение в котором протекает пропорционально содержанию горючей массы (при хрупкости угольных частиц) или, то же самое, пропорционально зольности (за счет дробления или размокания породы). Пусть имеются n фракций с выходами 1,i и зольностью 1,i, где i = 1, 2, , n. Требуется линейно преобразовать эти данные так, чтобы суммарный выход стал равным величине u, а суммарная зольность стала равной z. Метод решения задачи. Применим уравнение прямой линии где A0 и A1 - неизвестные коэффициенты уравнения этой прямой, 1,i - аргумент этой прямой в i-ой точке, i = 1, 2, , n, к преобразованию выходов фракций После суммирования откорректированных выходов фракций по всем индексам i = 1, 2, , n должен сохраниться ,баланс по выходу где u - суммарный выход, и по суммарной зольности где z - суммарная зольность. Объединяя уравнения (3.5) и (3.6) в систему и решая эту линейную систему уравнений относительно неизвестных коэффициентов A0 и A1 для заданных значений u и z методом исключения, получим искомые коэффициенты в следующей, удобной для вычислений, форме: 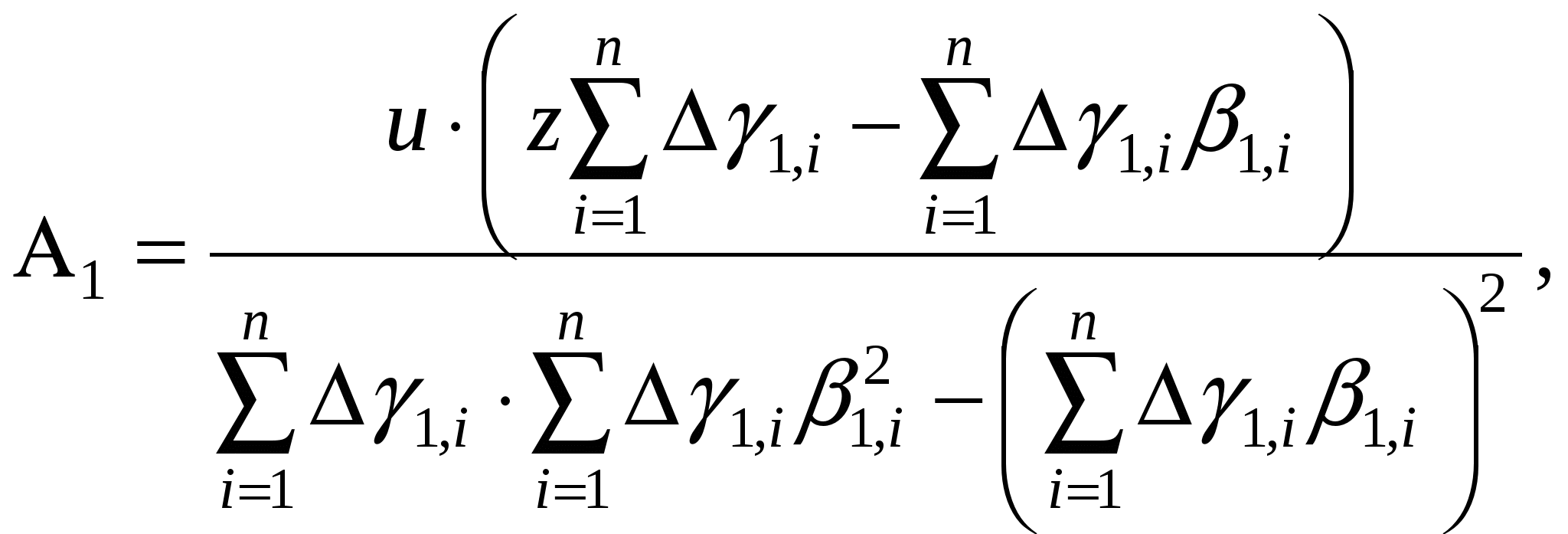 (3.7) (3.7)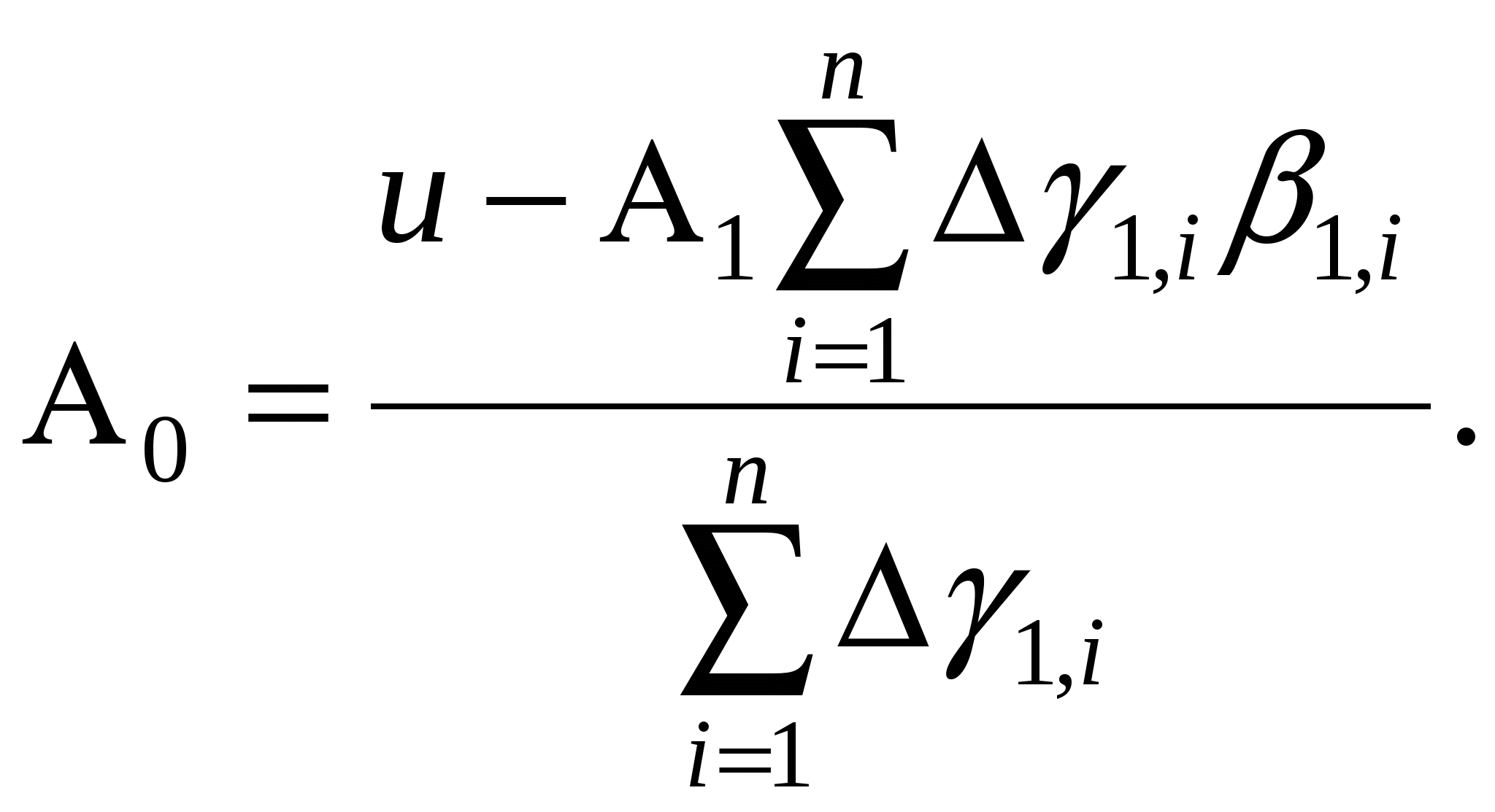 (3.8) (3.8)Теперь, с учётом коэффициентов A1 и A0, искомые значения откорректированных выходов фракций 2,i определятся из (3.4). Линейное преобразование сепарационных характеристик полезно также и для обратной задачи по отношению к рассмотренной - для моделирования самоизмельчения, образования шлама и др. Постановка и решение названой обратной задачи ещё проще. Исходными условиями для линейного преобразования являются коэффициенты измельчения чистого угля iu, % и чистой породы ip, %. На основании этих параметров вычисляются коэффициенты уже рассмотренной линейной модели (3.3) по нижеследующим формулам: Теперь, с учётом коэффициентов A0 и A1 по (3.19) и (3.10), искомые значения выходов фракций 2,i определятся из формулы (3.4). Эти алгоритмы действительно всегда обеспечивают эффективную корректировку баланса, создание фракционного состава по аналогу, точное описание процессов самоизмельчения [16]. Нелинейное преобразование. Метод решения задачи. Замена преобразующего уравнения прямой линии (3.6) уравнением параболы позволяет локализовать эффект уменьшения содержания фракций именно в зоне минимума этой параболы. Фиксация положения минимума преобразующей функции в зоне зольности наиболее легко разрушающихся (раскрывающихся) фракций промежуточного продукта одновременно упрощает алгоритм до уровня уже рассмотренного линейного преобразования. Затем назначается величина прогиба параболы через её связь с параметрами и характеристиками процессов дробления или измельчения [16]. Контрольные вопросы.
Литература к лекции: [15], [16] Для заметок к лекции № 3.4 Лекция 4.1 Определение области сепарабельности угля Рассматриваемые вопросы: Аппроксимационное описание распределения фракций в продукты сепарации с помощью характеристики извлечения фракций. Метод Тромпа и его недостаток. Определение границ расположения переменной области сепарабельности сепарационного процесса. Факторы формирования области сепарабельности. Графическое описание области сепарабельности. Описание сепарационного процесса следует выполнять в соответствии с закономерностью области его (процесса) существования, которая названа областью сепарабельности [17, 18]. Знание этой области необходимо для прогноза возможного распределения фракций исходного угля по продуктам сепарации. Прогноз результатов сепарации редукцией критерия селективности, или как это названо в [19] – приведение результатов обогащения к базовому варианту методом редукции критерия сепарабельности заключается в следующем. Если в функцию (2.21) подставить условие корректности теоретического эксперимента по отношению к реальному процессу (выход т= к) [1] то после возведения указанной функции во вторую степень и сжатия описания этой функции вводом формальных обозначений где θ – показатель селективности, вычисленный по (2.21) для данных оцениваемого процесса, прогнозируемую зольность концентрата получим решением квадратного уравнения [20] как 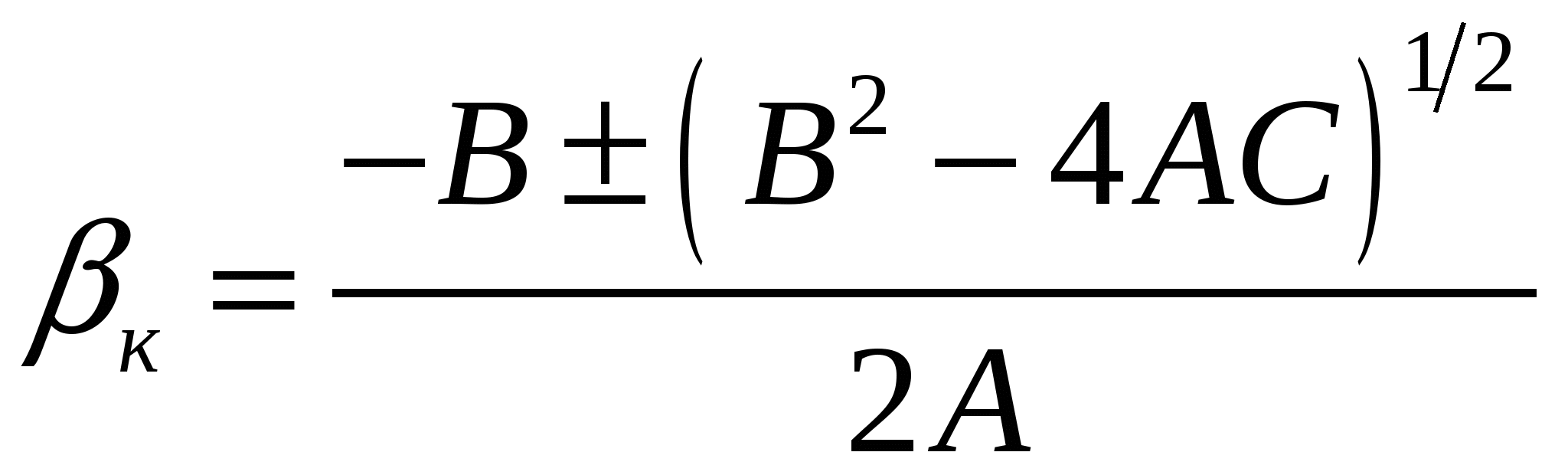 . (4.5) . (4.5)Например, пусть в предыдущем (старом) эксперименте оценка сепарабельности по (2.21) составила 0,90 (все параметры выражаем в долях). Результаты нового эксперимента при зольности исходного угля βи=0,382, заданной зольности разделения λр=0,313, выходе концентрата γк=),548, его зольности βк=0,163 и зольности теоретического (найденного по кривым обогатимости) концентрата βт=0,15 тоже можно оценить по (2.21), но такая оценка для экономиста будет не предметной. По формулам (4.1)-(4.5), получим: Принимаем значение зольности βк=0,376-0,205=0,171. Таким образом, снижение зольности концентрата составило 0,171-0,163=0,008. “Красивое” по своей структуре (4.5) решение справедливо только вблизи точки описываемого реального процесса и поэтому область его применения ограничена сравнительной оценкой результатов обогащения по традиционной методике определения экономической эффективности внедрения нового мероприятия по усовершенствованию технологии обогащения. Для решения задачи прогноза распределения фракций в продукты сепарации необходимо определить закономерность формирования области сепарабельности угля по всему диапазону распределения его фракций. Наиболее строго прогноз распределения фракций исходного угля в продукты сепарации базируется на современной идее визуального моделирования области сепарабельности. Принимается следующий постулат [10, 19, 21, 22]: распределение фракций продукта наихудшей сепарации является отображением распределения фракций исходного материала в пределах выхода полученного продукта. На основе этого постулата определена область сепарабельности угля и разработан метод прогноза распределения фракций угля по продуктам сепарации. Схема области дана рис.4.1. 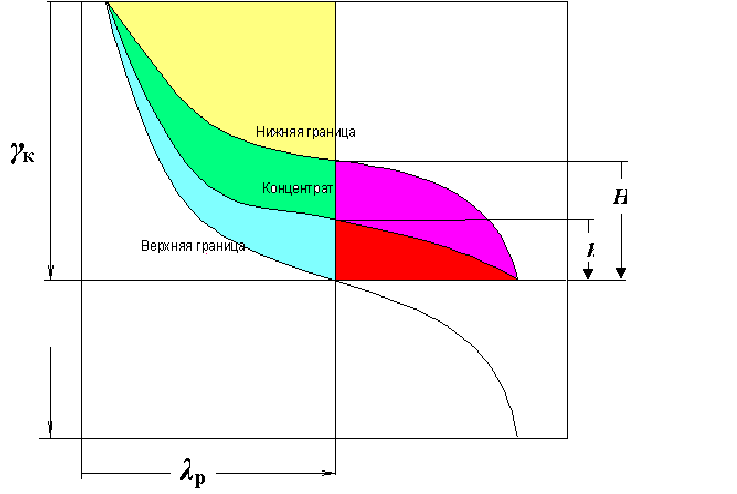 Рис.4.1. Схема выделения области сепарабельности на кривых Анри Экспериментальные исследования [10, 19] показывают, что реально всегда имеет место только локальное засорение фракций, сосредоточенное около разделительной точки процесса сепарации в форме треугольника ошибок/засорения. Этот треугольник учитывает относительность диапазонов потерь и засорения к заданной зольности разделения тогда и только тогда, когда он отсекается от выровненной области сепарабельности горизонтальной прямой. Контрольные вопросы.
Литература к лекции: [1, 10, 17, 18, 19, 21, 22] Для заметок к лекции № 4.1 Лекция 4.2 Закономерность распределения фракций сепарации Рассматриваемые вопросы: Адаптація метода Тромпа к описанию сепарации. Формула определения степени преобразования нормального закона распределения для аппроксимации кривой Тромпа. Приближенность этого метода. К закономерности распределения фракций из области сепарабельности исходного угля по продуктам сепарации можно применить альтернативный вариант описания по методу Тромпа, представляющего распределение извлечения фракций в концентрат как сепарационную характеристику процесса сепарации с предположением, что извлечение разделительной фракции в продукт сепарации составляет величину 0,5 (50%), хотя ещё в работе [23] подчёркивалось, что это не точное утверждение. Действительно, пусть даны характеристики распределения исходного материала и и продукта прод.. Если засорение продукта локальное, то можно доказать, что извлечение разделительной фракции Так как при локальном засорении основание треугольника погрешности располагается параллельно кривой кн и производная от прод. равна производной от функции по (4.6), а извлечение фракций по определению выражается отношением производных (плотностей распределения зольностей) 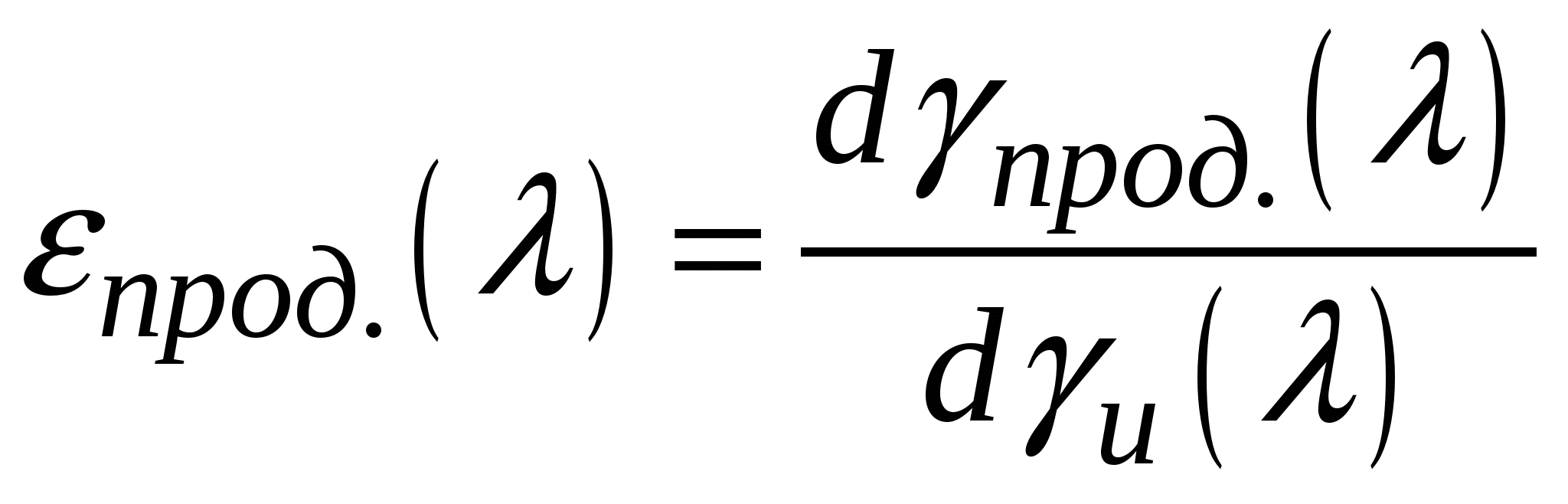 , (4.7) , (4.7)то, раскрывая здесь числитель для =р, получаем (4.6). Так, если выход концентрата составит 60% или 0,6, то извлечение разделительной фракции тоже будет равно 0,6. Обычно кривую Тромпа аппроксимируют симметричной функцией нормального распределения случайных величин. Указанное различие между этими зависимостями можно устранить, например, возведением величины извлечения разделяемой фракции Eр в степень V такую, что будет обеспечено её равенство с вероятностью функции нормального распределения при г(0) = 0,5: pV = г(0) при г(0) = 0,5 . (4.9) Для доказанной закономерности (!) (4.6) и указанного значения г(0) = 0,5 из (4.9) после логарифмирования получим показатель степени Формулы (4.9) и (4.10) дают возможность вычислить характерные величины извлечения (г(0)) для любых других значений г(0). Пример применения этого алгоритма иллюстрируется рис.4.2. 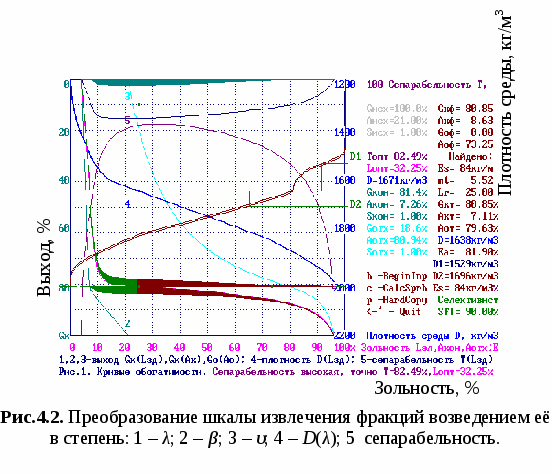 По кривой извлечения фракций при выходе концентрата к = 80,85% для характеристического извлечения (г(0)=0,25) = 0,6537 программой найдена характеристическая плотность на высокозольной ветви кривой D2=1696 кг/м3 и для характеристического извлечения (г(0)=0,75) = 0,9156 на низкозольной ветви кривой извлечения фракций определена характеристическая плотность D1 = 1529кг/м3. При этом ошибка сепарации составила величину ES84 кг/м3 на плотности разделения Dр = 1638 кг/м3. Следует отметить, что модифицированный метод Тромпа обеспечивает прогноз фракционного состава продуктов сепарации с обоснованной величиной извлечения разделительной фракции, но ошибки сепарации при этом распределяются по всему диапазону исходных фракций и источник этих ошибок не очевиден – это или распределение фракций исходного угля или дисперсия фактора разделения. Поэтому мера Epm оказывается необоснованной. Следовательно, метод прогноза распределения фракций по области сепарабельности является более обоснованным и вместе с тем более простым и удобным для практических применений. Контрольные вопросы.
Литература к лекции: [23] Для заметок к лекции № 4.2 Лекция 4.3 Нормирование показателя селективности сепарации Рассматриваемые вопросы: Величина извлечения разделительной фракции в продукт сепарации. Зависимость распределения фракций в кондиционный и некондиционный продукты от характеристик и параметров процесса сепарации. Недостаточность только экономического подхода , без учёта технологических представлений, для оценки селективности и особенно избирательности процесса сепарации. Результаты многочисленных вычислений для различных исходных данных показывают, что величина показателя селективности по (2.13) обычно не опускается ниже 0,5 или 50%. Очевидно, экономический подход к оценке эффективности обогатительных процессов неверно устанавливает нижнюю границу возможности обогащения. Чтобы исключить субъективность в выборе нормы нижнего уровня показателя (2.13), следует выполнить условия корректности сопоставления промышленного и лабораторного экспериментов по И. М. Верховскому (4.1), то же и для отходов фактических х и лабораторных хл, Также следует обратить внимание на часть положительного экономического эффекта, которая включена в оценки всех продуктов показателя (2.21), но не является следствием проявления эффекта разделения, так как входит и в оценку эффекта наихудшего процесса (см. рис.4.1, жёлтая область). Поэтому в структуру критерия (2.13) вносятся изменения вычетанием из числителя и знаменателя раздельно для блоков оценки концентрата и хвостов наихудших эффектов по концентрату 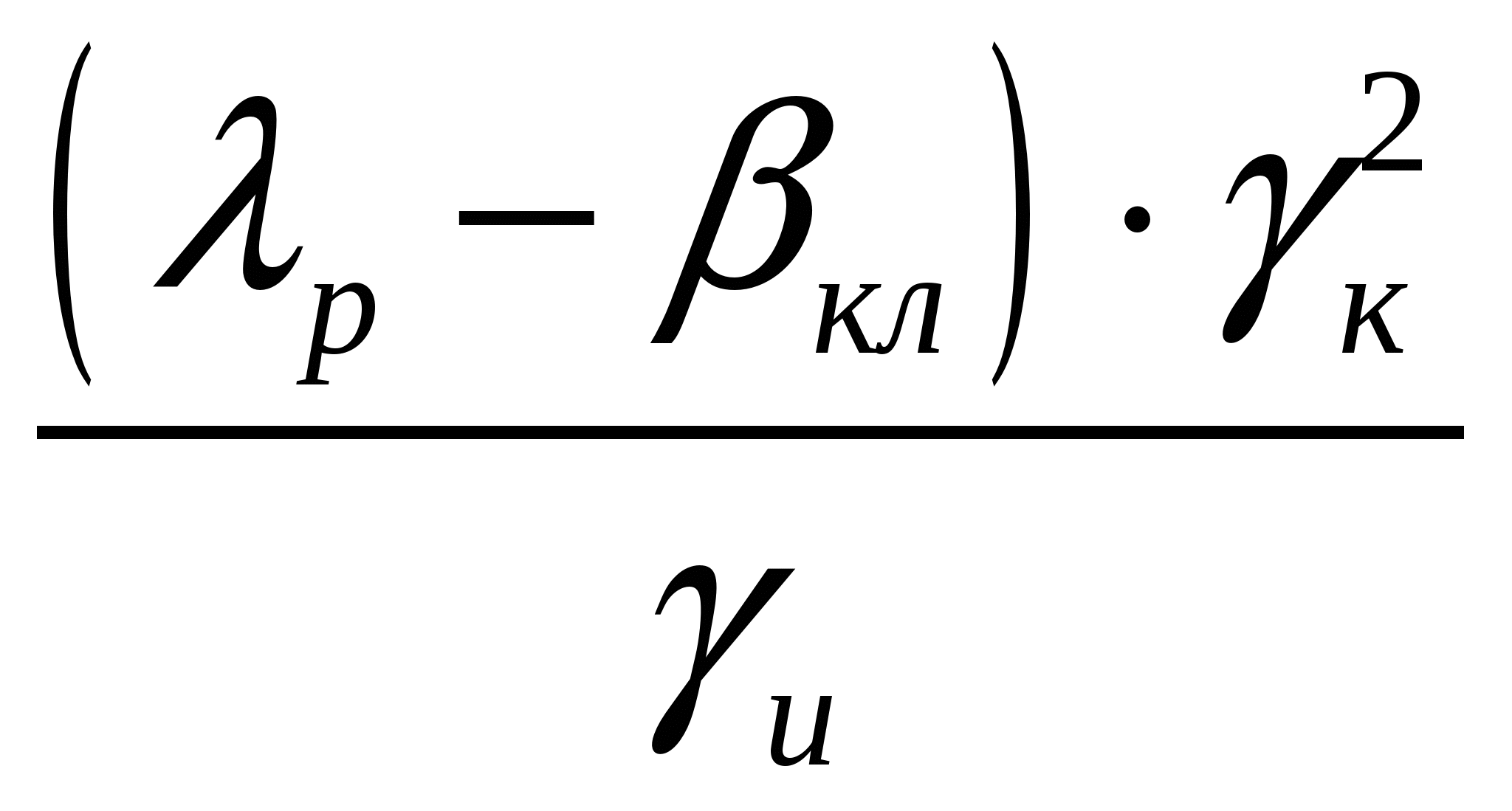 (4.12) (4.12)и хвостам 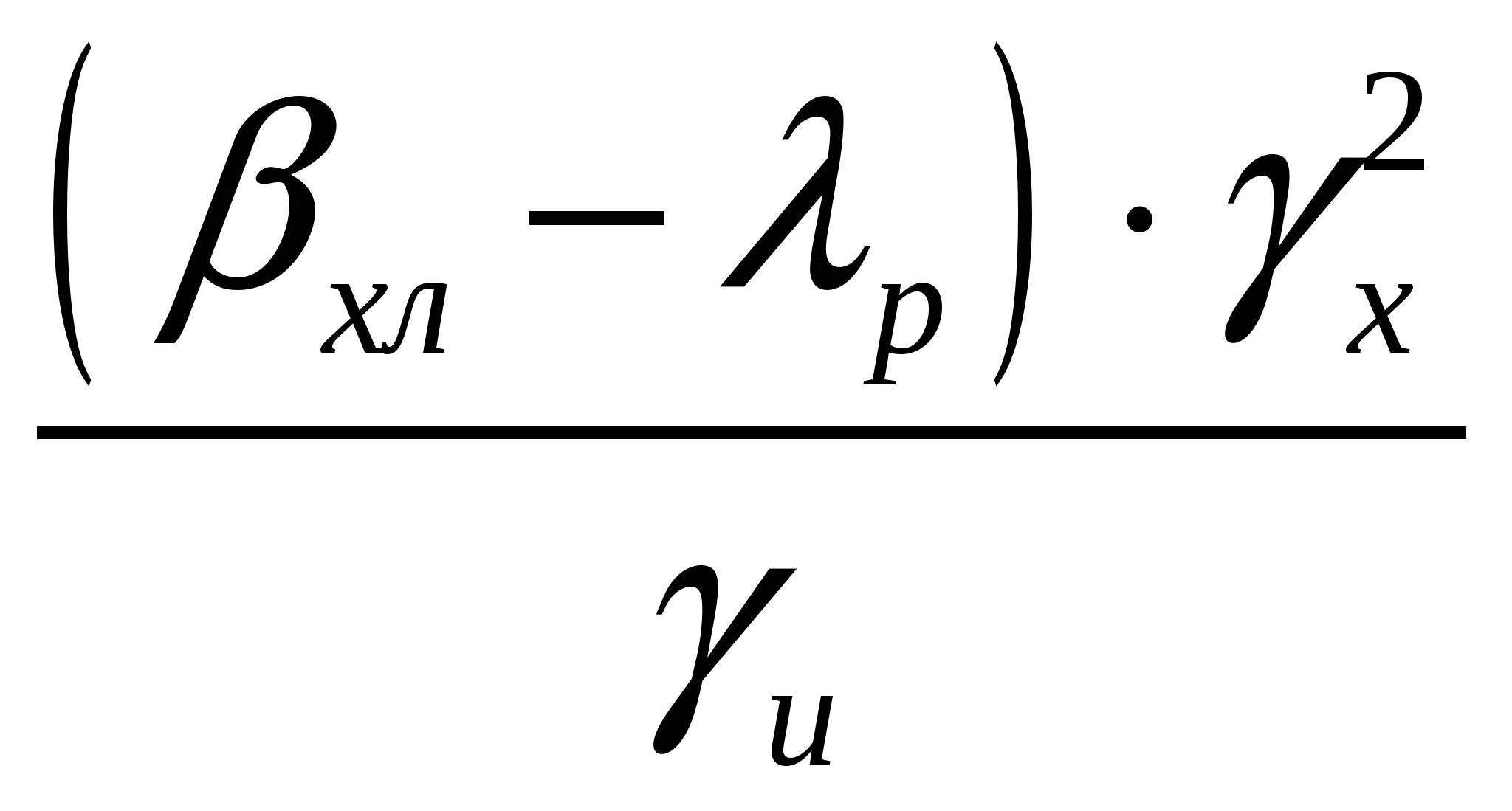 . (4.13) . (4.13)Группируя подобные члены, в окончательном виде получим более совершенный показатель “нормированной селективности” - показатель избирательности процесса сепарации I [24], 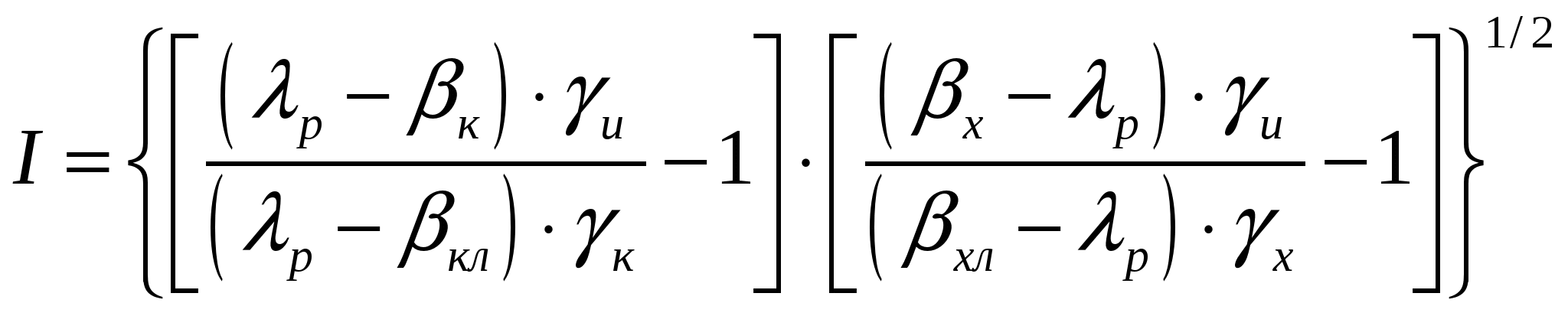 . (4.14) . (4.14)Ожидаемое преимущество этого критерия перед (2.13) – повышение его чувствительности к оцениваемым параметрам в два раза. Полученные по формулам (2.13) и (4.14) значения Θ и I для экспериментов, представленных рис. 4.6, 4.19 и 4.23, даны табл. 4.2. Таблица 4.2 Оценка сепарации критериями Θ и Iв разных экспериментах
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
