4КУрс_ОпКонсМод. Конспект лекций по дисциплине "моделирование обогатительных процессов" для специальности 090302 "Обогащение полезных ископаемых"
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
Таблица 2.2Зависимость сепарабельности от напряжённости поля
Полученные результаты выявляют зависимость положения экстремума X4, от заданной величины р, гребень которой как X4, найденный по методике [11], даёт возможность настраивать электрические параметры сепаратора по заданному технологическому режиму. Для р=0,85 установлен оптимальный уровень напряжённости электрического поля X4=390 КВм-1. По коэффициенту наклона почти прямого гребня X4р, равному для обогащаемого сырья 272 КВм-1, и допустимой ошибке поддержания заданной зольности разделения р01 (принята по диапазону изменения от марки угля) найдена требуемая точность стабилизации напряжённости электрического поля X4доп=272 КВм-1, примерно 1% к оптимальной величине. Альтернативы целеориентированному моделированию нет. Контрольные вопросы.
Литература к лекции: [1], [9], [11] Для заметок к лекции № 2.4 Лекция 3.1 Интерполяция данных гранулометрического состава Рассматриваемые вопросы:
Входные параметры обогатительного процесса представлены массивом сепарабельных (раздельных) частиц материала различной крупности, зольности, содержания серы и других компонентов, увязываемых в единое описание с помощью характеристик ситового и фракционного составов в форме таблиц. При этом рассматривают три дискретных функции: распределения зольностей F(λ), как производную от предыдущей функцию плотности распределения вероятностей зольности φ(λ) [7, 8], где λ – зольность элементарной фракции как функция от плотности D , λ=f(D), и распределения извлечений фракций по золе [9], см. (2.5). “В современном углеобогащении существует необходимость нахождения такого способа задания гранулометрического состава, который был бы универсален, т.е. чтобы его можно было применять для различных задач технологии” [10]. Информативность массива данных зависит от количества элементов (длины) этого массива. Непрерывная функция содержит максимум информации о представляемом ею явлении. Прогнозом называют определение функций распределения ситовых и фракционных показателей продуктов процесса сепарации и их характеристик по принципу практической уверенности [11] на основании табличных (дискретных) данных фракционно-ситового состава перерабатываемого материала в текущий момент времени. Существует ряд принципов и методов оценивания массивов, функций, решений. Принцип практической уверенности: “Событие, вероятность которого близка к единице, называют практически достоверным, а событие, вероятность которого близка к нулю, - практически невозможным” [11]. В применении к задаче интерполяции ситовой характеристики принцип практической уверенности позволяет обосновать решение нахождения новых опорных точек (НОТ) под названием knot-продолжения массива. Сущность метода продолжения массива данных ситового состава поясняется по схеме рис.3.1. Для упрощения изложения вопроса рассматриваются только 4 точки под номерами 0, 2, 4 и 6, которые названы узлами искомой зависимости. Пропущенные между ними точки с нечётными номерами 1, 3 и 5 зарезервированы для размещения распознаваемых НОТ-узлов. Рассмотрим построение точки типа 3 (рис. 3.1). Эта точка расположена внутри интервала 2 - 4 (и по аргументу, и по функции) и вблизи хорды 2 - 4. В отличие от кусочно-полиномиальной интерполяции, здесь вместо касательной слева от точки 2 строим хорду 0 - 2, а вместо касательной справа от точки 4 строим хорду 4 - 6. Продолжения хорды 0 - 2 и хорды 4 - 6 при пересечении образуют точку p, которая вместе с точками 2 и 4 создаёт “треугольник правдоподобия” (2, 4, p), окаймляющий область, по которой проходит гипотетическая кривая. 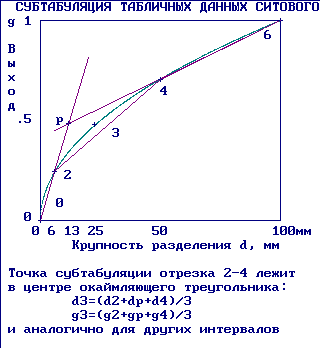 Рис.3.1. Схема определения новой опорной точки 3 массива данных. Треугольник полностью определён своими вершинами, так что полностью определён и его центр тяжести (2, 4, p) как НОТ, положение которого не зависит не только от масштабов переменных, но и от их размерностей. Метод доверительного треугольника работает только на выпуклой или вогнутой функции, что проверяется попаданием точки p в интерполируемый интервал как по аргументу, так и по функции. Выполнив такие расчёты для всех n0-1 интервалов, где n0 - количество исходных узлов интерполяции, получим НОТ первой рекурсии в количестве n1 = 2n0-1. Весь алгоритм представлен пунктами:
10) печать результатов; конец.  Пример. Для данных ситового анализа (табл. 3.1) требуется найти НОТ внутри интервалов данных. Расчёт выполнялся на ЭВМ. Пример. Для данных ситового анализа (табл. 3.1) требуется найти НОТ внутри интервалов данных. Расчёт выполнялся на ЭВМ.Таблица 3.1 Исходные данные ситового состава угля.
После выполнения i рекурсий количество узлов составит величину Ni= 2i(N0-1)+1. Результаты даны рис.3.2.  Таким образом, рекурсивный метод knot – продолжения массива данных ситового состава не требует поиска функций для описания массива внутри интервалов данных и обеспечивает монотонность интерполированных характеристик при любой закономерности распределения крупности угля. С решением задачи оптимальной минимизации набора сит при выполнении ситового анализа угля в производственных условиях ОФ можно ознакомиться в работе [8]. Контрольные вопросы: 1. Каким параметром определяется информативность масива данных сепарабельности?
Литература к лекции: [7, …, 11] Для заметок к лекции № 3.1 Лекция 3.2 Интерполяция данных фракционного состава Рассматриваемые вопросы:
Фундаментальные исследования вопросов описания характеристик обогатимости полезных ископаемых в значительной степени обобщены в монографии Верховского И. М. [1]. Там, со ссылкой на работу Maclarren W. [12], дан метод разложения одной широкой фракции-прямоугольника на две узкие фракции-трапеции. Достоинство метода описания фракционных характеристик по Maclarren W. [1] состоит в фиксации концов 2-кусочно-линейной функции. Схема решения задачи дана рис. 3.3. 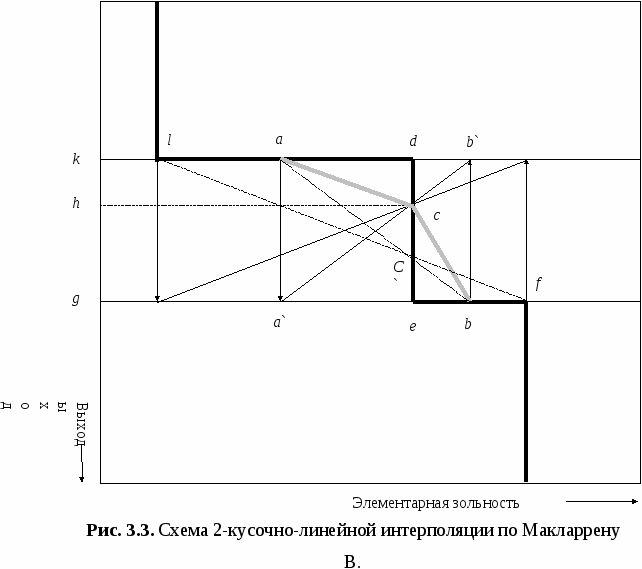   В расчётной схеме ступенька интерполируемой фракции обозначена ломаной ldef, а интерполирующая 2-кусочно линейная функция представлена отрезками ac и cb, так что точка c - это искомая точка интерполяции, которая единственным образом и определяет интерполирующую функцию. Посредине отрезка ld наносится точка a и на таком же расстоянии от оси ординат на отрезке gf отмечается точка a`. Аналогичным образом назначаются точки b и b`. Точки a` и b` соединяются отрезком a`b`. Пересечение отрезка a`b` с отрезком be даёт искомую точку c. Ломаная acb рассматривается как аппроксимация ступенчатого графика более “плавной” линией из двух отрезков. Таким образом, метод Maclarren W. [12] вполне обоснован. Аналитическим методом отрезок dc может быть вычислен непосредственно по формуле Maclarren W. [1, 12]: 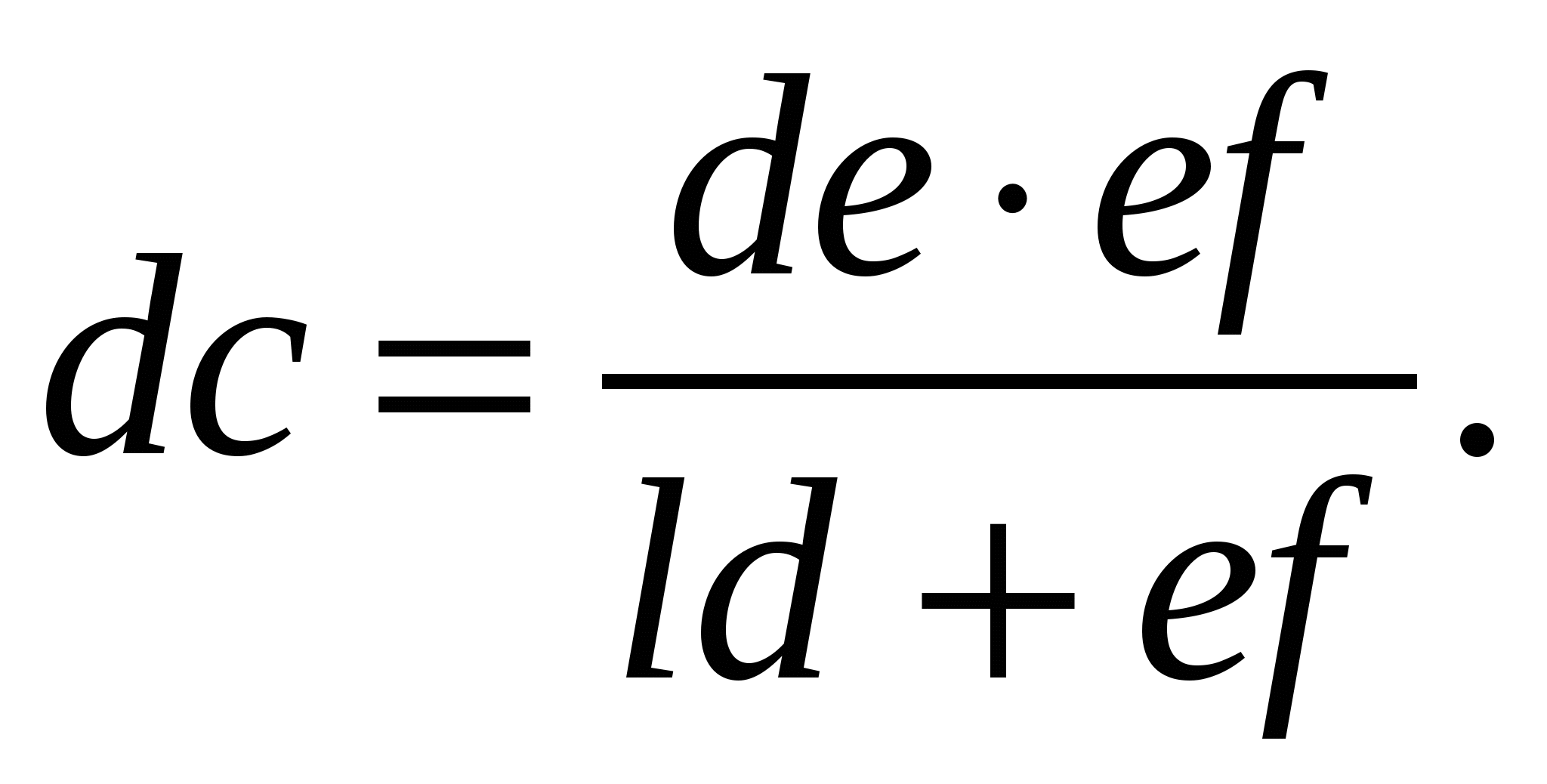 (3.1) (3.1)Затем следует полученные трапеции заменить эквивалентными прямоугольниками и к образованному таким приёмом новому массиву фракций снова применить процедуру удвоения размера массива и повторять её (продолжать методом рекурсии) до тех пор, пока количество фракций не достигнет требуемого минимума, например, 50. Результаты построения характеристик сепарабельности даны рис. 3.4. 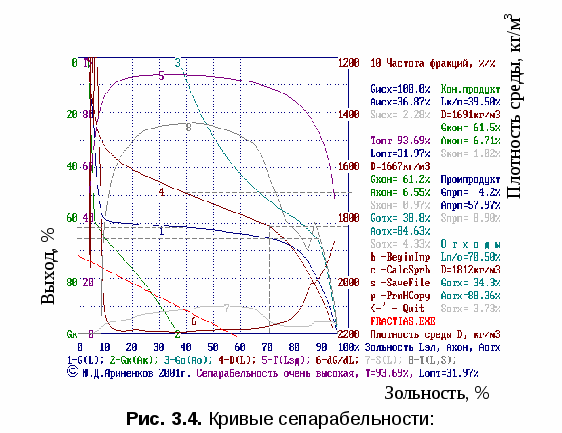 1 - зависимость выхода продукта от разделительной зольности; 2 - зависимость выхода кондиционного продукта от его зольности; 3 - зависимость выхода отходов от их зольности; 4 - зависимость плотности элементарных фракций от их зольности; 5 - теоретическая сепарабельность в функции зольности разделения; 6 - плотность распределения вероятности зольности фракций; 7 - зависимость содержания серы от их зольности; 8 - теоретическая сепарабельность в зависимости от зольности и серы. Контрольные вопросы.
Литература к лекции: [1], [12] Для заметок к лекции № 3.2 Лекция 3.3 Совместное описание фракционно-ситового состава Рассматриваемые вопросы: Сущность метода совместного описания ситового и фракционного составов. Идея и метод форматирования массивов данных сепарабельности для автоматизированного ведения электронной базы данных сепарабельности углей и шихтовки углей. Характеристики сепарируемого полезного ископаемого зависят от конкретных источников и доли их участия в поставке сырья. Автоматизированное ведение базы таких характеристик сдерживается проблемой композиции массивов данных несовпадающих размеров, для решения которой необходимо применить элементы алгебры множеств, теории отображений и отношений толерантности числовых функций [13]. Толерантность числовых функций фракционного и ситового массивов гарантирована методикой опробования сырья. Вопроса форматирования массива данных сепарабельности предваряется представлением такой характеристики [8, 14] рис.3.5. 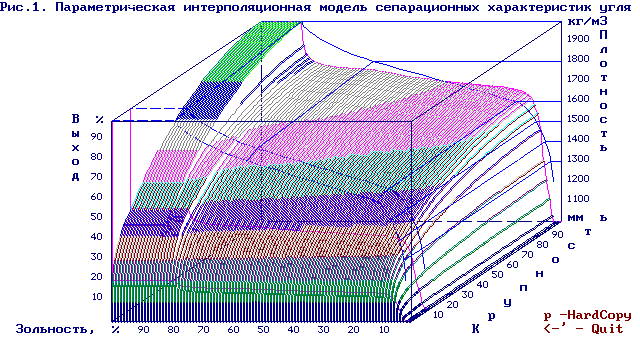 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
