4КУрс_ОпКонсМод. Конспект лекций по дисциплине "моделирование обогатительных процессов" для специальности 090302 "Обогащение полезных ископаемых"
 Скачать 0.67 Mb.
|
Рис. 1.2. Блок-схема соединения аппаратов обогатительной фабрики.На этой схеме объекты технологии (модели технологических процессов) представлены нумерованными прямоугольниками, входы которых обозначены горизонтальными линиями, а выходы – вертикальными. Необходимо учитывать, что деление точной схемы соединения процессов (см. рис.1.2) на схемы по видам расчёта разрушает связи между этими схемами. В металлургии чугуна известно, что повышение зольности шихты на 1% снижает спекаемость шихты по индексу вспучивания на 4,9 мм и прочность кокса по остатку в барабане на 4,6 кг. Повышение зольности кокса на 1% увеличивает его расход на 12 кг/т чугуна, что в итоге снижает производительность доменной печи на 2%. Вместе с тем, традиционные методы прогноза результатов обогащения на обогатительных фабриках допускают методическую ошибку в определении выхода продуктов до 10% и не определяют причину её появления. Эта ошибка порождена не только несоответствием представлений о свойствах прогнозирующей функции (часто это кривая Тромпа как аппроксимация интегральной функцией нормального распределения) и результатах её применения, но и метода расчёта сложных технологических схем. Контрольные вопросы.
Литература к лекции: [1], [3] Для заметок к лекции № 1.4 Лекция № 2.1 Дифференцирование сепарационных функций Рассматриваемые вопросы: Сепарабельность как свойство сыпучего материала. Показатель сепарабельности. Правило дифференцирования функции зольности продукта. Современная углеобогатительная фабрика характеризуется совокупностью множества взаимосвязанных процессов с определённой целенаправленностью и сложностью функционирования при условии удовлетворения многофакторной целевой функции, т.е. имеет признаки большой системы, для описания которой нужен критерий. Далее приняты следующие определения: 1) сепарабельность – это способность массива частиц материала к разделению на два массива по заданному физическому признаку; 2) показатель сепарабельности – это мера отделимости компонентов смеси частиц сыпучего материала по заданному признаку. Поиск условия оптимальности по модели с применением показателя сепарабельности связано с дифференцированием неявных функций сепарабельности. Традиционно дифференцирование таких функций (например, зависимости зольности продукта от его выхода) выполняют в конечных отклонениях, что снижает информативность получаемого результата. Для решения оптимизационных задач рекомендуется применять правило дифференцирования сепарационных функций, имеющих интегральное содержание. В основах теории обогатительных систем связи между элементарными и суммарными характеристиками устанавливаются зависимостью 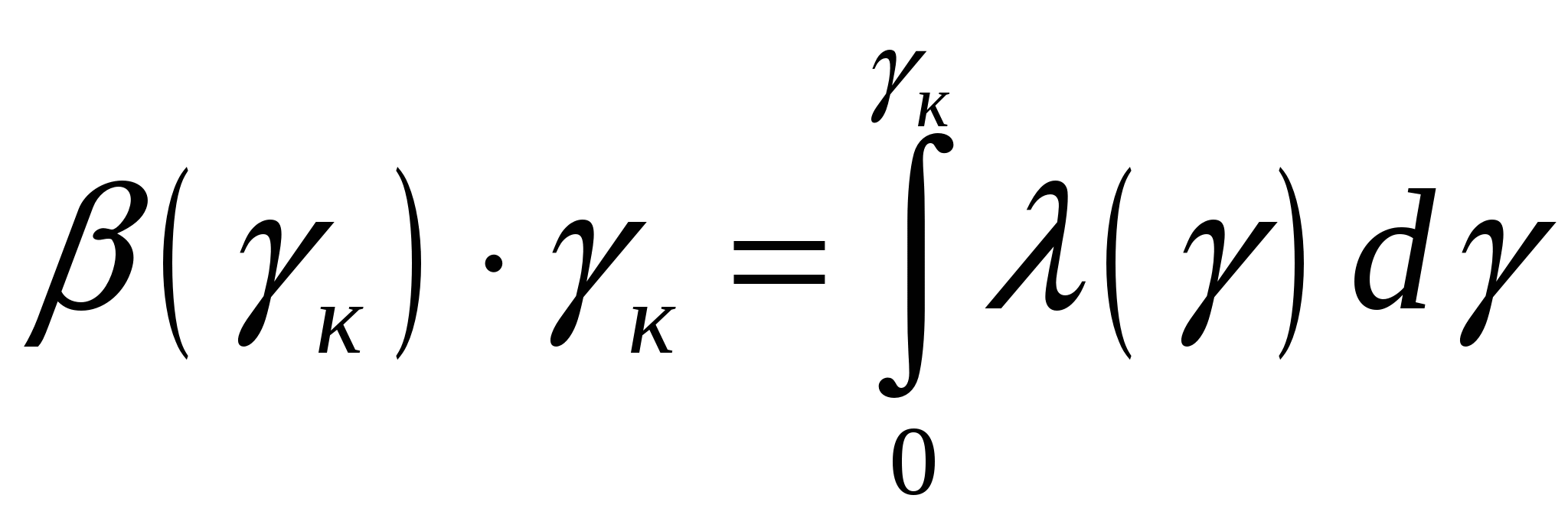[1]:  , (2.1)где к - выход обогащённого продукта; (к) - зольность обогащённого продукта как функция его выхода; () – функция обратная к распределению зольности фракций. В обогатительной практике с физической точки зрения в выражении (2.1) аргументом является не выход продукта обогащения , а элементарная зольность , которая связана с плотностью фракции D. Для обращения указанной зависимости следует сумму интегралов прямой () и обратной () функций приравнять площади прямоугольной области интегрирования этих функций, равной произведению ∙ . В интегральном исчислении подобное соотношение называют методом «интегрирования по частям», в применении к обогатительным процессам открывающее возможность принять в качестве аргумента зольность элементарной фракции (D), которая связана уже с плотностью разделения Dр. Если смысл интеграла функции () объясняется как количество золы в полученном продукте и (2.1) определяет средневзвешенную зольность продукта, то функция () есть распределение фракций , а её интеграл - оценка этого распределения. Рассмотрим левую часть (2.1). Это произведение неявно представленной функции зольности продукта β(γ) и её аргумента γ. Правая часть (2.1) представляет собою определённый интеграл, производная которого равна подинтегральной функции. Дифференцирование (2.1) по с учётом правила дифференцирования произведения функций приводит к зависимости [2]: 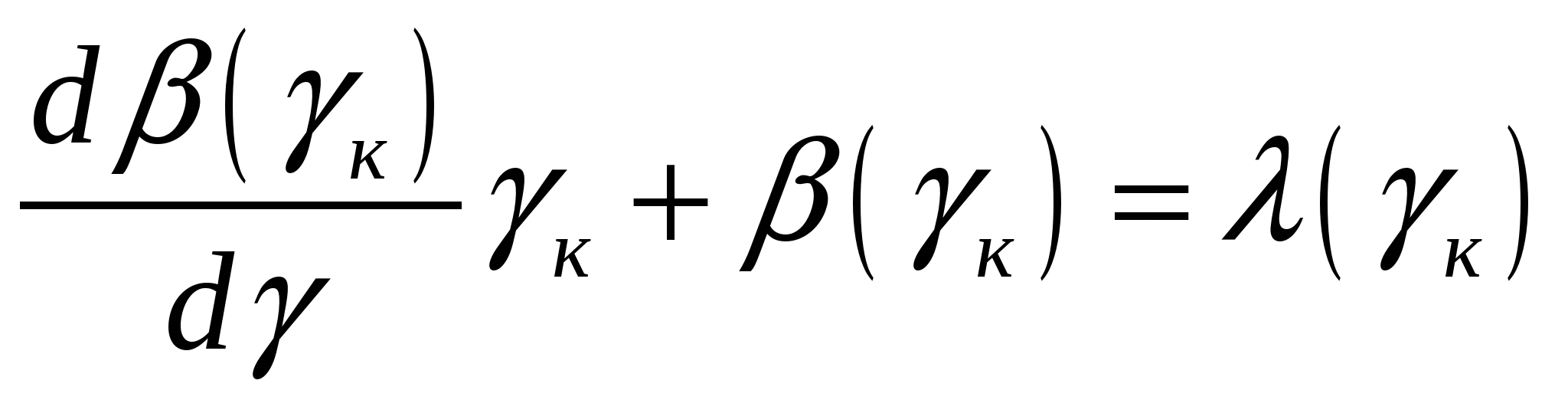  . (2.2)Здесь приписной символ к обозначает, что производная взята по правому пределу интегрирования, определяющему выход кондиционного продукта γк. Отсюда перегруппировкой членов получаем 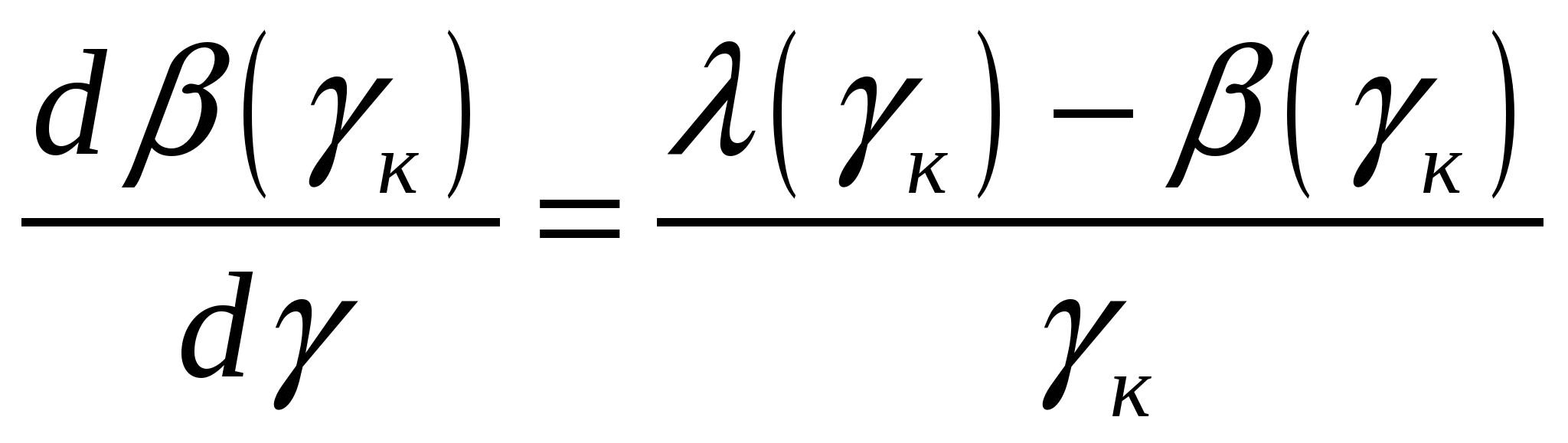[2, 3]:  . (2.3)Дифференцирование обогатительных (сепарационных) функций в конечных приращениях ведёт к потере существенной информации. Например, извлечение фракций в концентрат (функция Тромпа) в традиционном определении через конечные приращения как  , (2.4)при Δλ→0 имеющее  , интерпретируется отношением производных от выхода концентрата и от выхода исходного по параметру λ: , (2.5)где fи  , fк -плотности распределения золы исходного и концентрата.Из формулы (2.5) видно, что в общем случае кривая Тромпа не симметрична (в разделительной точке извлечение εр≠0,5). Следовательно, применение (2.3) вместо дифференцирования в конечных приращениях при исследовании эффективности сепарации сохраняет существенную информацию о взаимосвязях параметров сепарационного процесса. Контрольные вопросы.
Литература к лекции: [1] Для заметок к лекции № 2.1 Лекция 2.2 Условия оптимальности процесса сепарации Рассматриваемые вопросы: Принцип и метод оценки экономической эффективности обогащения углепродуктов. Принцип определения точки оптимальности сепарации по золе и сере. Метод оценки экономической эффективности основан на принципе линейных скидок, суть которого заключается в том, что устанавливается прейскурантная цена на продукт прейскурантного качества и назначается коэффициент скидок к этой цене K% за каждый процент ухудшения качества концентрата [4]. Цена продукта определяется уравнением плоскости на прейскурантной точке качества продукта: 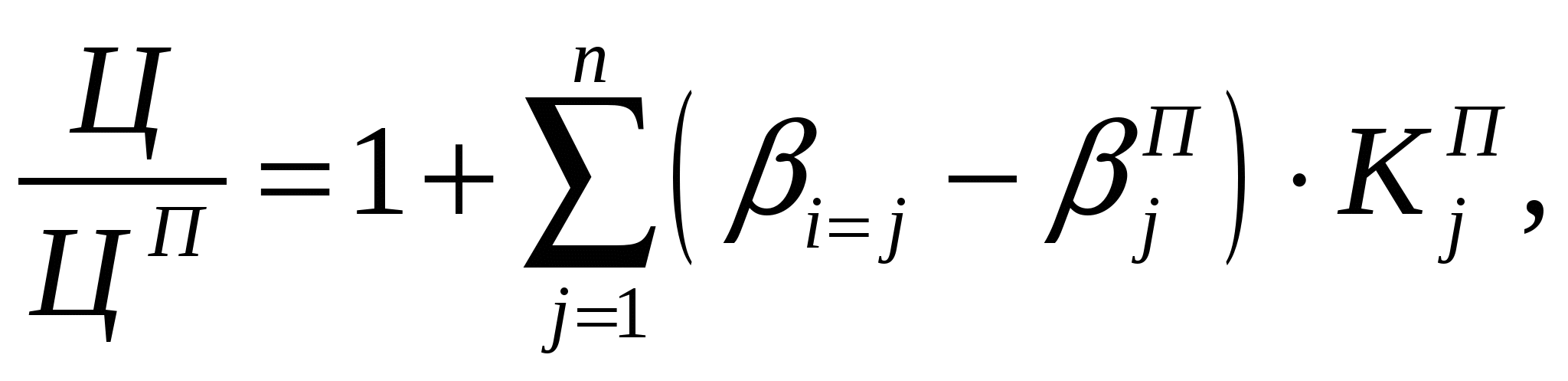 j=1, , n, (2.6) где jП - прейскурантное значение содержания j-го компонента; i=j - содержание i-го оцениваемого компонента; КjП - прейскурантный коэффициент надбавок за j -компонент; ЦП - прейскурантная цена; Ц - цена концентрата.Требуется найти условия, при которых стоимость продукта будет максимальной. С целью упрощения описания плоскости цены представим её в отрезках на осях системы ценообразования, рис. 2.1. 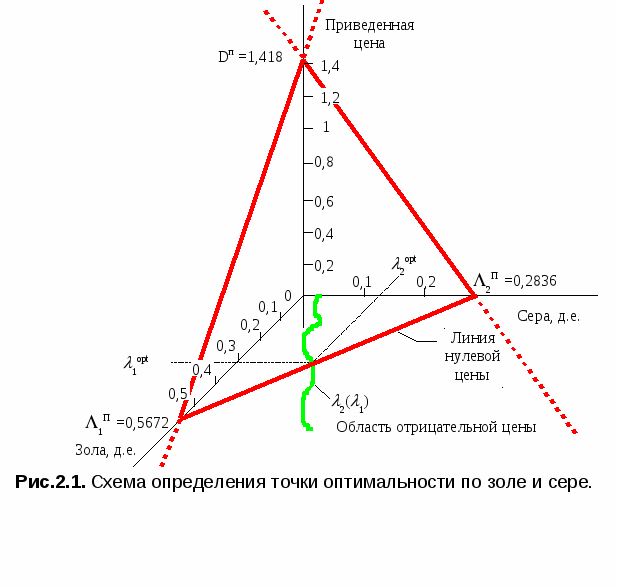 Для перехода к отрезкам на осях системы ценообразования введём обозначения приведенной цены  (2.7)и её свободного члена (Y при нулевых значениях всех аргументов i=0) 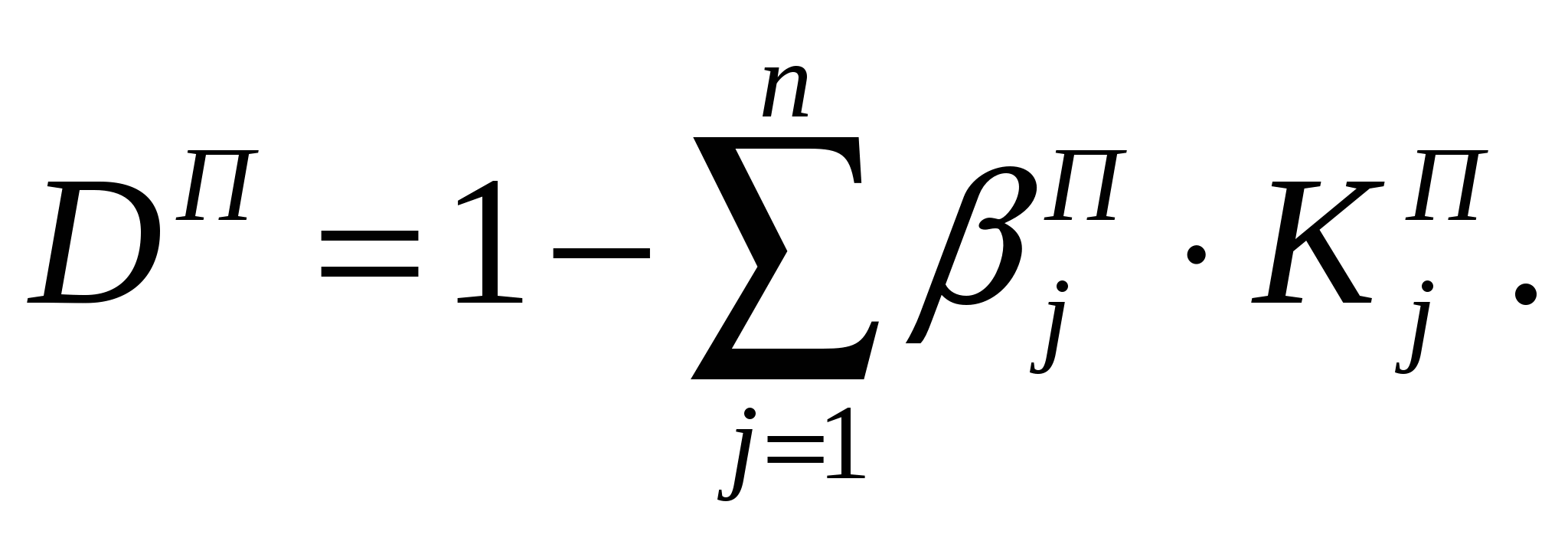 (2.8)Положив далее Y=0 для любого j при всех ij = 0, с учётом принятых обозначений из (2.6) получим прейскурантный отрезок Λjп на оси (j=i)-компонента, фиксирующий точку, через которую проходит плоскость цены,  (2.9)Плоскость цены продукта в отрезках на осях (рис. 2.1) построена по (2.8) и (2.9). Теперь запишем уравнение плоскости приведенной цены (2.7) в этих отрезках на осях аргументов jП как [5] 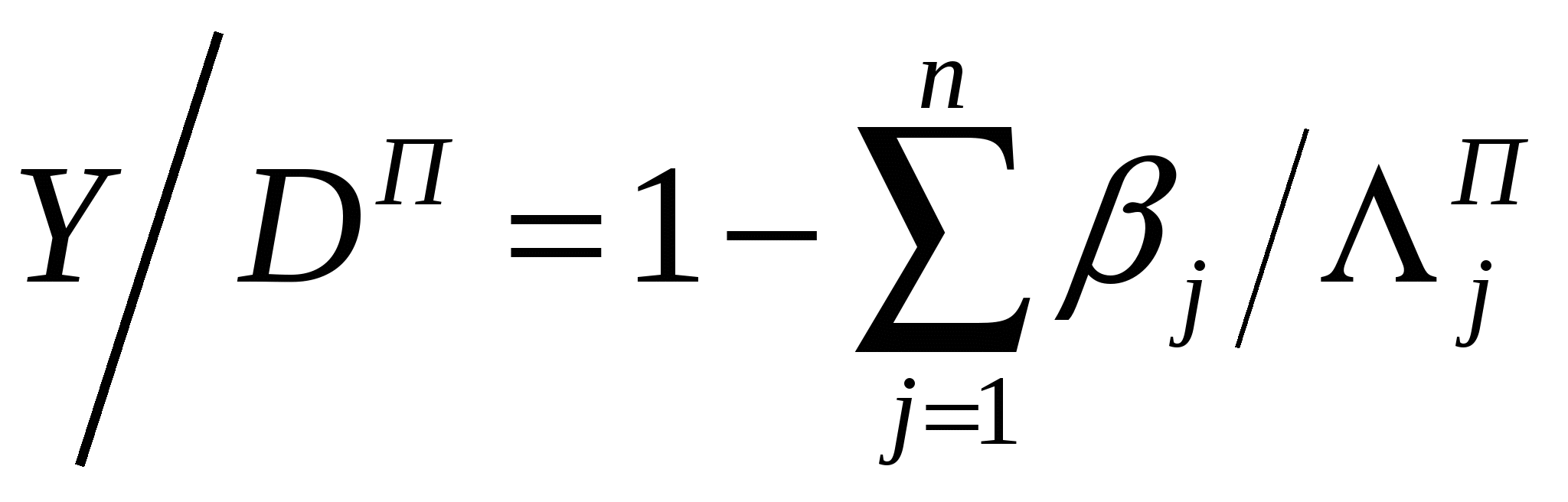 (2.10)и, соответственно (2.7), приведенную стоимость продукта, полученного из единицы исходного материала,  (2.11)где V - приведенная стоимость продукта, безразмерная величина; - выход продукта, доли единицы. Для нахождения условия максимальной стоимости продукта дифференцируем функцию стоимости из (2.11): 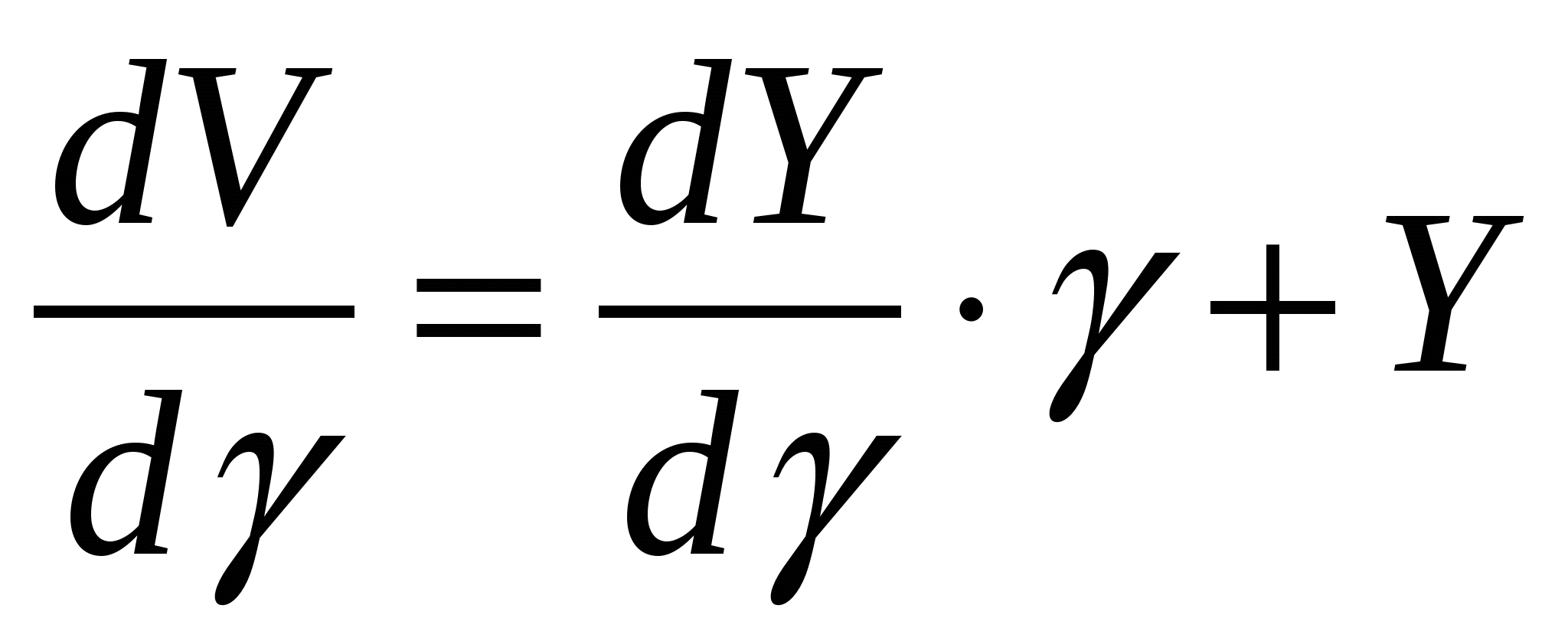 .Раскрывая здесь Y через (2.10) и (2.9) и дифференцируя его, находим 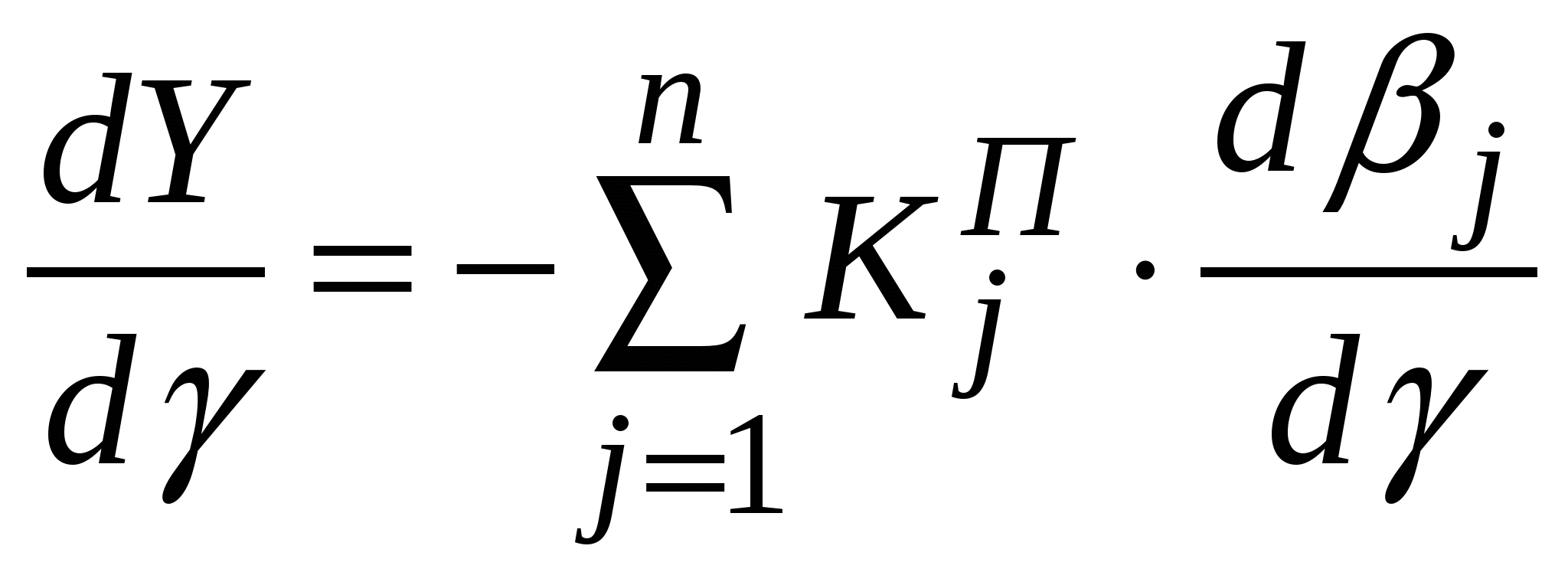 . |