Конспект лекций РиКМОНГП. Конспект лекций по дисциплине Расчет и конструирование машин и оборудования нефтяных и газовых промыслов Для специальности
 Скачать 2.08 Mb.
|
|
4.4 Методы расчета на прочность Расчеты на прочность выполняются с целью определения размеров и формы деталей машин, исключающих возможность их поломок и недопустимых деформаций в условиях нормальной эксплуатации. Различают проектные и проверочные расчеты на прочность. Проектные расчеты служат для определения наиболее характерных размеров, необходимых для начала проектирования детали. Полученные в результате проектных расчетов размеры только в простейших случаях могут оказаться окончательными. В большинстве же случаев размеры и форма деталей изменяются при дальнейшем их согласовании с конструктивными требованиями проектируемой машины и действующими стандартами. Окончательные размеры, форма опасных сечений, шероховатость поверхности и другие факторы, влияющие на конструкционную прочность детали, определяются при деталировке проектируемой машины. Проверочные расчеты, позволяющие оценить конструкционную прочность детали путем сопоставления расчетных запасов прочности с допустимыми, выполняются при деталировке машины. Если расчетные запасы прочности оказываются меньше допустимых, вносятся необходимые конструктивные и технологические изменения, повышающие прочность рассчитываемой детали. За последние годы проделана большая работа по совершенствованию методов прочностных расчетов, в результате которой разработаны отраслевые нормы и правила расчета на прочность бурильных и обсадных труб, талевых канатов, втулочно-роликовых цепей, подшипников, валов и других деталей буровых машин и оборудования. Это позволило ускорить проектирование и одновременно устранить или повысить прочностные лимиты наиболее ответственных деталей и узлов буровых машин и оборудования. Применяемые методы прочностных расчетов имеют так называемый детерминистический характер, так как основаны на предположении, что расчетные нагрузки и параметры прочности имеют определенную (детерминированную) величину. Между тем нагрузки являются случайными функциями времени, а параметры прочности изменяются в определенных пределах, зависящих от однородности материала деталей, стабильности технологии изготовления и других факторов. Поэтому детерминистические методы прочностных расчетов в ряде случаев недостаточны. Более эффективны вероятностные методы расчета на прочность, распространенные в строительной механике и некоторых других областях техники. В этих расчетах нагрузки и прочностные свойства задаются законами их распределения, полученными на основе статистической информации, а запасы прочности устанавливаются в зависимости от планируемого уровня безотказной работы. Использование вероятностных методов прочностных расчетов затрудняется из-за отсутствия или недостаточного объема статистической информации, необходимой для выявления законов распределения нагрузок и прочности деталей буровых машин и оборудования. Дальнейшее развитие методов прочностных расчетов буровых машин и оборудования связано с разработкой программ для вычислительных машин. С целью успешного решения этой задачи необходимо постоянно совершенствовать применяемые методы расчета, исходные зависимости которых являются общими для ручных и машинных расчетов. Важно отметить значение табличных методов расчета, используемых при ручном расчете. Овладение табличным методом способствует развитию операционного мышления и является необходимой предпосылкой разработки программ для вычислительных машин. 4.5 Расчеты на статическую прочность На статическую прочность рассчитывают детали, испытывающие постоянные либо медленно возрастающие нагрузки. Условия статической прочности в проектных расчетах имеют вид:  (7)В проверочных расчетах прочность деталей определяется по условиям:  (8)Здесь σ, τ —максимальные нормальные и касательные напряжения; σпр, τпр - предельные напряжения [Sσ], [Sτ] - допускаемые (нормируемые) коэффициенты запаса прочности; [σ], [τ] - допускаемые напряжения; Sσ, Sτ - действительные коэффициенты запаса прочности. Расчетные напряжения определяются по наибольшим нагрузкам. Для деталей вертлюга и других устройств, расположенных между крюком и подъемным валом лебедки, расчетные нагрузки определяют, исходя из допускаемой паспортной нагрузки на крюке. Детали, расположенные между подъемным валом и двигателями буровой лебедки, рассчитываются по максимальным крутящим моментам и нагрузкам, создаваемым действием привода подъемного механизма. Детали ротора и его трансмиссии рассчитываются по наибольшим значениям статической нагрузки и крутящего момента, заданным для стола ротора. Детали механической части буровых насосов рассчитываются по величине максимального крутящего момента, создаваемого приводом насоса. Расчет деталей гидравлической части буровых насосов ведется по заданному максимальному давлению. Расчетные напряжения деталей насоса определяются с учетом коэффициента перегрузки, принимаемого равным 1,7—2,5 (см. гл. XIV). Максимальные расчетные напряжения в зависимости от напряженно-деформированного состояния детали определяются по известным формулам:  При растяжении и сжатии где Pz — продольная (нормальная) сила растяжения ( + ) или сжатия (—), действующая в рассматриваемом сечении; F — расчетная площадь сечения; при сдвиге  где Рх, Ру — поперечные силы; при смятии  где Р — действующая сила; Fсм — площадь смятия; при изгибе  где Мизг — изгибающий момент в рассматриваемом сечении; Wизг — осевой (экваториальный) момент сопротивления сечения; при кручении  где Мк — крутящий момент в рассматриваемом сечении; Wк — полярный момент сопротивления сечения. Формулы для расчета площади и моментов сопротивления наиболее распространенных видов поперечного сечения валов и осей приведены в табл. 3. Для ответственных деталей обычно используются пластичные материалы и в качестве предельного напряжения принимается предел текучести. Для хрупких материалов предельное напряжение характеризуется пределом прочности. Конструкционные материалы делят на пластичные и хрупкие по результатам испытаний на разрыв и удар [7]: Таблица 4.3 Геометрические характеристики основных видов сечений валов и осей
Примечание: δ - относительное удлинение; φ - относительное сужение; ан - ударная вязкость. П 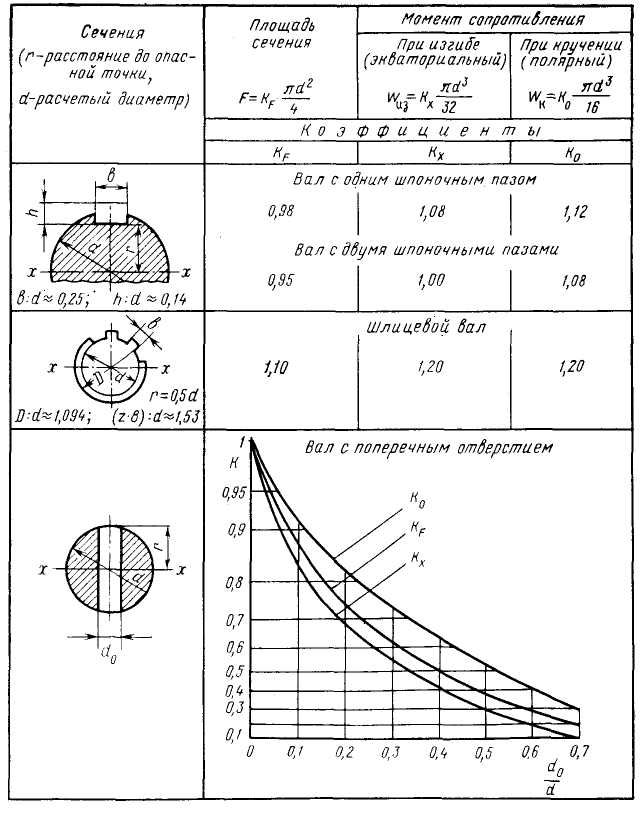 ри действии постоянных нагрузок концентрация напряжений не снижает прочности деталей из пластичных материалов, так как местные пластические деформации способствуют перераспределению и выравниванию напряжений в сечениях детали. В результате пластического течения в зонах концентрации напряжений наблюдается некоторое упрочнение материала. В связи с этим детали из пластичных материалов рассчитывают на статическую прочность по номинальным напряжениям. Детали из малопластичных материалов однородной структуры (легированные стали, стали, работающие при низких температурах) рассчитывают с учетом концентрации напряжений, вызывающих снижение прочности детали. Условие прочности при этом принимает вид: (9)где Kσs — эффективный коэффициент концентрации напряжений при статическом нагружении. В первом приближении значение Kσs принимается равным эффективному коэффициенту концентрации напряжений, используемому в расчетах на выносливость. Для хрупких материалов неоднородной структуры (чугун), обладающих пониженной чувствительностью к концентрации напряжений, расчет ведется по номинальным напряжениям. Коэффициенты запаса прочности, выражающие отношение предельных напряжений к действующим, определяют прочность и экономичность конструкции. Необоснованное завышение допускаемого коэффициента запаса прочности может привести к созданию неэкономичной конструкции и недостаточно прочной при заниженном его значении. Известны различные способы назначения коэффициента запаса прочности. Наиболее достоверные значения его могут быть определены на основе накопленного опыта проектирования и эксплуатации одинаковых либо подобных деталей. Согласно этому методу, разрабатываются нормы расчета и соответствующие им значения допускаемых коэффициентов запаса прочности. Для некоторых типовых элементов бурового оборудования (приводные роликовые цепи, талевые канаты, бурильные и обсадные трубы, валы и др.) нормативные коэффициенты запаса прочности приведены в табл. 1П приложения и последующих разделах, посвященных рассмотрению отдельных видов бурового оборудования. При отсутствии нормативных данных коэффициенты запаса прочности назначаются с учетом однородности материала ответственности детали и точности расчета. Согласно принятой в общем машиностроении методике, минимально допустимые значения запасов прочности определяются в зависимости от степени пластичности материала, характеризуемой отношением στ/σв.
Если действительные нагрузки и напряжения вычислены недостаточно точно, запасы прочности следует увеличить в 1,2— 1,5 раза [7]. Детали из малопластичных и хрупких материалов рассчитывают по пределу прочности, а минимально допустимые значения запаса прочности определяют в зависимости от однородности, степени хрупкости и остаточной напряженности используемых материалов. Для деталей из однородных хрупких материалов (ударная вязкость ан = 200÷300 кДж/м2) запас прочности [Sв] = 2÷3; для неоднородных хрупких материалов (ан = 50÷200 кДж/м2) при умеренных остаточных напряжениях запас прочности [Sв] = 3÷4 для весьма неоднородных и хрупких материалов (ан<50 кДж/м2) запас прочности [Sв]=4÷6. В случае недостаточной достоверности расчетов, и особенно при приближенной оценке уровня динамических нагрузок, указанные значения запасов прочности следует увеличить в 1,5-2 раза. При совместном действии нормальных и касательных напряжений (например, совместном изгибе и кручении) расчеты на прочность выполняются по эквивалентным напряжениям, определяемым согласно известным гипотезам прочности. В расчетах бурового оборудования обычно пользуются гипотезой наибольших касательных напряжений, согласно которой общий коэффициент запаса прочности 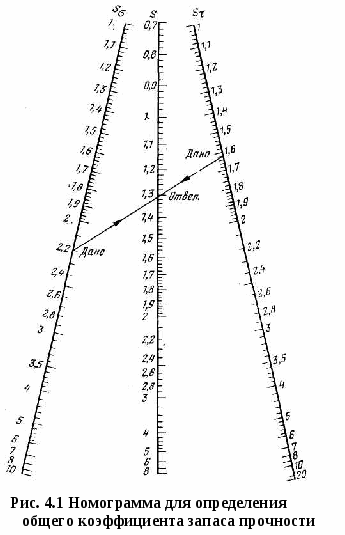  (10)На рис. 4.1 приведена номограмма для определения общего коэффициента запаса прочности в зависимости от частных его значений по нормальным и касательным напряжениям. Пример. Дано: Sσ = 2,2; Sτ=l,62. Ответ: по номограмме находим S = 1,3. 4.6 Расчет на прочность при переменных напряжениях Переменные напряжения в деталях машин различаются по виду циклов и характеру изменения цикла во времени. Циклом напряжений называют совокупность последовательных значений напряжений за один период их изменения при регулярном нагружении. На рис.4.2 показаны различные виды циклов переменных напряжений, характеризуемые следующими параметрами: с  реднее напряжение цикла, выражающее постоянную (положительную или отрицательную) составляющую цикла напряжения: (11)амплитуда напряжений цикла, выражающая наибольшее положительное значение переменной составляющей цикла напряжений:  (12)где σmах и σmin — максимальное и минимальное напряжения цикла, соответствующие наибольшему и наименьшему напряжениям цикла. Отношение минимального напряжения цикла к максимальному называют коэффициентом асимметрии цикла напряжений:  (13)Симметричным называется цикл, когда максимальное и минимальное напряжения равны по абсолютному значению и противоположны по знаку. Симметричный цикл является знакопеременным и имеет следующие параметры: σа = σmах = σmin; σт = 0; R = - 1. Наиболее распространенный пример симметричного цикла напряжений - изгиб вращающегося вала (изгиб при вращении). Пределы выносливости, соответствующие симметричному циклу, имеют индекс «—1» (σ-1; τ-1). Асимметричным называется цикл, у которого максимальное и минимальное напряжения имеют разные абсолютные значения. Для асимметричного цикла напряжений σmax = σm + σa; σmin = σm - σa; R ≠ - 1 Асимметричные циклы напряжений относятся к знакопеременным, если напряжения изменяются по значению и по знаку. Цикл напряжений, изменяющихся только по абсолютному значению, называется знакопостоянным. Пределы выносливости, соответствующие асимметричному циклу, обозначаются индексом «R» (σR; τR). Характерным асимметричным циклом является отнулевой цикл напряжений, к которому относятся знакопостоянные циклы напряжений, изменяющиеся при растяжении от нуля до максимума (σmin = 0) или при сжатии - от нуля до минимума (σmax = 0). При растяжении отнулевой цикл напряжений характеризуется следующими параметрами: σm=σa = σmax/2; R = 0. Предел выносливости отнулевого цикла обозначается индексом «0» (σ0; τ0). Отнулевые циклы напряжений возникают в зубьях шестерен и цепных звездочек, которые в процессе работы нагружаются при входе в зацепление и полностью разгружаются при выходе из него. С 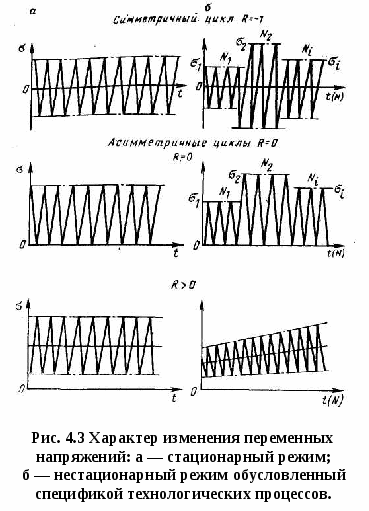 опротивление усталости зависит не только от вида действующих циклов напряжений, но и от характера изменения напряжений во времени. При стационарном нагружении значения амплитуды и среднего напряжения цикла остаются неизменными во времени. Буровые машины и оборудование, как уже отмечалось, преимущественно работают при нестационарном нагружении.Амплитуда и среднее напряжение циклов могут иметь ступенчатый либо непрерывный характер изменения (рис. 4.3). Количественные характеристики сопротивляемости материала действию переменных напряжений определяют путем испытания на усталость 15-20 одинаковых образцов диаметром 7-10 мм, имеющих полированную поверхность. Испытания проводят при разных уровнях напряжений. По полученным результатам строят график кривой усталости (рис. 4.4,а). По оси ординат графика откладывают максимальное напряжение или амплитуду напряжений цикла, при которых испытывался данный образец, а по оси абсцисс - число циклов N перемен напряжений, которое образец выдержал до разрушения. Полученная кривая характеризует зависимость между напряжениями и циклической долговечностью одинаковых образцов при постоянных среднем напряжении цикла либо коэффициенте асимметрии цикла. Для большинства сталей при испытаниях на воздухе кривая усталости, начиная с числа циклов N = 106÷107, становится горизонтальной и образцы, выдержавшие указанное число циклов, не разрушаются при дальнейшем практически неограниченном увеличении числа циклов нагружения. Поэтому испытания сталей прекращают при достижении 10 млн. циклов, составляющих базу испытаний Nб. Максимальное по абсолютному значению напряжение цикла, при котором еще не происходит усталостное разрушение до базы испытаний, называют пределом выносливости. Для надежной оценки предела выносливости число неразрушившихся образцов при данном уровне переменных напряжений должно быть не менее шести. Н 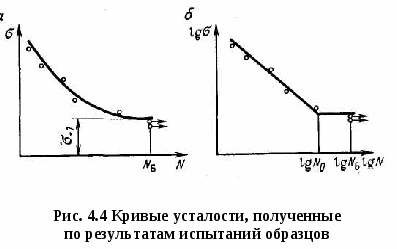 аиболее простыми и поэтому более распространенными являются испытания на усталость при симметричном цикле напряжений (круговой изгиб). Испытания на усталость при асимметричном цикле напряжений проводят на специальных испытательных машинах. Кривые усталости, построенные в логарифмических координатах (рис. 4.4,б), представляют собой наклонную и горизонтальную прямые. Для расчетов на прочность левую наклонную часть кривой усталости представляют в виде  (14)где σ - действующее напряжение; т - показатель наклона кривой усталости; N - число циклов напряжений, выдержанных до усталостного разрушения (циклическая долговечность); σ-1 - предел выносливости; N0 - число циклов, соответствующее точке перелома кривой усталости, представляемой двумя прямыми линиями. Величина N0 в большинстве случаев колеблется в пределах 106-3∙106 циклов. В расчетах на прочность при переменных напряжениях, когда отсутствуют данные усталостных испытаний, можно принять в среднем N=2∙106 циклов [33]. Показатель наклона кривой усталости  (15)для деталей изменяется от 3 до 20, причем с ростом эффективного коэффициента концентрации напряжений замечена тенденция к снижению т. Приближенно можно принять  (16)где с=12 - для сварных соединений; с= 12÷20- для деталей из углеродистых сталей; с = 20÷30 - для деталей из легированных сталей. Рекомендуемые значения показателя т и число циклов N0, соответствующее точке перелома кривой усталости, приведены в табл. 4.4. Таблица 4.4
Из уравнения кривой усталости определяется циклическая долговечность N при действии напряжений σ, превышающих предел усталости σ-1  (17)Значения пределов выносливости, полученные в результате испытаний на усталость, даются в справочниках по машиностроительным материалам. Соотношения между пределами прочности и выносливости, установленные на основе статистических данных приведены в табл. 4.5. Таблица 4.5
Предел выносливости деталей ниже предела выносливости стандартных лабораторных образцов, используемых при испытании машиностроительных материалов на усталость. Снижение предела выносливости обусловлено влиянием концентрации напряжений, а также абсолютных размеров поперечного сечения и состояния поверхности деталей. Значения предела выносливости деталей определяются путем натурных испытаний либо по справочным расчетно-экспериментальным данным, устанавливающим влияние указанных факторов на сопротивление деталей усталости. Натурными испытаниями обычно пользуются для определения пределов выносливости широко распространенных стандартных изделий и отдельных наиболее ответственных узлов и деталей. Так, на основе натурных испытаний установлены пределы выносливости бурильных труб, втулочно-роликовых цепей буровых установок, талевых канатов, подшипников и некоторых других стандартных изделий, применяемых в буровых машинах и оборудовании. В связи со сложностью натурных испытаний на усталость в практических расчетах на прочность преимущественно пользуются расчетно-экспериментальными данными, на основе которых предел выносливости детали определяется из выражения  (18)где σ-1д — предел выносливости детали; σ-1 - предел выносливости стандартных лабораторных образцов из материала детали; К - коэффициент снижения предела выносливости:  (19)Здесь Кσ - эффективный коэффициент концентрации напряжений; КF- коэффициент влияния шероховатости поверхности; Кd- коэффициент влияния абсолютных размеров поперечного сечения: Kυ - коэффициент влияния поверхностного упрочнения. Значения эффективных коэффициентов концентрации напряжений и коэффициентов влияния поверхностного упрочнения, полученные по расчетно-экспериментальным данным, приведены в табл. 4.1 и 4.2. Коэффициент влияния абсолютных размеров поперечного сечения определяется отношением предела выносливости гладких образцов диаметром d к пределу выносливости гладких лабораторных образцов диаметром 7-10 мм:  (20)где σ-1d - предел выносливости гладкого образца (детали) диаметром d; σ-1 - предел выносливости материала, определяемый на стандартных гладких образцах диаметром 7-10 мм. Опытные данные показывают, что с увеличением поперечных размеров предел выносливости детали снижается. Это объясняется статистической теорией усталостных разрушений, согласно которой при увеличении размеров возрастает вероятность наличия в деталях внутренних дефектов в зонах повышенных напряжений - масштабный эффект. Проявлению масштабного эффекта способствуют ухудшение однородности материала, а также трудность контроля и обеспечения стабильности процессов изготовления деталей больших размеров. Масштабный эффект зависит главным образом от поперечных размеров и в меньшей мере от длины детали. В 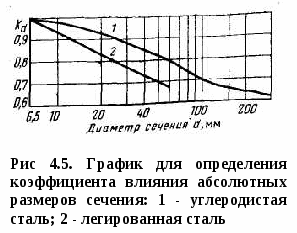 литых деталях и материалах, имеющих неметаллические включения, поры и другие внутренние и внешние дефекты, масштабный эффект проявляется больше. Легированные стали более чувствительны к внутренним и внешним дефектам, и поэтому для них влияние абсолютных размеров проявляется значительнее, чем для углеродистых сталей. В расчетах на прочность значения коэффициентов влияния абсолютных размеров поперечного сечения выбираются по графику (рис.4.5).Шероховатость поверхности, окалины и коррозия существенно влияют на сопротивление усталости. На рис. 4.6 показан экспериментальный график, характеризующий изменение предела выносливости деталей при различном качестве обработки и состоянии поверхности. Коэффициент влияния шероховатости определяется отношением предела выносливости гладких образцов с поверхностью не грубее Ra = 0,32 по ГОСТ 2789-73 к пределу выносливости образцов с данной шероховатостью поверхности:  (21)где σ-1 - предел выносливости тщательно полированных образцов; σ-1п - предел выносливости образцов с данной шероховатостью поверхности. Например, установлено, что при грубом шлифовании предел выносливости детали из стали с пределом прочности 1500 МПа оказывается таким же, как у стали с пределом прочности 750 МПа. Влияние состояния поверхности детали на сопротивление усталости обусловлено высоким уровнем напряжений от изгиба и кручения в наружных зонах детали и ослаблением поверхностного слоя вследствие его шероховатости и разрушения кристаллических зерен при резании. П 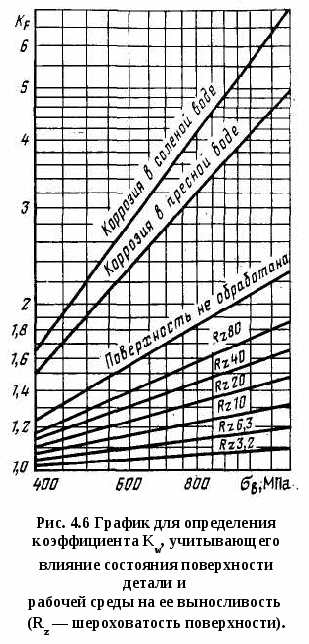 о аналогичным формулам определяются пределы выносливости деталей при действии касательных напряжений.Условия прочности при симметричном цикле переменных напряжений имеют вид: при действии нормальных напряжений  (22)при действии касательных напряжений  (23)где пσ, пτ - коэффициенты запаса прочности по нормальным и касательным напряжениям; σ-1д, τ-1д - пределы выносливости детали; σа, τа - амплитуды переменных напряжений; [пσ], [пτ] - минимально допустимое значение запаса прочности по нормальным и касательным напряжениям. При двухосном напряженном состоянии, возникающем в случае одновременного изгиба и кручения или растяжения-сжатия и кручения, запас прочности в расчетном сечении определяется из выражения 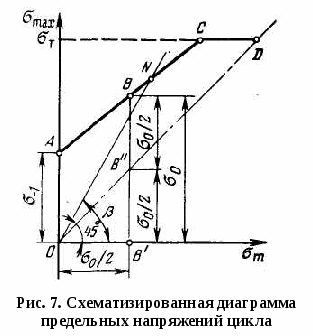 (24)М  инимально допустимое значение запаса прочности зависит от точности выбора расчетных нагрузок и полноты учета конструктивных, технологических и эксплуатационных факторов, влияющих на предел выносливости детали. В расчетах буровых машин и оборудования на выносливость минимально допустимые значения запасов прочности регламентируются отраслевыми нормами, указанными в табл. 2П приложения. При отсутствии отраслевых норм принимают допустимые запасы прочности [п]= 1,3÷1,5.При действии асимметричных циклов детали рассчитывают на прочность на основе диаграммы предельных напряжений цикла (рис. 4.7), характеризующей зависимость между предельными напряжениями и средними напряжениями цикла для заданной долговечности. Диаграмма строится по экспериментальным значениям пределов выносливости, полученным для различных средних напряжений цикла. Это требует длительных испытаний по специальной программе. В практических расчетах используются более простые схематизированные диаграммы предельных напряжении, которые строят по экспериментальным значениям предела выносливости симметричного и отнулевого циклов и пределу текучести выбранного материала. На диаграмме предельных напряжений точка А (0, σ-1) соответствует пределу выносливости симметричного цикла, точка В (σ0/2; σ0) - пределу выносливости отнулевого цикла напряжений. Прямая, проходящая через эти точки, определяет максимальные предельные напряжения, циклов в зависимости от среднего напряжения. Напряжения ниже уровня ABC не вызывают разрушения при числе циклов N0, соответствующем базе испытаний. Точки, лежащие выше прямой ABC, характеризуют циклы напряжений, при которых разрушение происходит при числе циклов N Прямая ABC, ограниченная в верхней части пределом текучести σт, т. е. сопротивлением пластическим деформациям, называется линией предельных напряжений. Она выражается уравнением прямой, проходящей через две точки А и В с координатами (0, σ-1) и (σ0/2; σ0):   Обозначив получим  (25)При действии касательных напряжений формула (25) примет вид  (26)Коэффициенты φσ и φτ характеризуют чувствительность материала к асимметрии цикла напряжений соответственно при действии нормальных и касательных напряжений (принимаются из технической литературы). Если на диаграмме провести из начала координат прямую под углом 45° (биссектрису координатного угла), то отрезок ОВ' == ВВ'-ВВ" будет соответствовать среднему напряжению, а отрезок ВВ" - предельной амплитуде цикла  (27)где σа - предельная амплитуда цикла, т. е. амплитуда напряжения, соответствующая пределу выносливости при заданном среднем напряжении цикла. При увеличении среднего напряжения цикла σт предел выносливости σтах возрастает, а предельная амплитуда цикла σа уменьшается. Степень ее уменьшения зависит от чувствительности материала к асимметрии цикла, характеризуемой коэффициентом φσ. Таблица 4.6
Циклы, имеющие одинаковые коэффициенты асимметрии, называются подобными и обозначаются на диаграмме предельных напряжений точками, лежащими на одном луче, проведенном под соответствующим углом β. Это видно из формулы 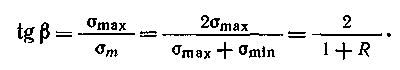 Экспериментально установлено, что отношение предельных амплитуд гладких образцов и образцов с концентрацией напряжений не зависит от среднего напряжения цикла. Согласно этому, коэффициенты концентрации напряжений принимаются одинаковыми для симметричных и асимметричных циклов, а продольная амплитуда напряжений для детали определяется по формуле 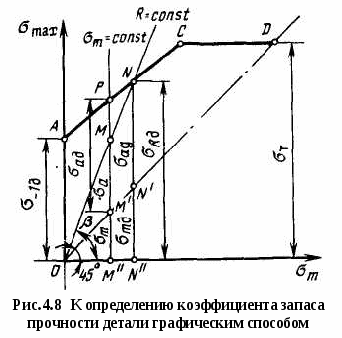 (28)М  аксимальное предельное напряжение асимметричных циклов или  Диаграмма предельных напряжений детали, показанная на рис. 4.8, используется для определения запасов прочности. Пусть напряжения (σmax, σa, σm) действуют на деталь в точке М. Если ожидаемые перегрузки соответствуют условию простого нагружения, т е. происходят при постоянной степени асимметрии (R = const), то предельное напряжение для рассматриваемого цикла будет в точке N и запас прочности 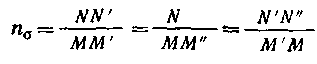  В результате совместного решения уравнений линий предельных напряжений АС и ON определяются ордината точки N и запас прочности при действии нормальных напряжений  (29)Аналогично при действии касательных напряжений 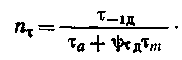 (30)Если при перегрузках среднее напряжение не изменяется (σm = const), а амплитуда растет, т. е. рабочие напряжения возрастают по прямой М"Р, то запас прочности  (31)Детали буровых машин обычно работают в условиях простого нагружения, и запас прочности следует рассчитывать по формулам (29) и (30). При совместном действии нормальных и касательных напряжений запас прочности определяется по формуле (24). Р 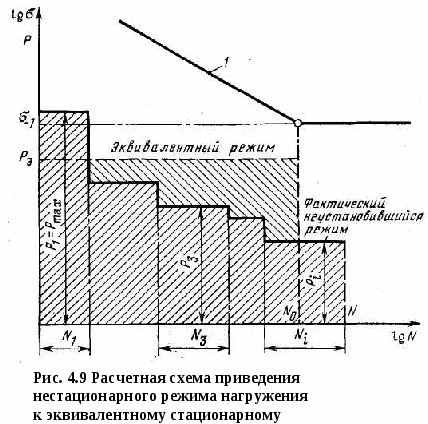 асчеты на выносливость при нестационарном нагружении базируются на следующих предположениях. Пусть нагрузки Р1, P2,..., Pi (или напряжения σ1, σ2, ….σi) действуют соответственно в течение N1….N3....Ni циклов нагружения (рис. 9). Отношение фактического числа циклов Ni действия некоторого напряжения σi - к числу циклов Nj при котором образец разрушается под действием того же напряжения σi называют цикловым отношением. Согласно гипотезе о суммировании усталостных повреждений, действие каждой группы нагрузок не зависит от порядка их чередования и одинаковые цикловые отношения различных по величине перегрузок вызывают одинаковую степень усталостного повреждения. В предположении линейного накопления усталостных повреждений  (32)где а — экспериментально устанавливаемый коэффициент, принимаемый (в запас) равным единице. При принятых обозначениях уравнение кривой выносливости 1 (рис. 9) имеет вид:  (33)где σR — предел выносливости при базовом числе циклов N0. На основе принятых предположений нестационарное нагружение заменяют некоторым эквивалентным стационарным нагружением, действие которого эквивалентно фактическому нестационарному нагружению. В практике применяются различные варианты приведения нестационарного нагружения к эквивалентным стационарным нагружениям. Любую из действующих нагрузок Pi (чаще Pmax) или вызываемое ею напряжение σi (σmax) принимают постоянной, действующей в течение соответствующего уровню нагружения так называемого эквивалентного числа циклов N3. Тогда, принимая, например, напряжение равным σmax, на основании формул (32) и (33) получим (а = 1)  откуда 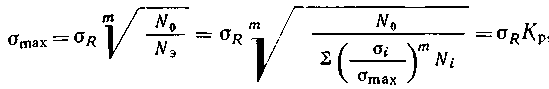 (34)и   (35)где — коэффициент режима нагрузки. Из формулы (35) следует, что при эквивалентном числе циклов Nэ В другом варианте приведения нестационарное нагружение заменяют режимом с постоянным эквивалентным уровнем нагружения Рэ (σэ), который действует в течение заданного срока службы, определяемого суммарным числом циклов ΣNi или числом N0, соответствующим точке перегиба кривой выносливости. Согласно этому  откуда выводится формула в следующем удобном для расчетов виде: 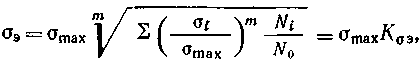 (36)или   (37)где — коэффициент эквивалентности. Для расчета коэффициента эквивалентности используются статистические данные о величине нагрузок, возникающих в детали в процессе эксплуатации, и количестве циклов их повторения в продолжение одного блока нагружения, соответствующего бурению одной типовой скважины. Практически значения коэффициентов эквивалентности изменяются в пределах 0,5 ≤ К0э ≤ 1. При расчете по касательным напряжениям значение коэффициента эквивалентности К0э определяются по формуле (36), в которой нормальные напряжения заменяются касательными, вызванными, передаваемыми крутящими моментами. Запасы прочности при нестационарном нагружении определяются по формулам: для симметричных циклов переменных напряжений  (38)для асимметричных циклов переменных напряжений  (39)Рекомендации по выбору расчетных нагрузок, минимально допустимых запасов прочности, коэффициентов асимметрии цикла и эквивалентности, разработанные Уралмашзаводом, приведены в табл. 2П приложения. Следует отметить, что величины коэффициентов эквивалентности зависят от проходки на долото, механической скорости бурения и других показателей, определяющих загрузку и оборачиваемость буровых машин и оборудования. При увеличении проходки на долото уменьшается загрузка подъемного механизма. На буровые насосы и ротор аналогично влияет повышение скоростей бурения. Это указывает на необходимость уточнения коэффициентов эквивалентности при существенных изменениях показателей бурения. Определение исходных данных для расчетов на выносливость элементов трансмиссий . При расчетах на выносливость используется закон линейного накопления повреждений при многократном воздействии на элементы трансмиссий амплитуд разных уровней. Определение исходных расчетных данных сводится к расчету эквивалентных нагрузок в виде произведения принимаемой в расчет основной нагрузки на коэффициент долговечности. Эквивалентная нагрузка - это такая нагрузка, действие которой по эффекту накопления повреждений эквивалентно действию реальной нагрузки. Методики для определения эквивалентных нагрузок элементов трансмиссий, базируются на следующих основных положениях. 1. Эксплуатационная нагруженность трансмиссий определяется средним значением   и коэффициентом вариации v крутящего момента, статистическое распределение амплитуд которого можно считать усеченным нормальным.2. В качестве средней нагрузки принимается крутящий момент в силовой цепи к органу, соответствующий реализации устойчивого момента My двигателей.3. Допустимой считается динамичность нагрузок для трансмиссии наиболее нагруженного органа, оцениваемая коэффициентом вариации v ≤ 0,6. При значениях v ≥ 0,6 следует принимать меры по его снижению, например, применять демпфирующие устройства и др. Численные значения коэффициентов вариации v можно определять по расчетным зависимостям, либо по результатам вычислительного эксперимента, либо по данным экспериментальных исследований машин-аналогов. Здесь  - максимальный длительно действующий момент;  - максимальная длительно действующая амплитуда крутящего момента; Рдл - максимальная длительно действующая нагрузка на подшипники, определяемая по Мдл.Значения коэффициентов долговечности определяются по зависимостям. 1. Для расчета зубьев колес на выносливость: контактную  изгибную для деталей с твердостью поверхности НВ > 350  изгибную для деталей с твердостью поверхности НВ < 350  2. Для расчета валов: на изгибную выносливость  на усталостную прочность при кручении  3. Для расчета долговечности шарико - и роликоподшипников:  Здесь 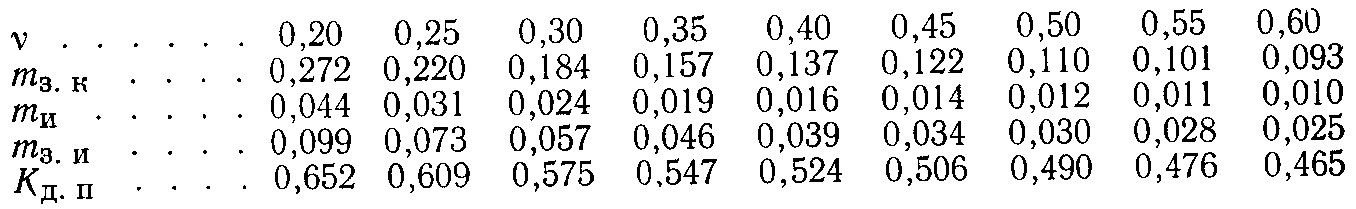 - расчетное число циклов нагружений элементов трансмиссии; п - частота вращения детали, об/мин; Тр — расчетное время работы детали, ч (обычно принимают 5000 ч); Nо - базовое число циклов нагружения, принимаемое в соответствии с рекомендациями (см. выше) - соответствующие коэффициенты эквивалентности, принимаемые в зависимости от v. При расчетах на выносливость зубьев колес по ГОСТ 21354—87, при определении расчетных напряжений в качестве нагрузки принимают Mдл, а при определении:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
;
.