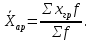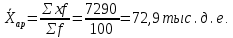Конспект лекций по дисциплине статистика

• Название: Конспект лекций по дисциплине статистика
• Дата: 01.02.2022
• Размер: 401.38 Kb.
• Имя файла: konspect.docx
• Тип: Конспект; #348809
• страница: 5 из 7

Относительная величина координации выражаются в виде коэффициентов. При исчислении относительных величин координации велико значение не только выбора базы сравнения, но и вообще выбора явлений, которые, могут быть сравнимы между собой.

Относительная величина сравнения показывает соотношение одноименных величин, относящихся к разной территории или к разным объектам, за один и тот же период времени и применяется для сопоставления экономических показателей. Они должны быть сопоставимы между собой

Относительная величина интенсивности( i_и) показывает степень распространенности данного явления в изучаемой среде и образуется в результате сравнения разноименных, но определенным образом связанных между собой абсолютных величин.

Относительные величины интенсивности, в отличии от других видов относительных величин, всегда выражаются именованными числами, например, плотность населения 8,6 чел./км². Разновидностью относительных величин интенсивности являются относительные показатели уровня экономического развития, характеризующие уровни ВВП, ВНП, национального дохода и др. показателей на душу населения и играющие важную роль в оценке развития экономики страны.

1.3 Средние величины и показатели вариации
Средняя величина – это обобщающая характеристика однородной совокупности явлений по определённому признаку.

В статистике используются различного вида средние величины: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, средняя хронологическая и т.д. Чтобы определить среднюю арифметическую простую, нужно сумму всех значений данного признака Σx разделить на число единиц n, обладающим этим признакам. Она применяется в тех случаях, когда имеются не сгруппированные индивидуальные значения признака.

Средняя арифметическая взвешенная есть частное от деления суммы произведений вариантов и соответствующих им частот Σxf на сумму всех частот Σ f. Частоты (f), фигурирующие в формуле средней, принято называть весами, вследствие чего средняя арифметическая, вычисленная с учетом весов, и получила название взвешенной.

В отдельных случаях веса могут быть представлены не абсолютными, а относительными величинами (в процентах или долях единицы). Тогда формула средней будет иметь вид

где d – частость, т.е. доля каждой частоты в общей сумме всех частот.

Если частоты подсчитывают в долях (коэффициентах), то Σ d = 1, формула средней арифметической взвешенной имеет вид:

.

Часто приходится исчислять среднюю по групповым средним или по средним отдельных частей совокупности (частным средним), т.е. среднюю из средних. Вычисление средней арифметической взвешенной из групповых среднихx_гр осуществляется по формуле


Если значения осредняемого признака заданы в виде интервалов («от – до»), т.е. интервальных рядов распределения, то при расчёте средней арифметической величины в качестве значения признаков в группах принимают середины этих интервалов, они рассчитываются как простая средняя между верхней и нижней границами каждого интервала. Если в ряду распределения есть открытые интервалы (первый и последний), их величина условно приравниваются к интервалам, примыкающим к ним. При таком исчислении средней допускается некоторая неточность, поскольку делается предположение о равномерности распределения признака внутри группы. Однако ошибка будет тем меньше, чем уже интервал и чем больше единиц в интервале.

Пример. Рассчитаем среднемесячную заработную плату рабочих по формуле средней арифметической взвешенной. После того, как найдены середины интервалов, варианты умножают на частоты (веса) и сумму произведений (тыс. д. е.) делят на сумму частот (весов). (табл. 4).



Т а б л и ц а 4 - Распределение рабочих по уровню ежемесячной оплаты труда.

Группы рабочих по оплате труда, тыс. д.е.	Число рабочих, чел.f	Середина интервала, тыс. д.е. x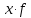
До 50	5	45	225
50 - 60	15	55	825
60 - 70	20	65	1300
70 - 80	30	75	2250
80- 90	16	85	1360
90 и более	14	95	1330
Итого	100	-	7290

Средняя арифметическая и ее свойства. Рассмотрим основные свойства средней арифметической.

Первое свойство. Нулевое свойство средней величины заключается в том, что сумма отклонений вариант от их средней арифметической величины равна нулю.



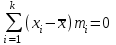
Второе свойство. Если все варианты уменьшить (или увеличить)на одно и то же постоянное число, то средняя арифметическая из этих вариант уменьшится (или увеличится) на то же самое число.

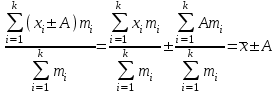
Пример. Пусть заработная плата каждого работника фирмы увеличилась за некоторый период на 15000 д.е. Тогда средняя заработная плата всех работников фирмы увеличилась также на 15000 д.е.

Третье свойство. Если все варианты одинаково увеличить (или уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (или уменьшится) во столько же раз.

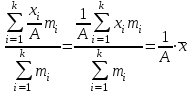
Пример. Так, если бы заработная плата каждого работника фирмы увеличилась на 10%, то и средняя заработная плата всех работников фирмы увеличилась бы на 10%.

Четвертое свойство. Если же все веса средней одинаково увеличить (или уменьшить) в несколько раз, средняя арифметическая не изменится. Увеличение всех весов в несколько раз приводит к тому, что во столько же одновременно увеличится и числитель, и знаменатель дроби (средней арифметической), поэтому значение дроби не изменяется.

Для упрощения расчётов средней идут по пути уменьшения значений вариантов и частот. Наибольшее упрощение достигается, когда в качестве А выбирается значение одного из центральных вариантов, обладающего наибольшей частотой, в качестве I – величина интервала. Величина А называется началом отсчёта, поэтому такой метод вычисления средней называется «способом отсчёта от условного нуля» или «способом моментов».

=

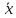
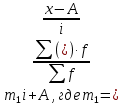
Средняя гармоническая. Средняя гармоническая применяется в тех случаях, когда частоты (веса) не приводятся непосредственно, а входят сомножителями в один из имеющихся показателей.

Пример. Автомобиль доставил товары в три магазина фирмы, которые удалены от головного предприятия на одинаковое расстояние. Так, до первого магазина, расположенного на шоссейной дороге, автомобиль прошел путь со скоростью 50 км/час, до второго, по проселочной дороге, — 40 км/час, а в третьем случае автомобилю пришлось полпути пройти через лесной массив, и скорость движения составила только 30 км/час.

Требуется определить среднюю скорость движения автомобиля.

На первый взгляд представляется, что средняя скорость движения может быть определена по формуле простой арифметической:
=
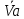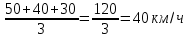
В подобных случаях нужно применить формулу средней гармонической простой (не взвешенной):



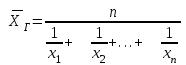
или в сокращенном виде



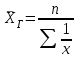
где X_Г— средняя гармоническая;
1 1 1 1

—; —; —... — — числа, обратные заданным вариантам.

х х₁ х₂ х_п

Простая гармоническая средняя есть отношение числа вариант к сумме обратных значений этих вариант.

Для нашего примера будем иметь:

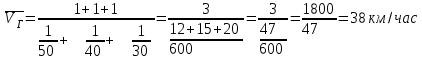
В нашем примере средняя арифметическая ( 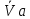) оказалась больше средней гармонической V_Г, при этом абсолютная ошибка завышения составляет 2 км/час(38 – 40), а относительная — 5%

( 2 ∙100 / 40)

Средняя геометрическая. Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, полученные как произведение цепных коэффициентов роста. Средняя геометрическая рассчитывается как корень степени n из произведений вариантов признака x:
= =
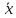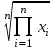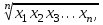
где n – число вариант; Π – знак произведения.
Средняя хронологическая— это средний уровень ряда динамики т.е. средняя, исчисленная по совокупности значений показателя в разные моменты или периоды времени. В зависимости от вида ряда динамики применяются различные способы ее расчета, а именно расчет: средней хронологической интервального ряда; средней хронологической моментного ряда.

Средней хронологической интервального ряда является средняя величина из уровней интервального ряда динамики и исчисляется по формуле:
=

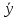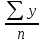
где 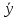— средний уровень ряда;

у — уровень ряда динамики;

п — число членов ряда.
Средней хронологической моментного ряда является средняя величина из уровней моментного ряда динамики.

При равных промежутках времени меж-
ду датами, на которые имеются данные, и равномерном изменении размера показателя между датами средняя хронологическая моментного ряда обычно исчисляется по формуле:



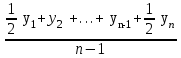
y =
n — число всех членов ряда;

у -— средний уровень.

Если периоды времени, отделяющие одну дату от другой, не равны между собой, то расчет средней хронологической моментного ряда производится по формуле средней взвешенной арифметической, в качестве весов которой принимаются отрезки времени между датами, т.е. по формуле:
=

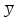
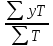где Т — время, в течение которого данный уровень ряда (у) оставался без изменения.

Например, По состоянию на 01.01.2012 года численность работников локомотивного депо составила 1220 человек. 5 января на работу было принято 2 человека, 16 января – уволено 3 человека, 29 января - принято 4 человека. Среднесписочная численность работников за январь месяц составит 1221 человек.



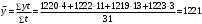
Структурные средние. Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Мода (М₀)– это есть варианта, у которой частота (вес) в ряду распределения наибольшая.

Вычисление моды для интервальных рядов с равными интервалами производится по формуле:

М₀ = х₀ + r_i ,

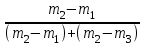где х_о – начало модального интервала; r_i – величина интервала;

m₂ – частота модального интервала;

m₁ – частота интервала, предшествующего модальному;

m₂ – частота интервала, следующего за модальным.

Медиана (М_е) – варианта, находящаяся в середине ранжированного (упорядоченного) ряда распределения. Для ее определения достаточно расположить в порядке возрастания или убывания все варианты. Серединная варианта и будет являться медианой. Медиана делит ряд на две равные части – со значениями признака меньше медианы и со значениями признака больше медианы. Если число значений в распределённом ряду чётное, то медиана равна средней из двух вариант, находящихся в середине ряда.

Расчет медианы интервального ряда производится по формуле:
М = х_Ме + r_i
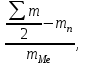
где х_Ме – начало (нижняя граница) медианного интервала;

r_i – величина интервала;

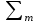- сумма накопленных частот ряда;

m_n – накопленная частота вариант, предшествующих медианному;

m_Me – частота медианного интервала.

Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет его асимметрию Если М₀ < М_е< , то имеет место правосторонняя асимметрия, при 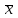< М_е< М₀ следует сделать вывод о левосторонней асимметрии ряда.

Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.

К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Размах вариации R – представляет собой разность между максимальным x_max и минимальным x_min значениями признака.


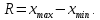
Среднее линейное отклонение:

для не сгруппированных значений



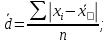
где n – число членов ряда;

для сгруппированных значений,



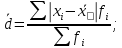
где Σf – сумма частот вариационного ряда.

Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий ( в зависимости от исходных данных):

простая дисперсия

для не сгруппированных значений

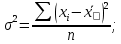
для сгруппированных значений

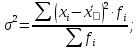
Расчёты по этим формулам можно упростить, если использовать свойства дисперсии. Первое – если все значения признака уменьшить или увеличить на одну и ту же величину А , то дисперсия от этого не измениться;

Второе – если все значения признака уменьшить или увеличить в одно и то же число раз ( i ) , то дисперсия соответственно уменьшится или увеличится в i² раз.

Используя второе свойство дисперсии, разделив все варианты на величину интервала, получим следующую формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:

,

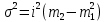где i - величина интервала;

момент второго порядка;



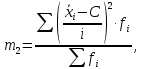
квадрат момента первого порядка.



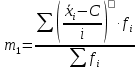
Среднее квадратическое отклонение:
для несгруппированных значений

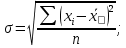
для сгруппированных значений

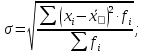
Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности; оно показывает на сколько в среднем отклоняются конкретные варианты от их среднего значения. Среднее квадратическое отклонение является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты.
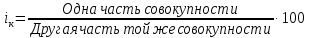
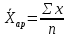
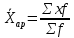
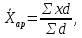
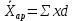