Конспект лекций по дисциплине статистика
 Скачать 401.38 Kb. Скачать 401.38 Kb.
|
|
Дисперсия альтернативного признака. Среди варьирующих признаков встречаются такие, вариация которых проявляется в том, что у одних единиц совокупности они встречаются , а у других нет. Обозначим: 1 – наличие интересующего нас признака; 0 – его отсутствие; p – доля единиц, обладающих данным признаком; q - доля единиц, не обладающих данным признаком; p + q = 1.Отсюда q = 1 – p. Исчислим среднее значение альтернативного признака и его дисперсию. среднее значение альтернативного признака 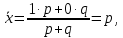 дисперсия альтернативного признака 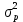 = =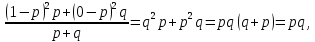 Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее совокупность и тем более типичной будет средняя величина. Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее совокупность и тем более типичной будет средняя величина. Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической: 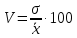 Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%. Правило сложения дисперсий. Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку. Тогда, наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучить вариацию для каждой из составляющих её групп, а также и между этими группами. Если совокупность расчленена на группы по одному фактору, изучение вариации осуществляется посредством исчисления и анализа трёх видов дисперсий: общей, межгрупповой и внутригрупповой. Общая дисперсия σ2 измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию для несгруппированных значений 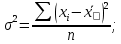 для сгруппированных значений 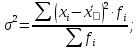 Межгрупповая дисперсия δ2 характеризует систематическую вариацию результативного порядка, обусловленную влиянием признака-фактора, положенного в основание - группировки. Она равна среднему квадрату отклонений групповых (частных) средних xiот общей средней. 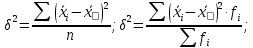 Внутригрупповая (частная) дисперсия σ i 2 отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтённых факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам: 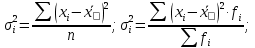 На величину частных, внутригрупповых дисперсий не влияет групповой признак. Поэтому, чтобы получить представление об общей вариации признака под влиянием случайных причин, следует рассчитать среднюю из внутригрупповых или частных дисперсий, которая будет равна: 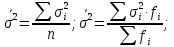 Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий: 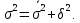 3. Выборочное наблюдение Наблюдение организуется таким образом, что эта часть отобранных единиц представляет всю совокупность. Вся изучаемая совокупность, из которой производится отбор некоторого числа единиц для выборочного наблюдения, называется генеральной совокупностью. Часть генеральной совокупности, подлежащая выборочному обследованию, называется выборочной совокупностью. Численность (объем) генеральной совокупности обозначим буквой N, а численность выборочной совокупности обозначим буквой n. При выборочном наблюдении обычно ставят две задачи: определение среднего размера изучаемого признака и определение доли изучаемого признака в данной совокупности. При статистических исследованиях (сплошных и выборочных) возникают ошибки двух видов: регистрации и репрезентативности. Ошибки регистрации могут иметь случайный (непреднамеренный) и систематический (тенденциозный) характер. Случайные ошибки обычно уравновешивают друг друга, поскольку не имеют преимущественного направления в сторону преувеличения или преуменьшения значения изучаемого показателя. Систематические ошибки направлены в одну сторону вследствие преднамеренного нарушения правил отбора. Их можно избежать при правильной организации и проведении наблюдения. Ошибки репрезентативности присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Они представляют собой расхождение между значениями показателей, полученных при выборке, и значениями показателей этих же величин, которые были бы получены при проведённом с одинаковой степенью точности сплошном наблюдении, т.е. между величинами выборочных и соответствующих генеральных показателей. Исчисленные обобщающие характеристики в генеральной совокупности называются генеральными: 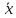 - генеральная средняя, а- генеральное среднее квадратическое отклонение, Р – генеральная доля, полученная как отношение числа М единиц, обладающих данным признаком, ко всей численности N генеральной совокупности, - генеральная средняя, а- генеральное среднее квадратическое отклонение, Р – генеральная доля, полученная как отношение числа М единиц, обладающих данным признаком, ко всей численности N генеральной совокупности, 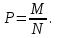 Исчисленные обобщающие характеристики в выборочной совокупности называются выборочными: 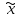 - выборочная средняя, - выборочная средняя, 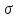 - выборочное среднее квадратическое отклонение, w – выборочная доля (частость) – отношение числа m единиц выборочной совокупности, обладающих данным признаком, ко всей численности n выборочной совокупности, т.е. - выборочное среднее квадратическое отклонение, w – выборочная доля (частость) – отношение числа m единиц выборочной совокупности, обладающих данным признаком, ко всей численности n выборочной совокупности, т.е.  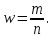 Пример. В табл. 5 приведены данные испытания крепости нити. Требуется определить среднее квадратическое отклонение крепости нити выборочной совокупности от ее генеральной. Таблица 5 - Данные испытания 100 одиночных нитей на крепость
К – число, кратное величине интервала. Средняя выборочная (средняя крепость нити выборочной совокупности) равна 183,6 грамма 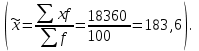 Среднее квадратическое отклонение равно 43,0 граммам: 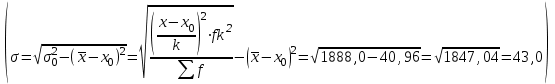 Поскольку проведение сплошного наблюдения заменяется выборочным, а исчисление средней генеральной заменяется исчислением средней выборочной, важно установить, насколько полученная средняя выборочная является характерной для данной генеральной совокупности и представляет ли она среднюю генеральную 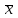 , т.е. , т.е.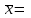 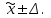 Чем меньше величина отклонения 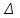 , тем точнее выборочная средняя воспроизводит генеральную среднюю. Величина этого отклонения и определяет степень точности выборочного наблюдения. , тем точнее выборочная средняя воспроизводит генеральную среднюю. Величина этого отклонения и определяет степень точности выборочного наблюдения.Ошибки выборочного наблюдения, которые иначе называют ошибками репрезентативности, возникают вследствие специфики самого метода и именно потому, что обследуется не вся совокупность, а лишь его часть, отобранная в случайном порядке. Определение средней величины этих ошибок и их возможных границ, а следовательно, определение достоверности данных выборочного наблюдения, является основной задачей теории выборочного исследования. Средняя величина ошибки 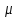 для выборочной совокупности, отобранной в случайном порядке для выборочной совокупности, отобранной в случайном порядке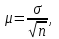 где 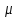 - средняя ошибка выборки; - средняя ошибка выборки;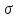 - среднее квадратическое отклонение; - среднее квадратическое отклонение;n – численность выборочной совокупности. Применяя эту формулу, получим следующую величину средней ошибки для нашего примера 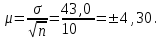 Величина средней ошибки выборки зависит, прежде всего, от показателей колеблемости значений признаков в выборочной совокупности. Степень колеблемости значений признаков определяется средним квадратическим отклонением 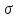 . Чем меньше величина среднего квадратического отклонения, тем меньше величина средней ошибки при той же численности выборки. . Чем меньше величина среднего квадратического отклонения, тем меньше величина средней ошибки при той же численности выборки. Величина средней ошибки зависит от численности выборки. Увеличивая или уменьшая объем выборки n, можно регулировать величину ошибки 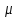 . Чем больше единиц будет охвачено выборочным наблюдением, тем меньше будет величина ошибки, так как тем точнее будет представлена генеральная совокупность. Полученная величина ошибки . Чем больше единиц будет охвачено выборочным наблюдением, тем меньше будет величина ошибки, так как тем точнее будет представлена генеральная совокупность. Полученная величина ошибки 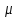 характеризует среднее отклонение средней выборочной от средней генеральной. характеризует среднее отклонение средней выборочной от средней генеральной. Величина пределов конкретной ошибки зависит от степени вероятности, с которой измеряется ошибка выборки. Ошибка выборки, исчисленная с заданной степенью вероятности, представляет предельную ошибку выборки. Если через 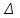 обозначим предельную ошибку, частное от деления обозначим предельную ошибку, частное от деления 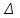 на на 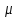 приравняем к t, тогда можно записать приравняем к t, тогда можно записать 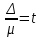 , отсюда , отсюда 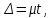 а так как а так как 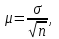 то то 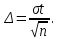 Величина предельной ошибки зависит от величины средней ошибки и коэффициента t. Коэффициент зависит от степени вероятности, с которой производится выборочное наблюдение. При вероятности 0,683 значении t равно 1. При вероятности 0,954 значении t равно 2. При вероятности 0,997 значении t равно 3. Величину вероятности для различных значений t можно определить на основе теоремы Лапласа. На практике пользуются готовыми таблицами значений этой функции, вычисленных для различных значений t. С увеличением значения t вероятность Р быстро приближается к единице, так что практически обычно ограничиваются значениями t, не превышающими 2-3 единицы. Уже при значении t, равном 3, вероятность очень близка к единице. Это означает, что если бы из одной и той же генеральной совокупности было произведено большое число случайных выборок одинаковой численности, то в среднем на 1000 выборок приходилось бы 997 таких, в которых отклонение выборочной средней от генеральной не превышало 3 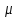 , и только в трех выборках отклонение могло бы выйти за эти пределы. , и только в трех выборках отклонение могло бы выйти за эти пределы.Указывая вероятные пределы случайной ошибки выборки, мы тем самым указываем и те пределы, за которые не выйдет характеристика генеральной совокупности. Определим для нашего примера, в каких границах должна заключаться средняя крепость нити в генеральной совокупности, с вероятностью 0,997. Средняя ошибка равна 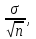 т.е. т.е. 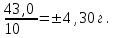 Предельная ошибка при заданной степени вероятности А равна 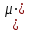 3, т.е. 3, т.е.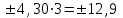 При проведении выборочного наблюдения часто возникает необходимость предварительного определения численности выборочной совокупности. Предположим, что мы хотим получить ошибку выборки вдвое меньшую, чем мы получили, т.е. ставим определенные условия: величина 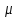 должна быть равна 2,15 вместо 4,30. Чтобы добиться уменьшения ошибки вдвое, нужно увеличить число наблюдений. Но на какое количество? Формула средней ошибки выборки позволяет ответить на этот вопрос: должна быть равна 2,15 вместо 4,30. Чтобы добиться уменьшения ошибки вдвое, нужно увеличить число наблюдений. Но на какое количество? Формула средней ошибки выборки позволяет ответить на этот вопрос: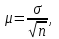 или или 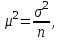 а отсюда а отсюда 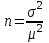 или или 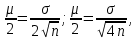 т.е. при сокращении ошибки вдвое численность выборки должна быть увеличена в четыре раза, при сокращении второе объем выборки должен быть увеличен в девять раз и т.д. Следовательно, чтобы получить среднюю ошибку выборки, для нашего примера равную 2,15, нужно подвергнуть наблюдению не 100, а 400 нитей. т.е. при сокращении ошибки вдвое численность выборки должна быть увеличена в четыре раза, при сокращении второе объем выборки должен быть увеличен в девять раз и т.д. Следовательно, чтобы получить среднюю ошибку выборки, для нашего примера равную 2,15, нужно подвергнуть наблюдению не 100, а 400 нитей.Для определения доли, изучаемого признака пользуются формулой средней ошибки выборки, которая имеет следующий вид: 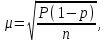 где Р – доля единиц, обладающих данным признаком в генеральной совокупности. Но этот показатель неизвестен, и его как раз нужно определить на основе выборочного наблюдения. Поэтому величина Р заменяется частостью 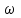 : :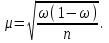 Допустим, что нужно установить для нашего примера долю нитей, имеющих крепость 190 граммов и больше. Частость (доля данного признака в выборочной совокупности) равна 0,56 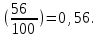 Отсюда средняя ошибка для доли: 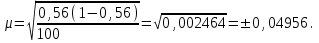 При заданной степени вероятности (0,997) предельная ошибка доли равна: 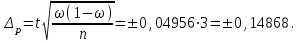 Пределы генеральной доли определяем по формуле: Р = 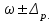 Отсюда Р = 0,56 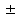 0,14868. 0,14868. Виды отбора единиц в выборочную совокупность По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности; при групповом отборе – качественно однородные группы или серии изучаемых единиц; комбинированный отбор предполагает сочетание первого и второго видов. |