Конспект лекций по дисциплине статистика
 Скачать 401.38 Kb. Скачать 401.38 Kb.
|
|
Случайный отбор. Единицы для наблюдения отбираются из всей совокупности. При этом каждая единица генеральной совокупности имеет равную возможность попасть в выборочную совокупность. По методу отбора различают повторную и бесповторную выборки. При повторной выборке общая численность единиц генеральной совокупности в процессе выборки остаётся неизменной. Ту или иную единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц вновь попасть в выборку. Такая выборка встречается редко. Чаще пользуются бесповторной выборкой. Бесповторным называется такой отбор, когда отобранная единица не возвращается обратно в генеральную совокупность. Следовательно, численность генеральной совокупности с каждой отобранной единице сокращается. Способом отбора определяется конкретный механизм или процедура выборки единиц из генеральной совокупности. По степени охвата единиц совокупности различают большие и малые (менее 30 наблюдений) выборки, наибольшее распространение получили следующие виды выборки: собственно-случайная, механическая, типическая, серийная, комбинированная. Собственно-случайный отбор представляет собой отбор единиц из всей генеральной совокупности посредством жеребьёвки или какого-либо иного подобного способа, например, с помощью таблицы случайных чисел. Механический отбор. При механическом отборе также применяется принцип случайного отбора. При этом из генеральной совокупности отбирается определенное число единиц через определенный интервал. При таком способе отбора генеральную совокупность механически разбивают на равные группы, число которых равно численности выборочной совокупности. Если при случайном отборе возникает лишь возможность попадания в выборку представителей всех тех состояний, которыми характеризуется изучаемый признак общей совокупности, то механический отбор направлен на то, чтобы действительно обеспечить попадание в выборку таких представителей. При механическом отборе средняя ошибка выборки определяется по тем же формулам, как и при повторном случайном отборе. Типический отбор используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп. Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом. Отбор единиц в типическую выборку может быть организован либо пропорционально объему типических групп, либо пропорционально внутригрупповой дифференциации признака. Отобранное по каждой группе количество единиц является частной выборочной совокупностью ni. Для каждой такой выборочной совокупности можно установить средний размер изучаемого признака 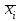 и среднее квадратическое отклонение и среднее квадратическое отклонение 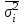 , которое характеризует внутригрупповую колеблемость признака в пределах своей группы. Этот показатель можно обобщить для всей совокупности в целом, т.е. найти показатель внутригрупповой колеблемости признака для всех групп совокупности, вместе взятых, , которое характеризует внутригрупповую колеблемость признака в пределах своей группы. Этот показатель можно обобщить для всей совокупности в целом, т.е. найти показатель внутригрупповой колеблемости признака для всех групп совокупности, вместе взятых, 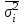 . .Чтобы получить общую выборочную среднюю для всех обследованных групп 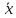 , надо из частных выборочных средних , надо из частных выборочных средних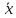 , вывести среднюю арифметическую взвешенную, причем в качестве весов можно взять или общую численность каждой группы, или численность выборки в каждой группе. Результат будет одинаковым, так как количество обследуемых единиц распределяется по группам пропорционально их удельному весу в общей совокупности. , вывести среднюю арифметическую взвешенную, причем в качестве весов можно взять или общую численность каждой группы, или численность выборки в каждой группе. Результат будет одинаковым, так как количество обследуемых единиц распределяется по группам пропорционально их удельному весу в общей совокупности. Ошибка выборки при типическом отборе определяется по той же формуле, что и при случайном отборе, однако вместо общей дисперсии признака 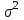 в этой формуле участвует средняя дисперсия из внутригрупповых в этой формуле участвует средняя дисперсия из внутригрупповых 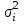 . .Чтобы получить общую выборочную среднюю для всех обследованных групп 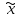 , вывести среднюю арифметическую взвешенную, причем в качестве весов можно взять или общую численность каждой группы, или численность выборки в каждой группе. Результат будет одинаковым, так как количество обследуемых единиц распределяется по группам пропорционально их удельному весу в общей совокупности. , вывести среднюю арифметическую взвешенную, причем в качестве весов можно взять или общую численность каждой группы, или численность выборки в каждой группе. Результат будет одинаковым, так как количество обследуемых единиц распределяется по группам пропорционально их удельному весу в общей совокупности. Серийная выборка. Иногда в практике выборочного наблюдения производят отбор целых групп единиц и внутри отобранных групп подвергают наблюдению все единицы без исключения. Для отбора серий применяют либо случайную выборку, либо механический отбор. Такая выборка называется серийной. Серийный отбор имеет большое практическое значение, так как легче организовать отбор и изучение нескольких серий единиц, чем сотен отдельных единиц. Но серийный отбор оказывается менее точным в смысле репрезентативности изучаемых показателей, чем другие способы отбора. Средняя ошибка серийной выборки исчисляется по формулам: При повторном отборе серий: для средней 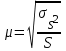 ; для доли ; для доли 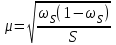 . .При бесповторном отборе серий: для средней 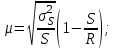 для доли для доли 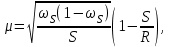 где 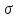 S2 – межсерийный квадрат отклонений; S2 – межсерийный квадрат отклонений;R - число серий в генеральной совокупности; S - число отобранных серий; 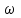 S- доля данного признака в среднем по всем обследованным сериям. S- доля данного признака в среднем по всем обследованным сериям.Необходимая численность выборки (n) определяется на основе формулы предельной ошибки выборки. Так, если выборка повторная, то n при собственно-случайном и механическом отборах определяется из формулы 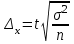 , ,где t – коэффициент доверия, вычисляемый по таблицам в зависимости от вероятности. Чтобы найти n, возведем обе части уравнения в квадрат и получим: 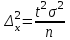 , откуда , откуда 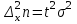 , а , а 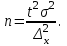 Объем выработки при исчислении доли определяется по этой же формуле, только вместо 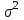 берется берется 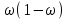 , т.е. , т.е. 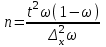 . .При бесповторном отборе численность выборки определяется из формулы 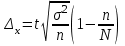 . .Возведя обе части уравнения в квадрат, получим: 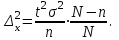 После преобразований имеем: 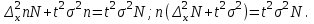 Отсюда 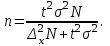 Аналогично исчисляется объем выборки и при определении доли, только вместо 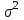 берется берется 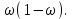 Пример. Объём генеральной совокупности составляет 2500 единиц. Требуется определить необходимый объем собственно-случайной выборки для повторного и бесповторного отборов для того, чтобы с вероятностью 0,954 предельная ошибка выборки при определении средней не превышало 20 единиц при среднем квадратическом отклонении 300 единиц. По условию задачи N=2500, t=2, 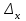 =20 и =20 и 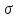 =300. =300.Для бесповторного отбора: 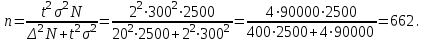 Таким образом, чтобы с вероятностью 0,954 получить предельную ошибку выборки не более 20 ед. при среднем квадратическом отклонении 300 ед., необходимо отобрать из 2500 ед. при повторном отборе 900, а при бесповторном – 662. Как видно, при прочих равных условиях объем выборки при бесповторном отборе меньше, чем при повторном. Так же исчисляется объем выборки и при определении доли. Определим по данным нашего примера, сколько нужно отобрать единиц для выборочного наблюдения, чтобы ошибка доли с вероятностью 0,954 не превышала 3% ( 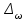 =0,03) при удельном весе рассматриваемых единиц в выборке, равном 80% ( =0,03) при удельном весе рассматриваемых единиц в выборке, равном 80% (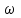 =0,8), N=2500. =0,8), N=2500.Для повторного отбора: 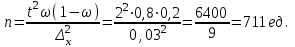 Для бесповторного отбора: 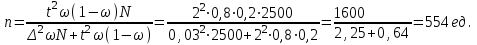 При определении необходимой численности выборки d2 и p(w) генеральной и выборочной совокупностей неизвестны, причем 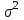 и w выборочной совокупности могут быть получены в результате проведения выборочного наблюдения. А без них нельзя установить необходимую численность выборки. В таких случаях фактическое значение дисперсии заменяют приближенным, полученным в результате проведения аналогичного выборочного наблюдения или пробного для ориентировочного суждения о ее размерах. Если признак альтернативный, то исходят из того, что ω = 0,5, а произведение и w выборочной совокупности могут быть получены в результате проведения выборочного наблюдения. А без них нельзя установить необходимую численность выборки. В таких случаях фактическое значение дисперсии заменяют приближенным, полученным в результате проведения аналогичного выборочного наблюдения или пробного для ориентировочного суждения о ее размерах. Если признак альтернативный, то исходят из того, что ω = 0,5, а произведение 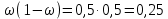 . Вообще, при определении выборочных данных для вычисления необходимой численности выборки исходят из максимально возможных значений. . Вообще, при определении выборочных данных для вычисления необходимой численности выборки исходят из максимально возможных значений. Рассмотрим другой пример выборки при исчислении выборочной доли для бесповторного отбора. Пример.Предполагается, что партия деталей содержит 8% бракованных. Необходимо определить нужный объем выборки, чтобы с вероятностью 0,954 можно установить долю брака с погрешностью не более 2%. Исследуемая партия 5 тыс. деталей. Объем выборки при исчислении выборочной доли для бесповторного отбора определяется по формуле: 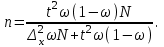 По условию задачи t=2, доля бракованных деталей 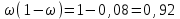 . Предельная ошибка доли по условию равна . Предельная ошибка доли по условию равна 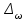 =0,02, а N=5000. =0,02, а N=5000.Подставляем эти данные в формулу: 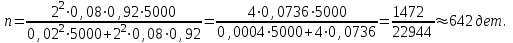 Чтобы с вероятностью 0,954 можно было утверждать, что предельная ошибка доли брака не превышает 2% необходимо из 5000 деталей отобрать 642. Распространение выборочных результатов на генеральную совокупность: способ прямого пересчета и способ коэффициентов. Способ прямого пересчета состоит в том, что средняя величина признака, найденная посредством выборки, умножается на число единиц генеральной совокупности. Например, необходимо определить средний процент брака в партии деталей, состоящей из 10000 деталей. Для выборочного наблюдения в случайном порядке было отобрано 900 деталей. Анализ качества отобранных деталей показал, что средний процент брака в данной совокупности составил 1,5%. Среднее квадратическое отклонение равно 0,3%. Максимальная ошибка выборочного наблюдения с вероятностью 0,997 равна 0,3%. Таким образом, средний процент брака в генеральной совокупности находится в пределах 1,5% 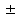 0,3%, т.е. колеблется от 1,2% до 1,8%. 0,3%, т.е. колеблется от 1,2% до 1,8%.Имея данные об общей величине партии, определяем общее количество бракованных деталей, которое будет колебаться в пределах 1,8-1,2% от 10000, или 180-120 единиц. Можно пределы не указывать, а пользоваться средней выборочной как генеральной средней. Тогда среднее количество бракованных банок в генеральной совокупности составит 1,5% от 10000, т.е. 150 единиц. Второй способ, или способ коэффициентов, применяется тогда, когда выборочное обследование проводится в целях проверки данных сплошного наблюдения. Сущность этого метода заключается в том, что на основании сопоставления данных сплошного и данных выборочного наблюдений устанавливают процент расхождений, который и служит коэффициентом поправки, налагаемой на данные сплошного наблюдения. |
