ТОК Лекции. Конспект лекций Самара Самарский государственный технический университет 2011

• Название: Конспект лекций Самара Самарский государственный технический университет 2011
• Анкор: ТОК Лекции.doc
• Дата: 29.03.2018
• Размер: 6.93 Mb.
• Имя файла: ТОК Лекции.doc
• Тип: Конспект; #17368
• страница: 13 из 18

Частотная манипуляция.

 При манипуляции видеоимпульсами (см. рис. 5.3, а) частота переносчика принимает только два значения (см. рис. 5.3, г). Спектр частот представлен на рис. 5.4, д.

Ширина полосы частот канала связи при передаче определяется допустимым временем установления сигнала на выходе входного фильтра приемника и девиацией частоты (частоты f₁ согласно рис. 5.3, г, на котором переходный процесс установления частоты не показан). Однако искажения, вносимые входным фильтром при ЧМ, несколько больше, чем при АМ. Поэтому для частотной манипуляции, считая, что ΔF/(2F_дев) =1,4, имеем:

ΔF_{ч min}=(1,7 ÷3)/τ. (5.13)

5. Реализация частотной модуляции.

Существуют прямые и косвенные методы реализации частотной модуляции. При прямых методах частотная модуляция осуществляется непосредственным изменением частоты задающего генератора. Наиболее распространенным косвенным методом является использование фазового модулятора для изменения фазы колебаний по закону частотной модуляции.

При прямых методах частота генератора изменяется путем изменения индуктивности катушки или емкости конденсатора, подключаемых параллельно катушке или конденсатору колебательного контура генератора. Прямые методы, несмотря на простоту, не могут обеспечить достаточной стабильности частоты генератора. Поэтому в модуляторах, основанных на этом принципе, в случае необходимости дополнительно применяют автоматическую подстройку частоты. В телемеханике, как правило, используют прямые методы частотной модуляции.

Демодуляция частотно-модулированных колебаний. Для этой цели частотно-модулированные колебания превращают сначала в колебания, модулированные по фазе или по амплитуде, из которых затем выделяется передаваемое сообщение. Поэтому различают частотно-амплитудные или частотно-фазовые (либо просто фазовые) детекторы. В телемеханике в большинстве случаев применяют частотно-амплитудные детекторы.

Простейший частотно-амплитудный детектор состоит из обычного колебательного контура (расстроенного относительно основной частоты приходящего сигнала) и амплитудного детектора. При изменении частоты сигнала значение напряжения на контуре изменяется. Однако из-за криволинейности ветвей резонансной кривой колебательного контура такие детекторы дают значительные нелинейные искажения.

Более совершенным частотно-амплитудным детектором является частотный дискриминатор, выполняемый с двумя вторичными расстроенными контурами (рис. 5.5, а).

Если, например, модулированные по частоте колебания, подаваемые на вход, лежат в полосе 1100 ÷ 1000 Гц, то контур К₁настраивается на частоту 1050 Гц, контур К₂ – на частоту 1100 Гц и контур К₃ – на частоту 1000 Гц (рис. 5.5, б).

Контур К₁является широкополосным, пропускающим частоты, на которые настраиваются контуры К₂ и К₃. Напряжения, снимаемые с контуров К₂, К₃, детектируются, и с резисторов R₁, R₂снимается напряжение, зависящее от частоты сигнала.

Когда на вход подается частота 1100 Гц, с резистора R₁ можно снять напряжение U₂, которое больше напряжения U₃ (на резисторе R₂) при прохождении частоты, например, 1070 Гц.

Диоды Д₁и Д₂включены таким образом, что напряжение U_вых на выходе дискриминатора равно разности напряжений: U_вых =U₂ – U₃. Поэтому резонансную кривую контура К₃можно изобразить в другой полярности (пунктир на рис. 5.11, б)по отношению к кривой контура К₂.

Если сложить резонансные кривые контуров К₂и К₃, то получится результирующая кривая дискриминатора, представляющая собой зависимость напряжения на выходе от частоты входного сигнала (рис. 5.11, в). На значительном участке эта характеристика линейна.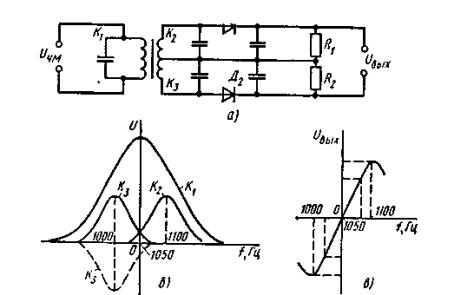



Рис. 5.5. Демодуляция частотно-модулированного сигнала:

схема частотного дискриминатора (а) и его характеристики (б, в)

 

Сравнение амплитудной (АМ) и частотной (ЧМ) модуляций показывает, что:

1) техническая реализация АМ проще, чем ЧМ;

2) полоса частот при АМ значительно меньше, чем при ЧМ;

3) помехоустойчивость ЧМ значительно выше АМ. Это объясняется тем, что помехи воздействуют в первую очередь на амплитуду сигнала (см. рис. 5.1, e),что при ЧМ не имеет существенного значения, так как в ЧМ-приемниках обычно применяют двустороннее ограничение сигнала (см. пунктир на рис. 5.1, е). В то же время при АМ изменение амплитуды сообщения вызывает изменение амплитуды переносчика, и такое ограничение, срезающее помехи, применять нельзя;

4) при ограниченной пиковой мощности передатчика средняя мощность АМ-сигнала оказывается меньше мощности ЧМ-сигнала. Это следует из рис. 5.1, ж,на котором изображена немодулированная несущая с максимальной амплитудой. При ЧМ амплитуда несущей не изменяется, а при АМ ее необходимо уменьшать до значения А (пунктир), что снижает среднюю мощность сигнала.

Из-за меньшей помехоустойчивости АМ как самостоятельный вид модуляции в телемеханике находит ограниченное применение и используется в основном как промежуточный вид модуляции при двойных модуляциях, о которых будет сказано далее. Большое применение нашла амплитудная демодуляция как промежуточный этап при частотной или фазовой демодуляции.

5.4. ДВУКРАТНАЯ НЕПРЕРЫВНАЯ МОДУЛЯЦИЯ

Для повышения помехоустойчивости передачи применяется двукратная модуляция. Например, амплитудно-модулированное сообщение дополнительно модулируют по частоте. Возникает двойная модуляция АМ-ЧМ. Из рис. 5.6 следует, что сначала сообщением модулируется по амплитуде первый переносчик, который называется поднесущей (рис. 5.6, б). Для наглядности частота переносчика взята соизмеримой с частотой сообщения.

Далее амплитудно-модулированный сигнал (рис. 5.6, в) как сообщение модулирует второй переносчик, или несущую (рис. 5.6, г), в результате чего возникает сигнал, модулированный по частоте (рис. 5.6, д).Иногда применяют модуляцию ЧМ-АМ, при которой помехоустойчивость обеспечивается ЧМ, а экономия полосы частот – АМ.

При этом первая поднесущая (рис. 5.6, б) модулируется сообщением (рис. 5.6, а) по частоте (рис. 5.6, е), а затем частотно-модулированный сигнал модулирует новую несущую (второй переносчик) по амплитуде (рис. 5.6, ж). На рис. 5.6, ж пунктирная огибающая повторяет частотно-модулированный сигнал, изображенный на рис 5.6, е. По такому же принципу образуется и двойная модуляция ЧМ-ЧМ.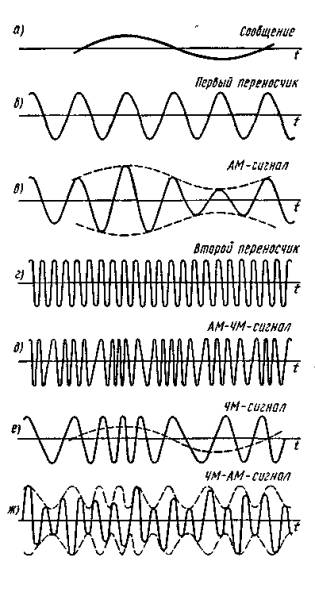


Рис. 5.6. Методы двукратных непрерывных модуляций.

а – передаваемое сообщение, б – первый переносчик (поднесущая), в – АМ-сигнал,
г – второй переносчик (несущая), д – АМ-ЧМ-сигнал, е – ЧМ-сигнал,

ж – ЧМ-АМ-сигнал

5.5. ИМПУЛЬСНЫЕ МЕТОДЫ МОДУЛЯЦИИ

Дословно «импульс» в переводе с латинского означает «толчок». Под импульсом понимают кратковременное воздействие электрического тока или напряжения на схему или устройство.

Последовательность импульсов характеризуется рядом параметров: амплитудой, длительностью, положением во времени, числом импульсов и т.д.

Используя последовательность импульсов в качестве переносчика, каждый из этих параметров можно изменять под воздействием сообщения, тем самым осуществляя так называемую импульсную модуляцию. Так как такой переносчик имеет много параметров, то и число импульсных методов модуляции достаточно велико. Это означает, что последовательность импульсов, будучи использованной в качестве переносчика, позволяет образовывать множество различных дискретных сигналов для передачи непрерывных сообщений. 

5.5.1. Амплитудно-импульсная модуляция

Амплитудно-импульсная модуляция (АИМ) – это изменение амплитуды импульсной последовательности пропорционально мгновенному значению сообщения.

На рис. 5.7, а представлено передаваемое сообщение, а на рис. 5.7, б – его переносчик – последовательность прямоугольных импульсов. Под воздействием мгновенных значений сообщения (тока или напряжения) амплитуда импульсов переносчика изменяется, как показано на рис. 5.7, в. Можно записать:

U_M =U(1 + m_AsinΩt), (5.14)

где U_M – амплитуда модулированных импульсов; U – амплитуда немодулированных импульсов; m_A – глубина модуляции при АИМ; Ω – угловая частота сообщения.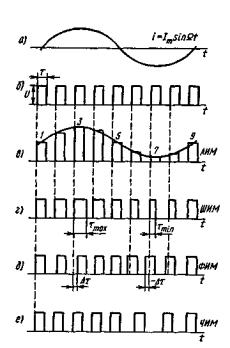



Рис. 5.7. Методы импульсной модуляции:

а – передаваемое сообщение; б – переносчик сообщения;
в – аплитудно-импульсная модуляция (АИМ); г – широтно-импульсная модуляция (ШИМ);

д – фазоимпульсная модуляция (ФИМ); е – частотно-импульсная модуляция (ЧИМ)
 Из-за плохой помехоустойчивости и погрешностей, возникающих при изменении коэффициента передачи линий связи, АИМ применяется в ТИ только как промежуточный вид модуляции, например, в системе АИМ-ЧМ.

5.5.2. Широтно-импульсная модуляция

Широтно-импульсная модуляция (ШИМ) – это изменение длительности импульсов пропорционально мгновенному значению сообщения.

На рис. 5.7, г показано, что под действием мгновенных значений сообщения изменяется длительность или ширина импульсов переносчика, расширяясь при увеличении мгновенного значения сообщения и суживаясь при его уменьшении (за счет положения заднего фронта импульса). Частота и амплитуда импульсов при ШИМ не изменяются. Помехоустойчивость ШИМ значительно выше помехоустойчивости АИМ, поэтому ШИМ нашла широкое применение. При ШИМ необходимо выбирать полосу частот по наиболее короткому импульсу ΔF=1/τ_min. Спектр частот ШИМ аналогичен спектру АИМ с той лишь разницей, что при ШИМ вокруг каждой гармоники имеется не две (как на рис. 5.2), а несколько пар боковых частот.

Используются и другие разновидности ШИМ, когда изменяется положение переднего фронта импульсов при неизменном положении заднего фронта или изменяются положения обоих фронтов.

5.5.3. Фазоимпульсная модуляция

Фазоимпульсная модуляция (ФИМ) – это изменение фазы импульсной последовательности пропорционально мгновенному значению сообщения.

ШИМ и ФИМ объединяются общим понятием времяимпульсной модуляции (ВИМ). На рис. 5.7, д показано, как изменяется положение импульса в зависимости от мгновенного сообщения: импульс сдвигается вправо на Δt при увеличении мгновенного значения и влево на -Δt при его уменьшении. При синусоидальной форме сообщения сдвиг, или девиация, импульса

Δt =Δt_maxsinΩt.

Полоса частот при ВИМ определяется длительностью импульса, которая в процессе модуляции не изменяется.

5.5.4. Частотно-импульсная модуляция (ЧИМ)

Из рис. 5.7, е следует, что при увеличении мгновенного значения сообщения частота импульсов возрастает, а при уменьшении – снижается. Таким образом, осуществляется модуляция по частоте импульсов, при которой длительность импульсов остается постоянной, изменяется лишь интервал между ними. Ширина полосы частот определяется длительностью импульса.

5.5.5. Кодоимпульсная модуляция (КИМ)

При кодоимпульсной модуляции сообщение квантуется по уровню и по времени, а затем каждый дискретный уровень передается с помощью кода в дискретные моменты времени. Если, например, квантованная ступенчатая функция λ`(t) передается обычным двоичным кодом, то ступенька, соответствующая уровню 1,передается комбинацией 0001 в момент времени t₀, вторая ступенька, соответствующая уровню 2, – комбинацией 0010 в момент времени t₁.Уровень 3 передается комбинацией 0100 и т.д.

Как и в других импульсных модуляциях, полоса частот в КИМ определяется длительностью импульса.

Кодоимпульсная модуляция нашла широкое применение в телемеханике.

5.5.6. Дельта-модуляция

Дельта-модуляция (Δ-модуляция) представляет собой передачу положительного или отрицательного импульса, соответствующего знаку приращения ступенчатой дифференциально квантованной функции [10].

По сравнению с известным обычным квантованием (например, при кодоимпульсной модуляции) дифференциальное квантование непрерывного сообщения имеет следующие особенности:

1. Дифференциально квантованная функция имеет приращение в дискретный момент времени только на один уровень.

2. Приращение дифференциально квантованной функции равно +1, если в момент квантования величина непрерывного сообщения больше величины дифференциально квантованной функции в предыдущий момент квантования, и приращение равно -1, если в момент квантования величина непрерывного сообщения меньше величины дифференциально квантованной функции.

Таким образом, при любом числе уровней квантования осуществляется передача лишь одного из двух дискретных сигналов, которыми передается только знак приращения функции. Из этого следует существенное преимущество Δ-модуляции – возможность получения большего быстродействия передачи, что особенно важно в телеизмерениях. Действительно, при КИМ каждое значение измеряемой величины передается многоразрядным кодом, а при Δ-модуляции – лишь одним импульсом, т.е. скорость передачи увеличивается в п раз, где п – число разрядов кода.

Δ-модуляция имеет следующие недостатки.

1. Ошибка на приёмной стороне может появляться из-за искажения кодового импульса.

2. Использование дифференциального квантования может приводить к появлению ошибки, вызванной отставанием ступенчатой функции от непрерывного сообщения при быстрых изменениях последнего из-за того, что переход ступенчатой функции через соседний уровень запрещён.

Обе эти ошибки могут накапливаться с течением времени, и несмотря на правильность последующей передачи эта ошибка будет существоватьдо тех пор, пока она не будет скомпенсирована ошибкой противоположного знака.

5.5.7. Разностно-дискретная модуляция (РДМ)

Разностно-дискретная модуляция представляет собой передачу положительного или отрицательного импульса, соответствующего знаку приращения квантованной функции, а также отсутствие сигнала при постоянстве квантованной функции [10]. При РДМ используется обычное квантование. Временные диаграммы процедуры РДМ показаны на рис. 5.8.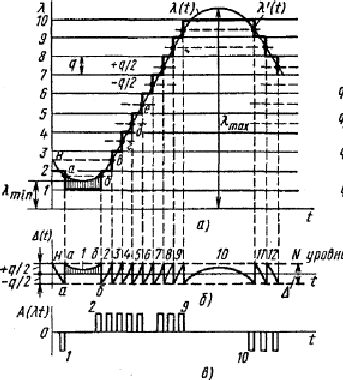


Рис. 5.8. Квантование сообщения по уровню:

а – квантование с постоянным шагом; б – погрешности квантования;

в – сигналы при разностно-дискретной модуляции
При переходе на более высокий уровень передается сигнал о единичном скачке вверх, а при переходе на более низкий уровень – сигнал о скачке вниз. Если сообщение не изменяет значения, сигнал отсутствует; на рисункепоказано, что между импульсами 1 и 2,а также 9 и 10 сигнала нет.

Разница между Δ-модуляцией и РДМ заключается в следующем.

1. При РДМ используется обычное квантование по уровню, а при Δ-модуляции – более сложное дифференциальное квантование.

2. Если при Δ-модуляции сигналы передаются периодически через равные промежутки времени Δt, то при РДМ – только в моменты изменения сообщения при переходе с одного дискретного уровня на другой. Таким образом, при медленно изменяющихся сообщениях РДМ-сигналы будут передаваться редко в отличие от Δ-модуляции, где они должны следовать через шаг квантования Δt. Преимущество РДМ состоит также в том, что ее применение для многоканальной системы телеизмерения позволяет увеличить быстродействие всей системы по сравнению, например, с такой же многоканальной кодоимпульсной системой. Это объясняется тем, что передача показаний каждого телеизмерения осуществляется не кодовой комбинацией, а одним импульсом, на что тратится меньше времени.

Недостатком РДМ является возможность появления и накопления ошибки в результате искажения кодового импульса. Этот недостаток настолько существен, что РДМ приходится применять в комбинации с КИМ.

5.5.8. Лямбда-дельта-модуляция

Этот вид модуляции вначале был предложен как λ-Δ-преобразование. Сначала непрерывная функция λ(t) квантуется по уровню и по времени [10]. Возможный результат такого квантования представлен на рис. 5.9, а.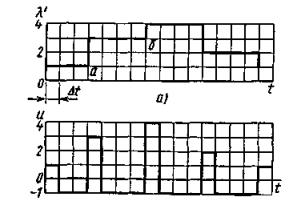



Рис. 5.9. Временные диаграммы λ-Δ-модуляции:

а – функция сообщения после квантования по уровню и по времени;
б – передача квантованной функции методом λ-Δ-модуляции
Квантованная ступенчатая функция передается таким образом: значение функции λ'(t)в первом интервале передается положительным импульсом с уровнем 1 в течение времени Δt (рис. 5.10, б). Сообщение о том, что до точки а квантованная функция не изменяется (рис. 5.10, а), передается дополнительным импульсом с отрицательным уровнем «-1». Переход функции на уровень 3 (в точке а) передается импульсом, амплитуда которого равна уровню 3.

Отсутствие изменения функции до точки б вновь передается уровнем «-1». Таким образом, передача осуществляется только в моменты изменения состояния функции. Такая передача особенно эффективна в случае, если сообщения мало изменяются во времени.

Использование уровня «-1» применяется для контроля исправности линии связи. Если эта процедура не применяется, то линия связи оказывается большую часть времени свободной и её можно использовать для передачи другой информации. В отличие от Δ-модуляции здесь передается не приращение функции, а полное значение, что устраняет возможность накопления ошибки.

5.5.9. Многократные методы модуляции

Сообщение может быть передано сложным сигналом, образованным несколькими поочередными модуляциями. Обычно такой сигнал является результатом двукратной модуляции: 1) импульсной, которой модулируется последовательность импульсов, или импульсная поднесущая (первый переносчик); 2) непрерывной, которой модулируется несущая (второй переносчик).

При трехкратных модуляциях первая модуляция импульсная, вторая и третья – непрерывные. Иногда применяют двойную модуляцию импульсной поднесущей: сначала осуществляют АИМ, которая затем преобразуется в ВИМ или ШИМ, а затем производят непрерывную модуляцию несущей. В результате возникает модуляция АИМ-ВИМ-АМ, АИМ-ШИМ-ЧМ и т.п.

На рис. 5.10 представлены различные варианты двукратных методов модуляции.

Промодулированная по амплитуде последовательность импульсов далее модулируется высокочастотной несущей, в результате возникает сигнал в виде радиоимпульсов АИМ-АМ, рис. 5.10, а. При ШИМ-АМ (см. рис. 5.10, б) импульсы ШИМ заполняются высокой частотой, в результате чего возникают радиоимпульсы одинаковой амплитуды и частоты, но разной длительности.

Если вторичная модуляция частотная, то амплитуда сигналов одинакова, но частота заполнения разная. Так, при АИМ-ЧМ импульсу 1 на рис. 5.7, в соответствует радиоимпульс частоты f₁ на рис. 5.17, в, а импульсу большей амплитуды (3 на рис. 5.7, в) – радиоимпульс большей частоты (f₂ на рис. 5.10, в). Импульс наименьшей амплитуды (7 на рис. 5.7, в) наполняется самой низкой частотой f₃. Интервалы времени между импульсами заполняются одной и той же частотой f₀, которая является немодулированной несущей. Двукратная модуляция ШИМ-ЧМ отличается от ШИМ-АМ лишь тем, что интервалы между импульсами заполняются частотой несущей (рис. 5.10, г).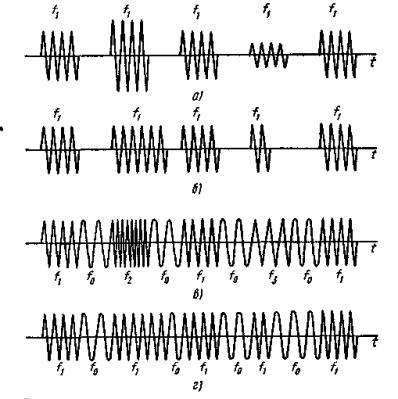


Рис. 5.10. Двукратные методы модуляции:

а – АИМ-АМ; б – ШИМ-АМ; в – АИМ-ЧМ; г – ШИМ-ЧМ
По указанному принципу может быть получен любой другой вариант двукратных модуляций. Правило их построения: сначала сообщение модулирует импульсную поднесущую (последовательность видеоимпульсов), которая, превращаясь в сигнал, модулирует высокочастотную несущую.

5.6. СПЕКТРЫ ИМПУЛЬСНЫХ СИГНАЛОВ

Современные системы телемеханики используют кодоимпульсный метод модуляции и передачу последовательным кодом.

Рассмотрим спектр частот периодической последовательности видеоимпульсов. Такой последовательностью можно моделировать передачу сигналов кодоимпульсной модуляции.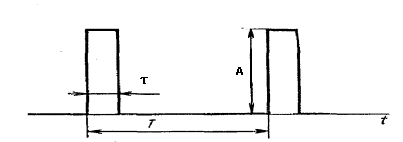



Рис. 5.11. Периодическая последовательность импульсов
Величина i = T/τ представляет собой величину, обратную скважности.

Бесконечная последовательность импульсов является периодической функцией времени F(t), и ее разложение производится помощью ряда Фурье: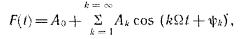

^(5.15)

где А₀ – постоянная составляющая; А_k – амплитуда k-той гармоники;
k – номер гармоники; k=1, 2, 3, ...; Ω=2π/Т – угловая частота; ψ_k –начальная фаза k-той гармоники;

Для последовательности прямоугольных импульсов  имеем: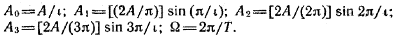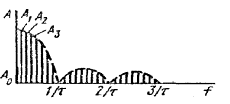




Рис. 5.12. Линейчатый спектр бесконечной последовательности импульсов:

f=Ω/2π
Анализ линейчатого спектра показывает, что воспроизведение формы видеоимпульса зависит только от полосы частот F, которая определяется длительностью видеоимпульса :

ΔF_ВИ = µ/τ, (5.16)

где µ – коэффициент воспроизведения формы импульса, его величина составляет 1 ≤ µ ≤ 2.

µ = 1 – нижняя граница (по линейчатому спектру).

µ ≤ 2 – практическое ограничение для лучшего использования полосы пропускания линии связи.

Передача импульсов в полосе частот ΔF=(1÷2)/τ вполне удовлетворительна, так как в телемеханике большинство устройств являются пороговыми, чувствительными к амплитуде импульса и нечувствительными к его форме.

Иногда в целях экономии полосы частот, а также в случаях, когда воспроизводимая форма импульса не играет особой роли, принимают μ=1/2. При такой сокращенной полосе частот F_min=0,5/τ предельная скорость передачи определяется следующим образом.

Так как  B=1/τ [Бод]  и  F_min=1/2τ, 

B_max=2F_min. _(5.17)

Передачу сигналов разностно-дискретной модуляции и лямбда-дельта-модуляции можно моделировать непериодической последовательностью. Непрерывный cпектр частот непериодической последовательности определяется выражением

^{. (5.18)}

Подставляя в это выражение подынтегральную функцию в виде прямоугольного видеоимпульса, получим непрерывный спектр, графическое отображение которого представлено на рис. 5.13.

Он напоминает график, показанный на рис. 5.12, отличаясь типом спектра. Из него видно, что и в этом случае

ΔF_ВИ = µ/τ , (5.19)

где µ – коэффициент воспроизведения формы импульса, его величина составляет 1 ≤ µ ≤ 2.

Подстановка в (5.18) в качестве подынтегральной функции в виде прямоугольного радиоимпульса даёт также непрерывный спектр, графическое отображение которого представлено на рис. 5.14.

Из него видно, что спектр частот радиоимпульса симметричен относительно несущей частоты f₁, основные соотношения его формы совпадают с соотношениями спектра частот видеоимпульса.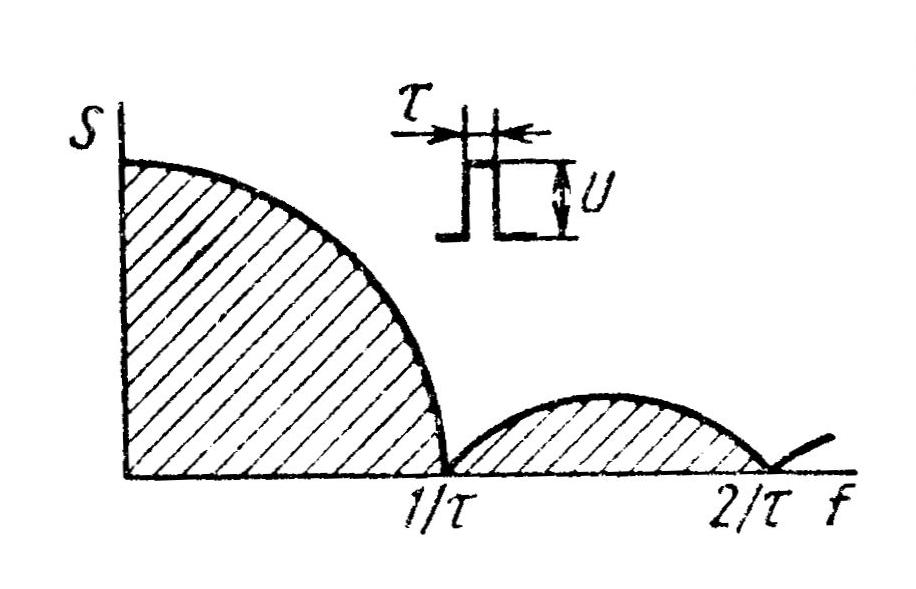



Рис. 5.13. Непрерывный cпектр частот видеоимпульса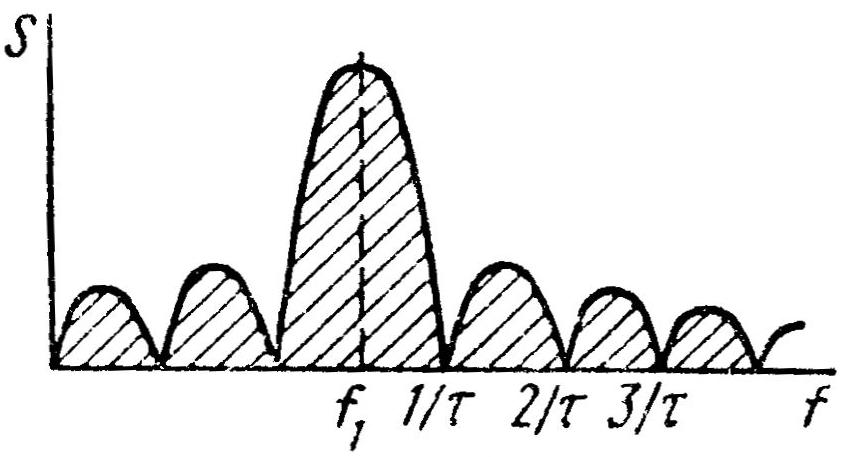



Рис. 5.14. Непрерывный спектр частот радиоимпульса:

f1 – частота несущей, τ – длительность радиоимпульса
По графику рис. 5.14 очевидно, что полоса пропускания, необходимая для передачи радиоимпульса,

ΔF_ри =2µ/τ, (5.20)

где µ – коэффициент воспроизведения формы импульса, его величина составляет 1 ≤ µ ≤ 2.

Сравнение формул (5.16), (5.19) и (5.20) показывает, что полоса пропускания частот линии связи при передаче импульсного сигнала определяется длительностью передаваемого импульса.
Пример 5.2

Сравним полосы частот, необходимые для передачи телемеханических сообщений методами временного разделения (ВР) и частотного разделения (ЧР) сигналов. Передача ведётся радиоимпульсами.

Будем считать, что быстродействие систем телемеханики, использующих частотное и временное разделение сигналов, одинаково. Быстродействие определим как передачу за определенный промежуток времени одного и того же числа сигналов.

Например, сигналы В₁-B₃ при временном и Ч₁-Ч₃ при частотном разделении передаются за время одного цикла Tц (см. рис. 3.3). Это значит, что при передаче трёх сигналов длительность импульса при ВР должна быть в три раза меньше длительности импульса при ЧР, так как команды при ЧР могут быть посланы одновременно, а при ВР – только последовательно во времени.

При равенстве быстродействий за цикл быстродействие в передаче одного сообщения при ВР будет выше, чем при ЧР.

В общем случае при передаче N сигналов команды при ВР в N раз короче, чем при ЧР, полоса частот, отводимая на каждую команду при ВР, в N раз шире, чем при ЧР.

Пусть Tц=3 мс, следовательно, t₁ = t₂ = t₃ = t = 1 мс. При временном разделении требуемая полоса частот для передачи радиоимпульса определяется по формуле (5.20) и поэтому F_ВР=2/t=2000 Гц.

При ЧР каждая команда передается в течение 3 мс и аналогичные расчёты дают требуемую полосу F_ЧР=660 Гц.

Если же за время Тц=3 мс передавать при ВР только одну команду, то она также займет полосу F_В1 660 Гц.

Таким образом, при одинаковом быстродействии требуются примерно одинаковые полосы частот при временном и при частотном разделении сигналов. Чем больше быстродействие системы, тем больше должна быть полоса частот независимо от способа разделения сигналов.

В общем случае при передаче N сигналов полоса частот при ВР в N раз короче, чем при ЧР, а полоса частот, отводимая на каждую команду при ВР, в N раз шире, чем при ЧР.

Полоса частот для передачи сообщений по N каналам при ВР с учетом добавления одного канала на синхронизацию составит ΔF_Σв=(N+1)ΔF_в1, где ΔF_в1 – полоса частот для передачи одного сообщения за время цикла.

При ЧР с учетом добавления защитных полос частот между командами требуемая полоса частот ΔF_Σч=1,2NF_ч1, где F_ч1 – полоса частот для передачи одного сообщения ЧР.

Условие равенства быстродействий в передаче одного сообщения F_В1=F_Ч1 имеет вид  ΔF_Σв/ΔF_Σч=(N+1)/(1,2N).

Практически в промышленных системах телемеханики для повышения достоверности передачи за один за цикл предаётся одно командное сообщение и быстродействие не играет решающей роли. Поэтому ВР дает некоторый выигрыш в полосе частот, так как сужению полосы частот при ЧР препятствуют технические трудности, связанные с выполнением узкополосных фильтров.

КЛЮЧЕВЫЕ ТЕРМИНЫ И ПОНЯТИЯ