Конспект лекций. Конспект лекций, задачи и упражнения

• Название: Конспект лекций, задачи и упражнения
• Анкор: Конспект лекций.docx
• Дата: 03.05.2018
• Размер: 0.51 Mb.
• Имя файла: Конспект лекций.docx
• Тип: Конспект; #18833
• страница: 2 из 10

1.2. Термохимия, закон Г.И. Гесса

 

Пример 1. При сгорании 6,048 г водорода в кислороде при 298,15 К в стандартных условиях выделяется 857,5 кДж теплоты. Определить стандартную энтальпию образования H₂O (ж) при 298,15 К.

 

Решение. Водород сгорает в кислороде согласно уравнению:

H₂ (ж) + O₂ (ж) = H₂O (ж)

Все вещества находятся в стандартных состояниях, поэтому энтальпия сгорания 1 моль Н₂ (2,016 г) и будет стандартной энтальпией образования Н₂О (ж) при 298,15 К; найдем эту величину:

6,048 – 857,5

2,016 – х, откуда х = 258,8;

H_oбp.H₂O(ж) = – 285,8 кДж/мoль.

 

Пример 2. Энтальпия какого процесса отвечает термину “стандартная энтальпия образования НNO₃ при 298,15 К”:

а) H₂ (г) + N₂ (г) + O₂ (г) = HNO₃ (ж);

б) H₂ (г) + N₂ (г) + O₃ (г) = HNO₃ (ж);

в) H₂ (г) + N₂ (г) + O₂ (г) = HNO₃ (ж);

г) H₂ (г) + N₂ (г) + O₂ (г) = HNO₃ (к);

д.) N₂O₅ (к) + H₂O(ж) = HNO₃ (ж)?

 

Решение. При 298,15 К стандартными состояниями для простых веществ будут H₂ (г), O₂ (г) и N₂ (г), а для азотной кислоты - жидкость (хотя можно говорить и о стандартных термодинамических функциях, например, и HNO₃ (г) при этой температуре). Поэтому лишь процесс "в" строго отвечает названному термину.

 

Пример 3. Определить величину стандартной энтальпии образования C₃H₈ (г)^, если стандартные энтальпии образования CO₂ (г) и Н₂О (ж) равны соответственно –393,5 и –285,8 кДж/моль, а стандартная энтальпия сгорания С₃Н₈ (г) составляет –2219,9 кДж/моль.

 

Решение. Запишем уравнение процесса, соответствующего термину "стандартная энтальпия образования С₃Н₈ (г)":

 

3C (к, графит) + 4H₂ (г) = C₃H₈ (г); .

 

Для определения Н воспользуемся 2-м следствием из закона Гесса (соотношение 1.12):

=3H⁰_сгорС (к, графит) + 4H⁰_сгорH₂(г) – H⁰_сгор.C₃H₈ (г).

Далее обратим внимание, что стандартные энтальпии образования СО₂(г) и Н₂O(ж) есть не что иное, как стандартные энтальпии сгорания графита
и водорода. Следовательно:

=3H⁰_обрСO₂ (г) + 4H⁰_обрH₂O (ж) – H⁰_сгорC₃H₈ (г) =

= 3(–393,5) + 4(–285,8) – (–2219,9) = – 103,8 кДж/моль.

 

Пример 4. Энтальпия растворения Na₂SO₄ (к) в воде с образованием раствора состава Na₂SO₄ (к)  400 H₂O составляет –1,5 кДж/моль, а энтальпия присоединения воды к Na₂SO₄ (к) c образованием Na₂SO₄ 10H₂O (к) равна –82,0 кДж/моль. Определить энтальпию растворения Na₂SO₄10H₂O (к) в воде
с образованием раствора состава Na₂SO₄ 400 H₂O.

 

Решение. Запишем условие задачи в виде термохимических уравнений:

 

а) Na₂SO₄ (к) + 400 H₂O (ж) = Na₂SO₄ (р-р, Na₂SO₄400H₂O); H₁;

б) Na₂SO₄ (к) + 10 H₂O (ж) = Na₂SO₄10H₂O (к); H₂;

в) Na₂SO₄10H₂O (к) + 390 H₂O (ж) = Na₂SO₄ (р-р, Na₂SO₄400H₂O); H_Х.

 

Как видно, искомое (третье) уравнение получается путем вычитания второго термохимического уравнения из первого, следовательно:

 

H_Х = H₁–H₂ = 1,5 – (–82,0) = 80,5 кДж.

 

Пример 5. На основе справочных данных определить, в каком случае в стандартных условиях выделится больше теплоты – при сгорании 2 моль CH₄ или 1 моль C₂H₆?

 

Решение. Термохимические уравнения процессов горения:

 

СH₄ (г) + 2O₂ (г) = CO₂ (г) + 2H₂O (ж);

С₂H₆ (г) + 3,5O₂ (г) = 2CO₂ (г) + 3H₂O (ж).

 

Выписываем из справочных данных стандартные энтальпии образования СО₂(г), H₂O(ж), CH₄(г) и C₂H₆(г), пользуясь 1-м следствием из закона Гесса, вычисляем энтальпии написанных процессов, то есть стандартные энтальпии сгорания CH₄(г) и C₂H₆(г):

 

H⁰_сгорСH₄ (г) = H⁰_обрCO₂(г) + 2H⁰_обрH₂O(ж) – H⁰_обрСH₄ (г) – 2H⁰_обрO₂(г) =
= – 393,5 + 2(–285,8) – (–74,8) – 20 = –890,3 кДж;

H⁰_сгорС₂H₆ (г) = 2H⁰_обрCO₂(г) + 3H⁰_обрH₂O(ж) – H⁰_обрС₂H₆ (г) –
– 3,5H⁰_обрO₂(г) = 2(–393,5) + 3(–285,8) – (–84,7) – 3,50 = – 1273,9 кДж.

 

Из полученных величин следует, что при сгорании 2 моль CH₄(г) выделяется теплоты больше, чем при сгорании 1 моль C₂H₆(г).

 

Пример 6. Вычислить среднюю энтальпию связи С–Н в метане на основе следующих термохимических данных:

 

1) C (к,графит) + 2H₂ (г) = CH₄ (г), = –74,8 кДж;

2) H₂ (г) = 2H (г), = 436,0 кДж;

3) C (к,графит) = C (г) , =715,1 кДж.

 

Решение. Согласно определению средняя энтальпия связи С–Н в СН₄ – это часть энтальпии следующего процесса:

CH₄ (г) = C (г) + 4H (г);= 4C–H.

 

Это уравнение может быть получено путем сложения третьего уравнения с удвоенным вторым уравнением и вычитанием из этой суммы первого уравнения, следовательно:

 

= 715,1 + 2(436,0)–(–74,8)=1661,9 кДж.

 

Отсюда:

H⁰_ср.С–H = =415,5 кДж.

 

Пример 7. Определить энтальпию связи С–С в этане на основе следующих данных:

Н_обрС₂Н₆(г) = –84,7 кДж/моль; Н_{сублимации}С(к,графит) = 715,1 кДж/моль;

Н _дисН_{2 на атомы} = 436,0 кДж; Н _ср. С–Н = 415,5 кДж/моль связи.

 

Решение. Запишем исходные данные в виде термохимических уравнений:

 

1) C (к,графит) + 3H₂ (г) = C₂H₆ (г), _обрC₂H₆(г);

2) C (к,графит) = C (г) , _{сублимации} C (к,графит);

3) H₂ (г) = 2H (г), _{диссоциации} H_{2 на атомы}.

 

Основой для нахождения искомой величины является термохимическое уравнение

C₂H₆ (г) = 2C (г) + 6H (г);

 

При распаде на атомы 1 моль С₂Н₆(г) будет разорвано 1 моль связей С–С и 6 моль связей С–Н, следовательно:

 

= + 6.

 

С другой стороны, может быть найдена на основе исходных термохимических данных, а именно – искомое уравнение получается путем сложения удвоенного второго уравнения с утроенным третьим уравнением и вычитания из полученной суммы первого уравнения, отсюда:

 

=2+3–=2715,1 + 3(436,0) – (–84,7) = 2822,9 кДж.

 

Находим теперь энтальпию связи С–С в этане:

 

= 2822,9 – 6(415,5) = 329,9 кДж/моль связи.

 

1.3. Энтропия

 

Пример 1. В каком из следующих процессов следует ожидать наибольшего и наименьшего изменения энтропии:

 

1) H₂ (г) + 0,5O₂ (г) = H₂O (ж);

2) H₂ (г) + 0,5 O₂ (г) = H₂O (г);

3) C₂H₆ (г) + 3,5O₂ (г) = 2 CO₂ (г) + 3 H₂O (г);

4) KClO₃ (к) = KCl (к) + 1,5 O₂ (г).

 

Решение. Знак и величину S процесса можно оценить, не производя вычислений, если вспомнить, что энтропия газа существенно больше энтропии жидкости и тем более – кристаллического вещества. Поэтому, определяя, насколько число молей газообразных веществ в правой части уравнения больше числа молей газообразных веществ в левой части уравнения, приходим к выводу, что наибольшая положительная энтропия характеризует четвертый процесс. Энтропии первого и второго процессов отрицательны, наибольшая отрицательная энтропия соответствует первому процессу.

 

Пример 2. Пользуясь справочными данными, определить стандартную энтропию образования K₂Cr₂O₇ (к).

 

Решение. Искомая величина – это S^о следующего процесса:

 

2K (к) + 2Cr (к) + 3,5 O₂ (г) = K₂Cr₂O₇ (к).

 

Эта величина может быть найдена на основе соотношения (1.18):



S⁰ = S⁰ K₂Cr₂O₇ (к) – 2S⁰ K (к) – 2S⁰ Cr (к) – 3,5S⁰ 0₂ (г) =
= 291 – 264,48 – 223,6 – 3,5205,0 = – 603,1 Дж/К.

 

Пример З. Пользуясь справочными данными, определить возможность самопроизвольного протекания при 298,15 К следующих процессов в изолированных системах:

 

1) KClO₃ (к) = KCl (к) +1,5 O₂ (г);

2) N₂ (г) + 2H₂ (г) + Cl₂ (г) = NH₄Cl (к).

 

Решение. Для изолированных систем критерием самопроизвольного течения процесса является положительное значение энтропии. Поэтому, пользуясь справочными данными, вычисляем для указанных процессов



= S⁰ KCl (к) + 1,5S⁰ O₂ (г) – S⁰ KClO₃ (к) =
= 82,6 + 1,5205,0 – 143,0 = 247,1 кДж/К;

= S⁰ NH₄Cl (к) – 0,5S⁰ N₂ (г) – 2S⁰ H₂ (г) – 0,5S⁰ Cl₂ (г) =
= 95,8 – 0,5191,5 – 2130,5 – 0,5223,0 = – 372,5 Дж/К.

 

В результате делаем вывод, что в изолированной системе первый процесс разрешен в самопроизвольном течении, а второй - запрещен.

 

1.4. Энергия Гиббса

1.5. Критерий самопроизвольного протекания процессов

 

Пример 1. На основе справочных данных проанализировать вопрос о возможности самопроизвольного протекания следующего процесса при 298,15 К в стандартных условиях:

 

NaH (к) + H₂O (ж) = NaOH (к) + H₂ (г).

 

Решение. Вычисляем стандартную энергию Гиббса данного процесса по соотношению (1.22):

G⁰=G⁰обрH₂(г) + G⁰обрNaOH (к) – G⁰обрH₂O (ж) – G⁰обрNaH (к) =
= 0 + (–495,9) – (–285,8) – (–56,4) = –153,7 кДж.

Поскольку G отрицательно, то данный процесс может самопроизвольно протекать при 298,15 К в стандартных условиях.

Пример 2. Почему многие соединения, имеющие Gобр > 0, могут быть получены и даже порой оказываются сравнительно стабильными?

 

Решение. Действительно, соединения, имеющие Gобр > 0, могут самопроизвольно распадаться на простые вещества (G такого процесса отрицательно!), однако скорость подобного распада может оказаться незначительной и подобные соединения оказываются сравнительно стабильными. В таких случаях говорят о термодинамически неустойчивых, но устойчивых кинетически соединениях. Примеры таких соединений: H₂Te, SiH₄, NO₂.

 

Пример 3. На основе расчетов термодинамических величин покажите, чем эффективнее восстанавливать при 298,15 К Сr₂O₃ (к) до металла – алюминием или магнием?

 

Решение. Для ответа на поставленный вопрос, очевидно, необходимо вычислить G^о двух процессов:

 

1) Cr₂O₃(к) + 3Mg(к) = 3MgO(к) + 2Cr(к);

2) Cr₂O₃(к) + 2Al(к) = Al₂O₃(к) + 2Cr(к);

G⁰₁= 2G⁰обрCr(к) + 3G⁰обрMgO(к) – 3G⁰обрMg(к) – G⁰обрCr₂O₃(к) =

= 3G⁰обрMgO(к) – G⁰обрCr₂O₃(к) = 3(–569,3) – (–1059,0) = – 648,9 кДж;

G⁰₂= G⁰обрCr(к) + G⁰обрAl₂O₃(к) – 2G⁰обрAl(к) – G⁰обрCr₂O₃(к) =

= G⁰обрAl₂O₃(к) – G⁰обрCr₂O₃(к) = – 1582,3 – (–1059,0) = – 523,3 кДж.

 

Самопроизвольное восстановление Сr₂O₃(к) до Сr(к) при 298,15 К возможно и Mg, и А1; учитывая, что G⁰ процесса с Mg более отрицательно, можно сказать, что восстановление магнием более эффективно.

 

Пример 4. На основе справочных данных оценить температуру восстановления WO₃(к) водородом.

 

Решение. Для начала определим термодинамические функции процесса восстановления при 298,15 К:

 

WO₃(к) + 3H₂(г) = W(к) + 3H₂O(г);

 

G⁰_298,15 = 3G⁰обрH₂O(г) + G⁰обрW(к) – 3G⁰обрH₂(г) – G⁰обрWO₃(к) =

= 3G⁰обрH₂O(г) – G⁰обрWO₃(к) = 3(–228,6) – (–763,8) = – 78,0 кДж;

H⁰_298,15= 3H⁰обрH₂O(г) + H⁰обрW(к) – 3H⁰обрH₂(г) – H⁰обрWO₃(к) =

= 3H⁰обрH₂O(г) – H⁰обрWO₃(к) = 3(–241,8) – (–842,7) = 117,3 кДж;

S⁰_298,15= 3S⁰H₂O(г) + S⁰W(к) – 3S⁰H₂(г) – S⁰WO₃(к) =

= 3188,7 + 32,7 – 3130,5 – 76 = 131,3 Дж/К.

 

Как видно, самопроизвольное течение процесса при 298,15 К невозможно. Однако, принимая во внимание положительное значение энтропии процесса, следует ожидать, что с ростом температуры отрицательный энтропийный вклад (–ТS⁰298,15K) будет увеличиваться и при некоторой температуре превысит положительное значение энтальпии процесса, а энергия Гиббса станет отрицательной. Границей начала самопроизвольного протекания процесса будет G⁰_T = 0. Поскольку информация о температурной зависимости величин Н⁰ и S⁰ отсутствует, примем в первом приближении, что они неизменны с ростом температуры, то есть:

 

Н⁰_T  Н⁰₂₉₈; S⁰_T  S⁰₂₉₈.

 

Иными словами, строгое термодинамическое соотношение

 

G⁰_T = Н⁰_T – TS⁰_T

 

переходит в приближенное

 

G⁰_T  Н⁰_298,15 – TS⁰_298,15 .

 

Полагая G⁰_T = 0, вычисляем соответствующую температуру:

 

H⁰_298,15 – TS⁰_298,15 = 0;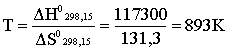

или 620⁰С.

 

Таким образом, при температуре выше 620°С возможно самопроизвольное течение процесса восстановления WO₃(к) водородом.

 

1.6. Изменение энергии Гиббса в окислительно-восстановительных реакциях

 

Пример 1. Пользуясь таблицей величин стандартных электродных потенциалов, приведите примеры нескольких окислителей, позволяющих перевести соединения Mn⁺² в соединения Mn⁺⁷.

 

Решение. Величина электродного потенциала для системы

MnO₄^– + 8H⁺ + 5ē = Mn²⁺ + 4H₂O

равна 1,51 В. Поскольку φ⁰= Е⁰окисл – Е⁰восст, а критерием самопроизвольного протекания ОВР в стандартных условиях является φ⁰ > 0, то любое вещество – окислитель, стандартный электродный потенциал для которого превышает 1,51 В, в принципе должен окислять ион Mn²⁺ до иона МnO₄^–
в кислой среде. Таковыми являются, например, ион Со³⁺, персульфаты, озон, фтор. Это подтверждается значениями величин электродных потенциалов:

Co³⁺ + ē = Co²⁺; E⁰ = 1,82 В;

S₂O₈^2– + 2ē = 2SO₄^2–; E⁰ = 2,01 В;

O₃ + 2H⁺ +2ē = O₂+H₂O; E⁰ = 2,07 В;

F₂ + 2H⁺ + 2ē =2HF; E⁰ = 3,06 В.