Конспект лекций. Конспект лекций, задачи и упражнения
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
2.1. Устойчивое и кажущееся равновесие, смещение равновесия 2.2. Количественные характеристики равновесия Пример 1. В равновесной системе при некоторой температуре равновесные концентрации составили: [CH4]равн = 0,6 моль/л, [O2]равн = 0,4 моль/л, [CO]равн = 0,5 моль/л. Найти начальные концентрации исходных веществ и равновесную концентрацию водорода, полагая, что в начальный момент концентрации СО и H2 были равны нулю. Решение. Поскольку в начальный момент течения процесса СО и Н2 отсутствовали, то, как видно из уравнения реакции, равновесная концентрация водорода будет в два раза больше равновесной концентрации СО, то есть составит 1 моль/л. Начальные концентрации СН4 и О2 будут равны равновесным плюс концентрации этих веществ, израсходованные на образование СО и Н2. Как следует из уравнения, на образование 0,5 моль/л СО должно быть израсходовано столько же СН4 и в 2 раза меньше О2. Отсюда находим: [CH4]нач = [CH4]равн + [CH4]изр = 0,6 + 0,5 = 1,1 моль/л; [O2]нач = [O2]равн + [O2]изр = 0,4 + = 0,65 моль/л. Пример 2. При некоторой температуре константа равновесия системы равна 2. Определить равновесную концентрацию PCl5 (г), если начальные концентрации PCl3, H2 и PCl5 составляли соответственно 3, 2, 0 моль/л. Решение. Пусть равновесная концентрация PCl5 (г) составляет Х моль/л; тогда равновесные концентрации PCl3 (г) и Cl2 (г) составят соответственно (3–Х) и (2–X) моль/л. Подставляем эти величины в выражение для константы равновесия: Корнями полученного квадратного уравнения будут: Х1 = 4, Х2 = 1,5. Первый корень в рамках условия задачи не имеет смысла, таким образом, равновесная концентрация PCl5 (г) составляет 1,5 моль/л. Пример 3. В каком мольном соотношении были смешаны в начальный момент СО2 (г) и Н2 (г), если константа равновесия составляет 2, а к моменту наступления равновесия 80% водорода превратилось в воду. Начальные концентрации СО и Н2О были равны нулю, объем системы постоянен. Решение. Пусть число молей H2 в начальной смеси было 1, а СО2 – Х моль. В момент равновесия [H2O]равн = [CO]равн = 0,8 моль/л (для простоты расчетов примем объем реакционной смеси равным 1 л), равновесные же концентрации исходных веществ составят: [H2]равн = 1 – 0,8 = 0,2 моль/л, [CO2]равн = (Х – 0,8) моль/л. Подставляем эти значения в выражение для константы равновесия: Решением этого уравнения будет значение Х = 2,4. Таким образом, СО2 и Н2 в начальный момент были смешаны в мольном соотношении 2,4 : 1. Пример 4. Пользуясь справочными данными, определить равновесную концентрацию N2O4 (г) при 298,15 К в системе если начальные концентрации составляли: [NO2]нач=5; [N2O4]нач=2 моль/л. Решение. Определим первоначально константу равновесия в указанной системе на основе соотношения (2.12): G° = G0обрN2O4 (г) – 2G°o6pNO2 (г) = 98,4 – 2·51,6 = –4,8 кДж. G0 = - RTlnKравн = –8,31·298,15 lnK равн 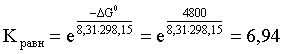 Пусть к моменту равновесия концентрация N2О4 (г) повысилась на Х моль/л по сравнению с исходной. Соответственно равновесные концентрации веществ составят: [N2O4] равн = (2+x) моль/л; [NO2] равн = (5–2x) моль/л. Подставляем эти величины в выражение для константы равновесия: 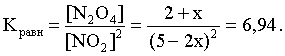 Решением полученного уравнения будут корни x1=2,92 и x2=2,12. Условию задачи удовлетворяет только значение 2,12, таким образом, равновесная концентрация N2O4 (г) составит 2 + 2,12 = 4,12 моль/л. Пример 5. На основе справочных данных оценить равновесное давление СО2 в системе СаСО3(к) = CaO(к) + CO2(г) при 1000°С. Решение. Константа равновесия в указанной системе будет равна равновесному давлению углекислого газа, так как концентрации кристаллических СаСО3 и СаО постоянны и равны единице. Для вычислений при температурах, отличных от 298,15 К, необходимо прибегать к какому-либо приближению. Как уже говорилось в тексте, таким приближением наиболее часто является допущение о независимости величин Н0 и S0 от температуры и использование приближенного уравнения: G0T 0298,15S0298,15 . Вычисляем по нему значение G0 для рассматриваемого процесса при 10000С (величины 0298,15 иS0298,15 для этого процесса найдены в разделе 1.5): G01273,15 = 178,4 – 1273,15160,5/1000 = –25,9 кДж. Далее находим равновесное давление углекислого газа по следующим соотношениям: G0T = - RTlnKравн = -RTlnPCO2 ; 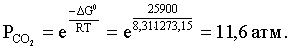 Пример 6. Для системы константа равновесия при Т = 300 К составляет 0,030, a S0 составляет 119 Дж/К. Найти Н0 для указанного процесса. Решение. Зная константу равновесия, легко найти G0 процесса G0 = - RTlnKравн = -RTln 0,030 = 8,7 кДж. Затем по известному термодинамическому соотношению находим H0 этого процесса: G0 =0S0; 0 =G0S0 = 8,7 + 119·300/1000 = 44,4 кДж. 3. НЕКОТОРЫЕ РАВНОВЕСИЯ В РАСТВОРАХ 3.1 Образование растворов, растворимость Растворами называют системы, в которых одно или несколько веществ распределено в среде одного или нескольких веществ. Раствор представляет собой однофазную систему, состав которой в некотором интервале концентраций, температур и давлений может меняться непрерывно. Состояние растворов относится к любому агрегатному состоянию – твердые растворы, например, сплавы металлов; жидкие – наиболее многочисленная группа; газовые, например, воздух. Идеально чистых веществ не может быть, поэтому и индивидуальные вещества могут быть отнесены к растворам. Процесс образования растворов – самопроизвольный, поэтому энергия Гиббса растворения отрицательна. Это возможно при эндотермическом растворении лишь в случае положительного значения энтропии растворения, при этом также должно выполняться TS > H. При экзотермическом растворении наиболее благоприятен случай с положительной энтропией растворения. При экзотермическом растворении самопроизвольно пойдут и процессы растворения с отрицательной энтропией при выполнении условия |TS| < |H|. При образовании растворов ситуация с Sраств > О широко распространена, так как происходит распределение частиц растворяемого вещества в большом количестве растворителя, что ведет к резкому росту неупорядоченности в системе. При росте концентрации происходит дальнейшее растворение растворяемого вещества. Растворы, в которых возможно дальнейшее самопроизвольное растворение, называются ненасыщенными. Наконец, при дальнейшем растворении достигается концентрация, при которой энергия Гиббса растворения достигает минимума. Полученный раствор вобрал в себя максимум при данных условиях растворенного вещества, он называется насыщенным раствором. Насыщенный раствор термодинамически устойчив и находится в равновесии с растворяемым веществом. Значение концентрации насыщенного раствора называется растворимостью. Значение растворимости может быть найдено по термодинамическим данным. Например, требуется найти концентрацию (активность) насыщенного раствора вещества А в данном растворителе. Для равновесия константа равновесия имеет вид: (3.1) С другой стороны, для указанного процесса: ΔGo = ΔGoобрA(р-р, ст.с) – ΔGoобрA(к) = –RTlnKравн = –RTlnA(нас.р-р) . (3.2) Можно получить и растворы, концентрация растворенного вещества в которых превышает концентрацию насыщенного раствора. Это – пересыщенные растворы. Поскольку растворение вещества в насыщенном растворе невозможно (ведет к положительному значению энергии Гиббса), получить пересыщенный раствор растворением вещества в насыщенном растворе нельзя. Обычно пересыщенные растворы получают, охлаждая насыщенные при более высокой (другой) температуре растворы. При этом энергия Гиббса уменьшится, но не настолько, чтобы раствор оставался равновесным. Пересыщенные растворы – это системы в кажущемся равновесии. Понятия растворитель, растворенное вещество, концентрированный или разбавленный раствор условны. Так концентрированным водным раствором будут считаться 6 мас.% раствор КМnО4, 98 мас.% раствор Н2SO4, 35 мас.% раствор NаCl. Основными способами выражения концентраций растворов являются: массовая, мольная, объемная (для газовых растворов) доля растворенного вещества или растворителя и соответственно массовый, мольный или объемный процент: молярность, нормальность, титр и моляльность. Массовая доля компонента раствора ω равна отношению массы этого компонента к массе раствора, то есть к сумме масс всех компонентов раствора, включая растворитель. Мольная доля компонента раствора равна отношению числа молей этого компонента к сумме числа молей всех компонентов раствора. Аналогично, для газовых растворов объемная доля компонента равна отношению объема этого компонента к сумме объемов всех компонентов газовой смеси. Массовая (мольная, объемная) доля компонента, умноженная на 100, называется массовым (мольным, объемным) процентом. Молярность М раствора определяется как число молей (количество вещества) растворенного вещества в 1 л раствора. Нормальность Н раствора равна числу молей эквивалентов растворенного вещества в 1 л раствора (см. раздел 6, с. 130). Титр Т равен числу граммов растворенного вещества, находящихся в 1 мл раствора (1 мл = 1 см3). Отметим, что размерность титра и плотности совпадают. Моляльность m раствора равна числу молей растворенного вещества, приходящихся на 1 кг растворителя. При образовании растворов в общем случае происходит изменение свойств и растворителя, и растворенного вещества, что связано с различными силами взаимодействия. Их можно подразделить на две группы – неспецифические (общие для всех) и специфические (индивидуальные). К неспецифическим относят электростатическое и ион-дипольное взаимодействия, силы металлической связи, силы Ван-дер-Ваальса (силы межмолекулярного взаимодействия). Все названные взаимодействия характеризуются как дальнодействующие. К специфическим взаимодействиям относят силы химической связи (водородные, донорно-акцепторные и т.п.). Они являются короткодействующими. К короткодействующим относятся также силы отталкивания. В растворах в разной степени имеют место физические и химические взаимодействия. Продуктами химического взаимодействия являются сольваты (в воде – гидраты), представляющие собой соединения переменного состава между частицами растворенного вещества и растворителя. Прочные сольваты удается выделить из раствора, например, кристаллогидраты. 3.2 Равновесие диссоциации электролитов Количественной характеристикой диссоциации является степень диссоциации α, равная отношению числа распавшихся на ионы молекул к общему их числу. Ее обычно выражают либо в долевом исчислении, либо в процентах. Например, если из 100 молекул 27 распалось на ионы, то степень диссоциации электролита составляет 0,27 или 27%. Современные представления о диссоциации электролитов предполагают помимо процесса диссоциации на ионы разнообразные процессы ионной ассоциации, то есть образование из индивидуальных ионов ионных пар, тройников и т.д. Соответственно различают ионизирующую и диссоциирующую способности растворителей. Собственно представления об образовании в растворах электролитов ионных пар или более сложных частиц являют собой применение к данным системам широко распространенных в химии представлений о комплексообразовании. Диссоциирующая сила растворителя определяется главным образом уменьшением электростатического взаимодействия, то есть значением диэлектрической проницаемости данного растворителя. Тогда как ионизирующая способность растворителя определяется не величиной диэлектрической проницаемости, а способностью молекул растворителя к специфической сольватации за счет донорно-акцепторного взаимодействия. Поэтому хорошо диссоциирующий растворитель не всегда является сильно ионизирующим. Вода обладает как ионизирующей, так и диссоциирующей способностью. В растворителях с диэлектрической проницаемостью меньше 10 практически нет свободных ионов, а при диэлектрической проницаемости свыше 40 для растворов электролитов концентации не ниже 0,01 М степень диссоциации, как правило, превышает 50%. В промежуточной области значений диэлектрической проницаемости в растворе в общем случае есть ионы и ионные пары, соотношение между ними определяется размерами и зарядами ионов и природой растворителя. Современные представления о растворах электролитов опираются на концепцию ассоциированных (α < 1) и неассоциированных (α = 1) электролитов. В последнем случае следует говорить о полной диссоциации электролита с определенной точностью, так как последовательное применение учения о равновесии запрещает представления о действительно полной диссоциации электролита. Под ассоциированными электролитами понимают недиссоциированные молекулы, разнообразные ионные ассоциаты и комплексы. Для водных растворов до сих пор широко используются представления о сильных и слабых электролитах, восходящие к создателю теории электролитической диссоциации С. Аррениусу. Сильными электролитами считают те, для которых условно принимают = 1 при любых концентрациях. К таким электролитам относят все средние соли; кислоты: галогеноводородные (кроме HF), азотную, хлорную, серную (только по первой ступени); основания: все гидроксиды щелочных металлов, гидроксиды кальция, стронция и бария. Еще раз подчеркнем, что полная диссоциация этих электролитов и тем более при любых концентрациях является фактически постулатом. Многие из перечисленных электролитов не только не распадаются полностью на ионы при любых концентрациях, но даже в разбавленных растворах имеют значения существенно меньше единицы. Так например, хлорид алюминия при молярности раствора 0,02 имеет степень диссоциации 20%. Иными словами, при указанной концентрации 80% ионов Аl3+ связаны в ионную пару АlСl2+. К слабым электролитам в водных растворах относят кислоты: угольную, сернистую, сероводородную, серную (по второй ступени), ортофосфорную, фтористоводородную, все карбоновые кислоты; основания: гидроксиды магния, бериллия, алюминия, аммония, все гидроксиды d-элементов. Константа равновесия диссоциации электролита: (3.3) называется константой диссоциации: 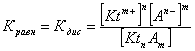 (3.4) (3.4)Формально Кдис для неассоциированного (сильного) электролита равна бесконечности. Для слабых электролитов эта величина конечна. Разумеется, в выражении термодинамической константы диссоциации должны фигурировать величины активностей, а не концентраций. Рассмотрим равновесие ступенчатой диссоциации электролитов на примере ортофосфорной кислоты: 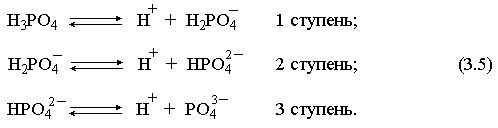 Отрыв протона от анионов H2PO4– и HPO42– происходит, несомненно, в меньшей степени, чем отрыв протона от нейтральной молекулы H3РО4. Кроме того, ионы водорода, образовавшиеся в первой ступени диссоциации, подавляют вторую ступень диссоциации, ионы водорода, образовавшиеся в первой и второй ступенях, подавляют третью ступень диссоциации. В результате реально диссоциация протекает лишь по первой ступени. Например, для водных растворов неорганических кислот, являющихся слабыми электролитами и диссоциирующими ступенчато, степень диссоциации по последующей ступени меньше степени диссоциации по предыдущей ступени в сотни раз. Это находит свое отражение в величинах констант ступенчатой диссоциации. Так для H3PO4 при 298,15 К они равны: 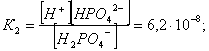 (3.6) (3.6)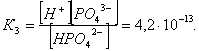 Из изложенного вытекает вывод, что диссоциацию любого слабого электролита, независимо от того, диссоциирует он ступенчато или нет, можно смоделировать равновесием диссоциации симметричного электролита: Пусть общая концентрация электролита KtA составляет с моль/л; степень диссоциации при этой концентрации равна . Тогда равновесные концентрации катиона, аниона и недиссоциированного электролита составят: [Ktn+]=[An-]=c; [KtA]=c–c Подставляем эти соотношения в выражение для константы диссоциации: Соотношение (3.8), связывающее константу диссоциации с концентрацией электролита и степенью его диссоциации носит название закона разбавления Оствальда. Зачастую степень диссоциации электролита мала ( << 1), тогда выражение (3.8) упрощается: Кравн а2с (3.9) 3.3. Шкала термодинамических функций образования ионов в водных растворах Для теории растворов электролитов большое значение имеет понятие "бесконечно разбавленный раствор". Это такой раствор, в котором 1 моль растворенного вещества приходится на бесконечно большое число молей растворителя. Бесконечно разбавленный раствор обладает следующими свойствами. Во-первых, любой электролит в нем полностью диссоциирован на ионы. Во-вторых, поскольку между ионами в таком растворе бесконечно большие расстояния, то взаимодействие между ними полностью отсутствует. Другими словами, в бесконечно разбавленном растворе ионы ведут себя независимо, и любое свойство электролита будет аддитивно слагаться из свойств составляющих его ионов. Любое свойство индивидуального иона, например термодинамическое, не может быть объективно определено. В таких ситуациях (см., например, раздел 1.6) прибегают к построению шкалы относительных величин, в которой значение рассматриваемого свойства для одной из систем постулируется, а значения свойства других систем отсчитываются от принятого значения. В частности для водных растворов электролитов шкала термодинамических функций образования ионов строится на основе следующих допущений: H0обр H+(р-р, H2O) = 0; G0обр H+(р-р, H2O) = 0; (3.10) S0 H+(р-р, H2O) = 0. Поскольку понятие бесконечно разбавленного раствора используется в определении стандартного состояния для растворов (см. раздел 1.2), то правильнее (по крайней мере, в отношении величин G), следует писать не (р-р, H2O), а (р-р, ст.с.). Обратим внимание также на то, что хотя энтропии веществ могут быть только положительными (см. раздел 1.3), энтропии индивидуальных ионов, являющиеся относительными величинами, могут быть и отрицательными. Константа диссоциации любого электролита в принципе может быть найдена на основе соотношения (2.12), связывающего в данном случае стандартную энергию Гиббса процесса диссоциации электролита с константой равновесия, каковой и является константа диссоциации. В свою очередь стандартная энергия Гиббса процесса диссоциации электролита находится согласно закона Гесса как разность стандартных энергий Гиббса образования ионов и недиссоциированного электролита. Для последнего возникает проблема – с одной стороны, стандартное состояние для недиссоциированного электролита соответствует раствору со свойствами бесконечно разбавленного; с другой стороны, при бесконечном разбавлении любой электролит полностью распадается на ионы и говорить о недиссоциированном электролите вообще не приходится. Эта проблема решается введением для растворов дополнительного стандартного состояния – раствор, стандартное состояние, гипотетически недиссоциированный (р-р, ст.с., гип. недис.). Иными словами, электролит находится в растворе со свойствами бесконечно разбавленного, но при этом не диссоциирует на ионы. Например, необходимо определить константу диссоциации синильной кислоты при 298,15 К по термодинамическим данным. В соответствии с уравнением диссоциации G0дис = –RTlnКдис G0обр H+ (р-р, ст.с) + G0обр CN–(р-р, ст.с) – – G0обр HCN (р-р, cт.с., гип. недис) = 0 + 171,6 – 119,0 = 52,6 кДж находим константу диссоциации по соотношению: Кдис = = = 6,010–10 . Введение в раствор электролита общего с ним иона в соответствии с принципом Ле Шателье ведет к уменьшению степени диссоциации электролита. Так, например, растворение КСN в упоминавшемся растворе НСN ведет к уменьшению диссоциации. Остановимся еще дополнительно на термодинамических функциях образования растворов. Энтальпия образования раствора данного соединения определенной концентрации равна стандартной энтальпии образования этого соединения плюс энтальпия его растворения с образованием раствора нужного состава. Если происходит растворение с образованием бесконечно разбавленного раствора, то получаем стандартную энтальпию образования соединения в состоянии раствора. Напомним, если растворяемое соединение является электролитом, то его стандартная энтальпия образования равна сумме стандартных энтальпий образования ионов. 3.4 Равновесие растворения и диссоциации малорастворимого электролита Рассмотрим равновесие, устанавливающееся на границе малорастворимый электролит (кристаллический или аморфный) – насыщенный раствор этого соединения: насыщ. р-р насыщ. р-р В водных растворах все малорастворимые электролиты не ассоциированы. Другими словами, средняя стадия написанного равновесия отсутствует, равновесие упрощается: Соответствующая константа равновесия с учетом того, что концентрация индивидуального кристаллического вещества равна единице, принимает вид: Кравн = [Ktm+]n[An-]m = произведение растворимости (ПР). (3.13) Таким образом, произведение растворимости (ПР) есть константа равновесия растворения и диссоциации малорастворимого электролита. Оно численно равно произведению концентраций (активностей) ионов в степенях стехиометрических коэффициентов в насыщенном водном растворе данного малорастворимого электролита. Пусть при данных условиях растворимость электролита равна Р моль/л. Тогда в соответствии с равновесием (3.12) равновесные концентрации ионов в насыщенном растворе будут равны: [Ktm+] = nP; [An-] = mP. Подставляем эти значения в выражение (3.13): ПР = [Ktm+]n[An-]m = (nP)n(mP)m = nnmmPn+m . И, наконец, находим выражение, связывающее величину ПР с растворимостью данного малорастворимого электролита: (3.14) Поскольку величина ПР представляет собой константу равновесия (3.12), то ее значение легко может быть найдено по термодинамическим данным на основе следующих соотношений и величин: G0процесса = –RTlnПР = = nG0обрKtm+ (р-р, ст.с) + mG0обрAn-(р-р, ст.с) – G0обрKtnAm (к) (3.15) Обратимся теперь к следующей проблеме. Пусть слили растворы, содержащие катионы Ktm+ и анионы An-, могущие образовывать малорастворимое соединение. Необходимо определить – выпадет или нет осадок и каково условие выпадения осадка? Для того чтобы соединение выпало в осадок, необходимо, чтобы энергия Гиббса процесса (3.11) была положительна. Согласно соотношению (2.11) получаем для указанного процесса: G = –RTlnКравн + RTln[Ktm+]n[An-]m = –RTlnПР + [Ktm+]n[An-]m , где [Ktm+]n[An-]m = ПК. Под знаком логарифма стоят концентрации ионов, которые должны быть в гипотетическом растворе, полученном смешением растворов, содержащих ионы Ktm+ и An-, и в котором эти ионы не взаимодействуют. Стоящее под знаком логарифма произведение называют "произведение концентраций" (ПК), по форме оно совпадает с выражением ПР. Для выпадения осадка должно выполняться условие G > 0, отсюда получаем: (–RTlnПР + RTlnПК) > 0; RTlnПК > RTlnПР; ПК > ПР. (3.16) Соотношение (3.16) и выражает условие выпадения осадка. Очевидно, что условием растворения осадка будет соотношение ПК < ПР, а равенство ПК=ПР соответствует состоянию равновесия между малорастворимым соединением и его насыщенным раствором. В соответствии с принципом Ле Шателье введение одноименного иона в равновесную систему (3.11) ведет к смещению равновесия влево, то есть к уменьшению растворимости малорастворимого электролита. 3.5 Равновесие диссоциации воды, буферные растворы Вода диссоциирует крайне незначительно в соответствии с уравнением: Для простоты вместо иона гидроксония будем писать негидратированный ион, так как это не влияет на последующие выводы: Пользуясь термодинамическими данными и помня, что концентрация индивидуального жидкого вещества равна единице, находим термодинамическую константу обсуждаемого равновесия G0процесса = G0обрH+(р-р,ст.с) + G0обрOH-(р-р,ст.с) – G0обрH2O(ж) = = 0 – 157,32 – (–237,25) = 79,93 кДж; Кравн= = [H+][OH–]= KW – ионное произведение воды. (3.17) Замена активностей ионов на концентрации оправдана тем, что вода диссоциирует в очень незначительной степени. Действительно, при 298,15К концентрации ионов Н+ и ОН– в воде составляют 110–7 моль/л. В 1 л воды, имеющей массу 1000 г, содержится 1000/18 = 55,5 моль воды. Следовательно, отношение недиссоциированных молекул к диссоциированным составляет 55,5/10–7 = 555000000. Иными словами, из 555 миллионов молекул воды диссоциирует лишь одна! В соответствии с (3.17) ионное произведение воды при 298,15 К равно: КW = = = 1,010–14 ; [H+][OH–]=1,010-14 . (3.18) Логарифмируем выражение (3.18) и меняем знаки в обеих частях уравнения: lg[H+] + lg[OH–] = – 14; –lg[H+] – lg[OH–] = 14. В учебной и научной литературе для выражения маленьких величин используют отрицательную десятичную логарифмическую шкалу: рК = – lg К (читается "пе ка"). В соответствии с этим вводим величины рН и рОН, определяемые как: pH = –lg[H+]; pOH = –lg[OH–] . (3.19) Возвращаясь к предыдущим выкладкам, получаем, что для любого водного раствора при 298,15 К: рН + рОН = 14. (3.20) В воде в соответствии с уравнением ее диссоциации соответственно рН = рОН =7, это нейтральная среда. В кислых растворах [H+] >10–7 моль/л и рН<7 (рОН>7). В щелочных растворах [H+]<10–7 моль/л и рН>7 (рОН<7). Получить растворы с большой концентрацией кислоты не представляет труда, например, H2SO4 и HNO3 неограниченно растворимы в воде и можно приготовить их водные растворы практически любой молярной концентрации. Однако с ростом концентрации кислоты уменьшается степень ее диссоциации и реальных системах получить растворы с концентрацией ионов водорода, большей 10 моль/л, практически невозможно. Учитывая это, получаем интервал изменения величин рН: –1 < рН < 15. (3.21) Растворы с постоянным значением рН, не зависящим от разбавления и слабо зависящим от небольших добавок сильных кислот и оснований, называются буферными. Буферные растворы на кислую область – смеси растворов слабых кислот и их солей. Буферным раствором на щелочную область является смесь водного раствора аммиака (NH4ОН) и солей аммония. Продемонстрируем свойства буферного раствора на примере смеси уксусной кислоты и ацетата натрия. Уравнения диссоциации электролитов: 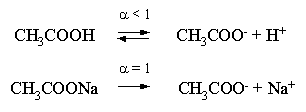 Диссоциация слабого электролита, уксусной кислоты, будет за счет диссоциации ацетата натрия подавлена так, что концентрация ацетат-иона будет практически полностью создаваться за счет диссоциации соли, а концентрация недиссоциированной уксусной кислоты фактически равна общей концентрации кислоты. Выражение для константы равновесия диссоциации уксусной кислоты: Кдис= [H+] Отсюда концентрация ионов водорода составляет: [H+] Кдис (3.22) Как видно из (3.22), при разбавлении буферного раствора водой концентрации кислоты и соли синхронно уменьшаются в одинаковое число раз, а их отношение, а значит и концентрация ионов водорода, останется неизменным. Добавление в буферную смесь нескольких капель концентрированного раствора НСl приведет к небольшому увеличению концентрации уксусной кислоты и уменьшению концентрации соли, а значение дроби скислоты/ссоли изменится мало. Аналогичная ситуация будет и при добавлении в буферную смесь нескольких капель концентрированного раствора едкого натра – несколько уменьшится концентрация уксусной кислоты и возрастет концентрация соли, а отношение скислоты/ссоли изменится мало. 3.6. Гидролиз солей Поляризационное взаимодействие катионов и анионов с сильно полярными молекулами воды ведет к особой химической реакции ионного обмена, называемой гидролизом солей. Качественную и количественную стороны гидролиза удобно рассматривать с позиции концепции сильных и слабых электролитов (неассоциированных и ассоциированных). Практически все электролиты, относящиеся к категории слабых в водных растворах (см. раздел 3.2), характеризуются тем, что равновесие их диссоциации смещено влево, в сторону недиссоциированных частиц. Иными словами, для них характерна не диссоциация, а наоборот – ассоциация, то есть связывание соответствующими анионами протонов, катионами – ионов ОН– в недиссоциированные частицы. А ионы Н+ и ОН– всегда имеются в воде за счет ее незначительной диссоциации. Рассмотрим более подробно происходящие процессы на примерах двух солей – CuCl2 и Na2CO3. Хлорид меди (II) является сильным электролитом, поэтому в водном растворе полностью диссоциирует на ионы: Гидроксид меди (II) относится к слабым электролитам (см. раздел 3.2), иными словами катион Cu2+ при наличии в растворе ионов ОН– будет активно связывать их в малодиссоциированную частицу СuОН+ , нарушая тем самым равновесие диссоциации воды:  В результате, согласно принципу Ле Шателье, усилится диссоциация воды и в растворе увеличится концентрация ионов водорода по сравнению с той, которая была в воде. Раствор становится кислым, его рН<7, подобная ситуация называется гидролизом по катиону. Разумеется, гидролиз хлорида меди может идти и дальше, по второй ступени: Однако, принимая во внимание то, что продукты гидролиза по первой ступени подавляют вторую ступень и то, что поляризационное взаимодействие иона Cu2+ с молекулами воды несравненно сильнее, чем иона CuOH+, приходим к следующему важному выводу. При наличии возможности протекания ступенчатого гидролиза, этот процесс реально протекает лишь по первой ступени. Сходная ситуация возникает и в растворе Na2COЗ. В результате полной диссоциации этой соли в растворе образуются ионы CO32–, являющиеся анионами слабой угольной кислоты. Этот ион при наличии в растворе протонов будет активно связывать их в малодиссоциированную частицу HCO3–, нарушая тем самым равновесие диссоциации воды:  В результате усилится диссоциация воды и в растворе увеличится концентрация ионов ОН– по сравнению с той, которая была в воде. Раствор стал щелочным, его рН > 7, в этом случае говорят о гидролизе по аниону. Справедливости ради следует отметить, что реальный механизм гидролиза несколько иной. Любые ионы в водном растворе гидратированы и поляризационное взаимодействие осуществляется между ионом и молекулами воды, составляющими его гидратную оболочку, например: Это уточнение никоим образом не изменяет сделанные выше выводы и не сказывается на дальнейших количественных выкладках. Таким образом, гидролизу подвергаются либо соли, содержащие катионы слабых оснований (гидролиз по катиону), либо соли, содержащие анионы слабых кислот (гидролиз по аниону). Если же катион и анион в молекуле соли являются ионами соответствующих сильного основания и сильной кислоты, то в растворе такой соли гидролиза нет, его рН 7. Если же соль содержит в своем составе катион слабого основания и анион слабой кислоты, то гидролиз в этом случае идет по двум направлениям и, как правило, глубоко. Что же касается кислотности такого раствора, то она будет определяться направлением преимущественного гидролиза. Способы усиления гидролиза солей: 1) разбавление раствора соли; 2) нагрев раствора, поскольку энтальпии гидролиза положительны; 3) добавление щелочи в раствор для усиления гидролиза по катиону, добавление кислоты в раствор для усиления гидролиза по аниону. Способы подавления гидролиза: 1) охлаждение раствора, 2) добавление кислоты в раствор для подавления гидролиза по катиону, добавление щелочи в раствор для подавления гидролиза по аниону. Рассмотрим количественные характеристики гидролиза. Таковыми являются, в первую очередь, степень и константа гидролиза. Степенью гидролиза (h) аналогично степени диссоциации называют долю гидролизо-ванных молекул по отношению к общему числу молекул. Константа гидролиза представляет собой константу равновесия процесса гидролиза. Выше было показано, что гидролиз протекает лишь по первой стадии. Первую стадию гидролиза по катиону можно записать в общем виде: Константа равновесия этого процесса – константа гидролиза равна: Кравн = Кгидр = 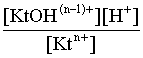 . (3.23) . (3.23)Домножаем числитель и знаменатель этого выражения на концентрацию иона ОН– и получаем: Кгидр = 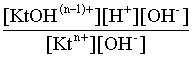 = (3.24) = (3.24)Таким образом, константа гидролиза по катиону равна отношению ионного произведения воды к константе диссоциации того самого слабого основания, чья соль подвергается гидролизу, или к константе диссоциации основания по соответствующей стадии. Вернемся к соотношению (3.23). Пусть общая концентрация гидролизующейся соли в растворе равна с моль/л, а степень ее гидролиза – h. Тогда, учитывая, что [KtOH(n-1)+] = [H+] и h= [H+]/с, получаем из соотношения (3.23): Кгидр = 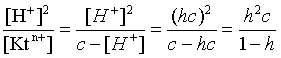 . (3.25) . (3.25)Соотношение (3.25) по форме совпадает с выражением закона разбавления Оствальда (3.8), что лишний раз напоминает о генетической связи процессов гидролиза и диссоциации. Первую стадию гидролиза по аниону можно записать в общем виде следующим образом: Константа равновесия этого процесса – константа гидролиза равна: Кравн = Кгидр = . (3.26) Домножаем числитель и знаменатель этого выражения на концентрацию иона Н+ и получаем: Кгидр = 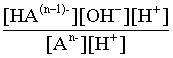 = . (3.27) = . (3.27)Таким образом, константа гидролиза по аниону равна отношению ионного произведения воды к константе диссоциации той самой слабой кислоты, чья соль подвергается гидролизу, или к константе диссоциации кислоты по соответствующей стадии. Обратимся снова к выражению (3.26). Преобразуем его, полагая, что общая концентрация соли в растворе равна с моль/л и, учитывая, что [HA(n–1)–] = [OH–]; h = [OH–] / c, получаем: Кгидр= 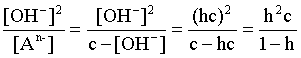 . (3.28) . (3.28)Выражения (3.23), (3.24) и (3.27), (3.28) являются достаточными для нахождения равновесных концентраций ионов, констант и степеней гидролиза в водных растворах гидролизующихся солей. Нетрудно догадаться, что константа гидролиза соли, подвергающейся гидролизу по катиону и аниону одновременно, равна отношению ионного произведения воды к произведению констант диссоциации слабого основания и кислоты или произведению констант диссоциации соответствующих стадий. Действительно, гидролиз соли по катиону и аниону одновременно можно представить в общем виде следующим образом: Константа гидролиза имеет вид: Кгидр= . (3.29) Домножаем числитель и знаменатель соотношения (3.29) на КW и получаем: Кгидр= 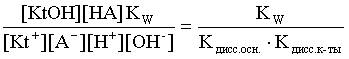 . (3.30) . (3.30)Пусть общая концентрация соли, гидролизованной одновременно по катиону и аниону, равна c моль/л, степень гидролиза составляет h. Очевидно, что [KtОН]=[HA]=hc; [Kt+]=[A–]=c–hc. Подставляем эти соотношения в выражение (3.29): Кгидр= 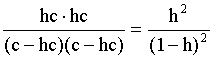 . (3.31) . (3.31)Получился любопытный результат – концентрация явным образом не входит в выражение константы гидролиза, иными словами, степень гидролиза соли, подвергающейся гидролизу по катиону и аниону одновременно, будет одной и той же при любых концентрациях соли в растворе. Найдем выражение для рН рассматриваемого раствора соли. Для этого числитель и знаменатель соотношения (3.29) домножим на концентрацию иона Н+ и преобразуем полученное выражение: Кгидр= 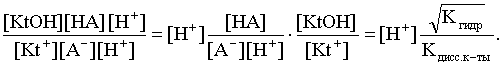 3.32) 3.32)Наконец, получаем: [H+]=Kдисс.к-ты. (3.33) Остановимся теперь на связи характеристик гидролиза и диссоциации в случае ступенчатого гидролиза. В качестве примера рассмотрим гидролиз уже упоминавшегося карбоната натрия. Равновесие гидролиза Na2CO3 по ступеням и соответствующие константы равновесия приведены ниже: 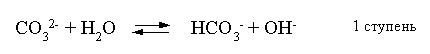 Кгидр(1) ====; 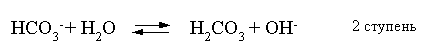 Кгидр(2) ===. Таким образом, первой ступени гидролиза соответствует последняя ступень диссоциации соответствующего слабого электролита и наоборот – последней ступени гидролиза соответствует первая ступень диссоциации электролита. При анализе вопроса о гидролизе кислых солей необходимо сопоставлять значения констант гидролиза и констант диссоциации анионов. Если константа гидролиза больше константы диссоциации кислого аниона, то гидролиз по аниону имеет место и раствор характеризуется рН > 7. Если же константа гидролиза меньше константы диссоциации соответствующего кислого аниона, то гидролиз подавлен, реально протекает лишь диссоциация кислого аниона и раствор соли имеет рН < 7. Выше отмечалось, что простейшим способом усиления гидролиза соли по катиону является введение в такой раствор щелочи. Аналогично для усиления гидролиза соли по аниону необходимо ввести в раствор кислоту. А что произойдет при сливании растворов двух солей, из которых одна гидролизована по катиону, а другая – по аниону, например, растворов Na2CO3 и CuCl2? Равновесия гидролиза в этих растворах: 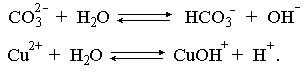 Как видно, гидролиз первой соли будет усиливать гидролиз второй и наоборот. В этом случае говорят о взаимном усилении гидролиза. Ясно, что в подобной ситуации образование продукта обменной реакции невозможно, должны образовываться продукты гидролиза. Состав их зависит от большого числа факторов: концентраций сливаемых растворов, порядка смешения, степени перемешивания и т.д. В рассматриваемой системе (и подобных ей) образуются основные карбонаты, в некотором приближении их состав можно рассматривать как ЭCO3Э(OH)2=(ЭOH)2CO3 . Уравнение протекающего процесса: 2CuCl2 + 2 Na2CO3 +H2O = (CuOH)2CO3 + CO2 + 4 NaCl . Аналогичные малорастворимые соединения будут получаться при взаимодействии растворимых карбонатов с солями любых двухвалентных металлов, гидролизованными по катиону. Если же соли не гидролизованы, то происходит обычный обменный процесс, например: BaCl2 + Na2CO3 = BaCO3 + 2 NaCl . В общем случае соли Ме3+ более гидролизованы, чем соли Ме2+, поэтому, если в обсуждаемом процессе CuCl2 заменить на соль Ме3+, то следует ожидать более сильного взаимного усиления гидролиза. И действительно, при сливании растворов солей Fe3+, Al3+, Cr3+ с раствором Na2CO3 наблюдается выделение углекислого газа и выпадение осадка гидроксида металла. Другими словами, в этом случае взаимное усиление гидролиза ведет к полному (необратимому) гидролизу, например: 2FeCl3 + 3Na2CO3 + 3H2O = 2Fe(OH)3 + 6NaCl + 3CO2 . Сходные процессы будут наблюдаться при смешении растворов солей Ме3+ с растворами других солей, гидролизованных по аниону, например: 2AlCl3 + 3Na2SO4 + 3H2O = 2Al(OH)3 + 3SO2 + 6NaCl Cr2(SO4)3 + 3Na2S + 6H2O = 2Cr(OH)3 + 3H2S + 3Na2SO4 . В отличие от солей гидролиз производных кислот – галогенангидридов, тиоангидридов – протекает глубоко и, зачастую, полностью (необратимо), например: SO2Cl2 + 2H2O = H2SO4 + 2HCl ; SOCl2 + H2O = SO2 + 2HCl ; COCl2 + H2O = CO2 + 2HCl ; BCl3 + 3H2O = H3BO3 + 3HCl ; PCl3 + 3H2O = H3PO3 + 3HCl ; CrO2Cl2 + 2H2O = H2CrO4 + 2HCl ; t CS2 + 2H2O = CO2 + 2H2S . Наконец, отметим особый случай гидролиза соединений Вi(III), Sb(III), солей d-элементов – с образованием оксосоединений, например: SbCl3 + H2O = SbOCl + 2HCl ; Bi(NO3)3 + H2O = BiONO3 + 2HNO3 ; Ti(SO4)2 + H2O = TiOSO4 + H2SO4 . Константа гидролиза как и любая другая константа равновесия может быть вычислена на основе термодинамических данных. Задачи и упражнения |
