Конспект лекций. Конспект лекций, задачи и упражнения

• Название: Конспект лекций, задачи и упражнения
• Анкор: Конспект лекций.docx
• Дата: 03.05.2018
• Размер: 0.51 Mb.
• Имя файла: Конспект лекций.docx
• Тип: Конспект; #18833
• страница: 3 из 10

Пример 2. Какие вещества (молекулы, ионы) не должны существовать в водном растворе?

 

Решение. Таковыми должны быть соединения, электродный потенциал которых для соответствующей электрохимической пары превышает
потенциал разложения воды

 

O₂ + 4H⁺ + 4ē = 2H₂O; E⁰ = 1,229 B.

 

Выпишем некоторые из них:

 

MnO₄^– + 8H⁺ + 5ē = Mn²⁺ + 4H₂O; E⁰ = 1,51 B;

BrO₃^– + 6H⁺ + 5ē = 0,5Br₂ + 3H₂O; E⁰ = 1,52 B;

Cr₂O₇^2– + 14H⁺ + 6ē = 2Cr³⁺ + 7H₂O; E⁰ = 1,33 B;

Co³⁺ + ē = Co²⁺; E⁰ = 1,82 B;

S₂O₈^2– + 2ē = 2SO₄^2–; E⁰ = 2,01 B.

 

Из приведенных цифр следует, что ионы MnO₄^–, Cr₂O₇^2–, BrO₃^–, S₂O₈^2– являются термодинамически неустойчивыми в водных растворах и должны окислять воду. Однако, кроме иона Со³⁺, остальные ионы кинетически устойчивы и реально существуют в водных растворах. Соединения же, дающие в водных растворах ион Со³⁺, окисляют воду.

 

Пример 3. Оценить условия, при которых серебро будет растворяться в минеральных кислотах.

 

Решение. Для того чтобы серебро растворялось в минеральных кислотах необходимо, чтобы процесс

2Ag + 2H⁺ = 2Ag⁺ + H₂

был самопроизвольным, то есть имел G < 0 или φ > 0. Согласно соотношениям (1.27, 2.16):

Ag⁺ + ē =Ag;

2H⁺ + 2ē = H₂;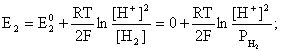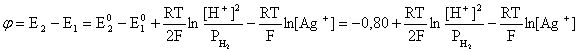



Проанализируем вопрос о том, какими должны быть величины [H⁺], и [Ag⁺] для того, чтобы выполнялось φ > 0. Пусть [Ag⁺] = 1, [H⁺] = 1, получаем: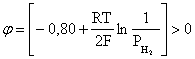

;

;

lg< –27,1; < 7,910^–28 атм.

 

Пусть [Ag⁺] = 1, = 1, получаем:

;

0,059 lg [H⁺] > 0,80;

lg [H⁺] > 13,6;

[H⁺] > 4,010¹³ моль/л.

 

Как видно, для осуществления указанного процесса необходимо мизерное парциальное давление водорода в системе (глубочайшее разрежение!), либо невероятно большая кислотность раствора. И то, и другое практически реализовать невозможно. Пусть = 1, [Н⁺] = 1, получаем:

;

 

0,059 lg [Ag⁺] < – 0,80;

lg [Ag⁺] < – 13,6;

[Ag⁺] < 2,510^-14 моль/л.

 

Таким образом, если в растворе поддерживать равновесную концентрацию ионов серебра на уровне, меньшем 10^-14 моль/л, то процесс растворения серебра в кислоте с [Н⁺] = 1 при =1 станет самопроизвольным. Поддерживать столь малую концентрацию ионов серебра в растворе возможно только лишь в присутствии лигандов, образующих прочные комплексные соединения с ионами серебра. Фактически в этом случае электродный потенциал E_Ag+/Ag смещается из области положительных значений к отрицательным величинам.

 

Пример 4. На примере комплексных соединений кобальта проанализировать возможность существования ионов Со²⁺ и Со³⁺ в водном растворе.

 

Решение. Стандартный электродный потенциал для пары Со³⁺/Со²⁺ в водном растворе составляет 1,82 В, что значительно превышает потенциал разложения воды. Иными словами ион Со³⁺ (гидратированный!) не может существовать в водном растворе – он будет окислять воду до О₂ и восстанавливаться до иона Со²⁺. С другой стороны, концентрационная зависимость этого потенциала выражается следующим выражением:

 

.

Из этого выражения видно, что чем меньше концентрация свободного (гидратированного!) иона Со³⁺ по сравнению с концентрацией иона Со²⁺ (гидратированного!), тем больше потенциал смещается в область отрицательных величин. Такая ситуация возникает практически всегда, когда
в растворе находятся лиганды, образующие комплексы более прочные, чем аквакомплексы. Так, в аммиачных растворах

 

[Co(NH₃)₆]³⁺ + ē = [Co(NH₃)₆]²⁺; E⁰=0,10 B.

 

В цианидных же растворах потенциал смещается настолько сильно в отрицательную область, что не только Со³⁺ не окисляет воду, а наоборот – комплексный ион [Сo²⁺(CN)₆]^4– восстанавливает воду, окисляясь до [Сo³⁺(CN)₆]^3–:

 

2 [Сo²⁺(CN)₆]^4– + 2H₂O = 2 [Сo³⁺(CN)₆]^3– + H₂ + 2OH^– .

 

Пример 5. На основе значений следующих стандартных электродных потенциалов:

Tl⁺ + ē= Tl; E⁰₁ = –0,34 B;

Tl³⁺ + 2ē = Tl⁺; E⁰₂ = 1,25 B

 

определить величину стандартного электродного потенциала для пары Tl³⁺/Tl.

 

Решение. Уравнения окислительно-восстановительных полуреакций не являются термохимическими и поэтому не позволяют выполнять над собой алгебраические операции. Включим написанные две полуреакции и искомую

Tl³⁺ + 3ē = Tl; E⁰_X

в реальные химические процессы, например, восстановления иона Tl³⁺ водородом и взаимодействия таллия с кислотой (протонами). Пусть все участники нижеследующих процессов находятся в стандартных состояниях. Тогда имеем:

 

а) 2Tl + 2H⁺ = 2 Tl⁺ + H₂ (2H⁺ + 2ē = H₂, E⁰ = 0 B)

G⁰_a= –2F(0–E⁰₁) = 2FE⁰₁;

б) Tl³⁺ + H₂ = Tl⁺ + 2H⁺

G⁰_б= –2F(E⁰₂ – 0) = –2FE⁰₂;

в) 2Tl³⁺ + 3H₂ = 2 Tl + 6H⁺

G⁰_в= –6F(E⁰_x – 0) = –6FE⁰_x .

 

Термохимическое уравнение "в" получается вычитанием уравнения "а" из удвоенного уравнения "б", таким образом:

 

G⁰_в =2G⁰_б – G⁰_а;

–6FE⁰_x = –4FE⁰₂ – 2FE⁰₁;

3E⁰_x=2E⁰₂+E⁰₁;

.

 

2. ХИМИЧЕСКОЕ РАВНОВЕСИЕ

 

2.1. Истинное и кажущееся равновесие, смещение равновесия

 

Равновесным называют такое состояние системы, которое не изменяется во времени, и эта неизменность не обусловлена протеканием какого-либо внешнего процесса. Равновесие остается неизменным, пока не меняются внешние условия. Различают истинное (устойчивое) и кажущееся (кинетическое) равновесие.

Истинное равновесие сохраняется неизменным не вследствие отсутствия процессов, а в силу протекания их одновременно в двух противоположных направлениях с одинаковой скоростью. Истинное равновесие имеет следующие признаки:

1. Если нет внешнего воздействия, то система неизменна во времени.

2. Система следует за любыми изменениями внешних условий, сколь угодно малыми они бы ни были, а если воздействие снято, то система возвращается в исходное состояние равновесия.

3. Состояние системы будет одинаковым независимо от того, с какой стороны она подходит к равновесию.

Кажущееся равновесие также неизменно во времени при отсутствии внешнего воздействия, однако второй и третий признаки для него не характерны. Примером системы в кажущемся равновесии является пересыщенный раствор: достаточно попадания соринки в такой раствор или встряхивания – и начинается выделение из раствора избыточного растворенного вещества. Другой пример – смесь водорода и кислорода при комнатной температуре: внесение в нее зажженной спички или катализатора неизбежно ведет к взрыву.

При изменении внешних условий равновесие изменяется сообразно новым условиям или, как говорят, смещается. Смещение равновесия подчиняется закономерности, называемой принципом Ле Шателье.

Он гласит: если на систему, находящуюся в устойчивом равновесии, воздействовать извне, изменяя одно из условий, определяющих состояние равновесия, то в системе усилится течение того процесса, который будет ослаблять оказываемое воздействие, а равновесие сместится в соответствующую сторону.

Повышение температуры равновесной системы усиливает течение эндотермического процесса, охлаждение – наоборот. Например, в системе

с ростом температуры равновесие диссоциации воды смещается вправо, то есть с повышением температуры усиливается диссоциация воды.

Изменение давления существенно сказывается лишь на равновесиях газовых систем. Увеличение давления для них ведет к смещению равновесия в сторону меньшего объема, падение давления – в сторону большего объема. Например, равновесие в системе

 

 

при увеличении давления смещается вправо, а при уменьшении – влево.

Увеличение концентрации исходных веществ ведет к смещению равновесия вправо (в сторону продуктов). Степень смещения равновесия при данном количестве вещества определяется величиной стехиометрического коэффициента.

Наконец, отметим, что введение в газовую систему, находящуюся при равновесии и имеющую постоянное давление, газа, не реагирующего ни с одним из компонентов, приводит к синхронному разбавлению всех участников. Следовательно, вопрос о смещении равновесия сводится к вопросу о влиянии уменьшения концентраций всех компонентов равновесной системы на положение равновесия. Согласно принципу Ле Шателье в этом случае смещение равновесия будет происходить в сторону большего объема (большего числа молей). Например, введение азота или аргона в равновесную систему

приведет к смещению равновесия влево.

 

2.2. Количественные характеристики равновесия

 

Методами термодинамики можно показать, что зависимость энергии Гиббса k-го компонента идеального газа от его парциального давления (Р_k) выражается соотношением (речь идет об абсолютном значении энергии Гиббса!):

. (2.1)

Для реального газа это соотношение принимает вид:

 

. (2.2)

 

Аналогично выражения для энергии Гиббса m-го компонента идеального и реального растворов имеют вид (речь идет об абсолютном значении энергии Гиббса!):

,

. (2.3)

 

Обратим внимание, что значения функций g_k(T) и g_m(T) неизвестны и поэтому неизвестны абсолютные величины энергий Гиббса. Кроме того, в силу логарифмической зависимости энергии Гиббса от давления (концентрации) нельзя принимать за стандартное состояние газообразных веществ и растворов (в отношении растворенных веществ) бесконечно разреженный газ и бесконечно разбавленный раствор соответственно.

Изменение энергии Гиббса в химической реакции может быть найдено и через абсолютные величины энергий Гиббса компонентов, если бы они были известны:

 

_{(продуктов)} – _{(исходных веществ)}, (2.4)

 

где n_i и n_j – числа молей (коэффициенты в уравнении). Рассмотрим равновесную газовую систему, подставим выражение (2.1) в соотношение (2.4):





 

Первые слагаемые этой суммы являются функцией только температуры и в дальнейшем обозначим их через Ф(Т). С остальными слагаемыми выполним несложные математические преобразования, в результате получаем:

 



 

= Ф(Т) + - =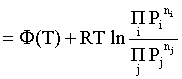

. (2.5)

При равновесии G_{реакции} = 0, с учетом этого для выражения (2.5) получаем: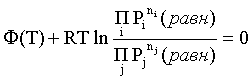

. (2.6)

Логарифм отношения произведений является функцией только температуры: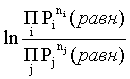

, (2.7)

и пусть он равен ln K_P. Выражение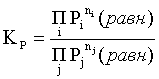

, (2.8)

являющееся константой при данной температуре, называется константой равновесия. Для равновесной смеси реальных газов константа равновесия будет иметь такой же вид, но вместо давлений в ней будут фигурировать фугитивности. Повторяя эти выкладки с выражением для энергии Гиббса компонента раствора (2.3), получаем аналогичное выражение: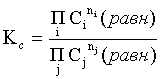

 

. (2.9)

 

В случае реальных растворов концентрации должны быть заменены на активности.

Для газовых равновесий величины К_р и К_с связаны: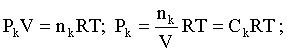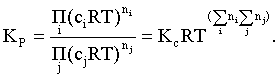



(2.10)

Например, для равновесной системы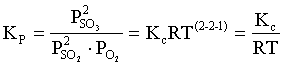

.

Уравнение (2.5) является общим выражением для энергии Гиббса химической реакции. Подставляя в него соотношения (2.7 – 2.9) получаем: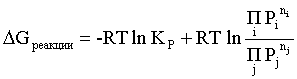

 

(газы);

(2.11)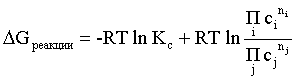

(растворы).

 

При P_i, P_j, c_i и c_j, равных единице (стандартное состояние!) эти соотношения переходят в одно из наиболее употребляемых уравнений термодинамики:

 

. (2.12)

 

Подчеркнем, что в уравнении (2.11) фигурирует термодинамическая константа, она равна К_р или К_с лишь в случае идеального газа или идеального раствора соответственно. Для реальных систем в выражении термодинамической константы равновесия должны быть подставлены величины фугитивностей компонентов газовой смеси или активностей компонентов раствора.

Под знаком логарифма в (2.11) стоят отношения двух величин, выраженных в одних и тех же единицах, – отношение давления к давлению в стандартном состоянии или отношение концентрации к концентрации в стандартном состоянии, то есть безразмерные величины. Таким образом, термодинамическая константа равновесия, стоящая под знаком логарифма в выражении (2.11), является безразмерной величиной. Наконец, отметим, что концентрация индивидуальных жидких и кристаллических веществ постоянна и равна единице и не включается в выражение константы равновесия.

Уравнение (2.12) является одной из основ экспериментального определения стандартных величин энергий Гиббса процессов, в частности – энергий Гиббса образования соединений. Среди других поставщиков термодинамических данных отметим электрохимические измерения. Наконец, подчеркнем, что основным поставщиком термодинамических данных являются калориметрические измерения, позволяющие определять энтальпии и внутренние энергии различных процессов, теплоемкости веществ и систем, что дает возможность определять энтальпии образования соединений и энтропии индивидуальных веществ.

Вернемся теперь к концентрационной и температурной зависимости электродного потенциала. Объединим уравнения (1.20), (1.28) и (2.10) для реального раствора: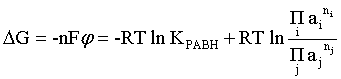

. (2.13)

Отсюда ЭДС электрохимической системы равна: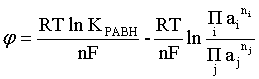

 

(2.14)

При активностях компонентов, равных единице (стандартное состояние!), это уравнение переходит в

 

. (2.15)

 

Сочетая (2.14) и (2.15), получаем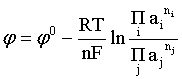

. (2.16)

 

С учетом сказанного в разделе 1.6, соответствующее выражение для электродного потенциала имеет вид: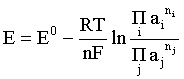

. (2.17)

 

Например, для электродных процессов:

 

Ni²⁺ + 2 ē = Ni; E₁

Fe³⁺ + ē = Fe²⁺; E₂

MnO₄^– + 8H⁺ + 5 ē = Mn²⁺ + 4 H₂O; E₃

 

выражения для электродных потенциалов будут следующими: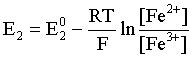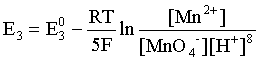

 

;

;

.

 

Обратим внимание, что, меняя концентрации потенциалопределяющих ионов, можно значительно изменять величину, а порой и знак электродного потенциала. Конкретные примеры, иллюстрирующие это, приведены в разделе "Задачи и упражнения" (с. 28).

 

Задачи и упражнения