Конспект лекций. Конспект лекций, задачи и упражнения
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Конспект лекций, задачи и упражнения Допущено Учебно-методическим объединением по образованию в области химической технологии и биотехнологии в качестве учебного пособия для студентов вузов, обучающихся по химико-технологическим направлениям подготовки дипломированных специалистов Москва 2004 ОГЛАВЛЕНИЕ Введение 1. Энергетика процессов 1.1. Внутренняя энергия, энтальпия 1.2. Термохимия, закон Гесса 1.3. Энтропия 1.4. Энергия Гиббса 1.5. Критерий самопроизвольного протекания процессов 1.6. Изменение энергии Гиббса в окислительно-восстановительных реакциях Задачи и упражнения 2. Химическое равновесие 2.1. Истинное и кажущееся равновесие, смещение равновесия 2.2. Количественные характеристики равновесия Задачи и упражнения 3. Некоторые равновесия в растворах 3.1. Образование растворов, растворимость 3.2. Равновесие диссоциации электролитов 3.3. Шкала термодинамических функций образования ионов в водных растворах 3.4. Равновесие растворения и диссоциации малорастворимого электролита 3.5. Равновесие диссоциации воды, буферные растворы 3.6. Гидролиз солей Задачи и упражнения 4. Комплексные соединения 4.1. Общие сведения о комплексных соединениях 4.2. Образование и разрушение комплексных соединений. Диссоциация комплексных соединений Задачи и упражнения 5. Окислительно-восстановительные реакции 6. Эквивалент, закон эквивалентов Задачи и упражнения Приложение Заключение Рекомендуемая литература УДК 546 (075.8) ББК 24.1:24.53 С60 Рецензенты Кандидат химических наук, доцент, заведующий кафедрой неорганической и аналитической химии Московской сельскохозяйственной академии имени К.А. Тимирязева С.Н. Смарыгин Доктор химических наук, профессор, заведующий кафедрой физической химии Российского химико-технологического университета имени Д.И. Менделеева А.В. Вишняков Соловьев С.Н. С 60 Начала химии. Теоретические основы химии. Конспект лекций, задачи и упражнения. М.: РХТУ им. Д.И. Менделеева. 2004. 148 с. ISBN 5-7237-0463-Х В пособии рассматриваются: элементы химической термодинамики; основы учения о равновесии; равновесия в растворах электролитов; комплексные соединения; эквивалент и закон эквивалентов. УДК 546 (075.8) ББК 24.1:24.53 ISBN 5-7237-0463-Х © Российский химико-технологический университет им. Д.И. Менделеева, 2004 © Соловьев С.Н., 2004 ВВЕДЕНИЕ В вузах химического и химико-технологического профиля изучению неорганической химии обычно предшествует дисциплина, где излагаются основные закономерности протекания химических процессов и современные представления о строении вещества. Традиционно в нее включаются элементы химической термодинамики, основы учения о равновесии и рассмотрение ряда важнейших равновесий в водных растворах, общие сведения о протекании химических реакций; элементы теории строения молекул и химической связи, представления о межмолекулярном взаимодействии, теория химической связи в комплексных соединениях и общая информация об этих соединениях. Данное пособие представляет собой первую часть сжатого конспекта лекций по теоретическим основам химии, оно содержит большое число разобранных задач и заданий, закрепляющих усвоение основного лекционного материала и дающих практические навыки его использования. Такое сочетание лекционного и семинарского материала позволяет самостоятельно изучать необходимые разделы курса, готовиться к зачетам и экзаменам. В пособие включен материал по следующим разделам курса: элементы химической термодинамики, учение о равновесии, равновесия в растворах, окислительно-восстановительные реакции, комплексные соединения, эквиваленты и закон эквивалентов. Пособие будет полезно студентам медицинских, химических и технологических вузов, старшеклассникам, занимающимся углубленным изучением химии, и их педагогам. 1. ЭНЕРГЕТИКА ПРОЦЕССОВ 1.1. Внутренняя энергия, энтальпия Химическая термодинамика, элементы которой используются в общехимических курсах, оперирует так называемыми характеристическими функциями или функциями состояния, позволяющими через значения самих функций и их производных определить любое термодинамическое свойство. Познакомимся с некоторыми из них. Системой в термодинамике называют тело (вещество, несколько веществ) или группу взаимодействующих тел, мысленно выделяемых, обособляемых от окружающей среды. Примеры систем: Земля, колонна синтеза аммиака, пробирка с реактивами. Система, имеющая постоянный объем и рассматриваемая как необменивающаяся веществом и энергией с окружающей средой, называется изолированной. Создать действительно изолированную систему практически невозможно. Движение представляет собой неотъемлемое свойство материального мира, мерой движения является энергия. Теплота и работа представляют собой виды энергии. В первом случае (теплота) энергия передается путем хаотического столкновения молекул на границе соприкасающихся тел. Работа качественно разнообразна (работа в поле тяготения, работа электрического поля, работа расширения и т.д.), отражая различные виды взаимодействия, и характеризуется перемещением большого числа частиц. Закон сохранения энергии (или первый закон термодинамики) утверждает: теплота Q, поведенная к системе, расходуется на совершение системой работы A и на изменение ее внутренней энергии U: Q = U + A. (1.1) Внутренняя энергия представляет собой однозначную, конечную и непрерывную (а значит, и дифференцируемую!) функцию состояния, аргументами которой являются температура, давление, природа и число молей вещества и т.д. Как дифференцируемая функция внутренняя энергия обладает свойством независимости ее изменения при переходе от начального состояния (1) к конечному (2) от пути перехода: U=U2 – U1. (1.2) А вот теплота в общем случае не является дифференцируемой функцией. Внутренняя энергия системы подразумевает общий ее запас, включая энергию поступательного и вращательного движения молекул, внутримолекулярную энергию электронов, внутриядерную энергию и т.д. Фактически абсолютная ее величина зависит от уровня наших знаний о различных видах энергии, а также о фундаментальных частицах и характере их взаимодействия. Поэтому до тех пор пока не решена проблема существования последней фундаментальной частицы, сама проблема определения абсолютного значения внутренней энергии лишена смысла. Обычно работу разделяют на полезную и работу расширения: А = Апол + Арасш . (1.3) Работа расширения может быть найдена следующим образом: , (1.4) где Р - давление, V - объем. Для изобарного процесса (P=const) уравнение (1.4) принимает вид: 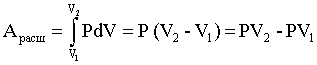 . (1.5) . (1.5)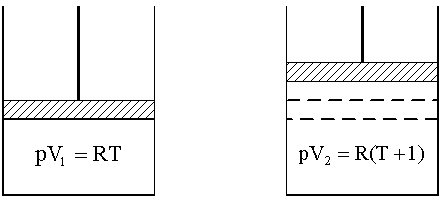 Рис. 1. К пояснению физического смысла газовой постоянной Отметим, что любая химическая система, в которой происходит изменение объема, будет характеризоваться работой расширения. В связи с обсуждением этой величины обратимся к физическому смыслу универсальной газовой постоянной R. Рассмотрим систему, содержащую 1 моль идеального газа, находящегося при постоянном давлении в цилиндре под невесомым поршнем, двигающемся без трения. Систему нагрели на 1 K, газ расширился, поршень поднялся, совершена работа расширения (рис.1). Состояния газа описываются уравнением Менделеева-Клапейрона для начального состояния системы PV1 = RТ и для конечного состояния PV2 = R (Т+1). Работа расширения согласно (1.4) и (1.5) составит: Арасш = PV = PV2 – PV1 = R (T+1) – RT = R. Таким образом, численное значение универсальной газовой постоянной равно работе расширения 1 моль идеального газа, находящегося при постоянном давлении, при нагревании на 1 К. Рассмотрим систему при постоянном давлении, для которой отсутствует полезная работа (Апол = 0). Согласно соотношениям (1.1) и (1.5): QP=U+Aрасш = U+PV=U2–U1+PV2–PV1=U2+PV2–(U1+PV1). (1.6) Вводим новую термодинамическую функцию, называемую энтальпией, которая определяется соотношением: H = U+РV . (1.7) Соответственно выражение (1.6) приобретает вид: QP=H2–H1=H. (1.8) Как видно из определения, энтальпия будет обладать свойством независимости ее изменения при переходе от начального состояния к конечному от пути перехода; она является однозначной, конечной и непрерывной функцией состояния. Абсолютные значения энтальпий, как и абсолютные значения величин внутренней энергии, неизвестны. Поэтому в учебной и научной литературе слово "изменение" в выражениях типа "изменение энтальпии (внутренней энергии) в процессе" опускают и говорят об "энтальпии (внутренней энергии) процесса", понимая под этим величины H и U. Подчеркнем, что изобарный режим (в основном Р=1 атм) является наиболее распространенным для лабораторной и промышленной реализации различных процессов. 1.2. Термохимия, закон Гесса Раздел химии, в котором изучают тепловые эффекты химических реакций, называется термохимией. Термохимия оперирует так называемыми термохимическими уравнениями, представляющими собой обычные химические уравнения, в которых указана величина сопровождающего реакцию теплового эффекта и термодинамическое состояние каждого из участников. Под последним понимают температуру, агрегатное состояние участников, состав и концентрации растворов. Термодинамика использует так называемую эгоистическую систему знаков величин тепловых эффектов: экзотермическим процессам, идущим с тепловыделением, соответствуют отрицательные величины энтальпий. Наоборот, эндотермическим процессам соответствуют положительные значения величин H и U. Примеры термохимических уравнений процессов: N2 (г) + 3H2 (г)= 2NH3 (г); H298 = – 92 кДж; NaOH (р-р NaOH 100 H2O) + HCl (р-р HCl 100 H2O) = = NaCl (р-р NaCl 201 H2O) + H2O (ж); H298 = – 57 кДж Нижний подстрочный индекс у величин H указывает температуру, к которой отнесен тепловой эффект. Рассмотрим систему, в которой отсутствует полезная работа. Тогда, согласно (1.1) и (1.4) при постоянном объеме: QV=U, а при постоянном давлении согласно (1.8): QP=H. Иными словами, в этих двух случаях тепловой эффект процесса не зависит от пути перехода от исходных веществ к продуктам реакции. Эта закономерность и представляет собой основной закон термохимии, установленный чисто экспериментально в 1840 г. нашим соотечественником Г.И. Гессом: энтальпия (внутренняя энергия) химической реакции не зависит от пути перехода от начальных веществ к продуктам реакции, а определяется только видом и состоянием этих исходных веществ и продуктов. Закон Гесса позволяет производить с термохимическими уравнениями алгебраические операции: складывать, вычитать, умножать и делить на постоянное число. Проиллюстрируем это на простом примере. Пусть известны энтальпии следующих процессов: 1) N2 (г) + O2 (г) = NO (г); H1 = 90,2 кДж; 2) NO (г) + O2 (г) = NO2 (г); H2 = – 56,8 кДж; Необходимо найти энтальпию процесса: 3) N2 (г) + O2 (г) = NO2 (г); H3 . Как видно, искомое термохимическое уравнение получается сложением первого и второго термохимических уравнений, соответственно: H3=H1+H2=90,2+(–56,8)=33,4 кДж. Различным типам физических и химических процессов соответствуют различные величины энтальпий: К(к) = К(ж); Hплавл H2O (ж) = H2O (г); Hиспар NaOH (р-р) + HBr (р-р) = NaBr (р-р) + H2O (ж); Hнейтр . Наиболее важны энтальпии образования и энтальпии сгорания. Под энтальпией образования вещества понимают энтальпию процесса образования 1 моль этого вещества из простых веществ при данной температуре. При этом совершенно безразлично – осуществим этот процесс или нет. Примеры (Т=298,15 К): Ca (к) + C (к,графит) + O2 (г) = CaCO3 (к); H=Hобр CaCO3 (к); N2(г)+2Cr(к)+4H2(г)+O2(г) = (NH4)2Cr2O7 (к); H=Hобр(NH4)2Cr2O7(к). Отметим, что при наличии у простого вещества аллотропных модификаций в термохимических уравнениях для энтальпий образования используется наиболее устойчивая из них. При 298,15 К из аллотропных модификаций углерода таковой является графит, у олова – олово белое, у серы – сера ромбическая т. д. Единственное исключение – фосфор, для которого в качестве простого вещества взят не более устойчивый красный фосфор, а более реакционноспособный белый фосфор. Под энтальпией сгорания вещества понимают энтальпию сгорания 1 моль этого вещества при данной температуре с образованием CO2(г) и H2O(ж), состав остальных веществ указывают специально, например: (CH3)2S(г)+O2(г) = 2CO2(г)+3H2O(ж)+S(к); H=Hсгор(СH3)2S до S (CH3)2S(г)+O2(г) = 2CO2(г)+3H2O(ж)+SO2 (г); H=Hсгор(СH3)2S до SO2 . Особое значение имеют стандартные величины; они относятся к процессам, где все участники находятся в так называемых стандартных состояниях. За стандартное состояние индивидуальных жидких и кристаллических веществ принимается их реальное состояние при данной температуре и давлении 1 атм (101325 Па). Определения стандартных состояний для газов и растворов связаны с понятиями "идеальный газ" и "идеальный раствор". Как известно, состояние всех идеальных газов (и части реальных газов при низких давлениях) описывается уравнением Менделеева-Клапейрона: PV=nRТ, (1.9) где n - число молей газа. Уравнения же состояния реальных газов сложны, громоздки и практически индивидуальны для каждого газа. С целью сохранить простую и единообразную форму описания всех реальных газовых систем поступают следующим образом. Вводится функция, называемая фугитивностью f или летучестью, рассматриваемая как исправленное давление, и все проблемы отклонений свойств реальных газов от свойств идеальных газов сводятся к нахождению этой величины. Другими словами фугитивностью называют такую величину, которая связана с другими термодинамическими характеристиками реального газа так же, как с ними связано давление в случае идеального газа. Таким образом, уравнения состояния: для идеального газа PV=nRT; для реального газа fV=nRT Совершенно аналогичная ситуация с идеальными и реальными растворами. Напомним, что модели идеального газа и идеального раствора идентичны, что отражается термином "идеальный раствор газов". Активностью называют такую величину, которая связана с другими термодинамическими характеристиками реальных растворов так же, как с ними связана концентрация в случае идеальных растворов. Активность а связана с концентрацией с через коэффициент активности . Именно последний и отражает степень отклонения свойств реального раствора от свойств идеального раствора, его численное значение зависит от способа выражения концентрации. Обратимся теперь к определениям стандартных состояний для газов и растворов. За стандартное состояние газообразных веществ принимают гипотетический идеальный газ, фугитивность которого равна единице, а энтальпия – энтальпии реального газа при давлении, стремящемся к нулю. За стандартное состояние раствора (в отношении растворенного вещества) принимают гипотетический идеальный раствор, активность растворенного вещества в котором равна единице, а энтальпия – энтальпии растворенного вещества в реальном бесконечно разбавленном растворе. Если же раствор рассматривается как единая система, то используется данное выше определение стандартного состояния для индивидуальной жидкости. Отметим, что в отношении только энтальпийных характеристик определения стандартных состояний газов и растворов сравнительно просты – за стандартное состояние принимается реальный бесконечно разреженный газ или реальный бесконечно разбавленный раствор, соответственно. Величины стандартных энтальпий образования обычно при 298,15К табулированы (некоторые величины приведены в табл. 1 приложения) и в первую очередь используются при расчетах стандартных энтальпий процессов. Основанием для этого является первое следствие из закона Гесса: Hреакции = (продуктов) – (исходных веществ), (1.11) где ni и nj – числа молей (коэффициенты в уравнении). Для этой же цели можно воспользоваться и вторым следствием из закона Гесса: Hреакции = (исходных веществ) – (продуктов). (1.12) Проиллюстрируем эти закономерности на примере реакции: 3C2H2 (г) = C6H6 (ж); . Реакции образования:
Искомая реакция получается сложением первой реакции со второй, умноженной на (-3), соответственно: = – 3 = С6H6 (ж) – 3С2H2 (г) . Реакции сгорания:
Искомая реакция получается вычитанием первой реакции из утроенной второй реакции, соответственно: = 3 – = 3С2H2 (г) – С6H6 (ж). Наконец, назовем третье следствие из закона Гесса: H прямого процесса = - H обратного процесса Рассмотрим некоторые примеры использования закона Гесса. а) Энтальпия образования кристаллогидрата из безводной соли и воды. Пусть требуется определить энтальпию следующего процесса: А(к) + n H2O (ж) = An H2O (к);. Экспериментально осуществить этот процесс и измерить его тепловой эффект практически невозможно. При этом сравнительно легко измерить энтальпии следующих процессов: 1) А(к) + Х H2O (ж) = A(р-р, АХ H2O);; 2) АnH2O (к) + (X-n) H2O (ж) = A(р-р, АХ H2O);. Как видно, искомое уравнение получается вычитанием второго уравнения из первого, соответственно: HX = H1 - H2 . Можно представить рассматриваемые процессы в виде следующей схемы: 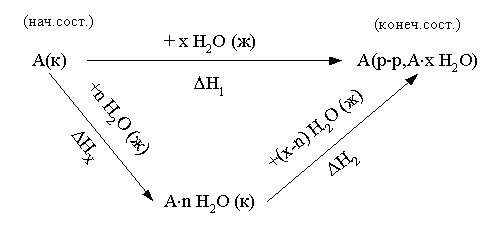 По закону Гесса энтальпия перехода из начального состояния к конечному не зависит от пути перехода, то есть H1=HX+H2 . б) Энтальпия связи. Под энтальпией (энергией) связи А–В в молекуле АВ понимают энтальпию (энергию) разрыва 1 моль названных связей, при этом атомы разводятся на бесконечно большое расстояние. Понятно, что разорвать связи на атомы возможно только в газовой фазе. Например: HCl (г) = H (г) + Cl (г); H0=H0связи H-Cl . Под средней энтальпией связи А–В в молекуле АВn, понимают часть энтальпии разрыва всех связей в 1 моль молекул АВn до состояния атомов, атомы разводятся на бесконечно большое расстояние. Например: NH3 (г) = N (г) + 3H (г); H0=3H0ср.связи N-H . Энтальпии связей могут быть найдены на основе первого следствия из закона Гесса по величинам энтальпий образования атомов и молекул; возможно и комбинирование термохимических уравнений. Например, требуется определить энтальпию связи в молекуле NO на основе данных по энтальпиям связей в молекулах N2 и О2, а также энтальпии образования NO. Запишем все исходные данные соответствующими термохимическими уравнениями: 1) N2 (г) = 2N (г); ; 2) O2 (г) = 2O (г); ; 3) O2 (г) +N2 (г) = NO (г); г . Термохимическое уравнение искомого процесса: NO (г)=N (г)+O (г); может быть получено вычитанием третьего уравнения из полусуммы первого и второго уравнений. Соответственно: 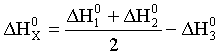 . .Отметим, что комбинирование термохимических уравнений собственно и привело к расчету, основанному на первом следствии из закона Гесса. 1.3 Энтропия Один из важнейших вопросов для химика, на который термодинамика дает ответ, – возможность и условия протекания химических реакций. Самопроизвольными называют процессы, протекающие самопроизвольно, то есть без привлечения работы извне. А вот в результате осуществления таких процессов как раз и может быть выполнена работа против внешних сил. Примеры самопроизвольных процессов: переход теплоты от горячего тела к холодному, реакция нейтрализации, взрыв смеси водорода с кислородом. Несамопроизвольными называют процессы, для протекания которых необходима затрата работы извне. Примеры несамопроизвольных процессов: переход теплоты от холодного тела к горячему, распад воды на водород и кислород при комнатной температуре. Термодинамика оперирует так называемыми равновесными процессами, проходящими через одни и те же состояния, бесконечно близкие к равновесию. Такие процессы являются идеальными, гипотетическими. Реальные, то есть самопроизвольные процессы, в той или иной степени неравновесны. Под химически обратимыми понимают реакции, которые могут идти в прямом и обратном направлениях. Термодинамически обратимыми называют равновесные процессы, протекающие в прямом, а затем – обратном направлениях так, что не только система, но и окружающая среда возвращаются в исходное состояние. Это без сомнения идеальные (абстрактные) процессы. Познакомимся еще с одной термодинамической функцией – энтропией S. Ее изменение для обратимого изотермического перехода теплоты от системы к системе составляет: S=S2–S1= или S=. (1.13) Это соотношение фактически выражает второй закон термодинамики. Для неравновесных (реальных, самопроизвольных) переходов изменение энтропии равно: S=(S2–S1)>. (1.14) Объединяя эти соотношения, получим: . (1.15) В этом выражении знак равенства относится к обратимым (гипотетическим, нереальным) процессам, а знак неравенства – к реальным (самопроизвольным) процессам. Энтропия, аналогично энтальпии и внутренней энергии, является однозначной, конечной и непрерывной функцией состояния. Она зависит от природы вещества, агрегатного состояния, температуры, давления. Эта термодинамическая функция чрезвычайно чувствительна к внутреннему устройству системы, степени ее упорядоченности. Наблюдаемое (макроскопическое) состояние системы может существовать при различных распределениях молекул (частиц) по скоростям и координатам, то есть реализуется различными микросостояниями. Число таких микросостояний, которыми реализуется данное макросостояние, называется термодинамической вероятностью W. В отличие от математической вероятности, принимающей значения от нуля до единицы, термодинамическая вероятность – огромное число. Энтропия 1 моль вещества связана с термодинамической вероятностью следующим соотношением: S=RlnW. (1.16) По мере понижения температуры число распределений частиц системы по координатам и скоростям уменьшается, то есть уменьшается W. В пределе при 0 К частицы (молекулы) "застынут" и данное макросостояние будет реализовано одним единственным распределением частиц по координатам и скоростям, иными словами термодинамическая вероятность будет равна единице, следовательно согласно соотношению (1.16) энтропия будет равна нулю: T 0 K; W 1; S 0. (1.17) Соотношение (1.17) выражает суть третьего закона термодинамики, согласно которому при 0 К энтропия правильно образованного кристалла любого простого вещества или соединения в чистом состоянии равна нулю. Этот закон открывает путь для определения абсолютных величин энтропии. Если вещество находится в стандартном состоянии, то оно характеризуется стандартной энтропией. Величины стандартных энтропии некоторых веществ и ионов при 298,15 К приведены в табл. 1 приложения. Отметим, что энтропия газа гораздо больше энтропии жидкости, которая в свою очередь больше энтропии кристалла (рис. 2). Это позволяет проводить оценку знака величины S процесса, которая рассчитывается согласно соотношению: Sреакции = (продуктов) - (исходных веществ). 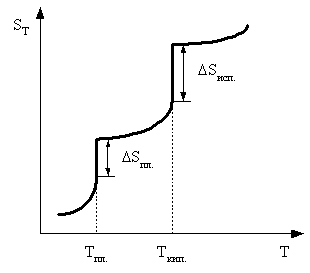 Рис. 2. Температурная зависимость энтропии Какую же общую полезную информацию дает энтропия для химика? 1. Энтропия характеризует степень упорядоченности в системе, в данном конкретном веществе. Чем ниже S, тем меньше W, тем более компактно вещество, имеет большую твердость, плотность; кристаллические вещества характеризуются меньшей энтропией, чем аморфные вещества, энтропия возрастает с увеличением атомной и молярной масс. 2. Соотношение (1.15) для изолированной системы (Q=0) принимает вид: S 0. (1.18) Соотношение (1.18) означает, что для изолированной системы, в которой протекают обратимые процессы, энтропия постоянна (S=0) и возрастает (S>0) в необратимом (реальном, самопроизвольном) процессе. Таким образом, получаем критерий самопроизвольного протекания процессов в изолированной системе – самопроизвольно идут процессы, приводящие к росту энтропии. Очевидно, самопроизвольное течение процесса будет возможно до тех пор, пока энтропия не достигнет максимального значения. Указанный критерий весьма ограниченный, так как изолированные системы крайне редки. Познакомимся с более общим критерием, и предварительно введем еще одну термодинамическую функцию. 1.4. Энергия Гиббса Рассмотрим систему, находящуюся при постоянных температуре и давлении. Объединим вместе соотношения (1.1), (1.3), (1.5) и (1.15): TS U + PV + Aпол . (1.19) Выражаем величину Апол через термодинамические функции: –Апол U + PV – TS = U2–U1 + P(V2–V1) – T (S2–S1)= =U2+PV2–TS2–(U1+PV1–TS1). (1.20) Вводим новую термодинамическую функцию, называемую энергией Гиббса: G U + PV – TS = H – TS. (1.21) Из определения этой функции следует, что абсолютное ее значение, как и функций Н и U, неизвестно, изменение этой функции при переходе от начального состояния к конечному не зависит от пути перехода. Аналогично введенным выше величинам энтальпий образования, энтальпий сгорания, стандартных энтальпий процессов вводим величины энергий Гиббса образования, энергий Гиббса сгорания, стандартных энергий Гиббса процессов. По следствию из закона Гесса энергия Гиббса химической реакции может быть найдена: Gреакции = (продуктов) - (исходных веществ), (1.22) где ni, nj – числа молей (коэффициенты в уравнении). Величины стандартных энергий Гиббса образования веществ обычно при 298,15 К табулированы (некоторые значения представлены в табл. 1 приложения). Физический смысл энергии Гиббса вытекает из соотношения (1.20) –энергия Гиббса в равновесном процессе с точностью до знака равна полезной работе, которую может совершить система. В случае протекания неравновесных процессов энергия Гиббса будет (с обратным знаком) равна максимально возможной полезной работе, которую может совершить система. 1.5. Критерий самопроизвольного протекания процессов При постоянных температуре и давлении, как уже говорилось выше, из соотношения (1.20) следует: G–Aпол . (1.23) При отсутствии полезной работы получаем: G0. (1.24) Из этого соотношения следует, что при протекании обратимых химических реакций энергия Гиббса неизменна (G=0), а при протекании реальных, самопроизвольных процессов она уменьшается. Иными словами, получаем общий критерий (при постоянных температуре и давлении) самопроизвольного протекания процесса: при P=const, T=const самопроизвольно протекают только процессы, сопровождающиеся уменьшением энергии Гиббса. Пределом протекания процесса будет состояние с минимальным при данных условиях значением энергии Гиббса. После достижения минимума энергия Гиббса перестает изменяться и G=0, система находится в состоянии равновесия. Например, взрыв смеси водорода и кислорода – H2 (г) + O2 (г) = H2O (ж); =–237 кДж – самопроизвольный процесс: достаточно внести в эту смесь спичку или катализатор и мгновенно начинается реакция. Обратный процесс – разложение воды при 298,15 К на водород и кислород – имеет значение энергии Гиббса 237 кДж/моль. Это несамопроизвольный процесс, для его реализации необходимо привлечение работы извне, например, работы электрического тока. Таким образом, приходим к выводу, что критерием невозможности самопроизвольного протекания процесса будет положительное значение энергии Гиббса этого процесса. Подчеркнем, что высказанный критерий самопроизвольного протекания процесса имеет принципиальный характер, он является необходимым условием для самопроизвольного протекания процесса. Достаточные же условия составляют область химической кинетики. Сказанное можно иллюстрировать следующей схемой: 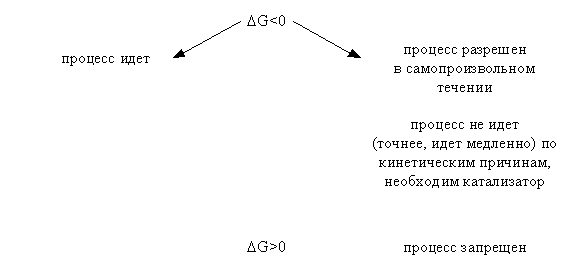 Из соотношения (1.21) следует, что G = H – TS. (1.25) Поэтому при анализе вопроса о возможности самопроизвольного протекания процесса необходимо рассматривать два вклада (H и TS) или, как говорят, энтальпийный и энтропийный факторы. Самопроизвольное течение процесса возможно при:
Энергия Гиббса является мерой химического сродства, чем отрицательнее G химической реакции, тем проще, в более мягких условиях идет процесс. В интервалах температур порядка сотен Кельвинов температурная зависимость величин H и S невелика и ею можно пренебречь. Иными словами, точное соотношение GT=HT–TST заменяется приближенным GTH298–TS298 . (1.26) Это выражение позволяет оценивать значения энергии Гиббса при температурах, отличных от 298,15 К. Например, необходимо оценить условия, при которых самопроизвольно протекает реакция: СаСО3 (к) = СаO (к) + СO2 (г) . Характеристики этой реакции при 298,15 К: G0298=G0обр.CO2 (г)+ G0обр.CaO (к)–G0обр.CaCO3 (к) =130,6 кДж; H0298=H0обр.CO2 (г)+ H0обр.CaO (к)–H0обр.CaCO3 (к) =178,4 кДж; S0298=S0CO2 (г) + S0CaO (к)–S0CaCO3 (к) = 160,5 Дж/К. При 298,15 К данная реакция самопроизвольно не протекает (), энтальпия и энтропия реакции также положительны. А это означает, что с ростом температуры отрицательный энтропийный вклад будет расти и после достижения определенной температуры превысит положительный энтальпийный вклад. Границей перехода от запрещенного процесса к самопроизвольному протеканию является GT=0. Тогда, согласно соотношению (1.25) получаем: ; 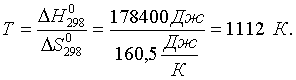 Таким образом, при температурах выше 8390С разложение карбоната кальция станет самопроизвольным процессом. 1.6. Изменение энергии Гиббса в окислительно-восстановительных реакциях Традиционно химические реакции делят на обменные и окислительно-восстановительные. Под последними понимают реакции, в которых происходит изменение степеней окисления атомов в молекулах реагирующих веществ. Для подобных процессов критерий самопроизвольного протекания может быть выражен через так называемые величины электродных потенциалов. Рассмотрим систему, состоящую из металлического электрода, например медного, погруженного в раствор соли этого металла. Концентрация ионов Cu2+ в металле при данных условиях постоянна, концентрация же этих ионов в растворе определяется концентрацией соли. В зависимости от последней на границе металл-раствор начинается либо переход ионов Cu2+ в раствор, либо осаждение этих ионов на поверхности электрода. Так или иначе, поверхность металла становится заряженной, для компенсации этого заряда из раствора подойдут к поверхности металла ионы противоположного знака. На границе металл-раствор возникает так называемый двойной электрический слой, характеризующийся соответствующим скачком потенциала. Экспериментально измерить его величину невозможно. Поскольку измерению поддается лишь величина электродвижущей силы (ЭДС) электрохимической цепи, то опытным путем можно определить только относительные величины так называемых электродных потенциалов, ЭДС цепи, составленной из данного электрода и некоторого стандартного электрода, потенциал которого условно принимают равным нулю. В качестве стандартного электрода или электрода сравнения принят обратимый водородный электрод, в котором газообразный водород находится при давлении 1 атм и насыщает платиновый электрод. Раствор, в который помещен водородный электрод, содержит ионы водорода с активностью, равной единице. Таким образом, электродным потенциалом Е данного электрода называют ЭДС элемента, составленного из этого электрода и водородного электрода. Например, для нахождения электродного потенциала меди надо составить следующий электрохимический элемент: (-) Pt, H2 | H+,aq | Cu2+,aq | Cu(+). Понятно, что для записи уравнений электродных полуреакций и введения соответствующей системы знаков величин электродных потенциалов возможны два подхода. Наиболее распространен вариант, где электродные полуреакции записывают в окислительной форме, а система знаков такова, что написанному медному электроду соответствует (в стандартных условиях) положительное значение электродного потенциала. В этой системе знаков значение ЭДС () процесса будет находиться по соотношению: = Еокисл – Евосст. (1.27) Гораздо более многочисленны электроды, реакции на которых не связаны с выделением веществ из раствора или растворением материала электрода. Перенос электронов в таких реакциях связан с изменением зарядов ионов в растворе. Примером такого электрода является электрод, состоящий из платиновой пластины, опущенной в раствор, содержащий соли железа (II) и (III). Платина индифферентна к указанным соединениям и служит лишь переносчиком электронов: Платиновый электрод получает положительный заряд и притягивает анионы из раствора; на поверхности электрода образуется двойной электрический слой и возникает соответствующий скачок потенциала. Его величина (при постоянных температуре и давлении) зависит только от концентраций солей железа (I1) и (III) в растворе. Знак потенциала и его величина определяются относительно водородного электрода. Некоторые величины стандартных электродных потенциалов при 298,15 К приведены в табл. 2 приложения. Полезная работа Апол электрохимического элемента представляет собой работу электрического тока и может быть найдена: Аэлек = q = nF, (1.28) где q - количество электричества, n – число электронов, отдаваемых или присоединяемых в элементарном акте, F – число Фарадея. Согласно (1.20) для обратимых процессов G= –Апол = –nF. Самопроизвольному течению процесса соответствует отрицательное значение энергии Гиббса, следовательно, для реакций, протекающих в электрохимических элементах (окислительно-восстановительных реакций) должно выполняться: –nF < 0. Поскольку n и F положительны, то приходим к заключению, что самопроизвольно протекают те окислительно-восстановительные реакции, для которых величины ЭДС положительны. Например, определим, возможно ли в стандартных условиях окисление перманганатом калия ионов Fe2+ и Co2+ до Fe3+ и Со3+ в кислой среде. Величины электродных потенциалов: MnO4– + 8H+ + 5ē = Mn2+ + 4H2O; =1,51 В (окисл); Fe3+ + ē = Fe2+; =0,77 В (восст); Co3+ + ē = Co2+; =1,82 В (восст). Для первого процесса == 1,51–0,77 = 0,74 В. Для второго процесса == 1,51–1,82 = –0,31 В. Как видно, самопроизвольное течение возможно лишь для первого процесса. Вторая реакция запрещена, перманганат-ион не может окислить ион Co2+ до Co3+, а наоборот - в кислой среде ион Co3+ окисляет Mn2+ до перманганат-иона. Зависимость величины электродного потенциала от температуры и концентраций реагирующих веществ будет приведена ниже. Задачи и упражнения | ||||||||||||
