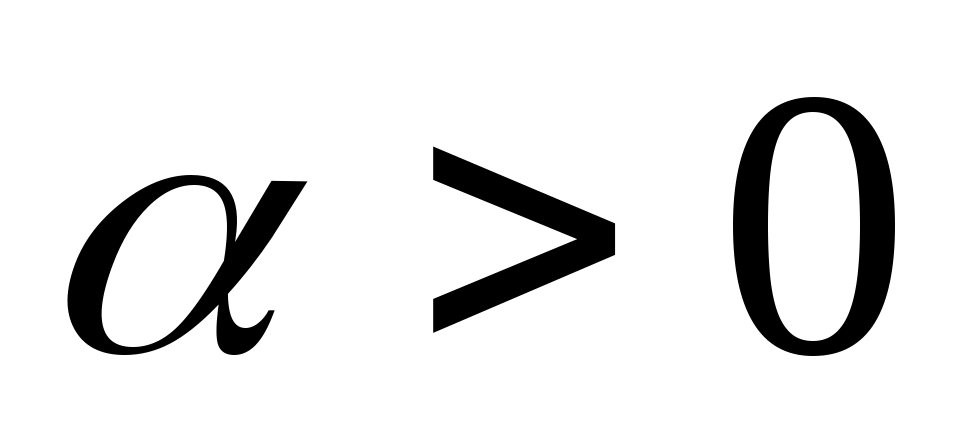 , ,  . Найти корреляционную функцию, дисперсию и эффективную ширину спектра процесса . Найти корреляционную функцию, дисперсию и эффективную ширину спектра процесса 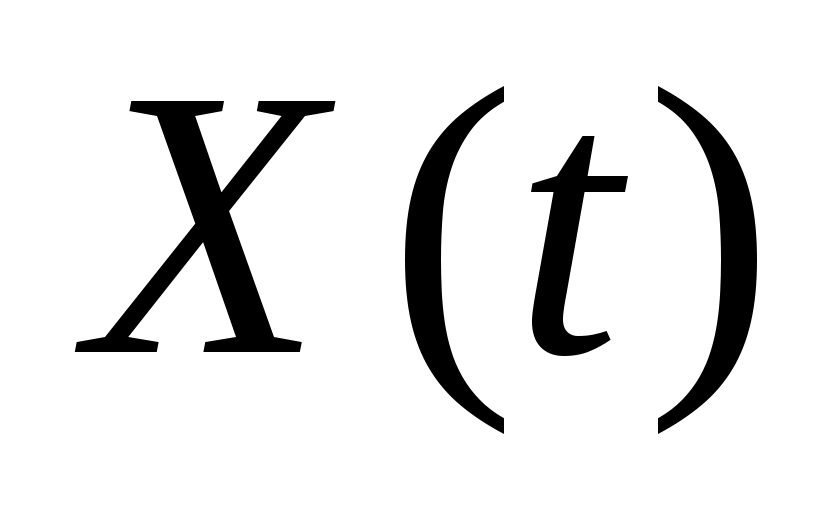 . .
К онтрольная работа № 1 онтрольная работа № 1
по дисциплине «Анализ случайных процессов»
Вариант № 10
1. Рассматривается случайная функция 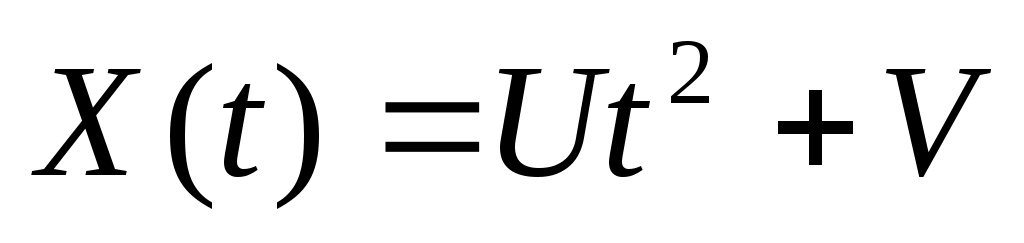 , где , где 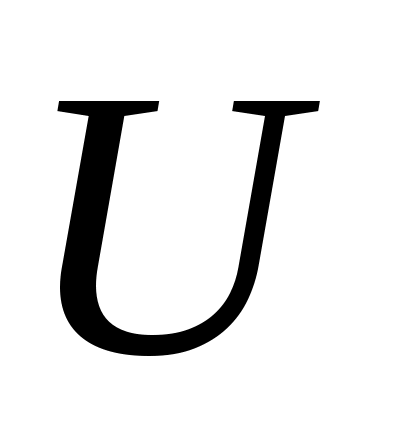 , , 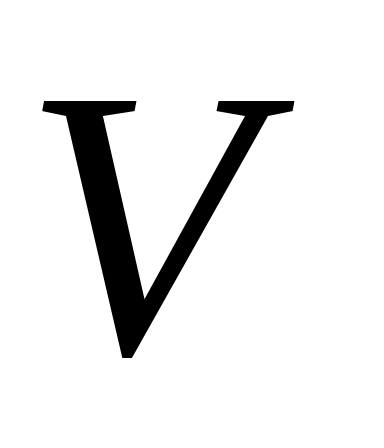 – некоррелированные случайные величины, распределенные по нормальным законам – некоррелированные случайные величины, распределенные по нормальным законам 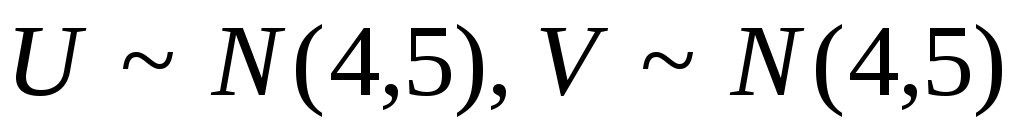 . Найти плотность распределения сечения этой функции и характеристики . Найти плотность распределения сечения этой функции и характеристики 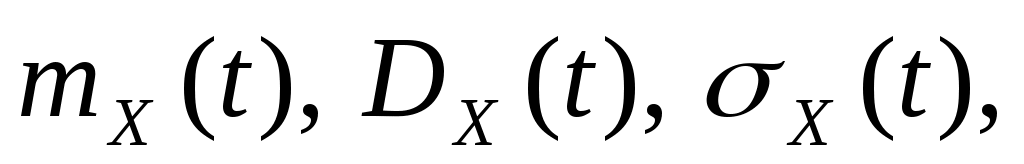 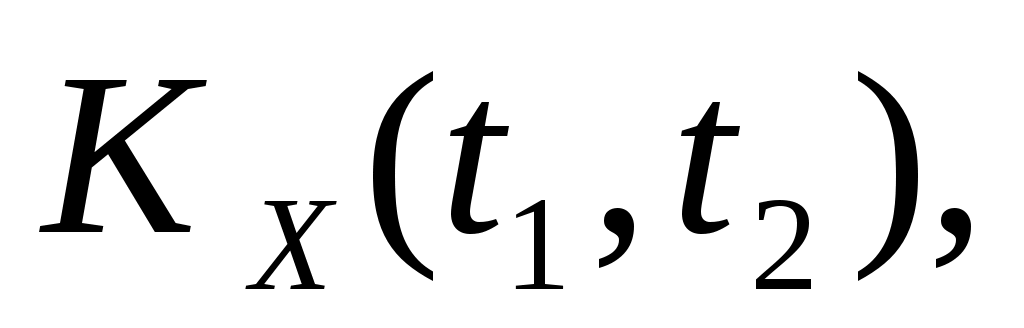 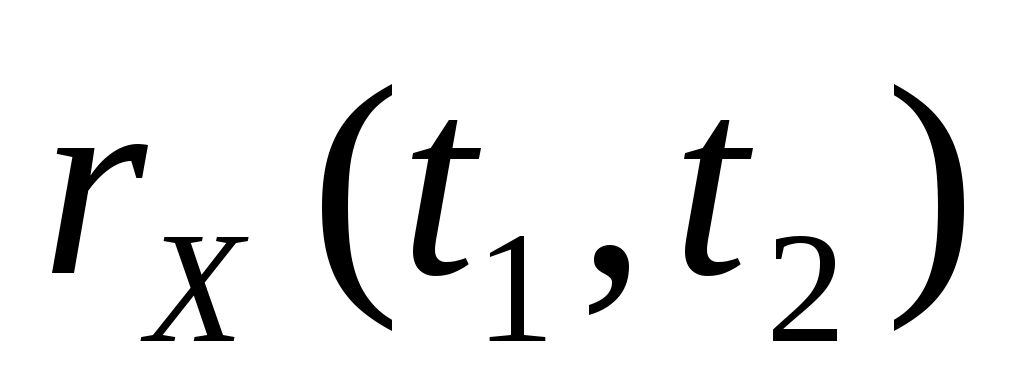 . .
2. Случайная функция 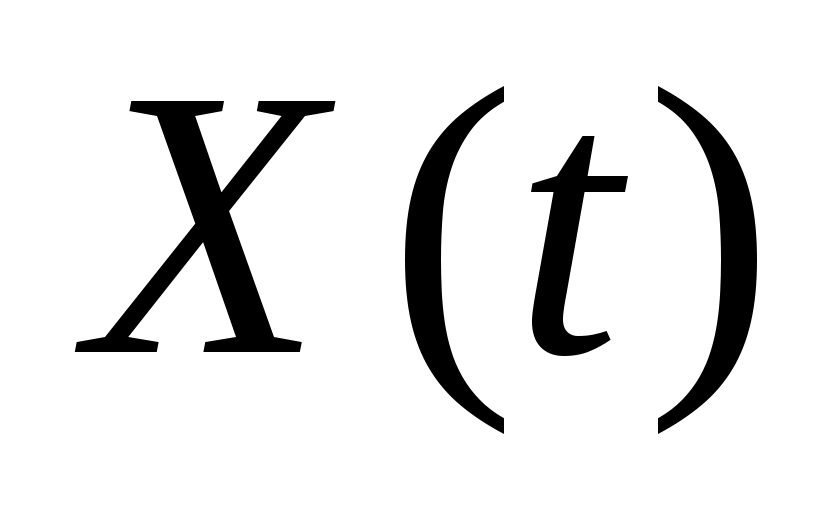 задана своим каноническим разложением задана своим каноническим разложением 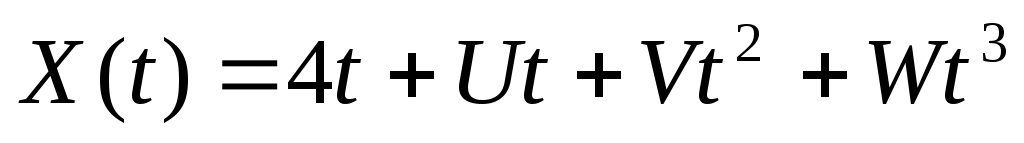 , где , где 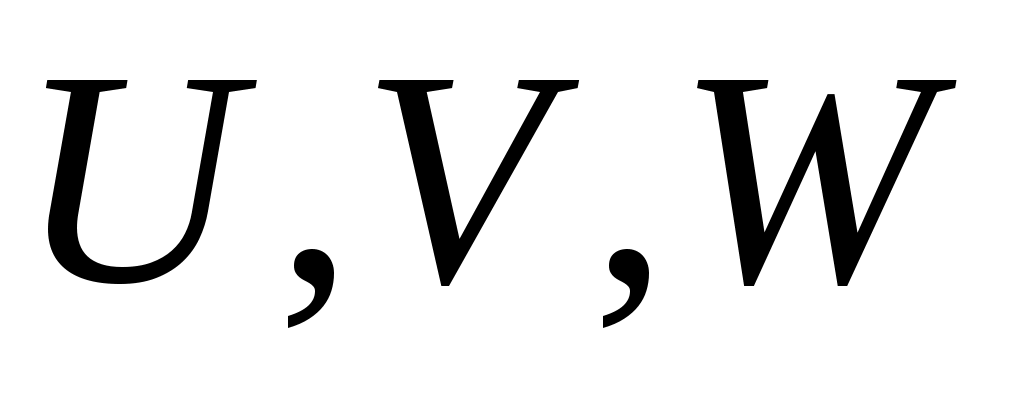 – некоррелированные случайные величины с м.о., равными нулю, и дисперсиями – некоррелированные случайные величины с м.о., равными нулю, и дисперсиями 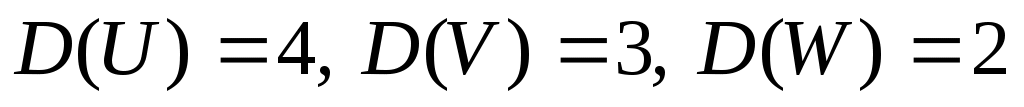 . Найти характеристики случайной функции . Найти характеристики случайной функции 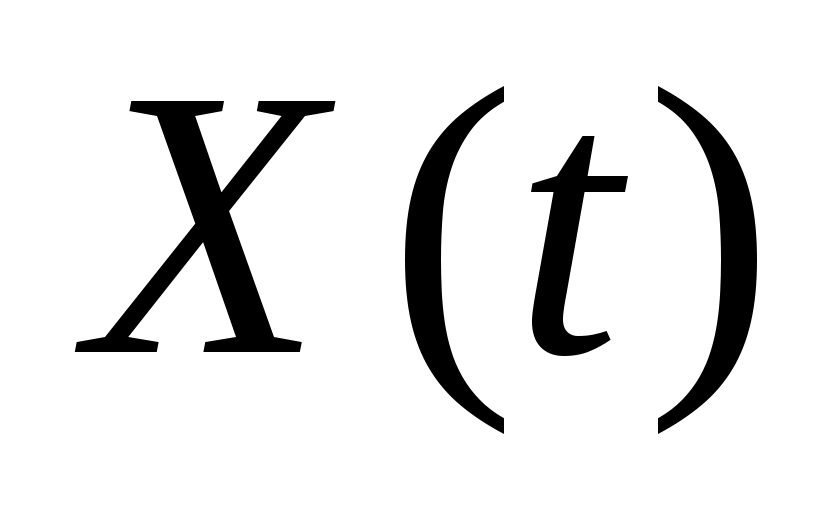 : : 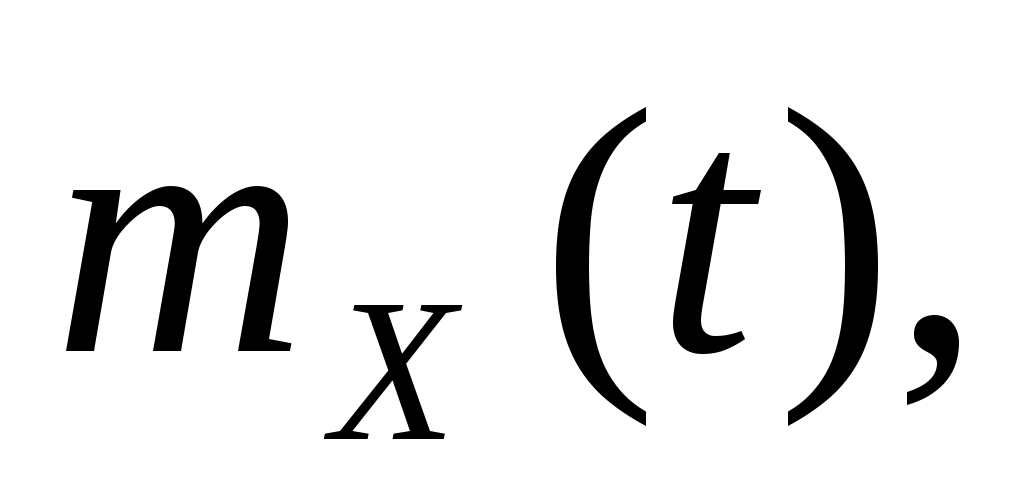 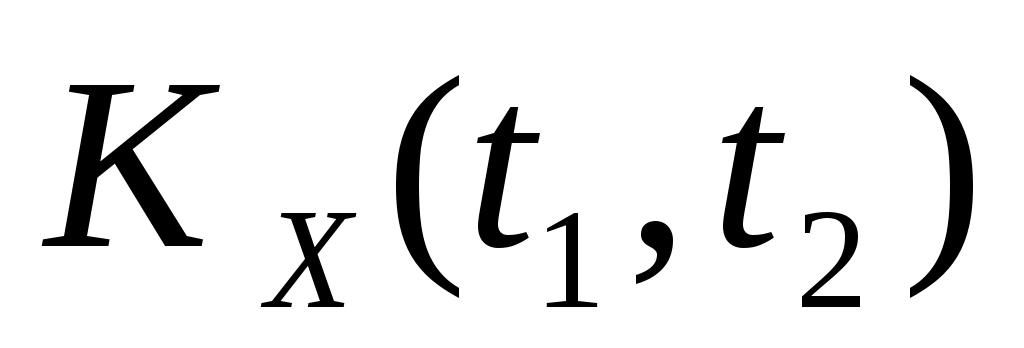 , а также случайной функции , а также случайной функции 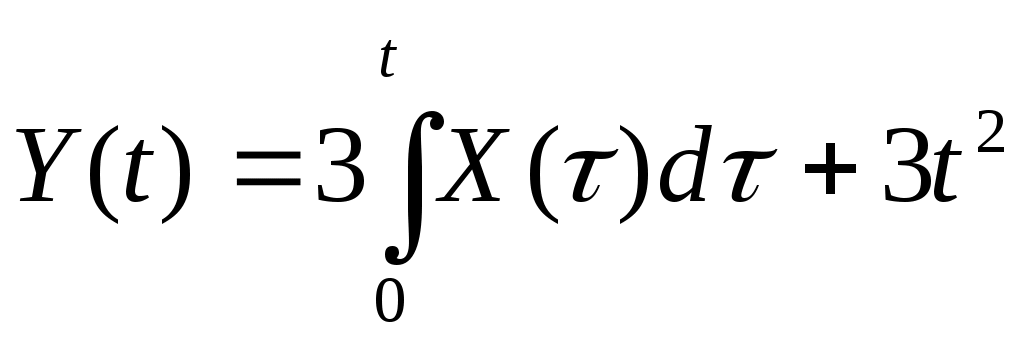 : : 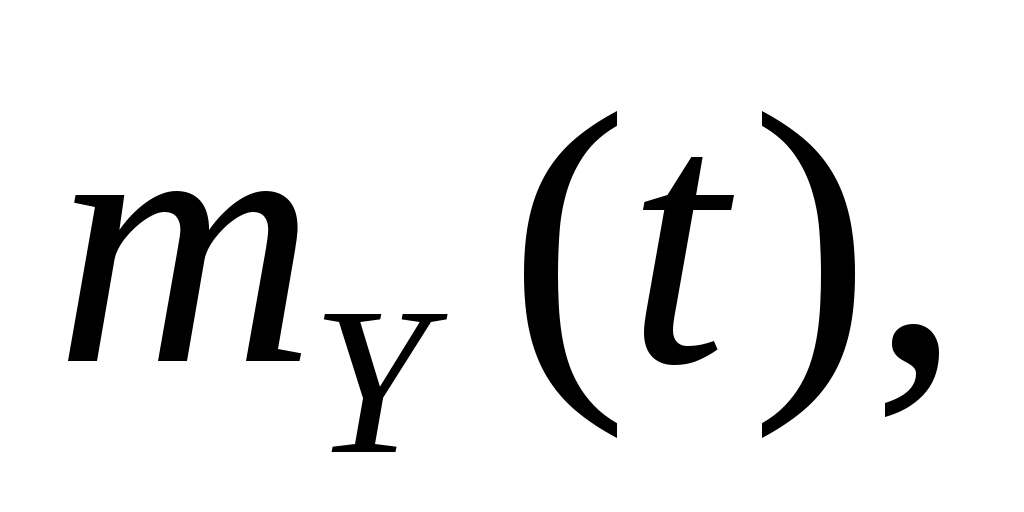 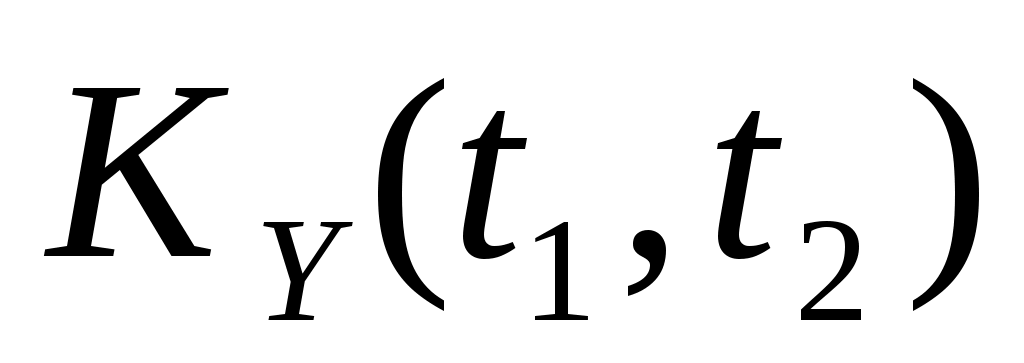 , , 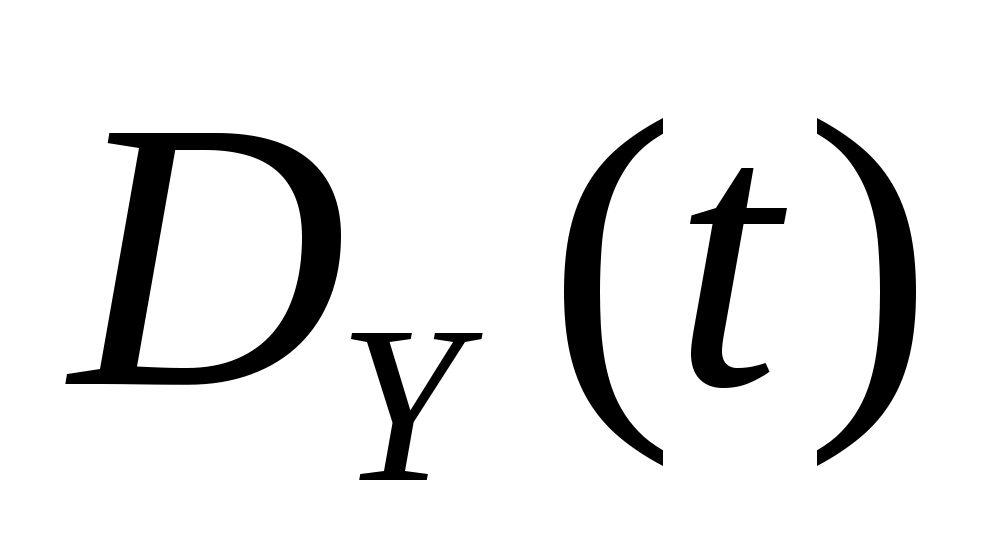 . .
3. Случайная функция 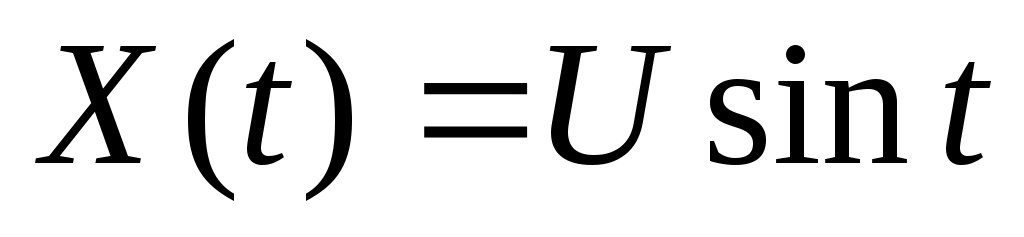 , где , где 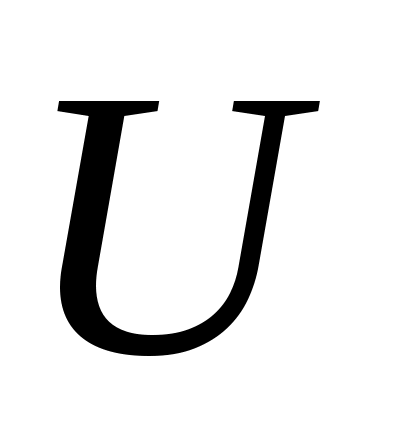 – случайная величина, распределенная по равномерному закону – случайная величина, распределенная по равномерному закону 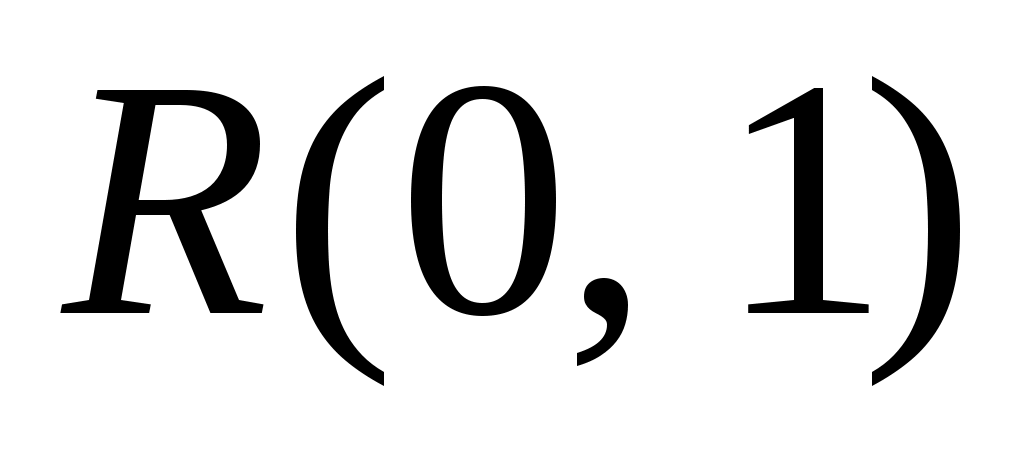 . Найти математическое ожидание и корреляционную функцию случайной функции . Найти математическое ожидание и корреляционную функцию случайной функции 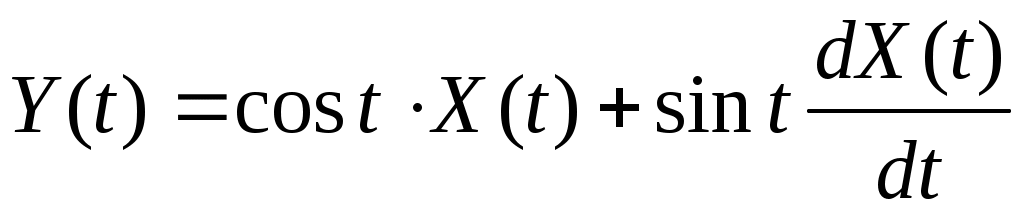 . .
4. Стационарная случайная функция 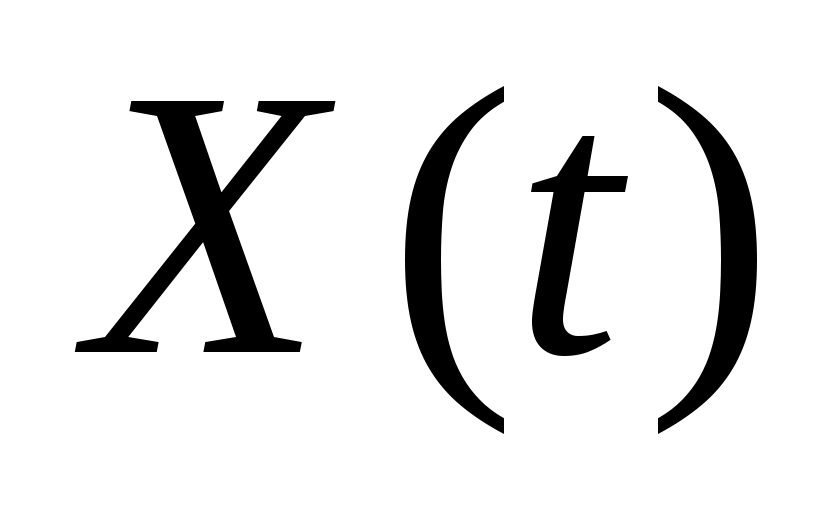 имеет корреляционную функцию имеет корреляционную функцию 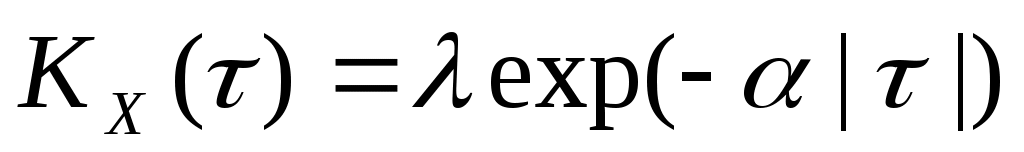 . Найти спектральную плотность . Найти спектральную плотность 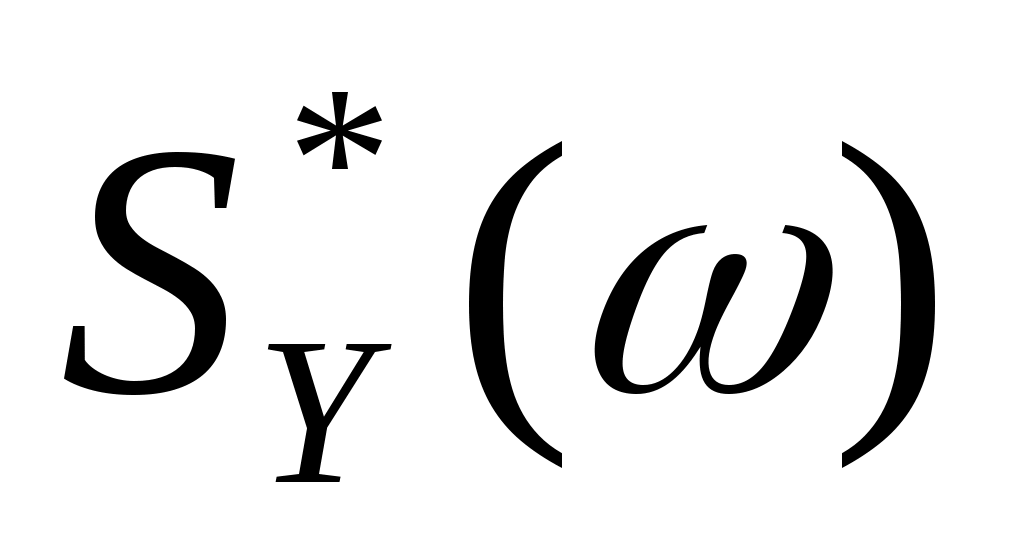 случайной функции случайной функции 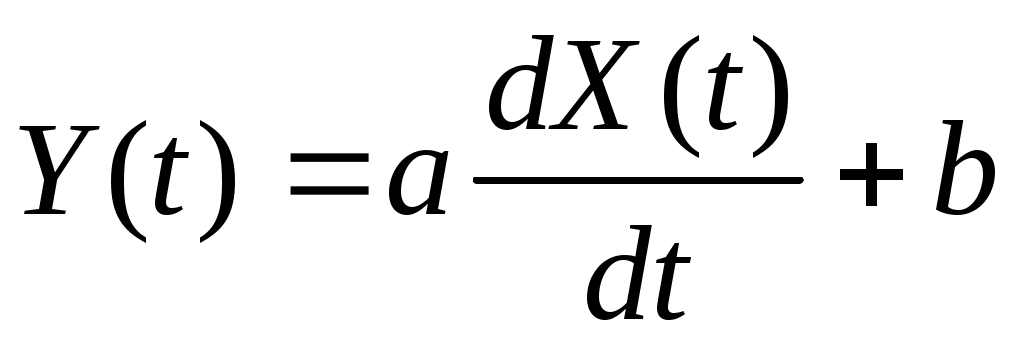 . .
5. На вход линейной динамической системы, описываемой уравнением 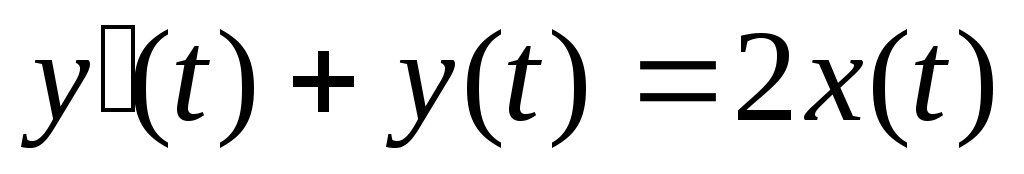 , поступает стационарный случайный процесс с характеристиками: , поступает стационарный случайный процесс с характеристиками: 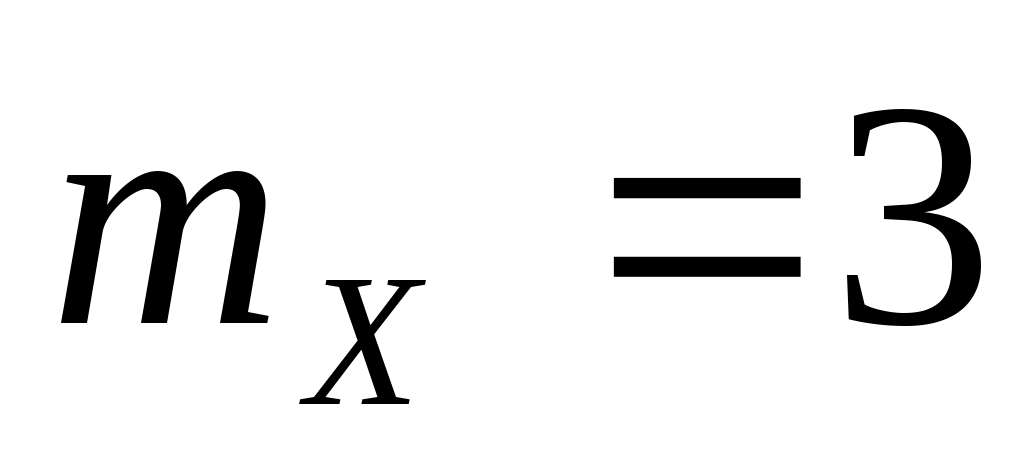 , , 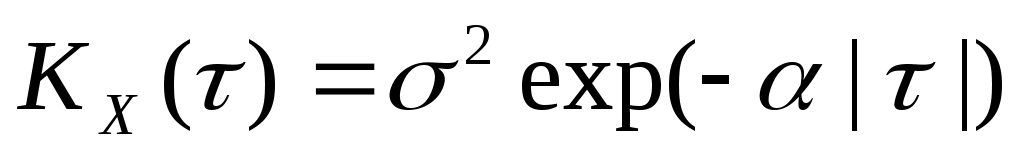 , , 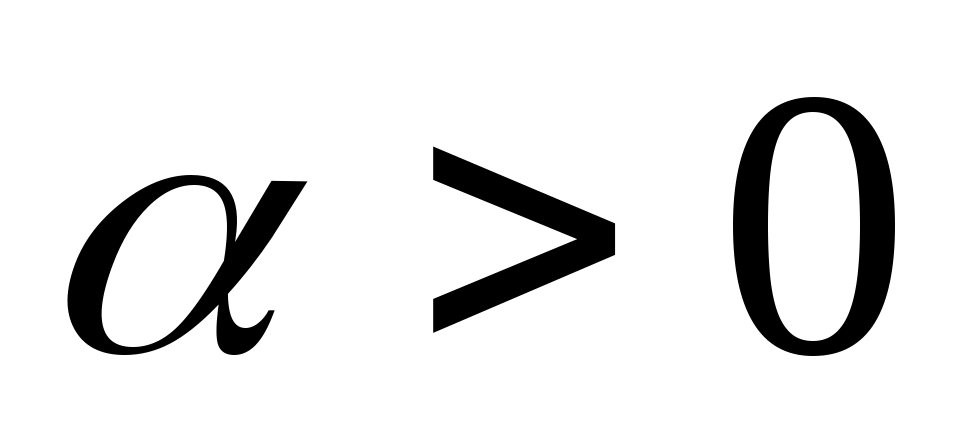 . Найти . Найти 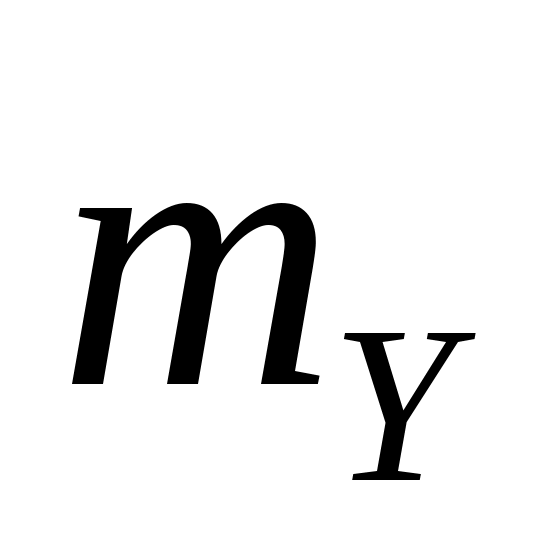 , , 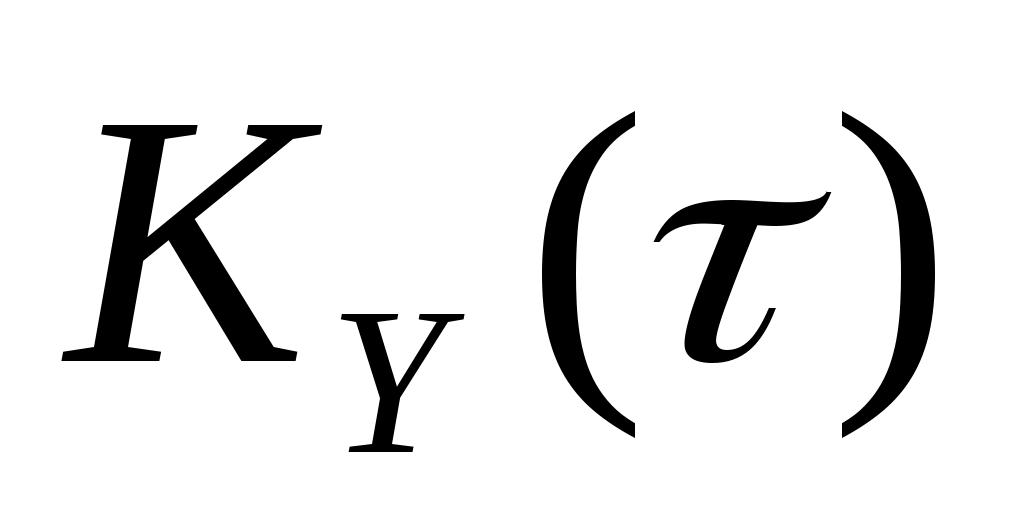 и и 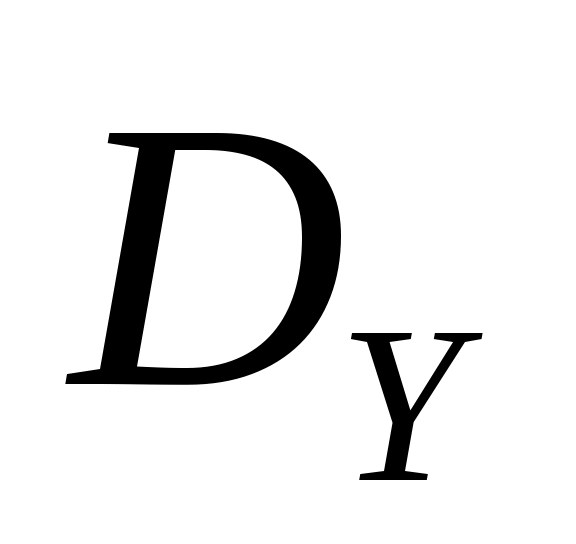 процесса процесса 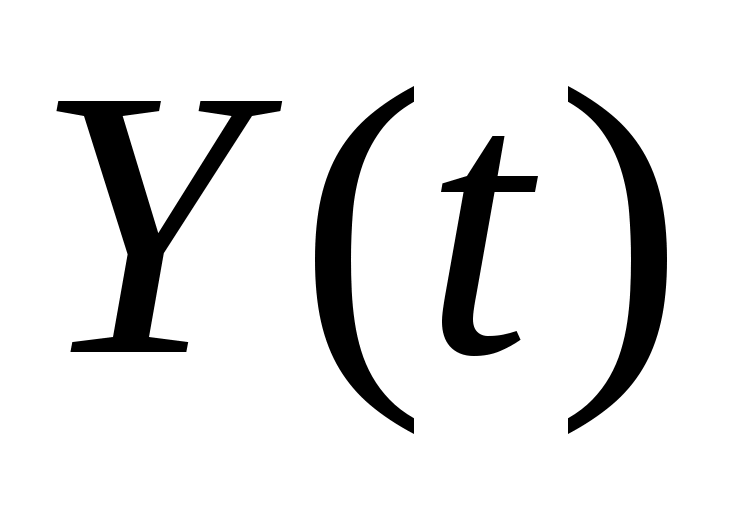 на выходе системы. на выходе системы.
Контрольная работа № 1
по дисциплине «Анализ случайных процессов»
Вариант № 11
1. Рассматривается случайная функция 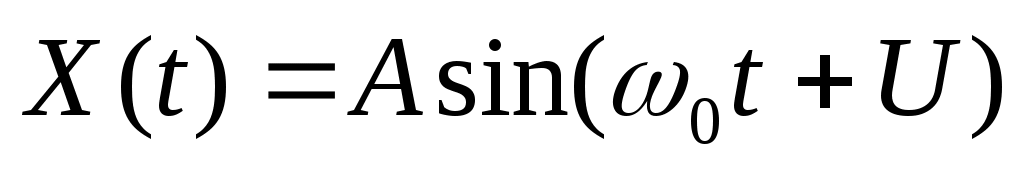 , где , где 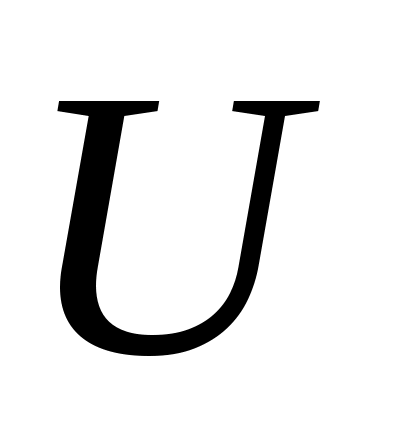 – случайная величина, распределенная по равномерному закону – случайная величина, распределенная по равномерному закону 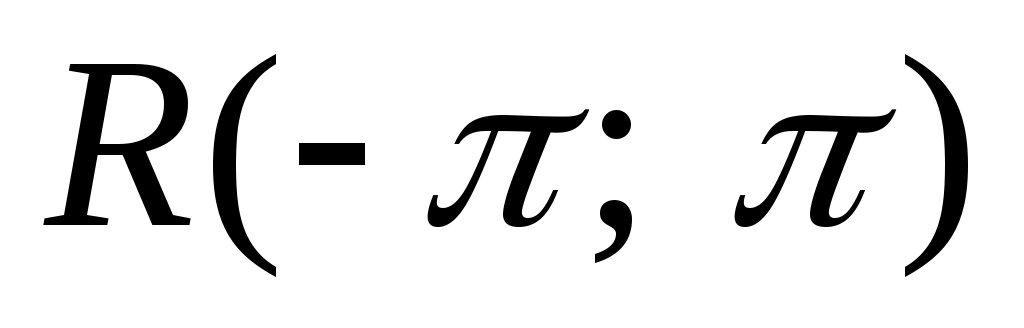 , ,  и и 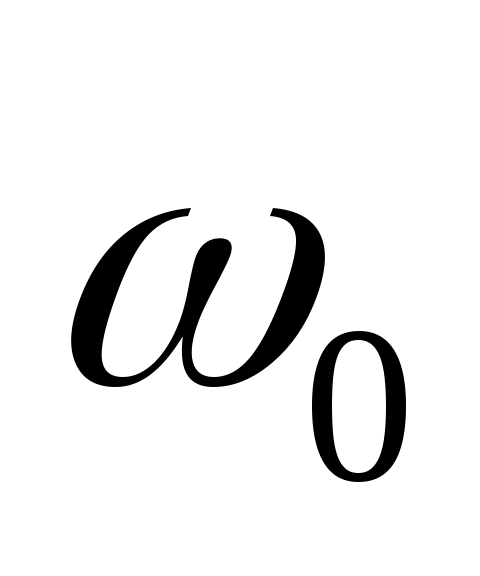 - константы. Найти математическое ожидание - константы. Найти математическое ожидание 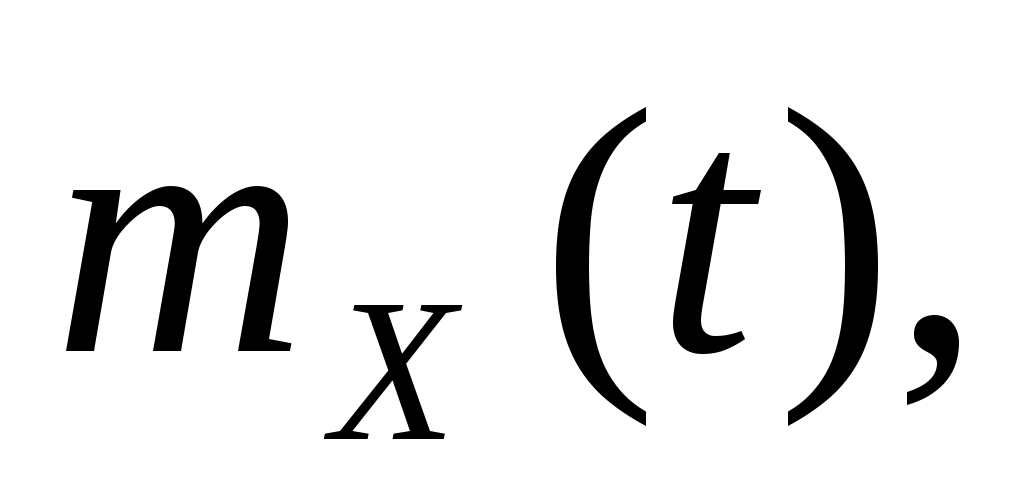 корреляционную функцию корреляционную функцию 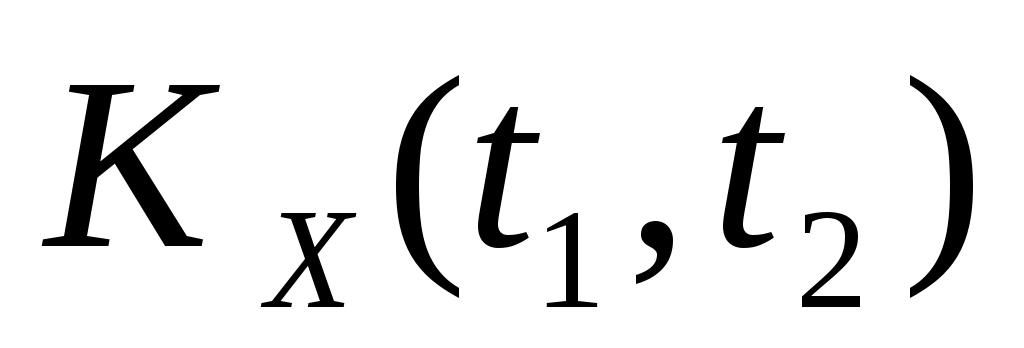 , дисперсию , дисперсию 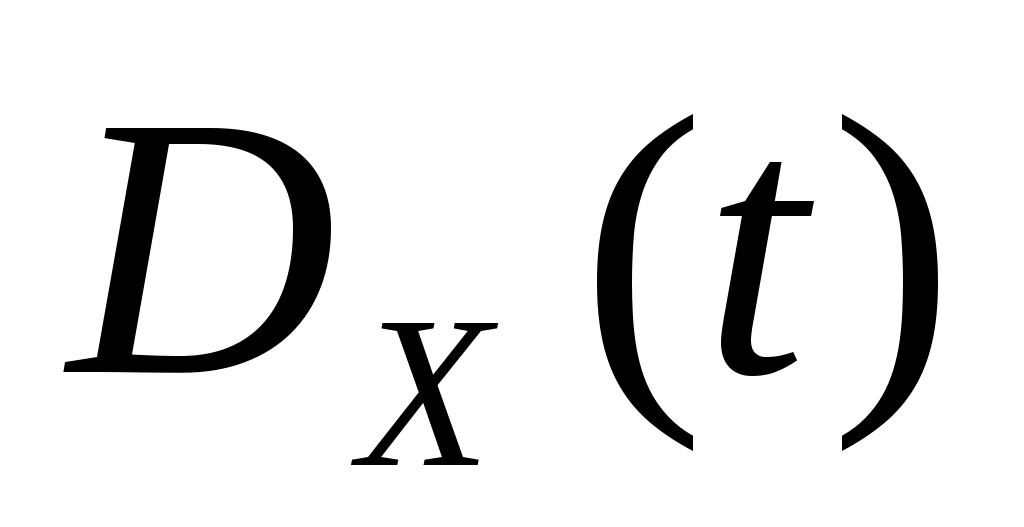 и и 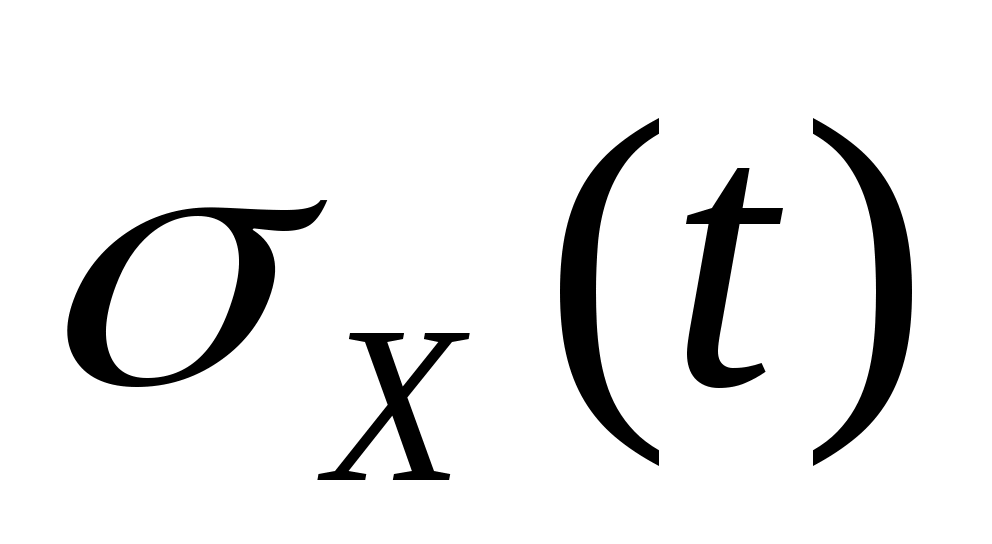 . Определить, является ли этот процесс стационарным. . Определить, является ли этот процесс стационарным.
2. Случайная функция 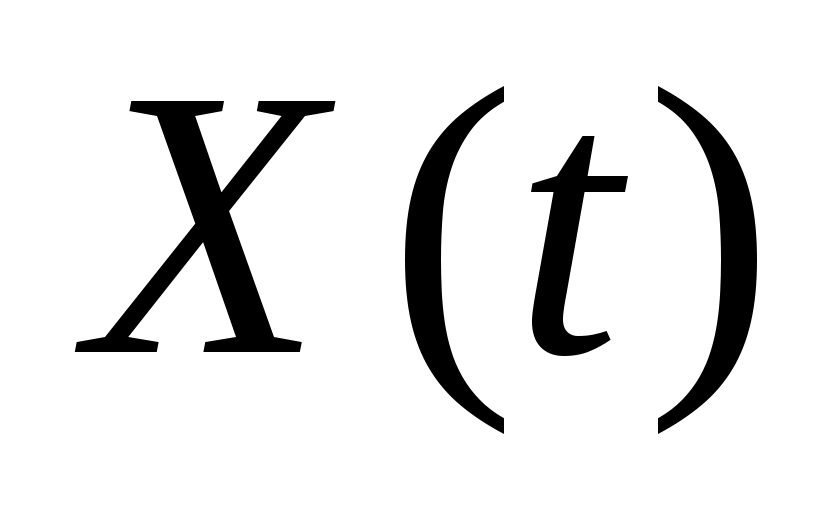 задана своим каноническим разложением задана своим каноническим разложением 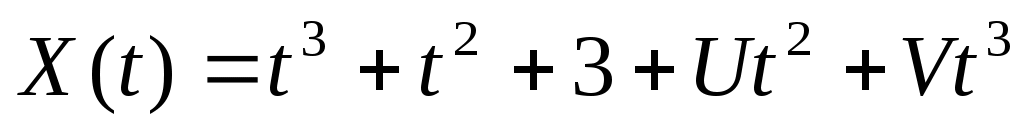 , где , где 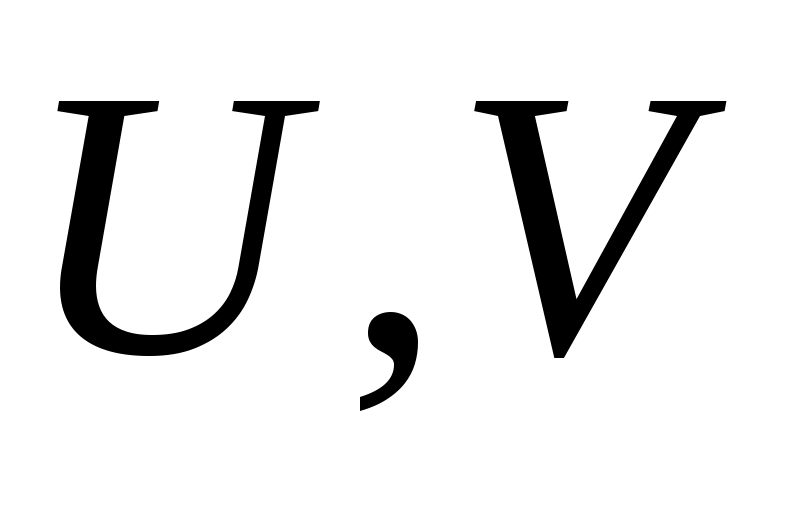 – некоррелированные случайные величины с м.о., равными нулю и дисперсиями – некоррелированные случайные величины с м.о., равными нулю и дисперсиями 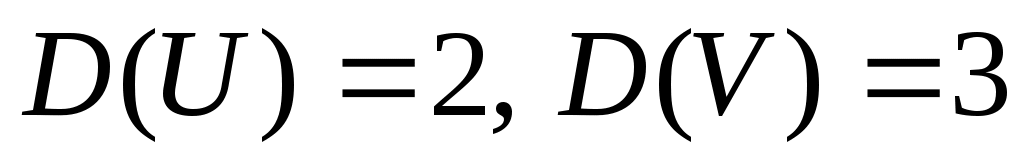 . Найти характеристики . Найти характеристики 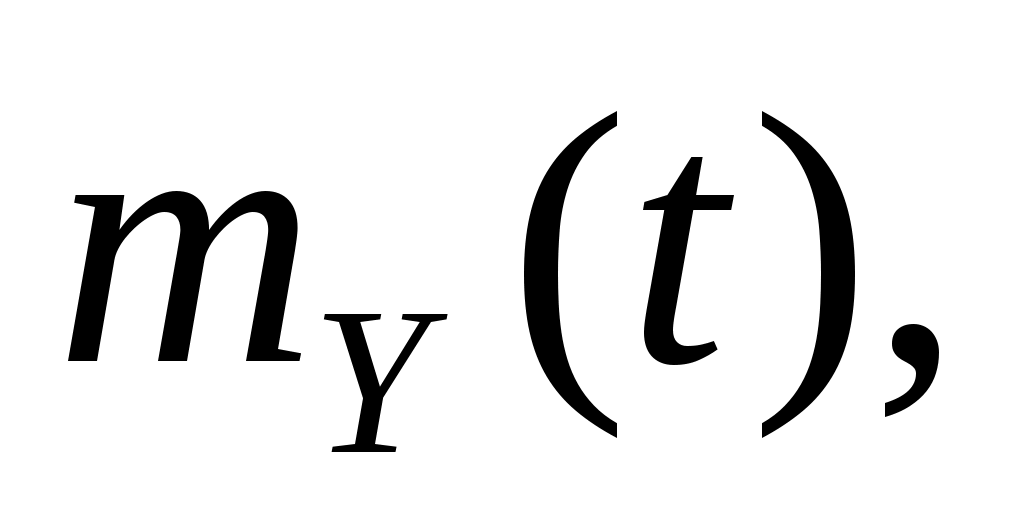 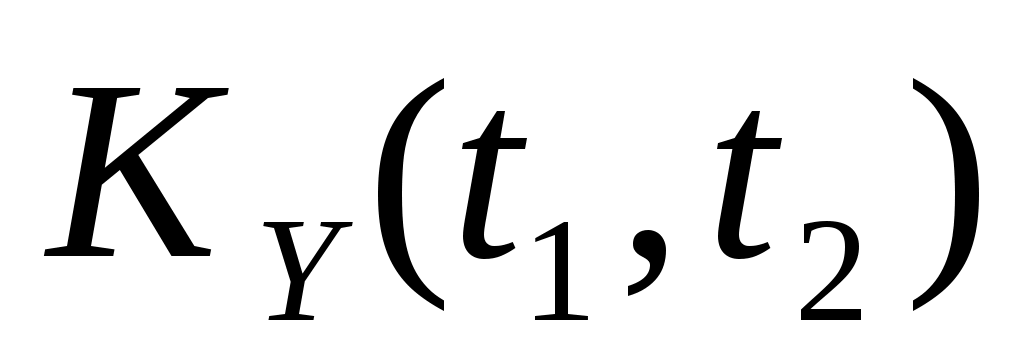 случайной функции случайной функции 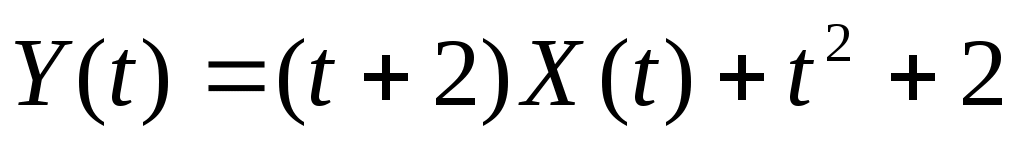 . .
3. Дана случайная функция 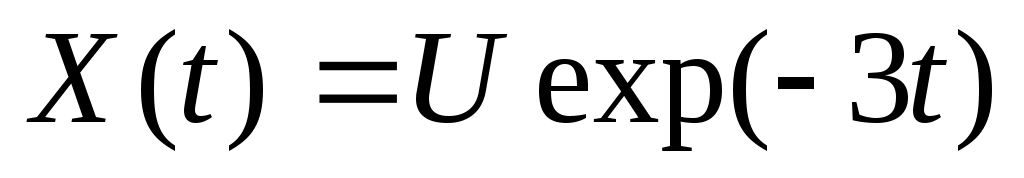 , где , где 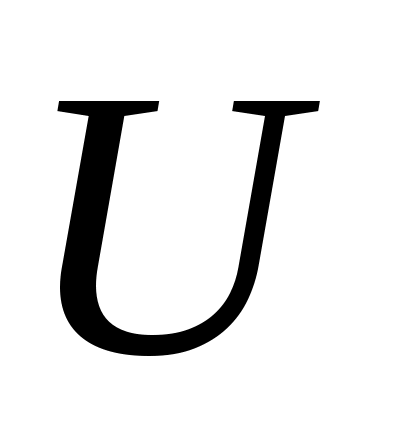 – случайная величина, распределенная по показательному закону – случайная величина, распределенная по показательному закону 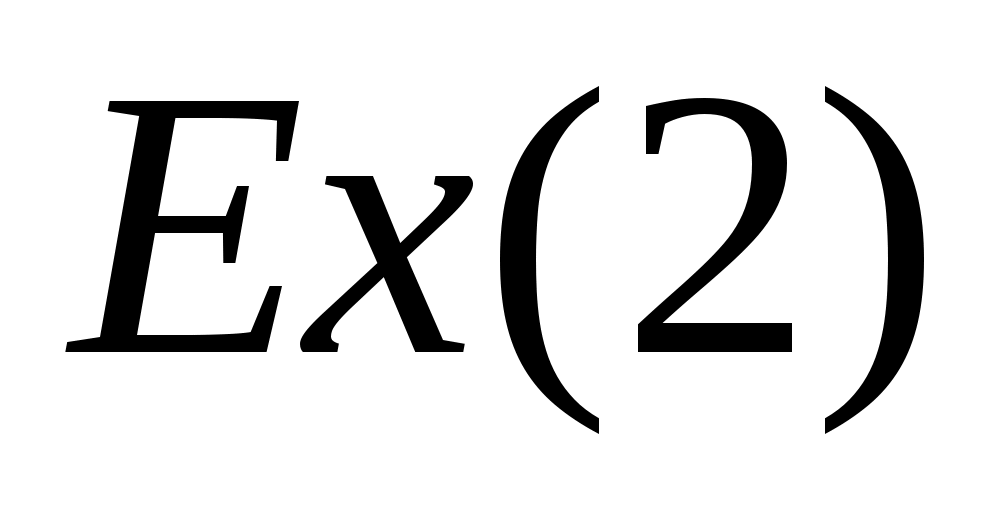 . Найти характеристики случайной функции . Найти характеристики случайной функции 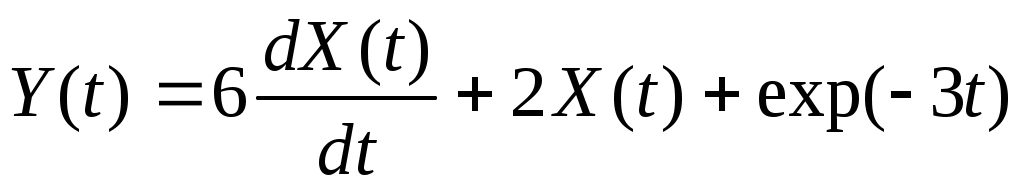 : :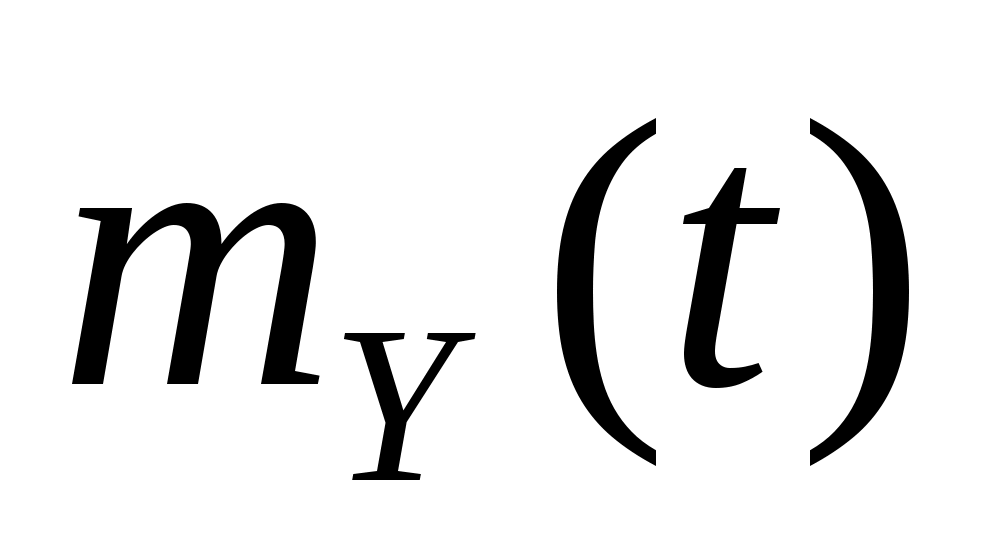 , , 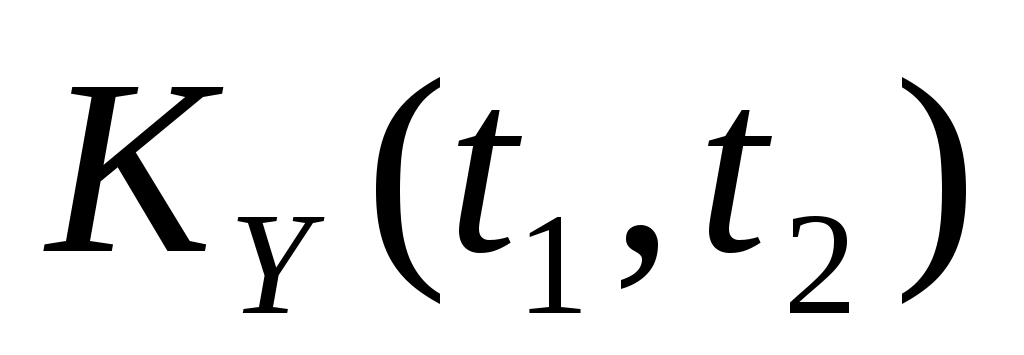 , , 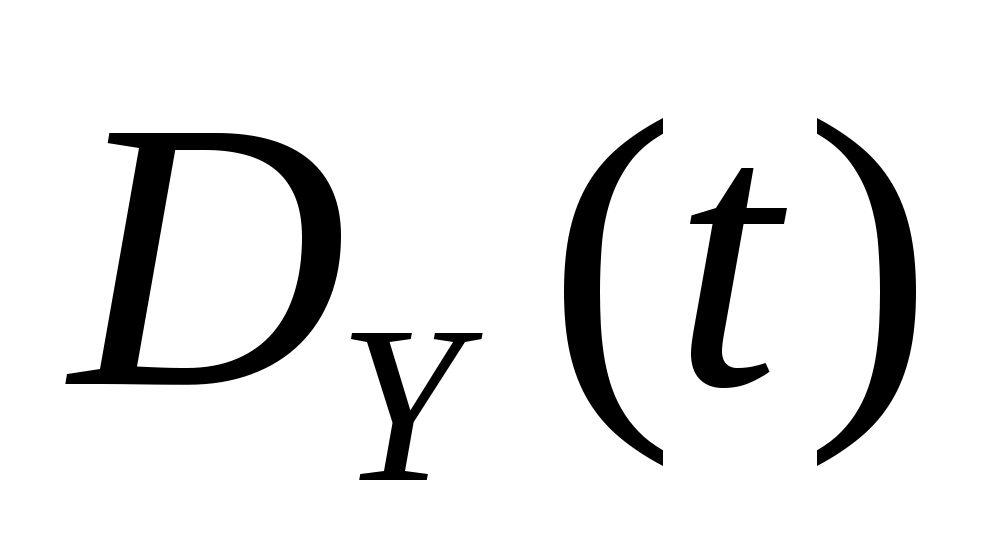 . .
4. Стационарная случайная функция 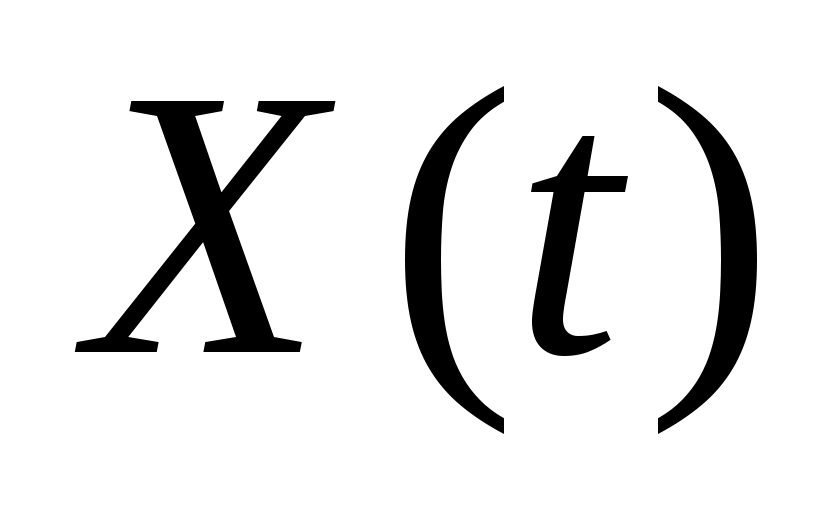 имеет корреляционную функцию имеет корреляционную функцию 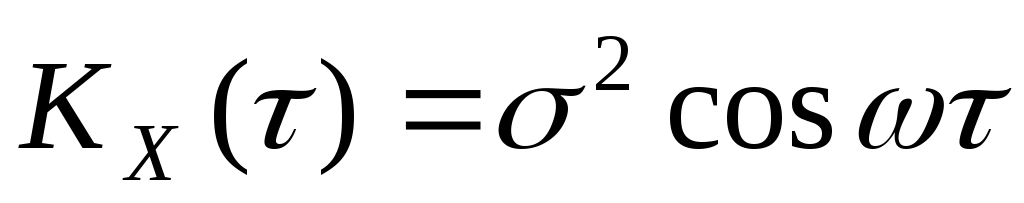 . Найти корреляционную функцию случайной функции . Найти корреляционную функцию случайной функции 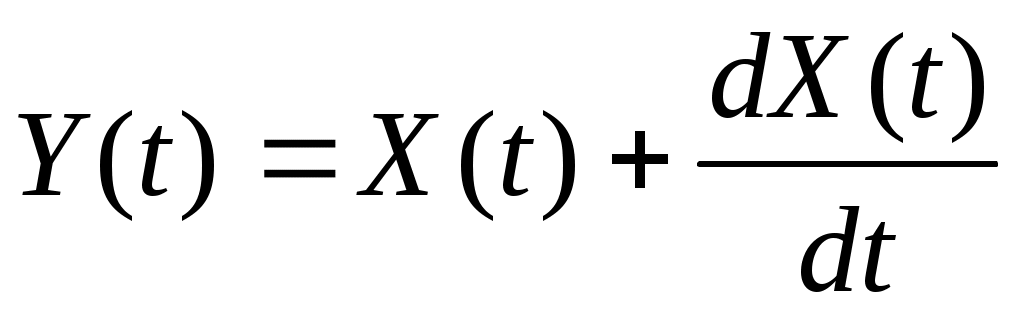 . .
5. Стационарная случайная функция 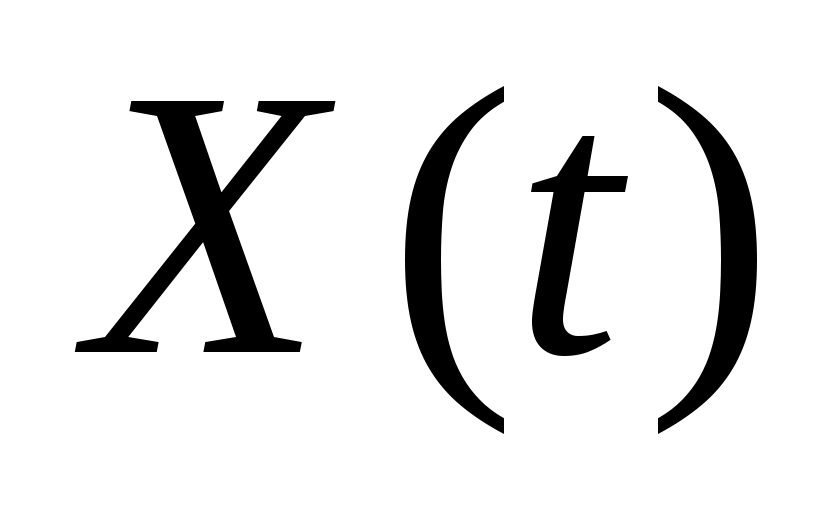 имеет спектральную плотность имеет спектральную плотность 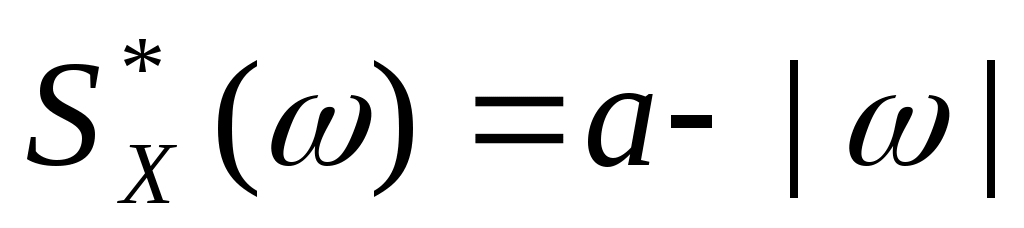 , , 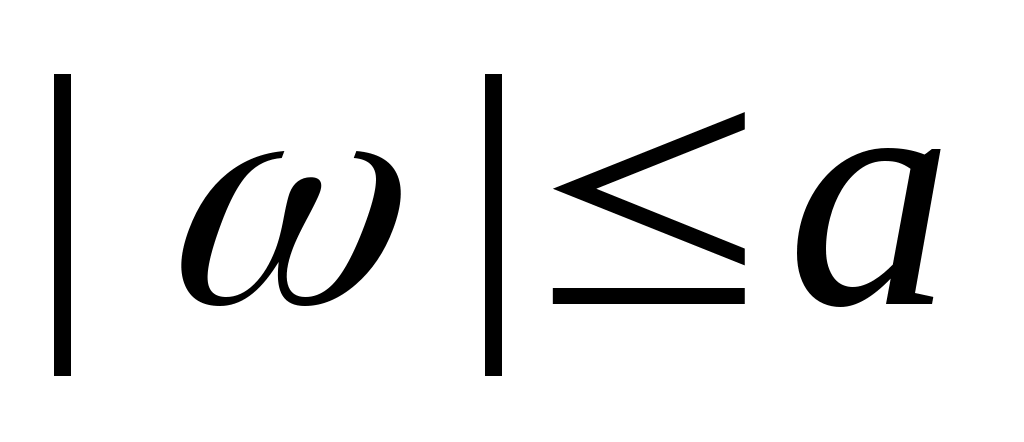 , , 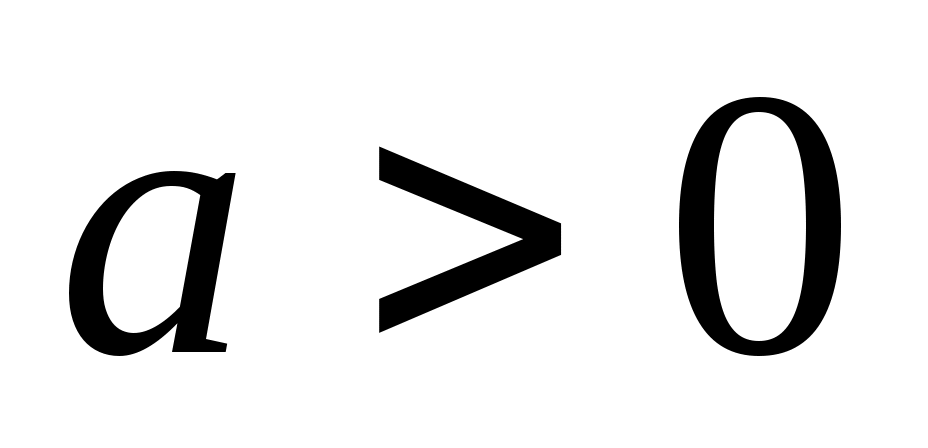 . Найти спектральную плотность и дисперсию случайной функции . Найти спектральную плотность и дисперсию случайной функции 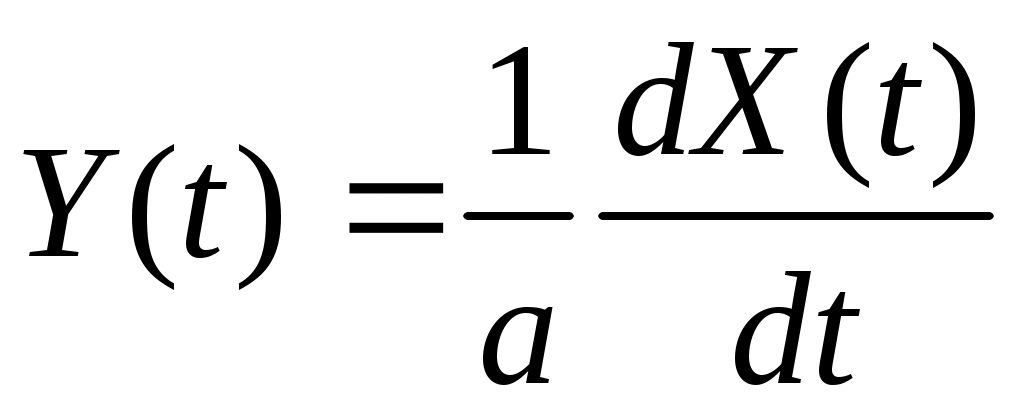 . .
К онтрольная работа № 1 онтрольная работа № 1
по дисциплине «Анализ случайных процессов»
Вариант № 12
1. Рассматривается случайная функция 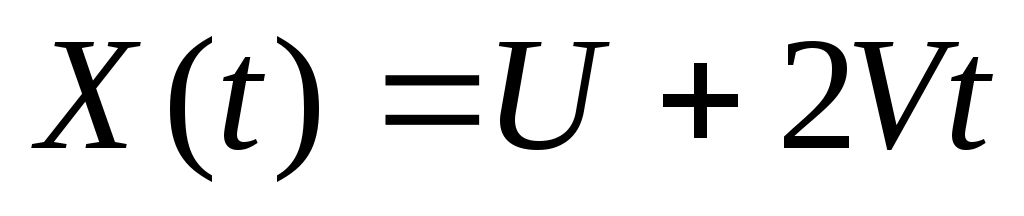 , где , где 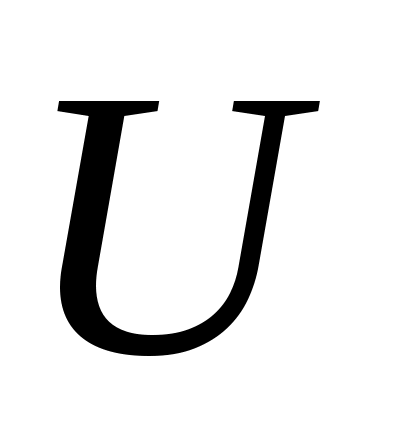 , , 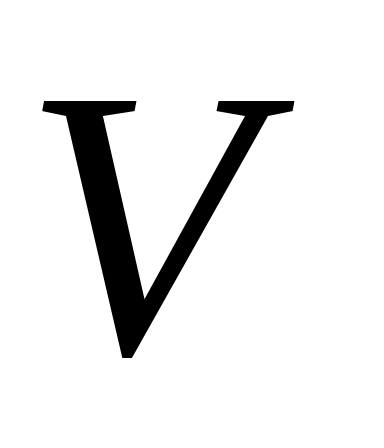 – некоррелированные случайные величины, распределенные по нормальным законам – некоррелированные случайные величины, распределенные по нормальным законам 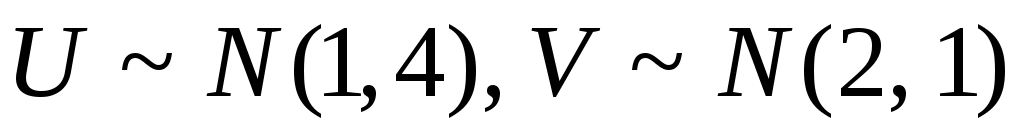 . Найти плотность распределения сечения этой функции и характеристики . Найти плотность распределения сечения этой функции и характеристики 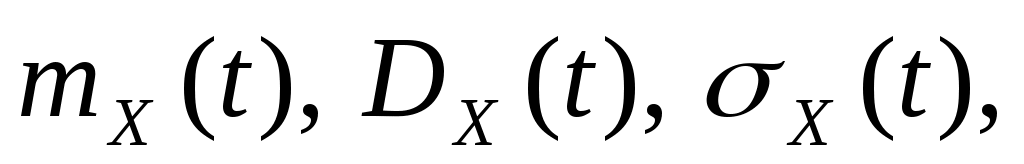 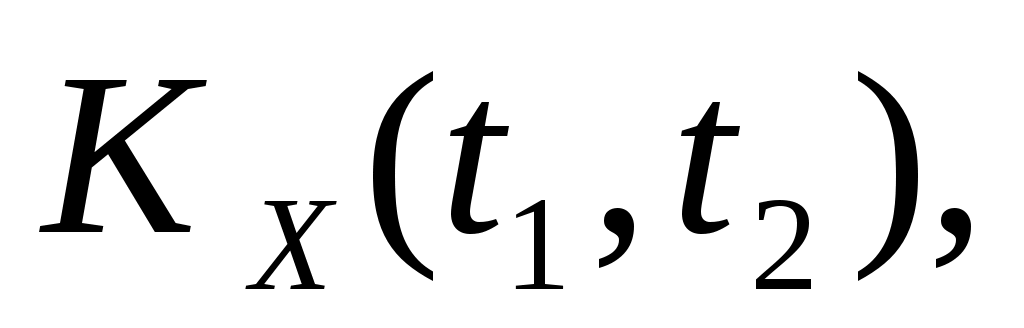 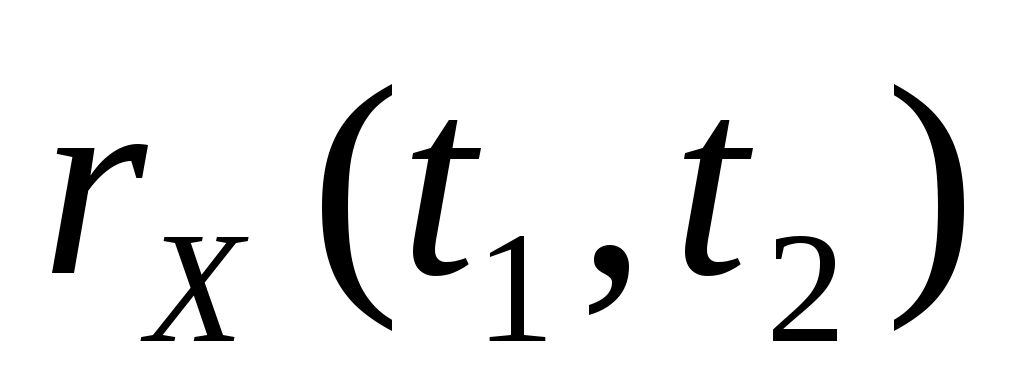 . .
2. Случайный процесс 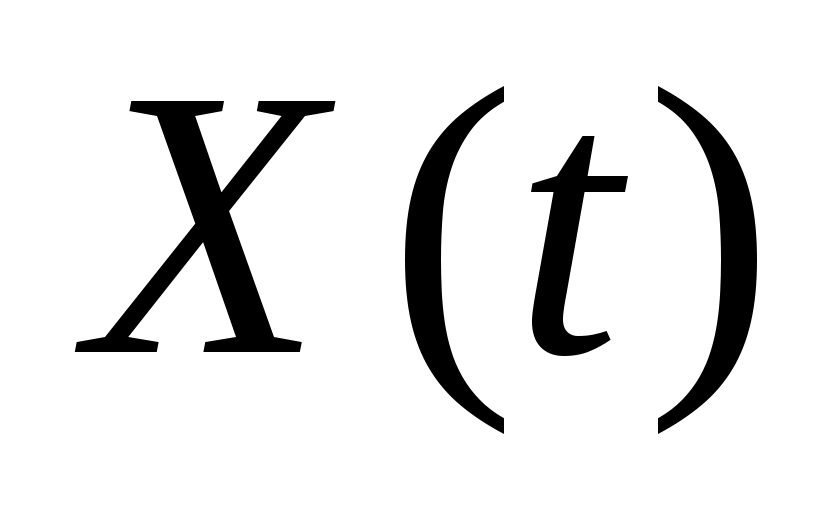 имеет характеристики имеет характеристики 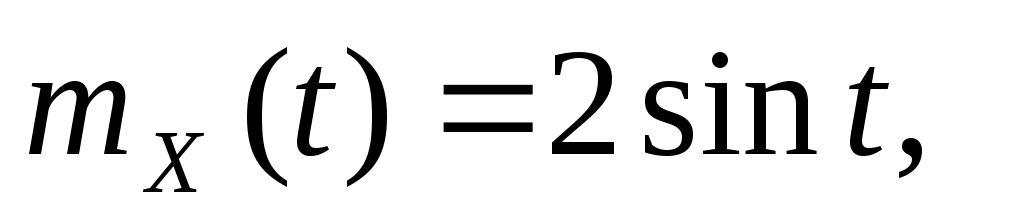 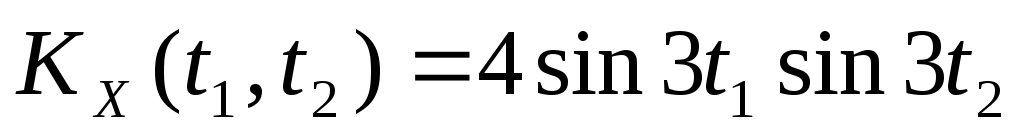 . Найти характеристики случайного процесса . Найти характеристики случайного процесса 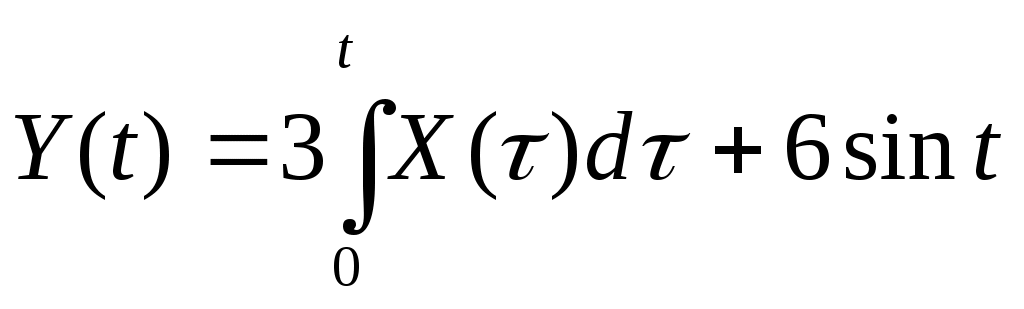 : : 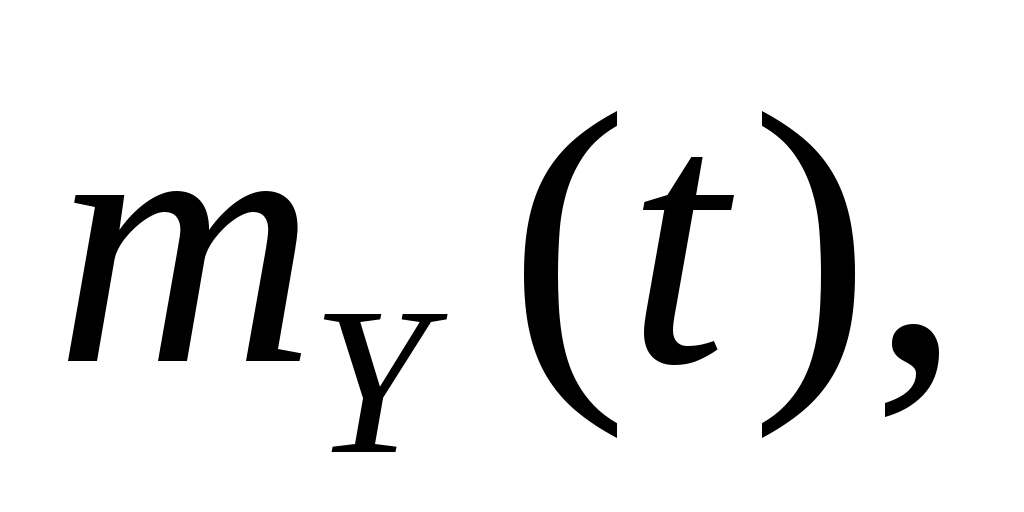 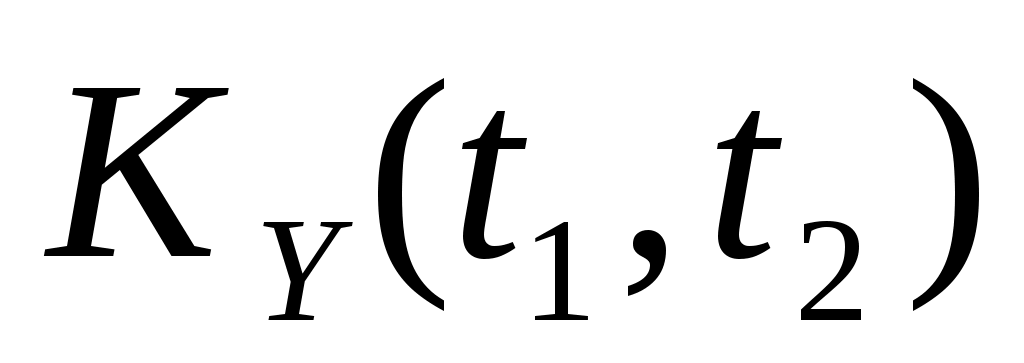 , , 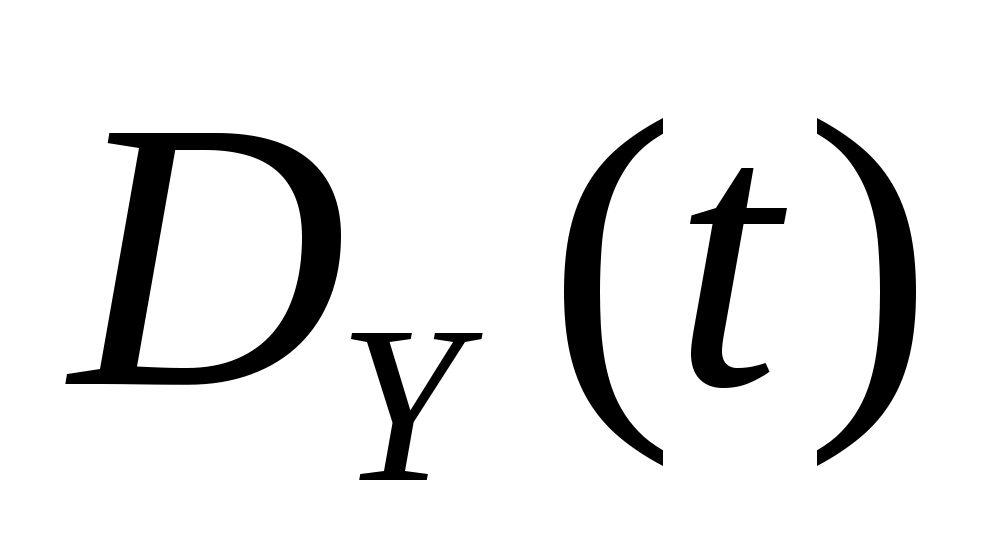 . .
3. Случайная функция 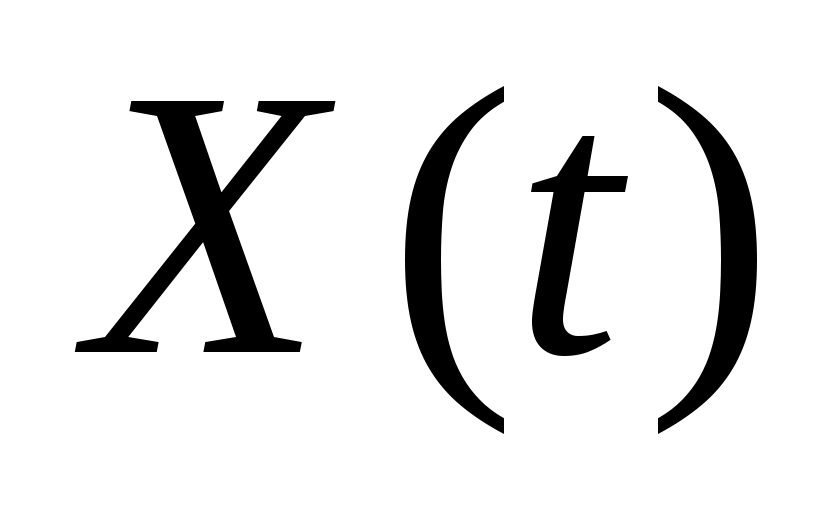 задана своим каноническим разложением задана своим каноническим разложением 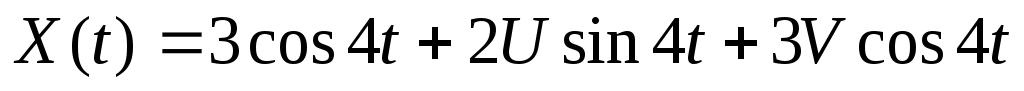 , где , где 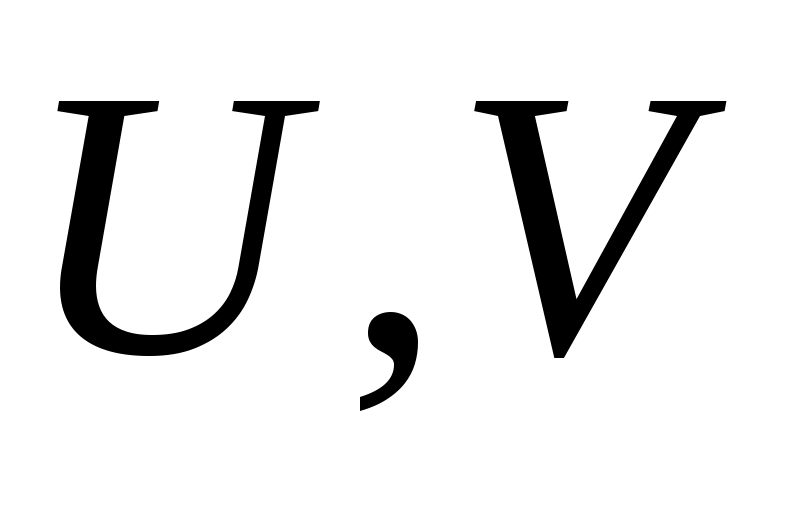 – некоррелированные случайные величины с м.о., равными нулю, и дисперсиями – некоррелированные случайные величины с м.о., равными нулю, и дисперсиями 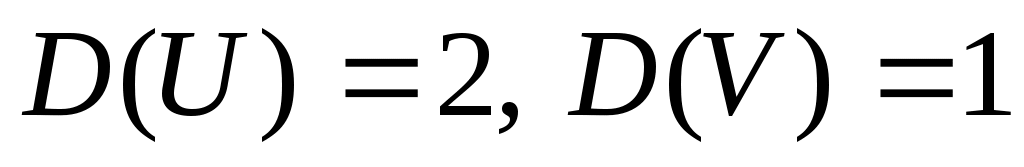 . Найти характеристики c.ф. . Найти характеристики c.ф. 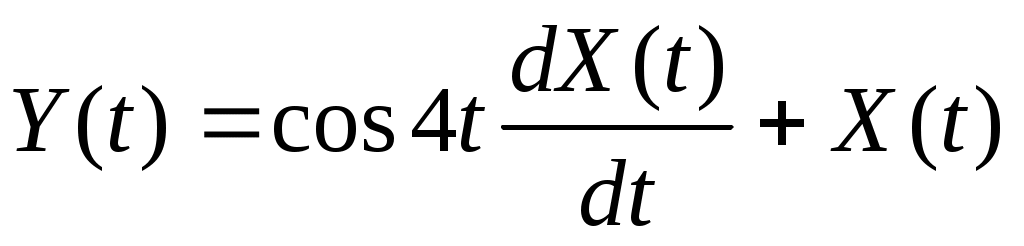 : : 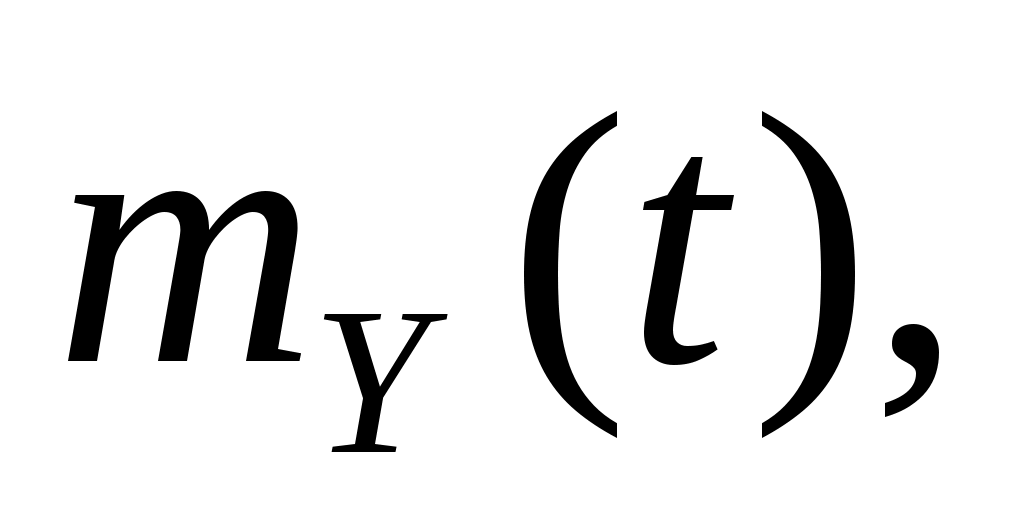 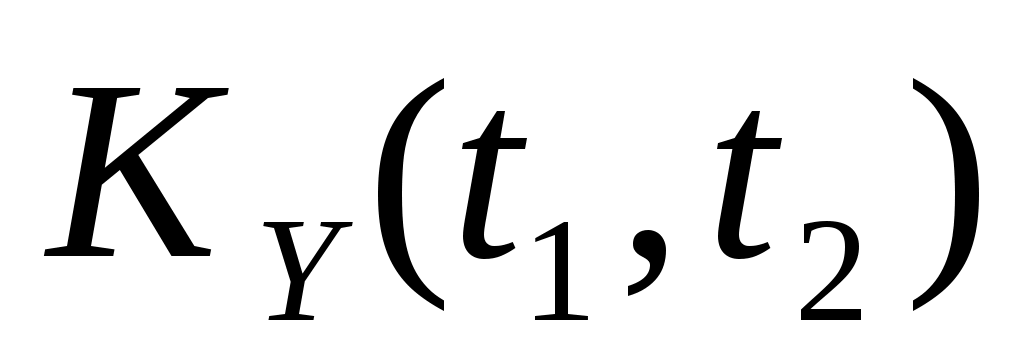 . .
4. Стационарная случайная функция 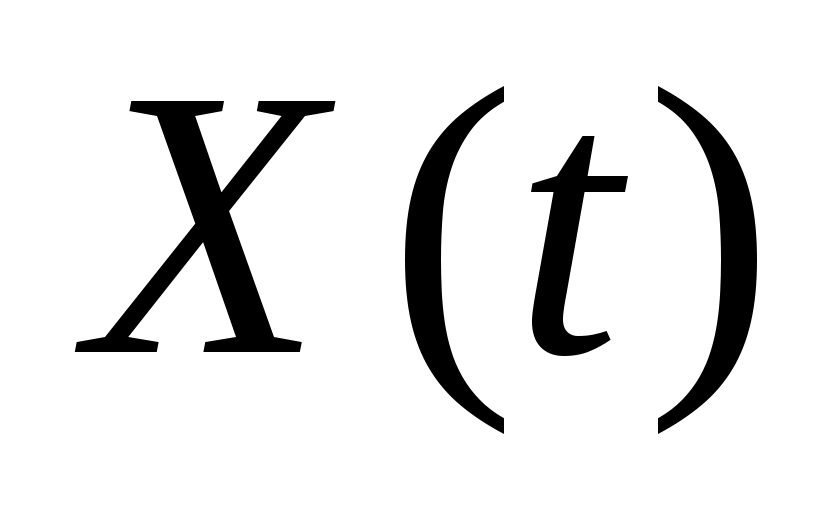 имеет корреляционную функцию имеет корреляционную функцию 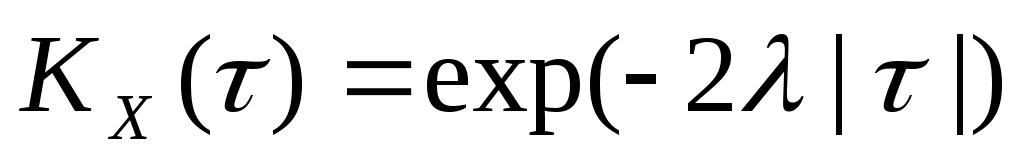 . Найти взаимную корреляционную функцию случайных функций . Найти взаимную корреляционную функцию случайных функций 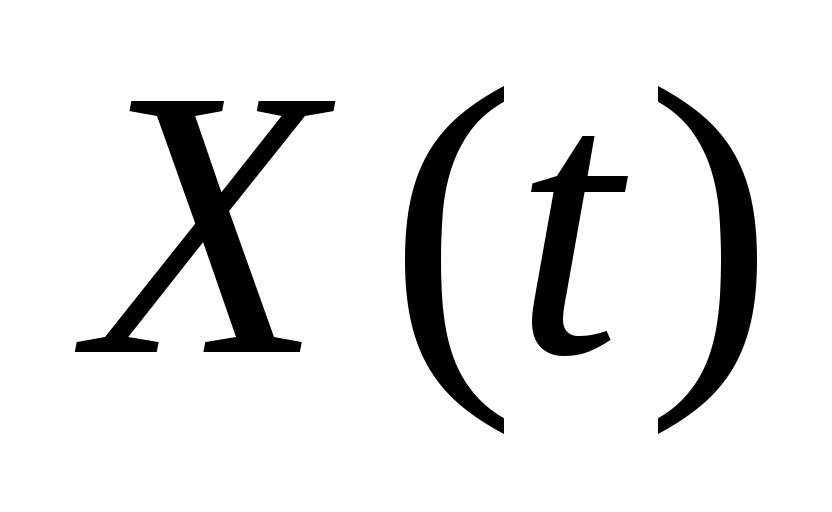 и и 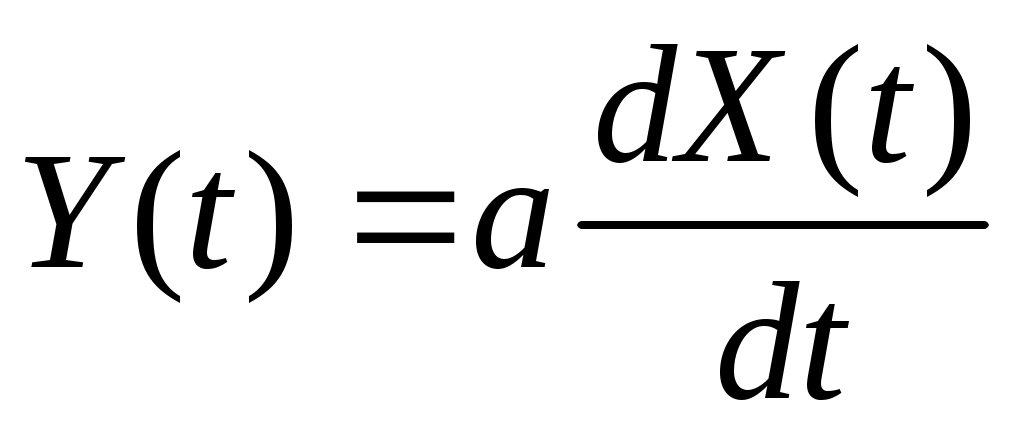 . .
5. Спектральная плотность случайной функции 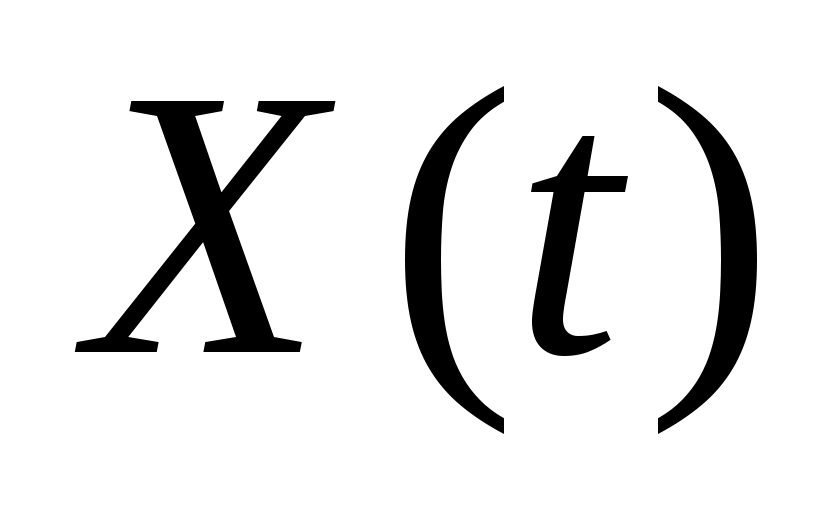 имеет вид: имеет вид: 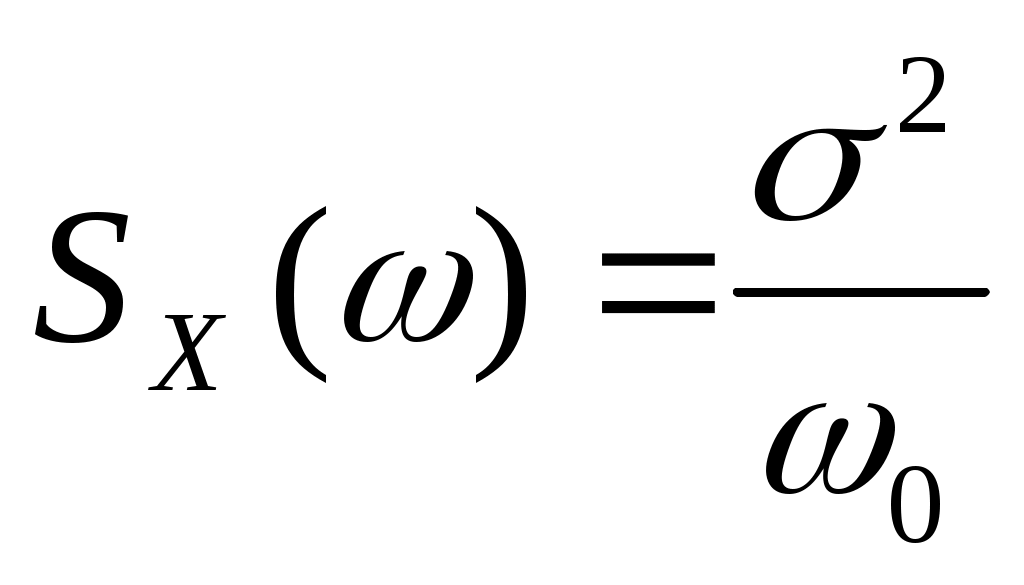 , , 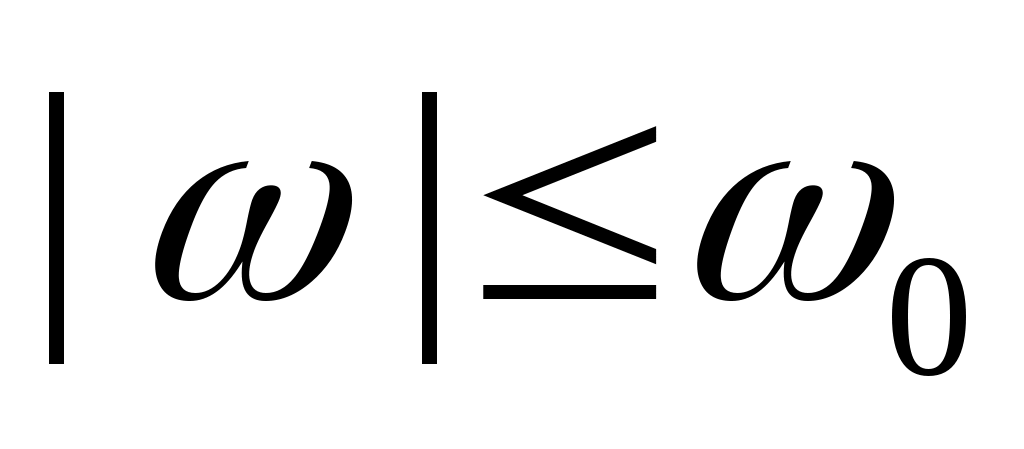 , , 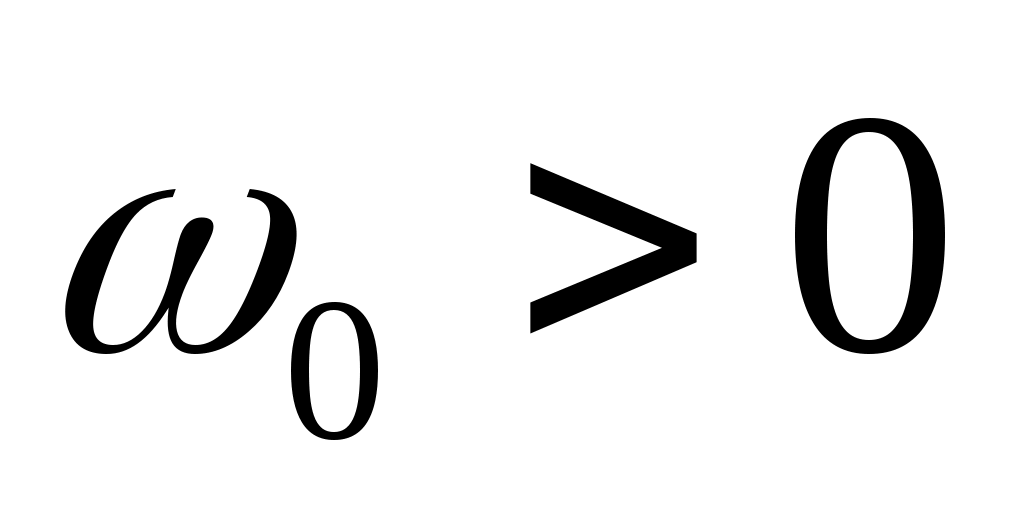 . Найти дисперсию случайной функции . Найти дисперсию случайной функции 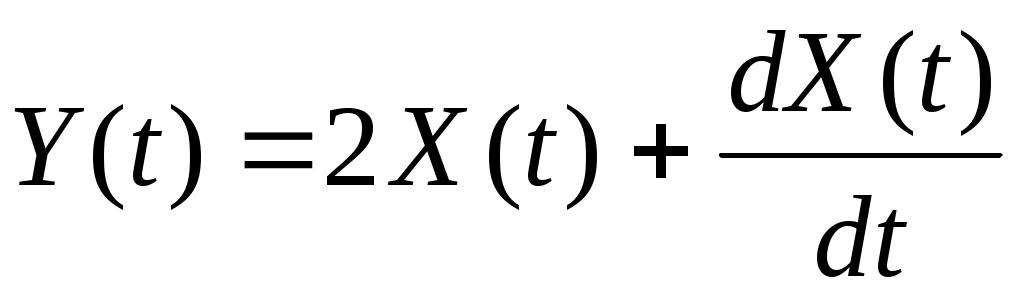 . .
Контрольная работа № 1
по дисциплине «Анализ случайных процессов»
Вариант № 13
1. Рассматривается случайная функция 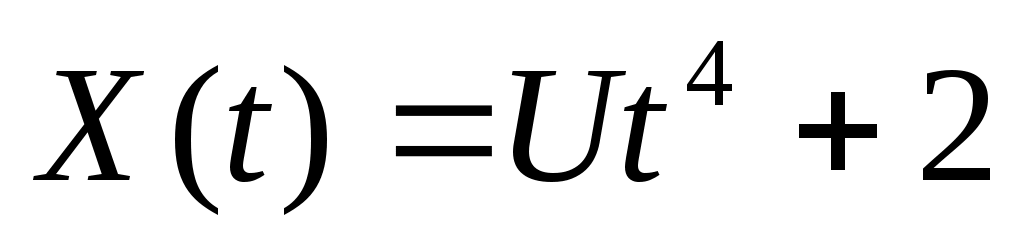 , где , где 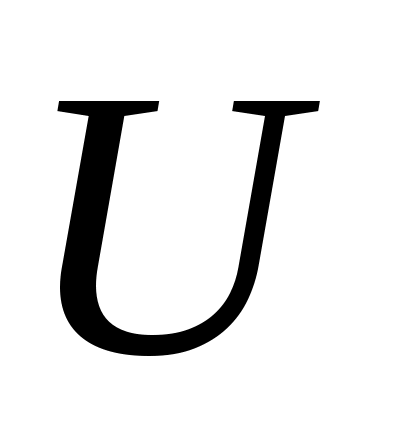 – случайная величина, распределенная по равномерному закону – случайная величина, распределенная по равномерному закону 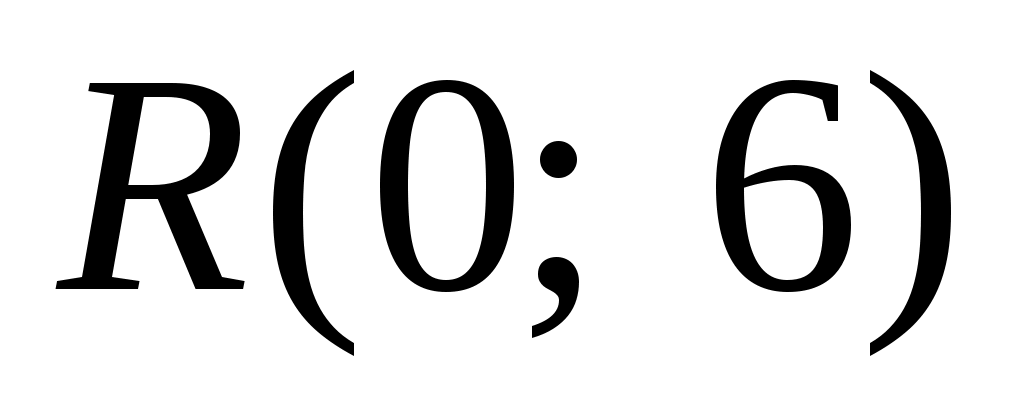 . Найти плотность распределения сечения этой функции и характеристики . Найти плотность распределения сечения этой функции и характеристики 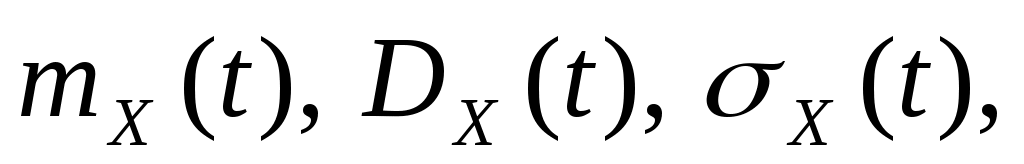 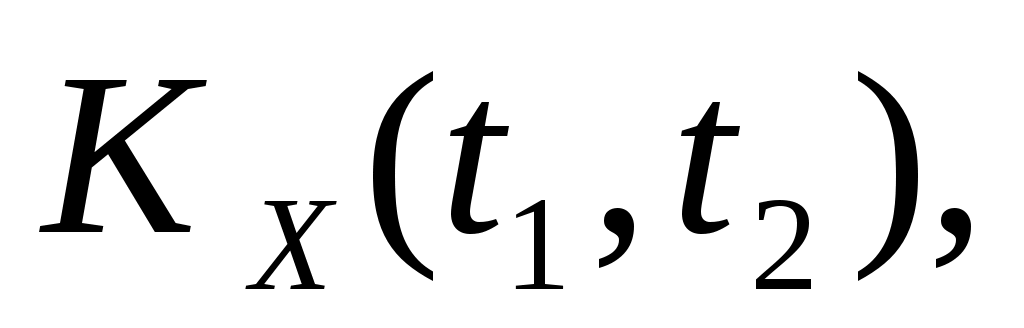 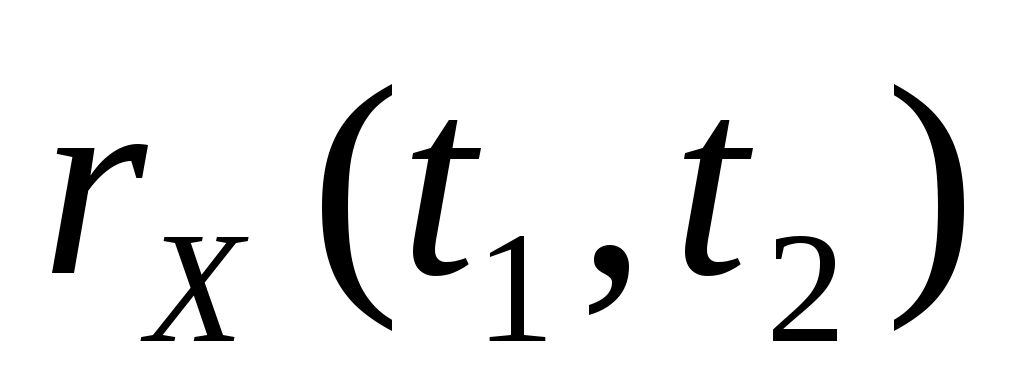 . .
2. Случайная функция 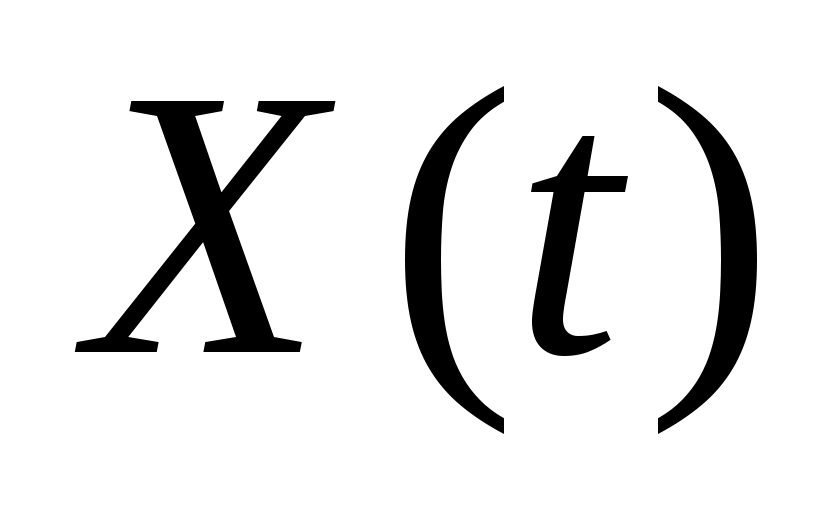 задана своим каноническим разложением задана своим каноническим разложением 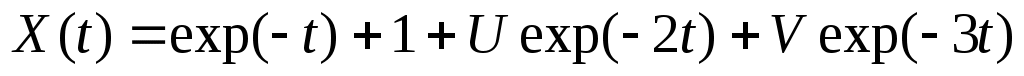 , где , где 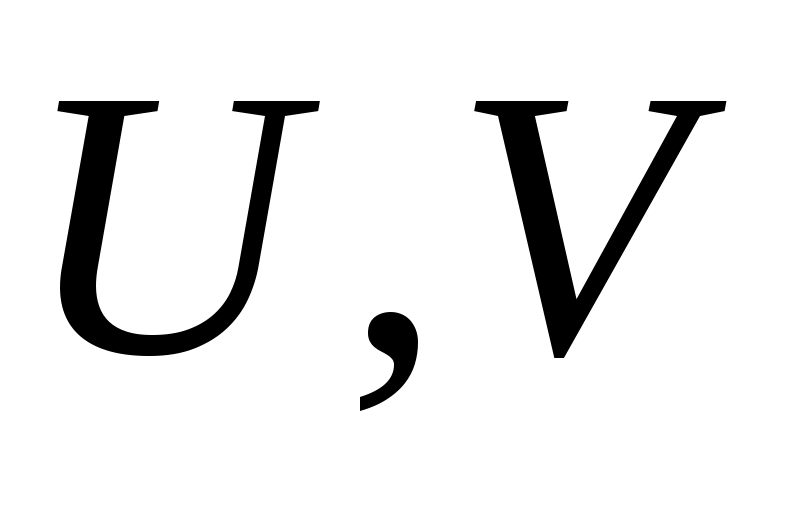 – некоррелированные случайные величины с м.о., равными нулю и дисперсиями – некоррелированные случайные величины с м.о., равными нулю и дисперсиями 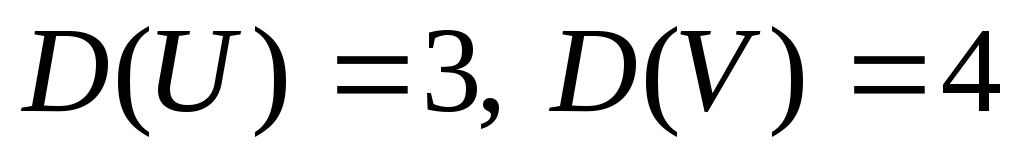 . Найти характеристики случайной функции . Найти характеристики случайной функции 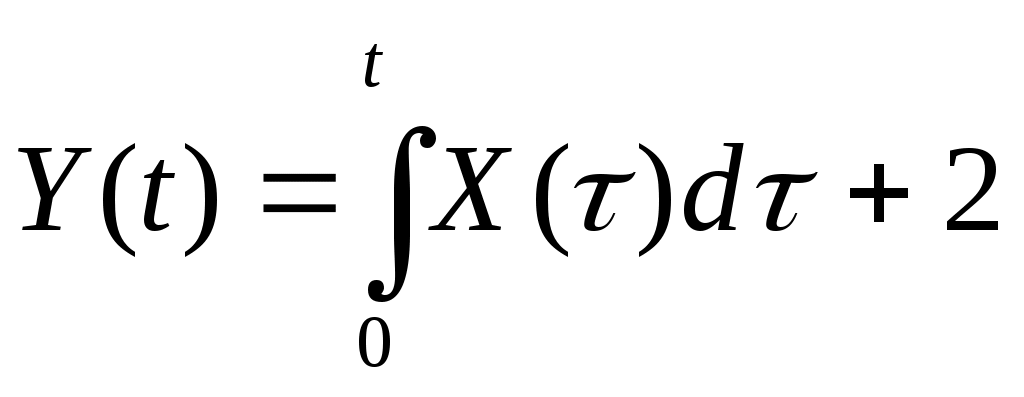 : : 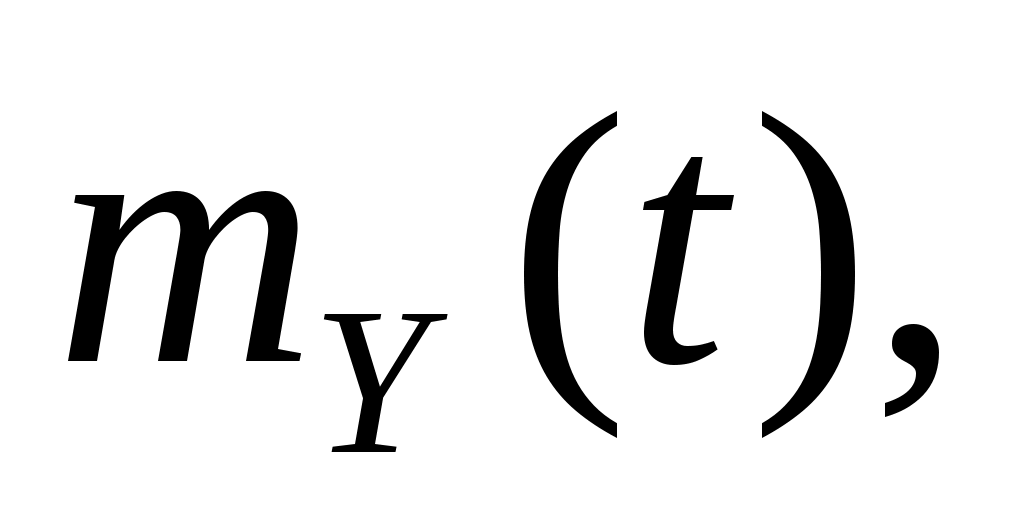 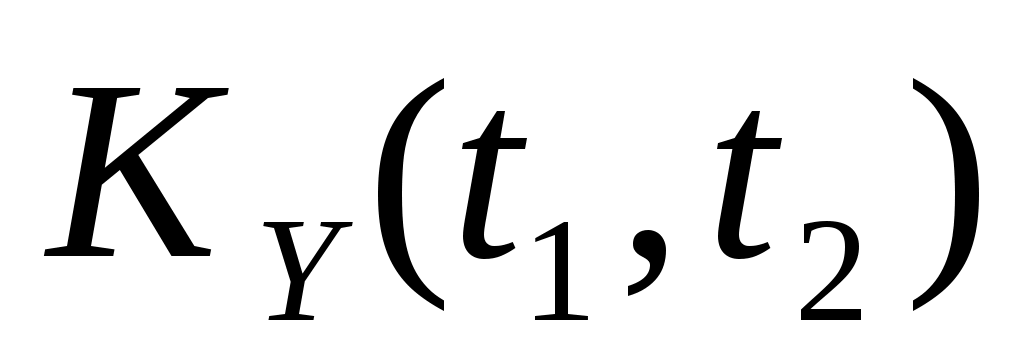 . .
3. Случайная функция 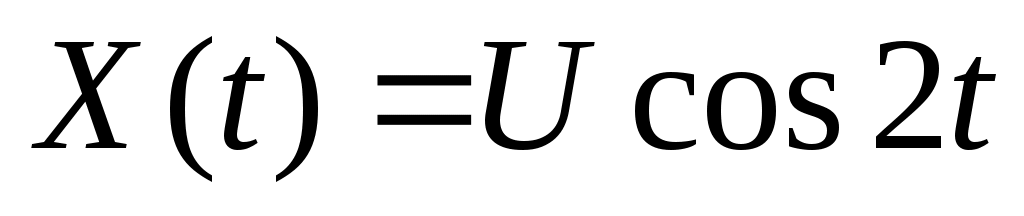 , где , где 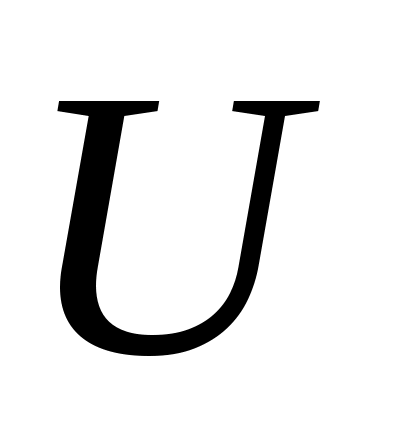 – случайная величина, распределенная по экспоненциальному закону – случайная величина, распределенная по экспоненциальному закону 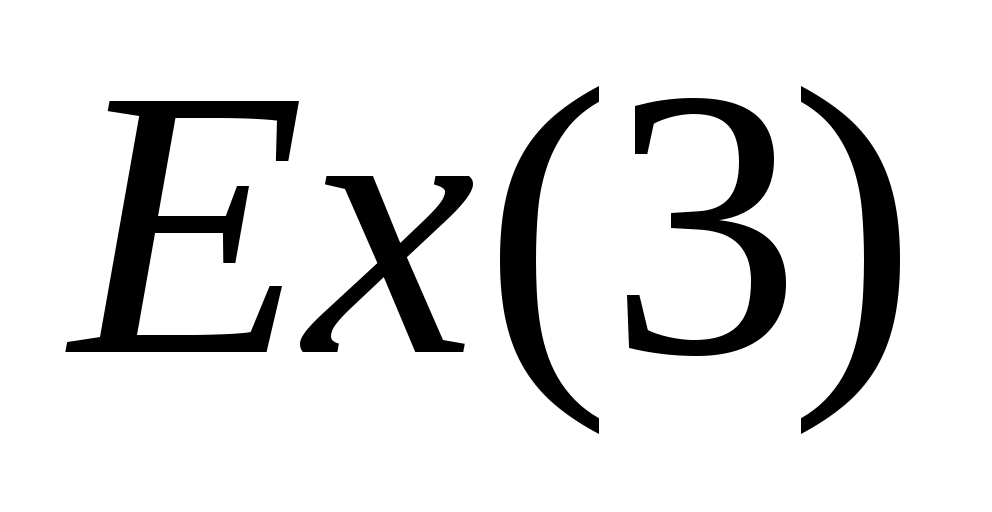 . Найти математическое ожидание и корреляционную функцию случайной функции . Найти математическое ожидание и корреляционную функцию случайной функции 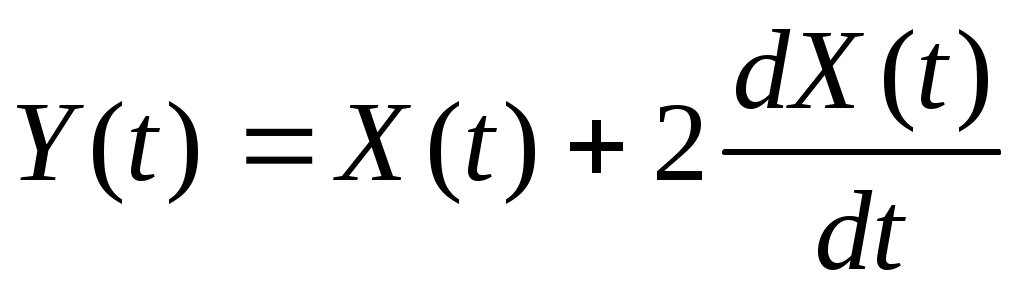 . .
4. Стационарная случайная функция 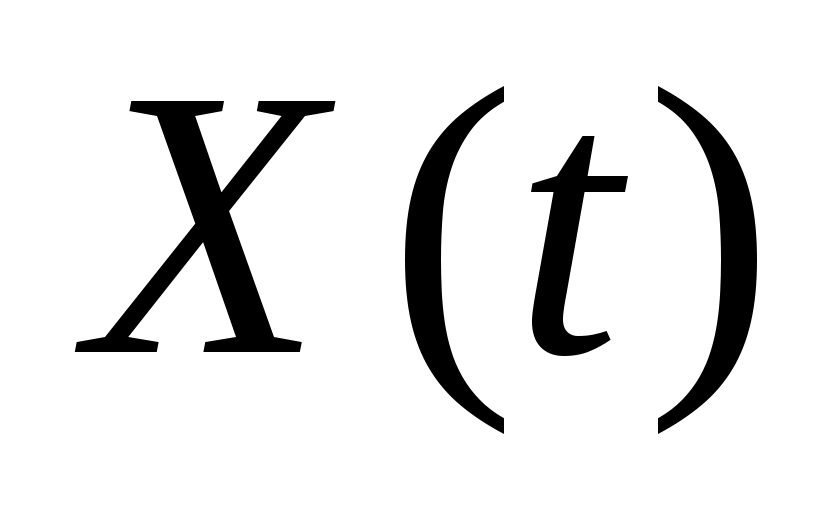 имеет спектральную плотность имеет спектральную плотность 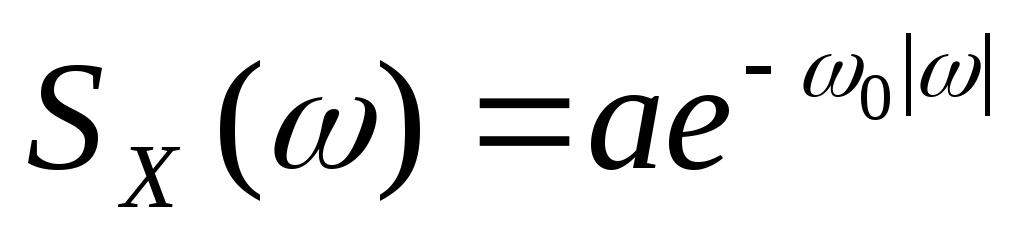 , , 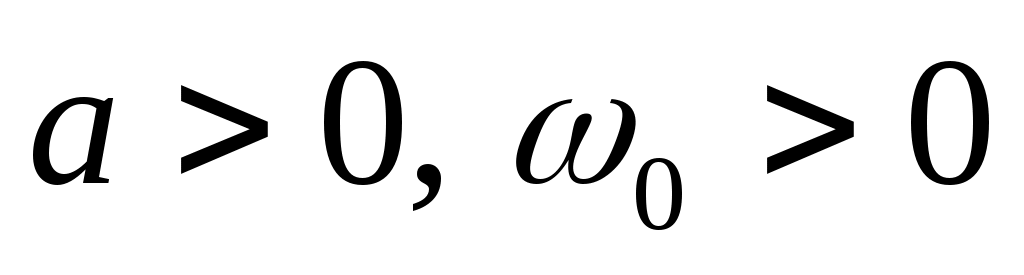 . Определить корреляционную функцию . Определить корреляционную функцию 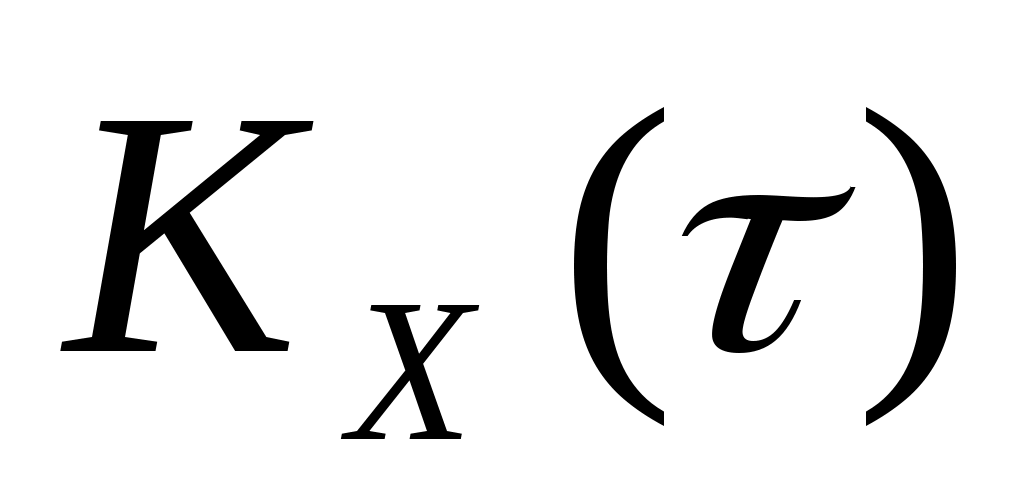 этой функции. этой функции.
5. На вход линейной динамической системы, описываемой уравнением 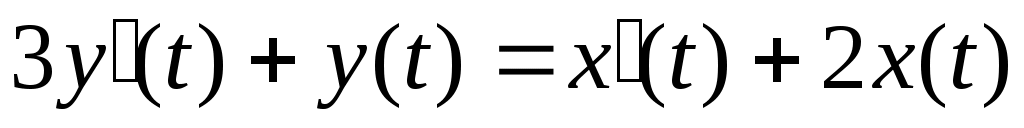 , поступает стационарный случайный процесс с характеристиками: , поступает стационарный случайный процесс с характеристиками: 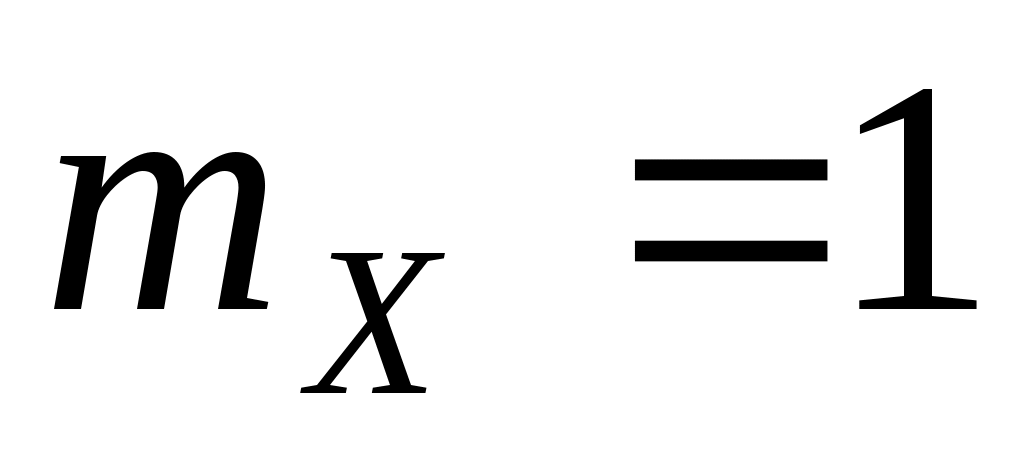 , , 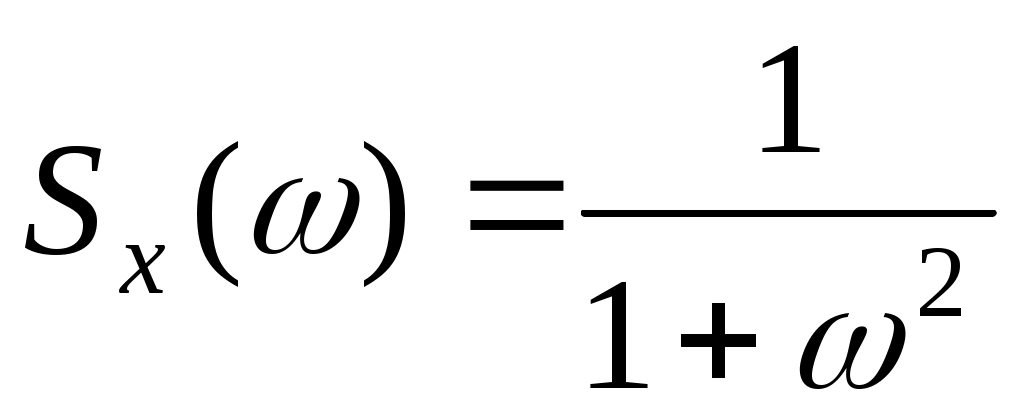 , , 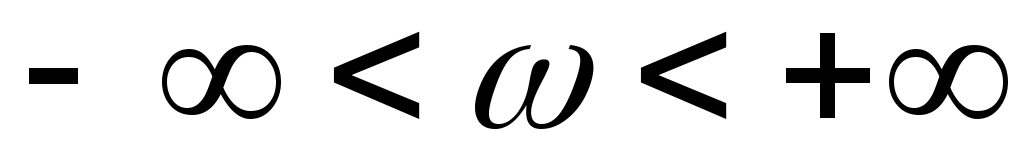 . Найти . Найти 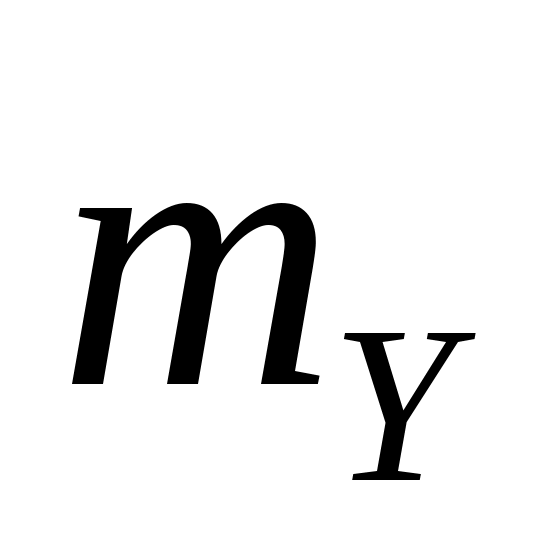 , , 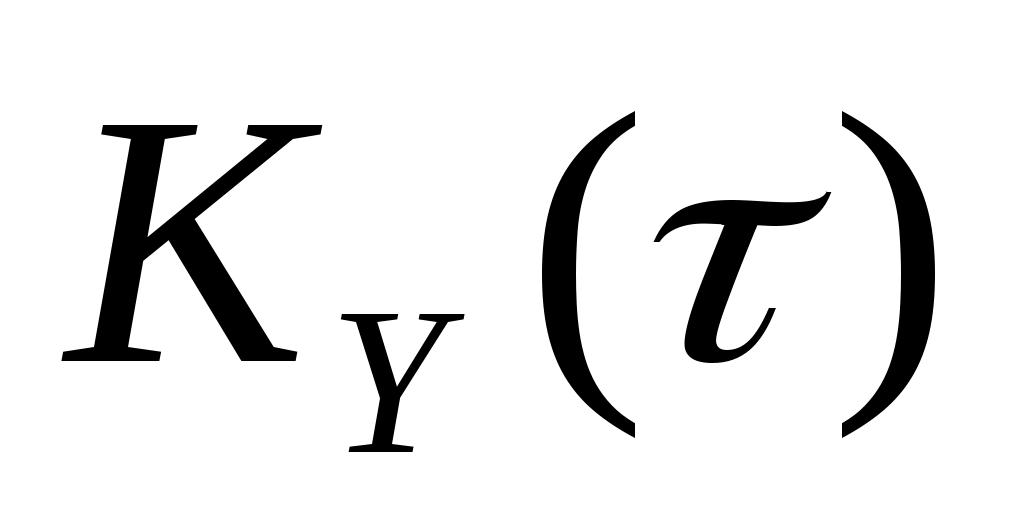 и и 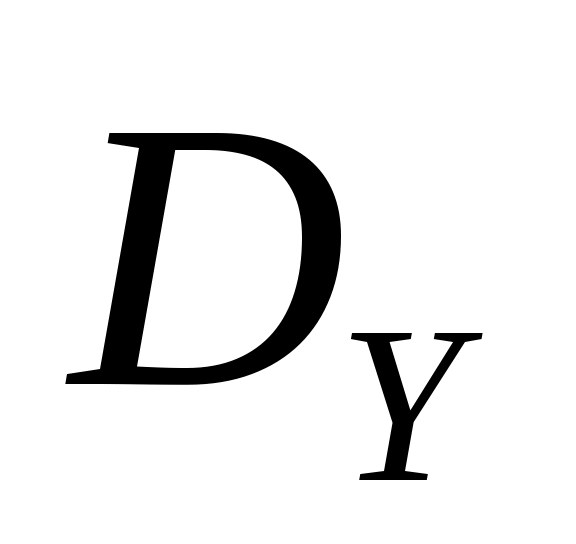 процесса процесса 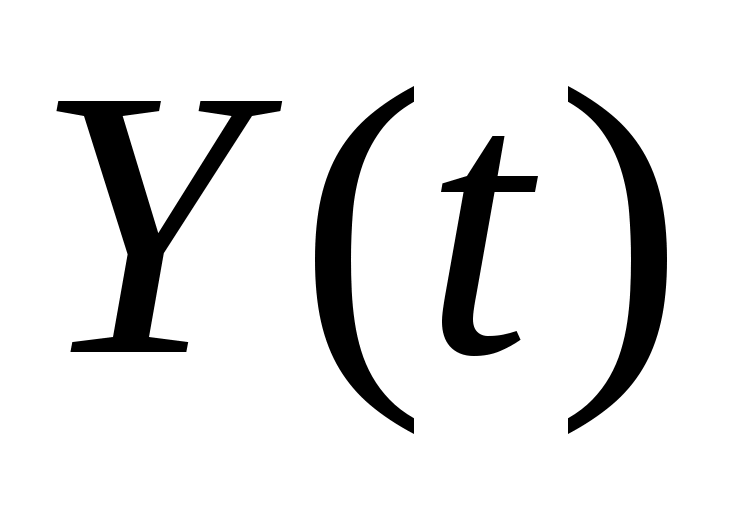 на выходе системы. на выходе системы.
К онтрольная работа № 1 онтрольная работа № 1
по дисциплине «Анализ случайных процессов»
Вариант № 14
1. Рассматривается случайная функция 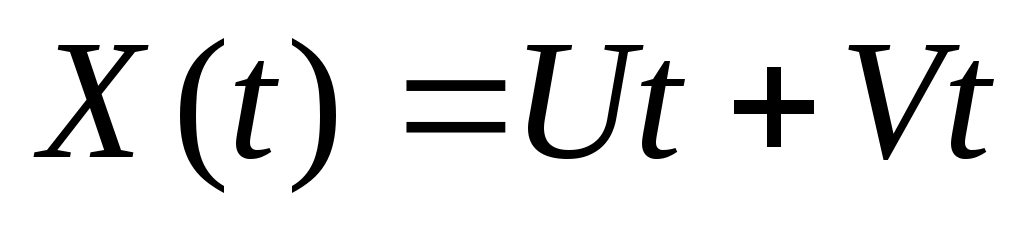 , где , где 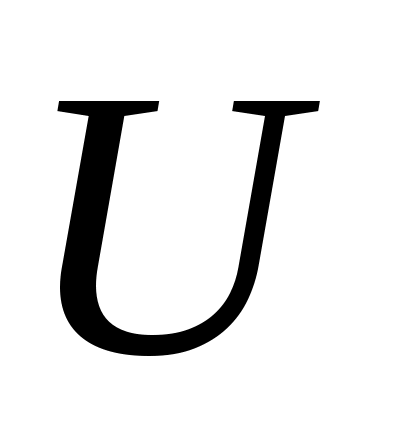 , , 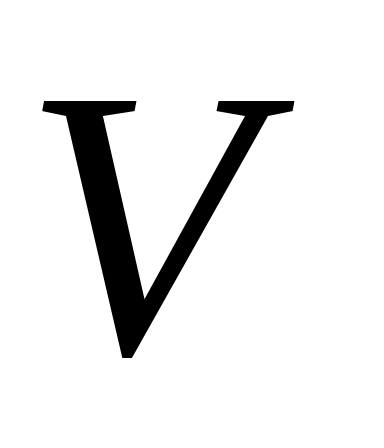 – некоррелированные случайные величины, распределенные по нормальным законам – некоррелированные случайные величины, распределенные по нормальным законам 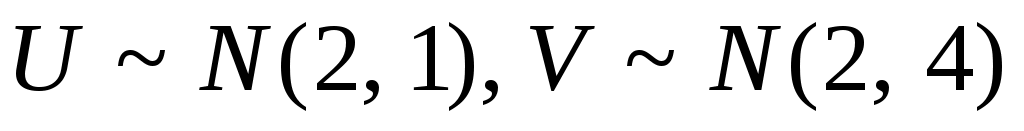 . Найти плотность распределения сечения этой функции и характеристики . Найти плотность распределения сечения этой функции и характеристики 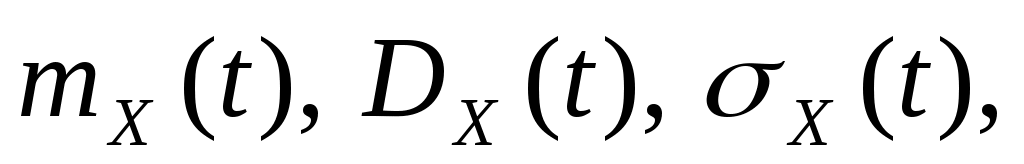 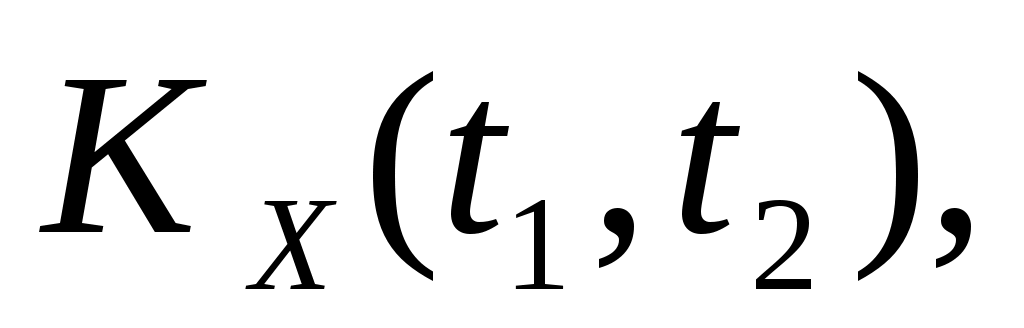 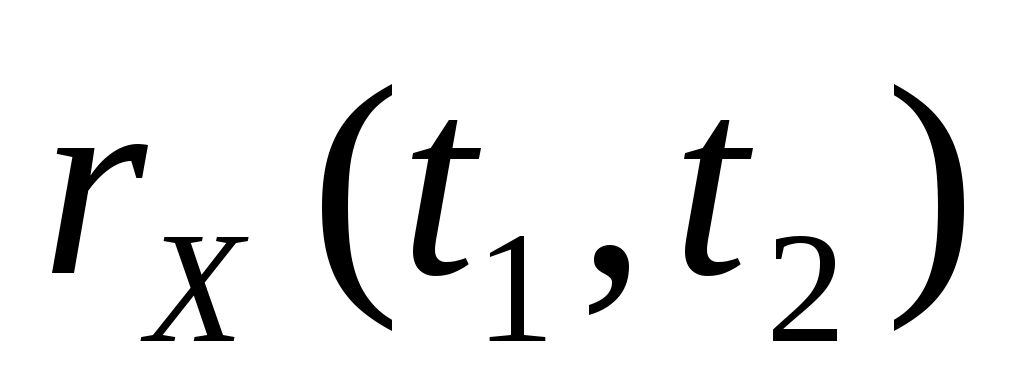 . .
2. Случайная функция |
 Скачать 1.27 Mb.
Скачать 1.27 Mb. онтрольная работа № 1
онтрольная работа № 1 онтрольная работа № 1
онтрольная работа № 1 онтрольная работа № 1
онтрольная работа № 1