|
|
лекции кристаллография. Кристаллография наука, изучающая процессы образования, формы, структуру и физикохимические свойства кристаллов
П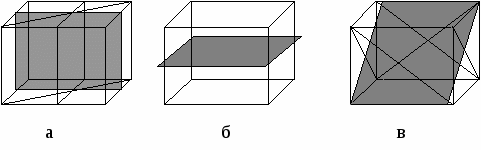 ример ример
Гексаэдр.
рис.2
У гексаэдра 9 плоскостей симметрии, из которых 6 диагональных и 3, которые проходят через середины граней и ребер, перпендикулярно им. На рис.2.а показаны 4 грани, 2 из них диагональные; на рис.2.б — одна, на рис.2.в. — 4 диагональных.
Вращение
Элемент симметрии — линия, ось вращения.
Ось симметрии — прямая линия, вокруг которой несколько раз повторяются равные части кристалла.
Теорема
Элементарный угол поворота любой оси симметрии содержится целое число раз в 3600.
=3600
n , где n — порядок оси.
n=1, =3600 (это ось первого порядка, присутствует всегда)
n=2, =1800
n=3, =1200
n=4, =900
n=6, =600
L1, L2, L3, L4, L6 — порядки осей в учебной символике.
1,2,3,4,6 — в международной символике.
В кристаллах нет осей симметрии пятого порядка, поскольку кристалл нельзя упаковать с помощью правильных пятиугольников.
Инверсия
Элемент симметрии — точка.
Центр инверсии — особая точка внутри кристалла, характеризуемая тем, что любая проведенная через нее прямая по обе стороны от нее и на равных расстояниях встречает одинаковые (соответственные) части кристалла.
Практическое указание
П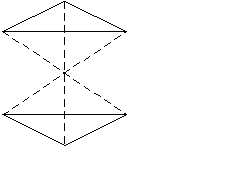 ри наличии центра симметрии каждой грани отвечает другая грань, равная и параллельная первой (рис.3) ри наличии центра симметрии каждой грани отвечает другая грань, равная и параллельная первой (рис.3)
В
А Д
С
Д1 А1
В1
Рис.3
Отражение-вращение
Элементы симметрии — зеркально-поворотные оси. Обозначение —L2nn.Зеркально-поворотная ось порядка 2n — это обычная поворотная ось порядка n.
L42 — зеркально-поворотная ось четвертого порядка.
Точку А2 можно получить двумя путями.
А А
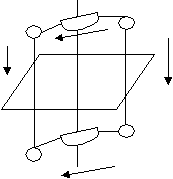 900 Ось второго порядка L21 соответств 900 Ось второго порядка L21 соответств
Р ует центру симметрии.
А1
А2 900
Рис.4
Вращение-инверсия
Учебная символика: Lin.
М еждународная — n. еждународная — n.
Н апример: Li2(2) апример: Li2(2)
Инверсионная ось — прямая линия, при повороте вокруг которой на некоторый определенный угол с последующим (или предварительным) отражением центральной точки кристалла как в центре инверсии, кристалл самосовмещается сам с собой.
П     орядки осей: Li1(1), Li2(2), Li3(3), Li4(4), Li6(6). орядки осей: Li1(1), Li2(2), Li3(3), Li4(4), Li6(6).
Самостоятельное значение имеют оси четвертого и шестого порядка, а остальные можно заменить.
Пример: Li1=С — центр инверсии.
Li2=Р — плоскость симметрии.
Li3=L3C — ось симметрии третьего порядка+центр симметрии.
Порядок оси можно определить по количеству сходящихся в одной точке ребер.
П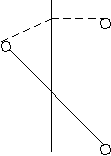 ример ример
Ось четвертого порядка.
А Ось Li4 можно заменить на L2
А1
С
L4 А2
Рис.5
Таким образом, существует 8 элементов симметрии, которые имеют самостоятельное значение:

С   (1), P(m), L2 (2), L3 (3), L4 (4), L6 (6), Li4(4), Li6(6). (1), P(m), L2 (2), L3 (3), L4 (4), L6 (6), Li4(4), Li6(6).
Сочетание восьми элементов симметрии называется формулой или видом симметрии, точечной группой. Всего их 32.
Запись вида симметрии очень строгая. Сначала указывают оси высшего порядка, потом — по убыванию, затем плоскости симметрии, и, наконец, центр симметрии. Перед каждым элементом симметрии указывают их количество. Запись сплошная, без пробелов и знаков препинания.
П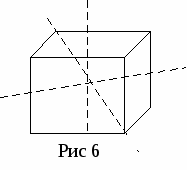 ример ример
Гексаэдр.
L3 L4 Оси симметрии 4-го порядка проходят
попарно через середины граней; оси
3-го порядка проходят попарно через вер
L2 шины; 2-го — попарно через середины
 ребер. ребер.
3L44L36L29РС
Кубы — высокосимметричные кристаллы.
Взаимодействие элементов симметрии (теоремы сложения).
2 элемента симметрии неизменно влекут за собой третий элемент (равнодействующий), действие которого равно сумме действий первых двух.
Теорема №1
Линия пересечения двух плоскостей симметрии всегда является осью симметрии, действие, которой равно сумме действий обеих плоскостей.
Э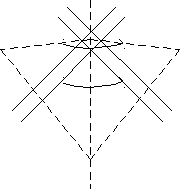 лементарный угол поворота в 2 раза больше угла между плоскостями. лементарный угол поворота в 2 раза больше угла между плоскостями.
О
А А2
n 2 m
Р1 Р2
А1
Рис.7
Обратная теорема
Действие одной поворотной оси равносильно действию двух зеркальных плоскостей, пересекающихся вдоль упомянутой оси. При этом первая плоскость проводится произвольно, а вторая плоскость должна образовывать (в направлении поворота оси) с первой плоскостью угол, равный половине элементарного угла поворотной оси.
Теорема №2
При наличии двух пересекающихся осей симметрии всегда следует искать третью равнодействующую ось, проходящую через точку пересечения первых двух (теорема Эйлера).
Лекция 3
Теорема №3
П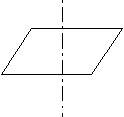 ри наличии центра инверсии и четной оси, перпендикулярно последней проходит плоскость симметрии (рис.1) ри наличии центра инверсии и четной оси, перпендикулярно последней проходит плоскость симметрии (рис.1)
С
Р
L2n
рис.1
При наличии центра инверсии и проходящей через него плоскости симметрии, перпендикулярно последней проходит четная ось симметрии (рис.1)
При наличии четной оси L2n и перпендикулярной ей плоскости симметрии всегда присутствует центр инверсии.
Следствие
При наличии центра инверсии сумма четных осей равна сумме плоскостей симметрии, причем каждая четная ось перпендикулярна плоскости симметрии.
Пример
(3+6)L2n=9P
Тетрагональная призма: L44L25РС
(4+1)L2n=5P
Теорема №3
(Следствие из теоремы Эйлера)
В присутствии осей симметрии n-го порядка и перпендикулярных к ней осей симметрии второго порядка имеем всего n осей второго порядка
Ln L2nL2
Ln PnL2, лежащих в плоскости Р.
Теорема 5
(Следствие из теоремы 1)
В присутствии осей симметрии порядка n и плоскости симметрии, проходящей параллельно этой оси, имеем всего n таких плоскостей.
Ln РnР
Понятие о единственном направлении.
Единственное не повторяющееся в кристалле направление является единичным.
Например, гексагональные пирамида(L6Р6) и призма(L66L27РС)имеют такое направление — ось L6.
Повторяющиеся в кристалле направления, сввязанные элементами симметрии, называются симметрично равными.
Пример: В кубе нет единичных направлений, все симметрично равные.
Р асположение элементов симметрии относительно единичного направления. асположение элементов симметрии относительно единичного направления.
Е В присутствии единичного направления возможен
С центр симметрии, лежащий в середине кристалла.
Е1
Рис.2
Е В присутствии оси n-го порядка, параллельной
единичному направлению, оно всегда будет
Е1Ln единичным.
Рис.3
Е Если есть ось симметрии, перпендикулярная единичн
ому направлению, то оно останется единичным.
Ln
Е1
Рис.4
Е Единичное направление останется единичным, если
есть плоскость симметрии, перпендикулярная ему.
Р
Е1
Рис.5
Е Единичное направление останется единичным, если
есть плоскость симметрии, параллельная ему
Р
Е1 Рис.6
Виды симметрии кристаллов.
В иды симметрии кристаллов, обладающих единичным направлением. иды симметрии кристаллов, обладающих единичным направлением.
Таблица I.
|
Вид симметрии
|
|
n=1
|
n=2
|
n=3
|
n=4
|
n=6
|
1. Е=Е1 Ln
|
L1 (1)
|
L2
|
L3 (9)
|
L4 (14)
|
L5 (21)
|
2. Е=Е1 С
|
L1С = С (2)
|
L2С
L2РС
|
L3С (10)
|
L4РС (15)
|
L6РС (22)
|
3. LnР
|
L1Р=Р
|
|
Li6
|
|
|
4. LnР
|
L1Р=Р (3)
|
L2 2Р (6)
|
L3 3Р (11)
|
L4 4Р (16)
|
L6 6Р (23)
|
5. Ln L2
|
L1L2=L2 (4)
|
L22L2 =3L2 (7)
|
L23L2 (12)
|
L44L2 (17)
|
L66L2 (24)
|
Присоединяются всевозможные сочетания элементов симметрии (одновременно несколько)
|
6.С,Р,параллельнаяединичному направлению.
|
L2 РС (5)
|
3L2 3РС (8)
|
L2 3L23РС (13)
|
L44L25С (18)
|
L66L27РС (25)
|
7. Единичное направление совмещено с единственной инверсионной осью n-го порядка
Е-Е1; Lin
|
|
|
|
Li4 (19)
|
Li6 (26)
|
8. К исходному единичному направлению, совпадающему с инверсионной осью n-го порядка, присоединяется плоскость, проходящая параллельно ему.
|
|
|
|
2L22Р (20)
|
Li63L23Р (27)
|
Зачеркивание штриховой линией обозначает, что этот элемент симметрии повторяется и его не нужно считать еще раз. Цифры в скобках — номер вида симметрии. Всего их 27.
Ln— порождающий элемент. Это обозначение условно, на самом деле, никаких элементов симметрии нет.
Виды симметрии — примитивные.
Плоскость симметрии появляется по теореме сложения. Виды симметрии — центральные.
Виды симметрии аналогичны центральным.
Виды симметрии — планальные
Виды симметрии — аксиальные.
Виды симметрии — планаксиальные.
Виды симметрии — инверсионно-примитивные.
Виды симметрии — инверсионно-планальные.
Виды симметрии кристаллов без единичных направлений.
Из каждого направления выводится симметрично равное.
Примитивные.
3L24L3
Центральные
3L24L33РС
Планальные
3Li44L36Р
Аксиальные
3L44L36L2
Планаксиальные.
3L44L36L29PC — куб.
Сингония — группа видов симметрии, обладающих одним или несколькими элементами симметрии (с обязательным учетом осей симметрии порядка, выше второго) при одинаковом числе единичных направлений.
С ингонии: ингонии:
Триклинная
Моноклинная I группа
Ромбическая
Тригональная (L3)
Тетрагональная (L4) II группа
Гексагональная (L6)
Кубическая III группа.
I группа: низшая категория (нет осей симметрии порядка, выше 2 –го, есть несколько единичных направлений)
II группа: средняя категория (есть одно единичное направление, совпадающее с единственной осью порядка, выше второго).
III группа: высшая категория (нет единичных направлений, все направления симметрично равные). Обязательный признак — наличие четырех осей 3-го порядка.
Лекция 4
Характеристика сингоний.
Таблица 1
Категории
|
Сингонии
|
Число единичных напрвлений
|
Характерные элементы симметрии.
|
Низшая.
|
Триклинная
|
Все
|
С
|
Моноклинная
|
Множество
|
Р, L2, L2РС
|
Ромбическая
|
Три
|
L22Р, 3L23РС
|
Средняя
|
Тригональная
|
Одно
|
L3
|
Тетрагональная
|
Одно
|
L4, Li4
|
Гексагональная
|
Одно
|
L6, Li6
|
Высшая
|
Кубическая
а=в=с
===900
|
Нет
|
4L3
|
Обозначение плоскостей и направлений в кубических кристаллах.
x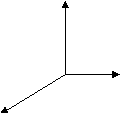 /n + y/m + z/p = 1 — это уравнение плоскости в отрезках. /n + y/m + z/p = 1 — это уравнение плоскости в отрезках.
Z
О Y
X рис.1
На рис.1 показан правильный выбор системы координат для установки кристалла.
К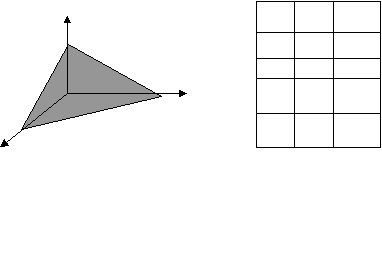 ристаллографические индексы Миллера — это наименьшие целые положительные и отрицательные числа, которые относятся между собой как величины, обратные отрезкам, отсекаемым плоскостью на координатных осях. ристаллографические индексы Миллера — это наименьшие целые положительные и отрицательные числа, которые относятся между собой как величины, обратные отрезкам, отсекаемым плоскостью на координатных осях.
Z X Y Z
1 2 4 1
½ ¼ 1
4 2/4 ¼ 4/4
Y
2 2 1 4
X
Рис.2 табл.2
Приведенное уравнение: hx + ky + lz = D. Здесь h, k, l — кристаллографические индексы.
(214) — кристаллографические индексы плоскостей, записываются в круглые скобки без знаков препинания и читаются поцифирно.
|
|
|
 Скачать 0.89 Mb.
Скачать 0.89 Mb. ингонии:
ингонии: /n + y/m + z/p = 1 — это уравнение плоскости в отрезках.
/n + y/m + z/p = 1 — это уравнение плоскости в отрезках. ристаллографические индексы Миллера — это наименьшие целые положительные и отрицательные числа, которые относятся между собой как величины, обратные отрезкам, отсекаемым плоскостью на координатных осях.
ристаллографические индексы Миллера — это наименьшие целые положительные и отрицательные числа, которые относятся между собой как величины, обратные отрезкам, отсекаемым плоскостью на координатных осях.
 ример
ример ри наличии центра симметрии каждой грани отвечает другая грань, равная и параллельная первой (рис.3)
ри наличии центра симметрии каждой грани отвечает другая грань, равная и параллельная первой (рис.3) 900 Ось второго порядка L21 соответств
900 Ось второго порядка L21 соответств еждународная — n.
еждународная — n.
 ример
ример
 ример
ример ребер.
ребер. лементарный угол поворота в 2 раза больше угла между плоскостями.
лементарный угол поворота в 2 раза больше угла между плоскостями. ри наличии центра инверсии и четной оси, перпендикулярно последней проходит плоскость симметрии (рис.1)
ри наличии центра инверсии и четной оси, перпендикулярно последней проходит плоскость симметрии (рис.1) асположение элементов симметрии относительно единичного направления.
асположение элементов симметрии относительно единичного направления. иды симметрии кристаллов, обладающих единичным направлением.
иды симметрии кристаллов, обладающих единичным направлением.