лекции кристаллография. Кристаллография наука, изучающая процессы образования, формы, структуру и физикохимические свойства кристаллов
 Скачать 0.89 Mb.
|
|
Порядок нахождения индексов плоскостей. Одинаков для кубических и гексагональных кристаллов.
Z (321) 1 0 Y 1 X рис.3 Начало координат помещают в любой узел элементарной ячейки.
Примечание 1. При выборе начала координат руководствуются тем, что плоскость должна пересекать максимальное число осей. Примечание 2: Если плоскость не пересекает оси, то ее всегда можно продолжить таким образом (или перенести параллельно самой себе), чтобы она эти оси пересекла. Пример а=в=с=1— условно равны одной осевой единице. ===900  X Y Z 1/3 ½ 1 3 2 1 табл.3 Плоскость (321). Смотреть рис.3 (h, k,l) — общая запись. ( 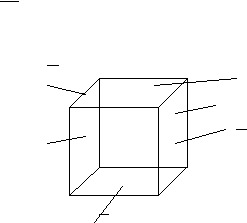 110) — такая запись означает, что есть отрицательное направление.Обозначение в скобках означает не только плоскость, но и семейство параллельных плоскостей. (010) (001) (010) (100) (100) (001) Рис.4 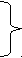 (100) (010) (001) 3 семейства. (100) (010) (001) Аспекты эквивалентности плоскостей.
{100} — совокупность эквивалентных плоскостей. При такой записи в фигурных скобках отрицательный индекс не пишется, так как подразумевается, что плоскости с отрицательными индексами входят в эту совокупность. Максимальное число плоскостей, входящих в совокупность, — 48 (если hkl); соответственно, 24 семейства. Способ подсчета всех плоскостей, входящих в совокупность. Это все возможные перестановки положительных и отрицательных индексов. П 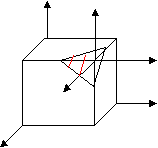 римерZ Z Если требуется определить индексы плоскости, подобной изображенной на Y рис.5, то необходимо сделать перенос  X x y z системыY -1/2 -1/2 -1/2 координат. -2 -2 -2 X рис.5 Таблица 4 Сократив на положительный множитель 2, получим: (11 1) И     ндексы направлений.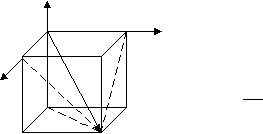 ZY X Y Z 1 1 -1 X Таблица 5 [111] Рис.6 Алгоритм определения индексов направлений.
— совокупность эквивалентных направлений. В кубических кристаллах плоскости и направления с одинаковыми индексами перпендикулярны. Определение кристаллографических индексов гексагональных кристаллов. 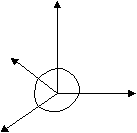 Z В системе координат есть добавочная ось U, лежащая в плоскости XY, соответствен U но появляется дополнительный индекс i. 1200 (h k i l) — плоскость. 1200 Y i = -( h+ k)— зависимый индекс. X 1200 { h k i l} — совокупность эквивалентных Рис.7 плоскостей. Максимальное число плоскостей в ней — 12, 6 семейств. Эти кристаллы менее симметричны. 12 плоскостей называются пирамидальными. 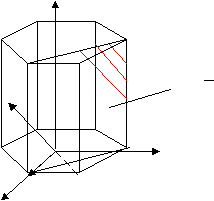 Z ПримерНачало координат можно помещать в любой узел и в центр нижней и  верхней граней. X Y U ZU (1120) а=вс 900 1 1 -1/2 =1200 1 1 -2 0 Y Условно: а=в=с=1 Таблица 6  X рис.8 (1120); i= -(1+1)= -2.Индексы направлений Возьмем направление на рис.8 Спроектирум фигуру в плоскость ХУ    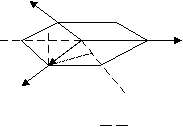U X Y U Z Y1 -1/2 -1/2 0 X 2 -1 -1 0Рис.9 Таблица 7 Направление [2110] Общая запись: [u v i w], i= -(u+v) При записи в фигурных и угловых скобках первые 3 индекса возможны с минусом, такая запись будет верна. Лекция 5 Формулы геометрической кристаллографии. Индексы – это лицо монокристалла. I. Расстояние между плоскостями, входящими в одно семейство параллельных плоскостей (hkl): d  = a/h2+k2+l2II. Определение угла между плоскостями (h1k1l1) и (h2k2l2): h1h2+k1k2+l1l2 c  os=  h1+k1+l1h2+k2+l2III. Определение принадлежности направления плоскости: (h k l) [UVW] Если hU+kV+lW=0, то направление принадлежит плоскости. Эта формула имеет практическое значение в эпитаксии. Это одно из условий протекания эпитаксии. I  V. Определение линии пересечения двух плоскостей: (h1k1l1) и (h2k2l2)h1 k1 l1 h1 k1 l1 Крайные отбрасываются, а остальные перекрестно перемножаются. h2 k2 l2 h2 k2 l2 Кристаллографические проекции. В основе метода построения кристаллографических проекций лежит закон о постоянстве углов в кристалле. I. Сферические координаты. Определяются две координаты и . Сферические проекции можно получить: 1. Если две грани путем параллельного переноса свести в одну точку – центр сферы проекции и продолжить до пересечения со сферой. С 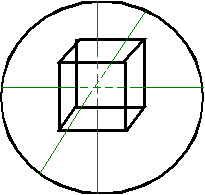 ферическая проекция – это совокупность точек на сфере. Этот комплекс называется планарным комплексом (все грани в одну точку).2. Если к каждой грани построить перпендикуляр и продлить его до пересечения со сферй, то мы полу- чим совокупность точек на сфере. Совокупность называется поляр- ным комплексом. 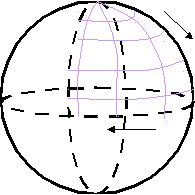 N На поверхность шара наносится вспо-могательная сетка. -долгота, один из меридианов нулевой Долгота определяет угол между нуле- вым меридианом и меридианом, опре- деляющим пл-ть (по часовой стрелке). O Вторая координата, - полярное рас- стояние, называется расстояние, заклю- ченное между полюсом и соответствую- щей точкой; отсчитывается по меридиа- S ну, проходящему через полюс и данную точку. Существует несколько сеток. Сетка Вульфа: ее диаметр 20 см цена деления 20 Недостаток метода сферических проекций заключается в объемности. II. Стереографические проекции.   N  A1 A   O  A2 Q  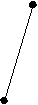 Для их построения действуют аналогично сферическим координатам. Есть точка, описываем ее сферой произвольного радиуса. Через центр сферы проводят плоскость Q-плоскость проекции. В результате пересечения плоскости со сферой имеем большой круг проекции. S – «точка зрения» Направление ОА продляем до пересечения со сферой. Затем соединяем А1 с «точкой зрения». Точка А2 –стереографическая проекция направления ОА. SA1 – луч зрения Если направление под лучом к плоскости проекции, то это будет точка внутри круга проекции. Если направление перпендикулярно плоскости проекции, это точка в центре круга проекции (т. О). Если же направление параллельно плоскости проекции, то это две точки на круге проекции.  под углом к плоскости перпендикулярно параллельно плоскости проекции плоскости проекции проекции На стереографических проекциях оси симметрии обозначаются следующим образом: L 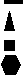 2L3 L4 L6 П  лоскость проекции обозначается (Р): Центр проекции (С): С О 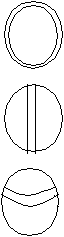 бозначение плоскостей:Если плоскость параллельна основному кругу проекции. Плоскость перпендикулярна плоскости проекции. Дуга, если плоскость расположена под углом. Рассмотрим обозначение осей, плоскостей симметрии на примере КУБА Пример. 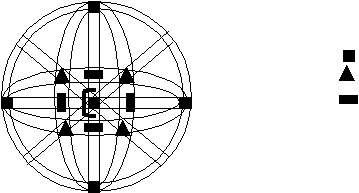 L4(001) В кубе: 3L4 - 4L3 - 6L2 - 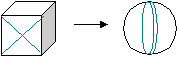 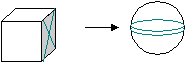 Ш. Гномостереографические проекции. Берется кристалл, строится его полярный комплекс и этот комплекс проецируется на плоскость проекции. За центр тяжести многогранника принимается цент сферы (произвольного радиуса). Через точку О приводим горизонтальную плоскость Q и все условимся обозначать на этой плоскости. N     n       b a a=a1b=b1     Q b1 c a1 dd1 d=d1 m c d1S b1 a1 Горизонтальные грани проецируются в центр круга проекций. Вертикальные (d1) находятся на самом круге проекций. Косые грани внутри круга проекций. I 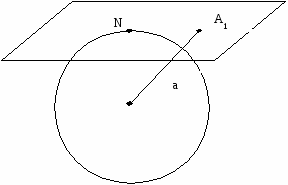 V. Гномонические проекции.(используется в ренгено-структуром анализе) Плоскостью проекции является ка- сательная к северному полюсу. Гномонические проекции плос- костей – точка. Гномоническая проекция направле- ния – прямая. Недостаток: При построении проекций не сохраняются угловые соотношения, но координаты точек на гномонической проекции прямо пропорциональны индексам Миллера. Лекция 6 Решетки Бравэ В 1848 году О.Бравэ вывел 14 типов решеток Бравэ. Условия выбора элементарного параллелепипеда повторяемости.
Ребра параллелепипеда повторяемости совпадают с элементарными трансляциями в решетке. Теорема. В решетке всегда имеются трансляции, параллельные осям и плоскостям симметрии, а также трансляции, перпендикулярные к упомянутым элементам симметрии.
Таблица 1
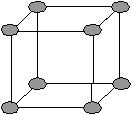
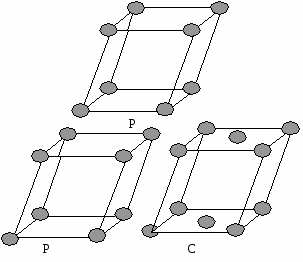
В  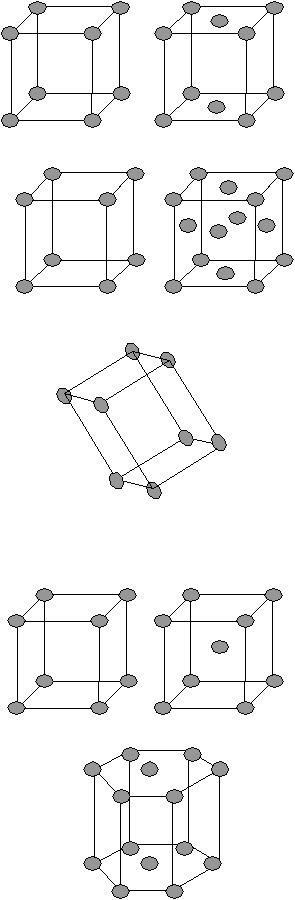 сего к низшей категории относится 7 типов решетки.
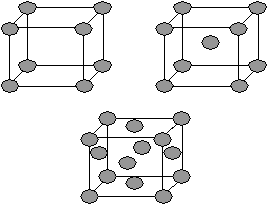
В средней категории 4 типа решеток Бравэ.
К высшей категории относится 3 типа решеток Бравэ. Совокупность координат узлов, входящих в элементарную ячейку, называют базисом ячейки. Симметрия внутреннего строения. Для внешней формы, как упоминалось раньше, существует 8 независимых элементов симметрии. Для внутреннего строения добавляются следующие симметрические операции:
Элементы симметрии — узел, ряд, сетка.
Элементы симметрии — плоскости скользящего отражения. Всего их 5: a, b, c, n, d.
Элементы симметрии — винтовые оси (двойные, тройные, четверные, шестерные). Эти симметрические операции вводятся для бесконечных фигур. П  лоскость скользящего отражения.а рис.1 Если скользящее отражение происходит вдоль оси Х, то это плоскость а, по оси У — в, по оси Z — с. Пример для типа а 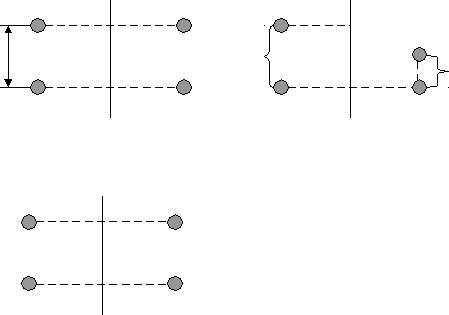 ОХТ Т t=½Т Р а а) б) Рис.2 Пример для типа с ½ ½ —поднятие происходит на эту высоту. С Эти плоскости обладают поступаниями (компонентами скольжения), действующими параллельно кристаллографическим осям. П 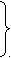 о осям: Х — ½ аУ — ½ в величины поступаний, где а, в, с — элементарные Z — ½ c трансляции или типы плоскостей. У плоскоcтей n и d компоненты скольжения (поступания) направлены по диагоналям сторон элементарной ячейки и равны их половинам и четвертям. Для n: ½ (а+в) Для d: ¼ (а+в) ½ (в+с) ¼ (в+с) ½ (а+с) ¼ (а+с) Пример NaCl — поваренная соль. 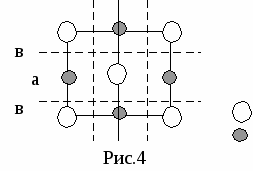 в(100) а=в — Cl а Р а — Na Здесь плоскости скользящего отражения чередуются с обыкновенными плоскостями симметрии. Винтовые оси =3600/n — одинарные. 21 — двойные (поворот на 1800 и подъем на ½ элементарной трансляции). 31, 32 — тройные (поворот на 1200 и поворот на 1/3 или 2/3 элементарной трансляции). 41, 42, 43 — четверные. 61, 62, 63, 64, 65 — шестерные. Подстрочный индекс: t=T/n, где T — величина трансляции, n — порядок оси. Винтовые оси бывают левые и правые, либо и левые, и правые одновременно. Пример 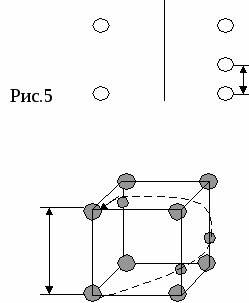 ½ Т 2 Тетрагональные кристаллы 5 4 Т 3 2 1 рис.6 Это четверная правая ось 41 (поступание ¼ ), поскольку закручивание идет по часовой стрелке, если смотреть снизу . Если закручивание идет против часовой стрелки, если смотреть снизу , то ось левая. К  омбинируя восьми элементов симметрии внешней формы конечных фигур и элементов симметрии внутренней формы бесконечных фигур, получаем 230 пространственных групп (32 точечные группы 230 пространственных групп).Пространственная группа — совокупность всех элементов симметрии кристаллической структуры. Понятие о пространственной системе точек Любая точка, повторенная элементами симметрии пространственной группы, приводит к правильной системе точек. Правильной системой точек называется система точек, выводящихся из исходной точки посредством элементов симметрии пространственных групп. Правильная система точек для каждой пространственной группы выражает геометрические законы пространственного расположения структурных единиц в кристалле. Лекция 7 Место нахождения исходной точки это ее позиция. Число точек системы, приходящихся на одну элементарную систему, называется кратностью системы. Если точка не находится не на одном из закрытых элементов симметрии, ее позиция называется общей. Если же находится – частной. Кратность частной меньше в целое число раз общей позиции. 230 пространственных групп симметрии. Пространственной группой называется сочетание всех возможных преобразований симметрии в кристаллической структуре. Каждой точечной группе соответствует несколько пространственных групп. В 1890-1894 гг. Федоров, Шенфлис вывели 230 пространственных групп. |
становить начало координат.
