лекции кристаллография. Кристаллография наука, изучающая процессы образования, формы, структуру и физикохимические свойства кристаллов
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
+ Две сферы, разделенных плос- костью антисимметрии (плос- кость меняет знак на противопо- ложный) - m    m m - Если использовать антисимметрию: Если было 32 точечные группы, то будет 58. Эффект, обратный пироэлектрическому – электрокалорический – действие электрического поля вызывает изменение температуры кристалла и фиксируется с точностью 10-9 0С. Физические свойства кристаллов, описываемых тензором второго ранга.
Рассмотрим тензор второго ранга на примере закона Ома для изотропной среды: j=E, где -удельная проводимость, а j и E - вектора. Для определения нужно определить 9 независимых компонент. Каждая компонента плотности тока линейно зависит от трех компонент направленности поля. j1=11E1+12E2+13E3 j2=21E1+22E2+23E3 j3=31E1+32E2+33E3 Для того чтобы определить удельную проводимость в кристалле нужно определить 9 независимых компонент.   11 12 13 11 12 13ij= 21 22 23 31 32 33 Значения коэффициентов 11,22,33 зависят от выбранной системы координат. Удельная проводимость описывается теннзором второго ранга. Если ij=ji, то число компонент тензора сокращается до 6. Для того чтобы наглядно описать это свойство строят указательную поверхность. Указательная поверхность удельной проводимости записывается уравнением: 11X12 +22X22 +33X32 +212X1X2 +213X1X3 +223X2X3 =1 В тензоре второго ранга всегда определяют главные оси. Главные оси в кристалле – это те направления, вдоль которых вектор воздействия и вектор возникающего явления, совпадают по направлению. Главные оси симметрии тензора второго ранга это три взаимно перпендикулярных направления, при выборе которых за координатные оси общее уравнение принимает следующий вид: S11X12 + S22X22 + S33X32 =1 Если S11, S22, S33 >0, то поверхность – эллипсоид. Если два коэффициента >0, а один <0, то поверхность однополосный гиперболоид. Если один коэффициент >0, а два <0, то характерная поверхность – двух полосный гиперболоид. В применимости к …   11X12 +22X22 +33X32 =1 11 0 0 11X12 +22X22 +33X32 =1 11 0 0Тензор второго ранга будет иметь диагональный вид: 0 22 0 0 0 33 j1=11E1 j2=22E2 j3=33E3 Геометрические свойства указательной поверхности.
(*) – совпадает с осями симметрии 2-го порядка. (**) – совпадает с осью трехосного эллипсоида вращения. Е Sij=Sji сли в триклинной сингонии тензор центрально-симметричен, то Кристаллы всех классов симметрии могут обладать свойством, описываемым тензором второго ранга. Лекция 16 Оптические свойства кристаллов Двупреломление лучей Оно характерно для кристаллов низшей и средней категории. К — кристалл  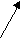 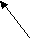 М L DМ, DL — 2 образо М L DМ, DL — 2 образо K вавшихся луча, плос K вавшихся луча, плос  D кости их колебаний D кости их колебанийвзаимно перпендику лярны. зложение луча при преломлении на 2 луча называется двупреломлением. В кальците CaCO3 угол расхождения лучей 6,50. Это свойство связано с анизотропией кристаллов. Кубические кристаллы оптически изотропны. Для них характерна поверхность световых волн в форме шара и показатель преломления n один для всего кристалла. Для кристаллов средней и низшей категории поверхности световых волн состоят из вставленных друг в друга шара и эллипсоида. 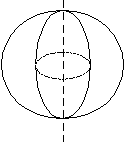 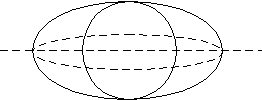              главная ось главная ось
—   отрицательный кристалл отрицательный кристаллКристаллы средней категории имеют одну оптическую ось. Обыкновенный луч — волновая поверхность отвечает шару, луч распространяется во все стороны с одинаковой скоростью. Необыкновенный луч — волновая поверхность отвечает эллипсоиду, в разных направлениях скорость различна. Для кристаллов низшей категории волновая поверхность имеет более сложный вид. В практической кристаллографии пользуются особыми волновыми поверхностями, которые называются оптическими индикатриссами. Это указательная поверхность тензора диэлектрической непроницаемости (ij). С ее помощью можно определить:
Соответственно возникает 3 показателя преломления.    ng ng    np npnm  + nm = np + nm = npОптическая ось — направление, по которому не происходит двупреломление света. ng — максимальный np — средний nm — минимальный Д   аже если кристалл ориентирован по-другому, ng все равно направлен вдоль главной оси. аже если кристалл ориентирован по-другому, ng все равно направлен вдоль главной оси.np   nm ng nm ng - -В эллипсоиде вращения все перпендикулярные оси сечения являются кругами. (nm = np) В средних кристаллах вдоль главной оси (L6, L4, L3) идет неполяризованный и нераздвоенный луч.     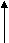       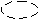 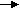 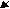 L6 Кристаллы средней категории имеют одну оптическую ось (одноосные). Их оптическая индикатрисса ограничена двумя величинами:
Величина двупреломления: ng -np. Для кристаллов низшей категории оптическая индикатрисса — эллипсоид с тремя неравными взаимно перпендикулярными осями и каждая ось — единичное направление. Эти кристаллы оптически двуосны, значит, чтобы определить n в кристаллах низшей категории, надо определить 3 показателя преломления (ng, np, nm). Оптическая индикатрисса ограничена тремя величинами: Ng, Np, Nm. Величина двупреломления та же: ng -np. Дефекты в кристаллических материалах Классификация дефектов Проводится по размерному признаку.
Это дефекты, которые соизмеримы с размерами атомов в трех измерениях. Виды:
Имеют размеры, соизмеримые в двух измерениях с размерами атома, а в третьем — с размерами кристалла.
В двух измерениях соизмеримы с размерами кристалла, а в третьем — с размерами атома.
В трех измерениях соизмеримы с размерами кристалла (макроскопические дефекты)
Дефекты оказывают влияние на следующие свойства:
Источники дефектов:
Точечные дефекты Кроме простых, к ним относятся дефект Шотки и дефект Френкеля (сложные дефекты). Вакансии Могут находится в любых узлах решетки. Рассмотрим плоскость (100) в ГЦК решетке.         Штрих пунктиром обозначено отсутствие атома. Происходит искажение кристаллической решетки, в первом приближении точечный дефект вакансия — центр сжатия в упругой среде. Упругие смещения атомов убывают обратно пропорционально кубу расстояния от центра дефекта (1/r3). Это все в предположении, что кристалл — упругая сплошная среда. 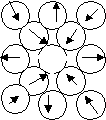   <110> <110>  <100> <100> Атомы первого слоя испытывают подвижку в сторону вакансии на 0,84% от а. Атомы второго слоя испытывают подвижку в обратную сторону из-за выталкивания атомами первого слоя на 0,25% от а. Атомы третьего слоя испытывают подвижку в ту же сторону, что и на 0,03% от а. Поле смещений вокруг вакансии сильно анизотропно. Межузельный атом (  110) 110)ГЦК 20% от а. Поле смещений анизотропно, механизм тот же. Для металлов Vвак 0,6Vат (Vвак 0,05-0,6Vат) Для полупроводников Vвак 0,8Vат Точечные дефекты повышают энергию кристалла. Энергия упругой деформации решетки составляет сотые доли электронвольта, ее вклад в общую энергию очень мал. Основная доля энергии образования точечного дефекта связана с нарушением периодичности атомной структуры и сил связи между атомами. Для металлов (Cu) Еv 1эВ Для полупроводников (Si и Ge) происходит разрыв четырех связей, энергия каждой связи 0,5 эВ, Еv 2эВ. Межузельные атомы могут быть собственными (самовнедрения, внедряется из этого же кристалла)           |

