лекции кристаллография. Кристаллография наука, изучающая процессы образования, формы, структуру и физикохимические свойства кристаллов
 Скачать 0.89 Mb.
|
неустойчивая устойчиваямодификация модификация ZnSвюрцит сфалерит (монотропный процесс) 95,50С сера ромбиическая сера моноклинная (энатиотропный пр-сс) 5730С -кварц-кварц (энатиотропный пр-сс) Скорость полиморфного перехода зависит от температуры. При температурах несколько ниже температуры превращения скорость перехода устойчивой при высокой температуре формы, возрастает постепенно достигая максимума. Из двух полиморфных модификаций устойчивой является форма с наименьшим давлением пара при данной температуре. Переход из одной полиморфной модификации в другую всегда осуществляется при определенном соотношении температуры и давления. На образование различных полиморфных модификаций влияют также: химический состав раствора, из которого происходит криталлизация, и наличие в нем примесей, не считая давления и температуры. Когда осуществляется полиморфное превращение, менется тип химической связи. Полиморфные превращения с незначительным перемещением ионов, атомов и молекул называются сдвиговымипревращениями в отличие от реконструктивных превращений, связанных с возникновением совершенно новой структуры. Если образуются структуры с разными координационными числами, то существует правило: При низких температурах и высоких давлениях устойчивой является форма с большим координационным числом. Наоборот, при высоких температурах и нормальном давлении устойчива форма с меньшим координационным числом. Возможны отклонения от правила. ПК ОЦК ГЦК К6 К8 К12 =0,52 =0,68 =0,74 При увеличении давления и уменьшения температуры идет изменение структурного типа. ZnS NaCl CsCl Понижение давления и увеличение температуры связано с образованием менее плотной упаковки. CsCl NaCl ZnS К8 К6 К4 Для полиморфных модификаций в некоторых случаях полиморфный переход связан с вращением группы атомов в кристаллической структуре, которое начинается после достижения определенной температуры. Классификация полиморфных модификаций по Бюргеру
RbCl
Вюрцит Сфалерит
-кварц -кварц
CuAg П 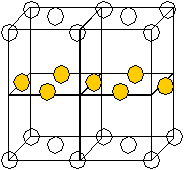 ри Т <4080 — упорядоченная структура.
Политипия — структуры, построенные из одних и тех же слоев с разной последовательностью их чередования. Понятие используется для плотно упакованных и слоистых структур. Пример: SiC. а и в в слое сохраняются, а с изменяется. Полиморфизм Fe. -Fe, -Fe, -Fe, -Fe. , , — ОЦК, но параметры решетки отличаются. — ГЦК При этом изменяются и физические свойства. -Fe -Fe — изменяются и магнитные свойства. -Fe -Fe — увеличивается плотность и уменьшается объем. Магнитными (изоструктурными) называются кристаллы, имеющие один и тот же тип кристаллической структуры. AIIIBV — сфалерит. Гомеотипия —сопоставляемые структуры не имеют полного подобия, характерного для изотипных структур. Пример: Алмаз — сфалерит. Особый случай гомеотипии — антиизоморфизм: разные соединения имеют один и тот же тип кристаллической структуры, но позиции катионов заняты анионами и наоборот. CaF2 — F Li2O, Na2O — Li или Na Изоморфизм — явление наличия у различных соединений одинакого внешнего огранения при почти равных углах между гранями (изогонизм). Причина изоморфизма — изоструктурность Классификация изоструктурных соединений пр Гримму.
Лекция 14 Кристаллофизика Это раздел кристаллографии, посвященный изучению физических свойств. Задача кристаллофизики — установление общих закономерностей в зависимости от строения (симметрии) физических свойств кристаллов. Предельные группы симметрии (группы Кюри) Это точечные группы, которые содержат ось симметрии бесконечного порядка (L). Всего их семь.
 L, группа энантиоморфна (один конус можно получить из другого путем отражения в плоскости), полярна (основание конуса и его вершина физически различны). Это предельная группа для точечных групп с осями симметрии 2, 3, 4, 6 порядков.
+ Е - LР, полярна, отражает симметрию однородного электрического поля, поперечных элементов симметрии нет.
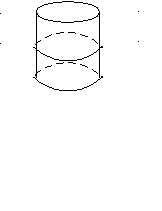 LРС, полярна, торцы цилиндра неодинаковы (вращаются в разные стороны, если смотреть сверху и снизу). Это симметрия постоянного магнита и магнитного поля постоянного тока.
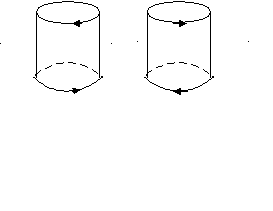 LL2, группа энантиоморфна, если смотреть сверху (снизу), вращение идет в одну сторону, это симметрия вращения плоскости поляризации в анизотропной среде.
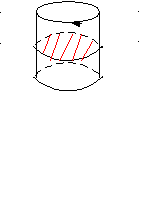 L LL2( +1)PC, отражает симметрию одноосного растяжения (сжатия), это предельная группа для точечных групп с одной осью 2, 3, 4, 6 порядка, плоскостями вдоль и перпендикулярно этой оси.
LPС. Симметрия гидростатического всестороннего сжатия или однородного нагрева.
L. Это симметрия удельного вращения плоскости поляризации в изотропной среде, группа энантиоморфна. Влияние симметрии на все физические явления определяется общим принципом симметрии Кюри: Если определенные причины вызывают соответствующие следствия, то элементы симметрии причин должны проявляться в вызванных ими следствиях. Если в каких-либо явлениях обнаруживается определенная дисимметрия, то она должна проявляться и в причинах, их породивших. Дисимметрия — отсутствие каких-либо элементов симметрии. В этом принципе нет обратного хода. Он применим ко всем физическим явлениям, в которых проявляется симметрия. В применении к кристаллам это означает, что элементы симметрии кристаллов являются в то же время и элементами симметрии любого физического свойства. Это основной закон кристаллографии (принцип Нейнмана): Физическое свойство кристалла может обладать и более высокой симметрией, чем кристалл, но оно должно обязательно включать у в себя симметрию кристалла. Принцип суперпозиции Кюри Если различные внешние явления или воздействия накладываются друг на друга, образуя единую систему, то их дисимметрии складываются и остаются лишь общие элементы симметрии. Пример Куб Было: 3L44L36L29PC Воздействие: LР    L L3       L2  L4 [001] Результирующая симметрия будет разная, в зависимости от того, вдоль какой оси приложено воздействие, в данном случае, L4 Стало: L44Р, остальные элементы симметрии исчезли. Стереографическая проекция результата 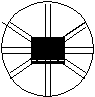 Указательная поверхность Для наглядного представления симметрии и анизотропии свойства пользуются указательной поверхностью, радиус-векторы которой характеризуют относительные величины свойства в данном направлении. Для построения указательной поверхности:
Симметрия физического свойства, а, следовательно, и указательной поверхности, может быть выше, чем симметрия кристалла (принцип Нейнмана), но при этом симметрия указательной поверхности должна содержать в себе симметрию кристалла. Системы координат В 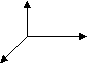 кристаллографии: zy х Углы любые В кристаллофизике: х3х2 х1 Всегда правая и ортогональная Они совпадают для кубических, ромбических и тетрагональных кристаллов. Одно и то же явление может быть выражено различными уравнениями, вид которых зависит от системы координат. При этом всегда надо знать, как преобразуется физическое свойство при переходе от одной системы координат к другой. В  следствие анизотропии свойств кристаллов явление, вызванное в кристалле каким-либо воздействием, может не совпадать по направлению с этим воздействием, поэтому взаимосвязь свойства, воздействия и явления выражаются уравнением:явление(эффект)=свойство*воздействие (1) Лекция 15 Скалярные и векторные свойства кристаллов. Скалярное свойство не зависит от направления, изотропно, обладает максимальной симметрией, и указательная поверхность скалярного свойства это сфера.
Векторные свойства зависят от направления. явление = свойство*воздействие Определяются по координатам X1, X2, X3. Пусть у нас стоит задача осуществить переход к новой системе координат. 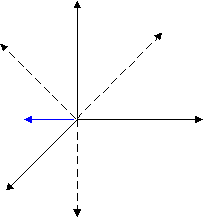 X3X’2 X’3 A X2 X1 X’1 A – вектор в координатах X1, X2, X3. При переходе из одной системы координат в другую (X1, X2, X3X’1, X’2, X’3) скалярные свойства не меняются. явление = свойство*воздействие (вектор) (вектор) (скаляр) Свойство определяется компонентами вектора по трем осям или тензором первого ранга. 31=3 3р, где р – ранг тензора – число компонент. 32=9; 33=27. При переходе X1, X2, X3X’1, X’2, X’3 ( повернутой на угол ) нужно преобразовать векторную велечину по закону косинуса и это имеет вид: А  ’i=cikAkAk=(A1,A2,A3); i,k=1,2,3… cik - косинус между старой и новой системой координат: сik=cos(X’i Xk) i – относится к новой системе координат, а к – к старой. A’1=A1cos(X’1X1) + A2cos(X’1X2) + A3cos(X’1X3) = c11A1+c12A2+c13A3 Это равенство можно представить в виде таблицы косинусов.
По этой таблице определяются коэффициенты при переходе от одной системе к другой. Для изучения физического свойства кристалла сначала устанавливают изотропно или анизотропно свойство. Если свойство анизотропно, то надо установить ранг тензора и его связь с симметрией кристалла. Компоненты тензора определяются по матричной формуле. Если у нас 32=9 – это обычный вектор, который определяется девятью фактическими компонентами (их нужно определить). Компоненты тензора второго ранга aij определяются:   a11 a12 a13aij= a21 a22 a23 32=9 a31 a32 a33 Пироэлектрический эффект – это явление, которое присуще и состоит в способности изменять величину явление = свойство*воздействие При нагревании или охлаждении кристаллов на его гранях появляется заряд противоположных знаков. 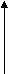  n ps ps – вектор спонтанной поляризации.   =Р2i*ni = |P2|cos,  n – единичный вектор;  При равномерном распределении температуры происходит изменение вектора спонтанной поляризации, который определяется величиной коэффициента - вектор пироэлектрических коэффициентов. 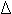 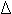рs= T (1,2,3) - положителен, если возрастание температуры приводит к возрастанию спонтанной поляризации. Пироэлектрический эффект может наблюдаться не во всех кристаллах, а только в кристаллах десяти классов, у которых есть единичное направление. Указательная поверхность пироэлектрического эффекта:  |
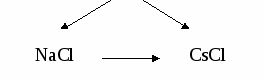ревращение с изменением координационного числа.
g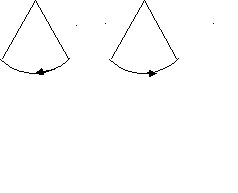
ращающиеся в разные стороны конусы.
окоящийся конус
ращающийся цилиндр
окоящийся цилиндр
окоящийся шар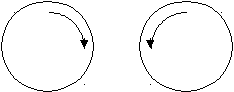
ращающийся влево или вправо шар