Курс лекций НЭ_ч4-ч5_Богач_2013. Курс лекций " Основы наноэлектроники"

• Название: Курс лекций " Основы наноэлектроники"
• Анкор: Курс лекций НЭ_ч4-ч5_Богач_2013.doc
• Дата: 26.04.2018
• Размер: 3.44 Mb.
• Имя файла: Курс лекций НЭ_ч4-ч5_Богач_2013.doc
• Тип: Курс лекций; #18523
• страница: 16 из 17

5.6.Эллипсометрия.

Одним из наиболее прецизионных методов определения тол­щины пленок, прозрачных для оптического излучения, является эллипсометрия, впервые предложенная и реализованная П.Друдэ в 1887 г. Исследования П.Друдэ отражения света от поверхности с тонкой и геометрически плоской пленкой стали классическим образцом в эллипсометрии. Поскольку столь прецизионные ис­следования и измерения толщин пленок не были востребованы, интерес к эллипсометрии не проявлялся. Однако в последнее вре­мя он существенно повысился со стороны специалистов, работа­ющих в области физики поверхностных явлений, физики тонких пленок, пленочных полупроводниковых схем, физики полупро­водников, диэлектрических, полупроводниковых и металлических покрытий, электрохимии и коррозии металлов, адгезии и адсор­бции полимеров.

Это обусловлено тем, что в указанных областях эллипсометрия обладает существенными (а иногда и уникальными) преимуще­ствами перед другими методами, поскольку для исследования свойств тонких пленок и граничных слоев этот поляризационно­оптический метод не требует специальной подготовки поверхно­сти (т.е. не вносит артефактов), позволяет вести наблюдения за поверхностями при различных физических условиях (температу­ры, давления), в частности при контакте их с жидкостями.

Особый практический интерес представляет возможность изу­чения кинетики быстропротекающих процессов на границах раз­дела (кинетика образования поверхностных покрытий, роста пле­нок, кинетика кристаллизации и т.д.). Для этой цели разрабатываются автоматические эллипсометры с использованием электро- и магнитооптических элементов.

Термин «эллипсометрия» предложил в 1944 г. А. Ротен, посколь­ку речь идет об изучении эллиптической поляризации. Хотя ука­занные изменения можно наблюдать как в отраженном, так и в проходящем свете, в настоящее время в подавляющем числе ра­бот изучается поляризация отраженного света. Поэтому обычно под эллипсометрией подразумевают изучение изменений поляри­зации света вследствие отражения. В тех случаях, когда это воз­можно, эллипсометрия в проходящем свете удачно дополняет эллипсометрию в отраженном свете и даже может служить основ­ным методом исследования в случаях, когда измерения отражен­ного акта затруднительны (например, при слабом отражении от диэлектриков).

Классическая эллипсометрия занимается измерением оптиче­ских постоянных и толщины поверхностных пленок с резкими гра­ницами раздела между фазами. Однако реальные поверхности ха­рактеризуются переходными слоями с плавным изменением ис­следуемых локальных свойств и трудности математического описа­ния механизма отражения света от такой границы в большинстве случаев вынуждают принять более простую модель переходного слоя, характеризуемую с помощью некоторых эффективных параметров. Это выводит за рамки исследования такие параметры реальной по­верхности, как шероховатость, неоднородность, анизотропия и т.д.

Эллипсометр представляет собой поляризационный гониометр, на подвижных плечах которого расположены поляризационные элементы: поляризатор, анализатор, компенсатор, источник све­та и фотодетектор (рис. 7.27). Лимб гониометра обеспечивает уста­новку заданного угла падения, а поляризационные элементы по­мещаются в собственные лимбы и могут свободно вращаться.

Источник света должен обеспечивать получение рабочего све­тового пучка с высокой степенью монохроматичности и узкой диаграммой направленности для того, чтобы можно было считать волновой фронт плоским. В качестве поляризатора и анализатора обычно используются призмы из исландского шпата.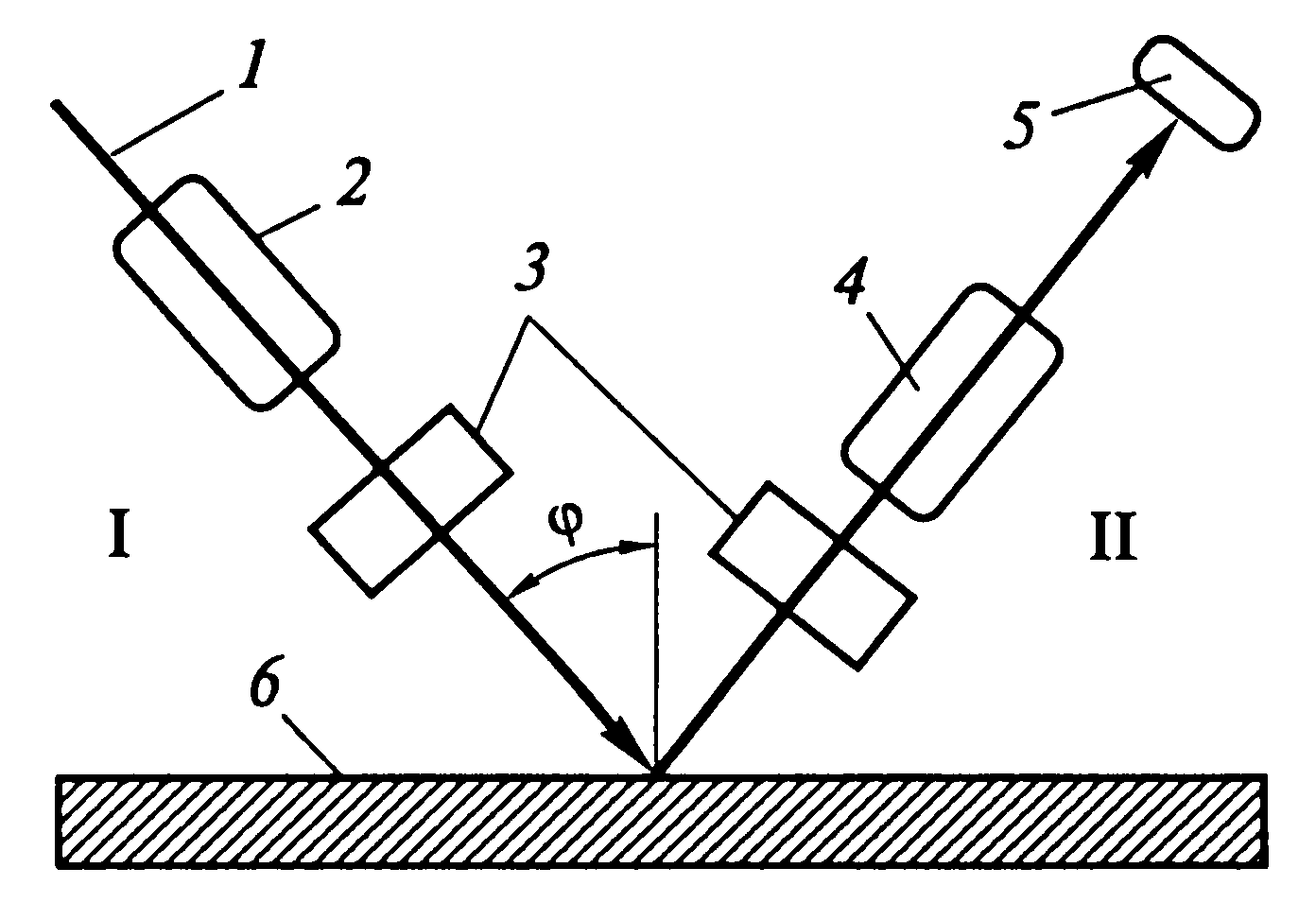



Рис. 7.27. Оптическая схема эллипсометрического метода:

1 — источник света; 2 — поляризатор; 3 — компенсатор (в положении I — схема PKSA; в положении II — схема PSKA); 4 — анализатор; 5 — фотоде­тектор; 6 — отражающая поверхность.

Нулевому отсчету азимута этих элементов соответствует плос­кость с наибольшей степенью поляризации. Компенсатор пред­ставляет собой пластину из двулучепреломляющего кристалла, вырезанную и подобранную по толщине так, чтобы сдвиг фаз между необыкновенными и обыкновенными лучами составлял 90°. Нулевому отсчету азимута компенсатора соответствует плоскость, вдоль которой свет распространяется с наибольшей скоростью — так называемая быстрая ось компенсатора. Для кристаллического компенсатора значения пропусканий вдоль быстрой и медленной осей не совпадают, поэтому реальный компенсатор характеризу­ется, по крайней мере, двумя параметрами: сдвигом фаз и отно­шением пропусканий вдоль быстрой и медленной осей.

Образец устанавливают так, чтобы ось вращения плеч прохо­дила через отражающую поверхность, а плоскость падения была ей перпендикулярна. Угол падения отсчитывается от перпендику­ляра к отражающей поверхности; положительное направление углов поворота поляризационных элементов определяется прави­лом винта; отсчет начинается от плоскости падения.

Компенсатор может располагаться в плече поляризатора (в по­ложении I - схема PKSA) или в плече анализатора (в положении - схема PSKA на рис. 7.28). Эти положения абсолютно эквива­лентны и не влияют на точностные возможности прибора. Прин­цип проведения эллипсометрического измерения в такой схеме заключается в следующем: при схеме PKSA поворотом поляриза­тора добиваются такой эллиптической поляризации на выходе ком­пенсатора (в падающем на образец световом пучке), чтобы после отражения свет стал линейно-поляризованным. В этом случае он может быть погашен путем соответствующего поворота анализа­тора и на выходе эллипсометра (на фотодетекторе) будет наблю­даться нулевая (или минимальная) интенсивность излучения.

При схеме PSKA на отражающую поверхность подается линей­но-поляризованный свет с такой ориентацией плоскости поляри­зации, при которой после отражения свет становится так эллип­тически поляризован, чтобы, пройдя компенсатор, он имел бы линейную поляризацию. Соответственно и в этом случае отражен­ное излучение может быть погашено с помощью поворота анализатора. В связи с этим схема получила название нулевой эллипсо­метрической схемы. Ее главное достоинство заключается в том, что с помощью фотодетектора определяются положения поляри­затора и анализатора, приводящие к минимуму интенсивности света на выходе прибора, а сама по себе величина этой интенсив­ности интереса не представляет. Путем введения модулирующих элементов в оптический тракт эллипсометра осуществляется ав­томатизация эллипсометических измерений.

Наибольшая точность метода обеспечивается при ориентации быстрой оси компенсатора составляет ± 45°. К сожалению, изго­товить идеальный компенсатор не удается. Если повернуть поля­ризатор или анализатор на 180°, то вновь достигается положение гашения. Все возможные положения поляризационных элементов, приводящие к гашению света на выходе эллипсометра, образуют так называемые элипсометрические зоны. Если такие положения разбить по угловым интервалам, в которые попадают азимуты по­ляризационных элементов, то образуется восемь зон, каждая из которых состоит из четырех подзон.

Из этого следует, что если измерены P и A в какой-либо одной подзоне, то состояние поляризации отраженного света может быть однозначно определено только в том случае, если известны пара­метры компенсатора. Однако в процессе работы прибора они су­щественно меняются, причем не монотонно. Это свидетельствует о существовании нескольких причин нестабильности: кроме из­менения температуры в результате прогрева прибора может про­исходить незначительный поворот компенсатора из-за неравно­мерного нагревания плеч эллипсометра. Все это требует тщатель­ной температурной стабилизации компенсатора и всего прибора в целом. Основное уравнение отражательной эллипсометрии име­ет вид: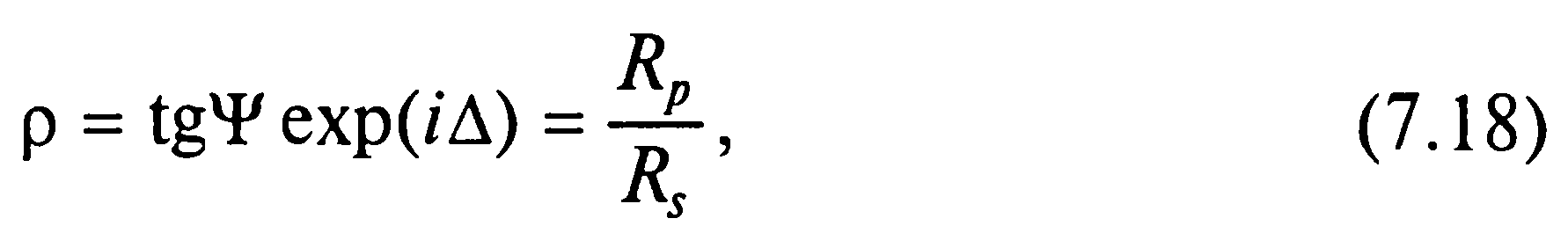


где ρ — относительный коэффициент отражения; Ψ, Δ — эллип­сометрические параметры; R_p, R_s — коэффициенты отражения для p и s компонент электрического вектора (p-компонента лежит в плоскости падения, s-компонента лежит в перпендикулярной ей плоскости).

Уравнение (7.18) определяет физический смысл параметров Δ и Ψ. Коэффициенты отражения R_p и R_s, как правило, являются комплексными величинами. Таким образом, Δ есть разность аргу­ментов этих величин, a tg Ψ — отношение их модулей.

Величины Δ и Ψ (или комплексная величина относительного коэффициента отражения р) не могут служить полной характери­стикой отражательных свойств исследуемой поверхности для не­которого угла падения. Полностью эти свойства описываются ве­личинами Rp и Rs. Выражения для Δ и Ψ применительно к наибо­лее важным видам уже известны и являются функцией структуры отражающей системы — оптических характеристик всех ее эле­ментов и их геометрических размеров. Вычисление значений Δ и Ψ для конкретного вида отражающей системы при всех известных ее параметрах составляет содержание прямой задачи эллипсометрии.

Обратная задача, представляющая интерес, — это определение всех или некоторых параметров отражающей системы по изме­ренным при одном или нескольких углах падения значениям Δ и Ψ. Поскольку эта задача не имеет аналитического решения в общем виде, для ее решения привлекаются различные численные нелинейные методы. Это дает возможность получения аналитиче­ских решений для всех параметров отражающей системы, состоя­щей из однородного изотропного слоя (даже наноразмерного) на изотропной подложке, т.е. определения параметров сверхтонких наноразмерных пленок.