Микроэкономика. Курс лекций. Часть 1. Курс лекций Белгород 2009 удк 330. 101. 8 Ббк 65. 01 Э 59
 Скачать 3.33 Mb. Скачать 3.33 Mb.
|
|
Например, изменение капитала к изменению величины труда будет выглядеть следующим образом: MRTSKL = -K/L. Уменьшая использования одного фактора, например капитала (K), фирма уменьшает объем выпуска на Q = MPK ·(-K). Но для того, чтобы остаться на той же изокванте, сокращение объема используемого капитала должно компенсироваться увеличением применяемого труда (L) на Q = MPL· L. Следовательно, для того чтобы выпуск остался неизменным должно выполняться равенство: MPL · L+ MPK·K=0 или MPL · L= MPK·(-K). Из этого следует, что, MPL / MPK =-K / L = MRTSKL. Таким образом, предельная норма технологического замещения факторов производства равна обратному соотношению их предельных продуктов (производительностей). По мере движения по кривой вниз MRTSKL уменьшается (поэтому кривая имеет выпуклую к началу координат форму). Это объясняется тем, что по мере замещения капитала трудом (сокращение фактора К и увеличения количества фактора L) предельный продукт капитала (МРК) растет, а предельный продукт труда (МРL) уменьшается (числитель убывает, а знаменатель растет). Следовательно, предельная норма технологического замещения капитала трудом убывает. И наоборот. С другой стороны, равенство MPL / MPK =-K / Lговорит о том, что в любой точке изокванты предельная норма замещения одного ресурса другим равна наклону касательной к точке, лежащей на изокванте. MRTSKL - наклон изокванты. Изокванты имеют различный вид в зависимости от степени взаимозаменяемости ресурсов (рис. 8.6). К К К 4 2 1 2 L L L 2 2 2 6 а) Абсолютно б) Комплиментарные в) Частично взаимозаменяемые (взаимодополняемые) взаимозаменяемые Рис. 8.6. Формы изоквант                   Изокванты, имеющими форму прямых линий (рис. 8.6 а), характеризуют идеальную взаимозаменяемость факторов, то есть один фактор может быть полностью заменен другим. В этом случае производство может осуществляться даже при помощи одного фактора. Например, продажа напитков может производиться продавцами, а может автоматами. В этом случае предельная норма технологического замещения постоянна во всех точках изокванты (MRTSKL=cons’t).Тогдапроизводственная функция имеет вид: Q=α∙К+β∙L. Изокванты в виде прямого угла (рис. 8.6 б) отражают закономерности производства с фиксированными пропорциями факторов. В данном случае производственная технология такова, что используемые факторы взаимодополняют друг друга и замещение между ними невозможно (MRTSKL=0). Для того чтобы осуществить процесс производства, оба фактора должны применяться в одной и той же строго определенной пропорции, например, 1 автомобиль и 2 водителя (1 ед. К и 2 ед. L). Обязательным условием перехода на новую изокванту является не только увеличение двух факторов, но и соблюдение заданной пропорции в использовании ресурсов. Если же произойдет увеличение одного фактора без изменения другого, то переход невозможен. Например, сочетание 3 автомобиля и 2 водителей экономически бессмысленно, так же как и сочетание 1 автомобиль 6 водителей. Переход на более высокую изокванту в данном случае возможен при сочетании 3 автомобиля и 6 водителей. В этом случае взаимодополняемых факторов производственная функция имеет вид (формула «затраты-выпуск» или формула В.В. Леонтьева): Q=f(K,L) = min{αК,βL}. Это означает, что объем выпуска будет равен минимальной из величин, которые будут получены при подстановке в функцию количественных значений переменных факторов. Допустим α=3, β= 2, К=1, L=2, то объем выпуска будет равен 3, так как Q= min{3(1),2(2)}. Тогда объем будет равен 3 и 4. В случае частично взаимозаменяемых факторов (рис. 8.6 в) производство продукции может осуществляться с обязательным использованием двух факторов. Их комбинации могут быть различными в зависимости от заданной производственной функции (формула Кобба-Дугласа): Q=А∙Кα∙Lβ. Фирма, осуществляющая свою деятельность с использованием двух переменных факторов, сталкивается с проблемой оптимального выбора комбинации ресурсов при каждом заданном объеме выпуска. Фирма, максимизирующая прибыль, будет стремиться выбрать такое сочетание ресурсов, которое окажется самым дешевым. Таким образом, задача сводится к тому, чтобы минимизировать издержки фирмы для каждого заданного объема производства. Подобно тому, как один и тот же объем выпуска может быть получен при различных комбинациях факторов, разные их сочетания могут дать одинаковый уровень издержек. Линия, отражающая разные комбинации факторов производства, дающих равные суммарные издержки, называется изокостой (рис. 8.7). Изобразим графически общие издержки: ТС = РК∙К+РL∙L, где ТС – общие издержки, равные сумме постоянных и переменных; РК – цена единицы капитала; К- количество капитала; РL- цена единицы труда; L– количество труда. 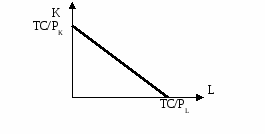 4 Рис. 8.7. Изокоста Изокоста строится следующим образом. Если предположим, что все тратится только на приобретение капитала, то можно приобрести максимально ТС/РК ед. Если все тратится только на приобретение труда, то можем приобрести максимально ТС/РL ед. Соединив эти пограничные точки, получим изокосту (рис. 8.7). Любая точка на изокосте показывает такое сочетание двух факторов, при котором совокупные расходы (общие издержки) на их приобретение равны. Изокоста описывается уравнением: ТС= РК∙К+РL∙L, Угол наклона изокосты равен предельной норме технологического замещения: Таким образом, наклон изокосты равен отношению цен используемых факторов, умноженных на (-1). Если фирма увеличит количество одного фактора, то она должна сократить использование другого. Для того чтобы сохранить неизменными совокупные расходы на приобретение факторов должно выполняться следующее условие: -K / L = PL / PK. Поскольку, изокоста – это одновременно и линия равных издержек, и линия бюджетного ограничения фирмы, тогда уравнение может иметь вид: В= РК∙К+РL∙L, где В – бюджет фирмы, предназначенный для закупки факторов; РК – цена единицы капитала; К – количество капитала; РL– цена единицы труда; L – количество труда. Например, бюджет фирмы, предназначенный для закупки факторов, 1000 руб., а цена 1 единицы капитала 500 руб., а единицы труда 250 руб. В этом случае фирма может приобрести 2 единицы капитала или 4 единицы труда (рис. 8.8). Изменение величины бюджета вызывает сдвиг изокосты влево (уменьшился) или вправо (увеличился) (рис. 8.9 а). Изменение цены на факторы производства приводит к изменению угла наклона изокосты (рис. 8.9 б). Но возможны случаи одновременного изменения и бюджета, и цен на факторы производства. 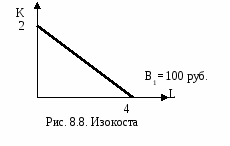 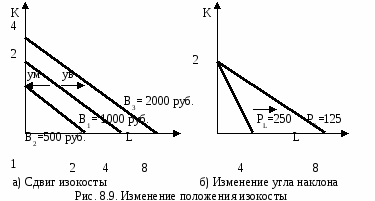 Задача предпринимателя состоит в том, чтобы выбрать такую комбинацию факторов, которая обеспечивает производство необходимого количества продукции с наименьшими издержками. Оптимальным будет такое соотношение факторов, когда комбинация данных ресурсов лежит на изокосте, а наклон изокосты равен наклону изокванты, т.е. Это равенство говорит о том, что минимальные издержки достигаются тогда, когда затраты на дополнительную единицу продукции не изменяются от использования любых дополнительных факторов. Для определения оптимального сочетания наложим карту изоквант на изокосту (рис. 8.10). Изокоста с бюджетными ограничениями В1 (или издержками С1) не позволяет достичь требуемого выпуска, поскольку не имеет точки касания с изоквантой. Пересечение изокосты с изоквантами мы видим в точках А, В и D. Точки В и D указывают на чрезмерно высокие затраты (В3) для достижения данного объема выпуска Q. Точка А является оптимальной, поскольку именно эта комбинация факторов позволяет произвести объема Q при меньших затратах (В2). 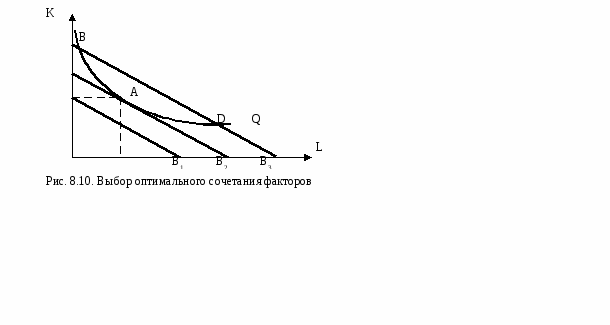 Фирма в целях увеличения или сокращения объемов производства должна изменять соотношение факторов до тех пор, пока предельна норма замещения факторов (MRTSKL) не будет равна наклону изокосты (PL/PK). Отсюда следуют следующие выводы: 1) фактор производства применяется до тех пор, пока его предельная производительность, выраженная в денежных единицах, не станет равной его рыночной цене, являющейся ограничительным пределом применения фактора; 2) оптимальная комбинация фактора достигается тогда, когда соотношение предельных производительностей факторов равно соотношению их рыночных цен; 3) соотношение цен и предельных производительностей факторов производства обусловливает спрос в отношении каждого из них. В краткосрочном периоде если цена на какой-либо фактор растет, то фирма будет сокращать его использование и увеличивать более дешевый. Однако изменение использования факторов производства приводит к изменению издержек производства. И любое ограничение по использованию какого-либо фактора приведет к росту издержек и не позволит фирме добиться оптимального сочетания факторов. Однако в долгосрочном периоде фирма располагает боле широкими возможности для комбинирования факторов для каждого заданного объема производства, поскольку издержки в долгосрочном периоде ниже издержек в краткосрочном. Определив оптимальное соотношение факторов для объема Q, можно проделать это же для объемов Q1, Q2 и т.д. В результате получим некую карту оптимальных с точки зрения издержек вариантов осуществления производства (рис. 8.11). Комбинация факторов в точке А даст наименьшие издержки при объеме Q1, в точке В при объеме Q2, в точке С при объеме Q3. Соединив все точки оптимумов для различных объемов производства (А, В, С) получим кривую, называемую траекторией роста.
Принимая решения об изменении объемов производства, фирма будет двигаться вдоль данной кривой.  Направление траектории зависит от соотношения цен факторов и их предельных производительностей. Для большинства производителей наиболее вероятным является смещение в сторону капитала из-за перехода к более капиталоемким технологиям (рис. 8.12 а). Если технология требует постоянного соотношения факторов, то будет наблюдаться линейная траектория развития (рис. 8.12 б). Если в редких случаях требуется применение большого количества труда, то имеет место понижающая траектория развития (рис. 8.12 в). Как было сказано выше, в точке касания наклоны изокванты и изокосты равны. Наклон изокосты равен PL/PK, а изокванты – MRTSKL.. MRTSKL = MPL / MPK = -K / L, но -K/L= PL / PK. Тогда MPL/ MPK= PL/PK, то есть:
К К К L L L а) Капиталоемкие б) Смешанные в) Трудоемкие Рис. 8.12. Различные формы траектории развития технологий         
|
