В.К.Багазеев Основы горной геомеханики. Курс лекций Екатеринбург, 2021 удк 622. 831 Рецензенты Зотеев О. В. Вандышев А. М
 Скачать 4.36 Mb. Скачать 4.36 Mb.
|
|
8.4. Определение напряжений на наклонных площадках при одноосной нагрузке ЗАДАНИЕ 4. Рассчитать напряжение 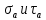 на наклонной площадке под углом на наклонной площадке под углом 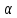 при одноосной силе P. Построить круг Мора. при одноосной силе P. Построить круг Мора.
РЕШЕНИЕ. Под действием внешних сил в массиве пород возникают внутренние силы, препятствующие деформации и разрушению массива (рис. 8.3).   а б 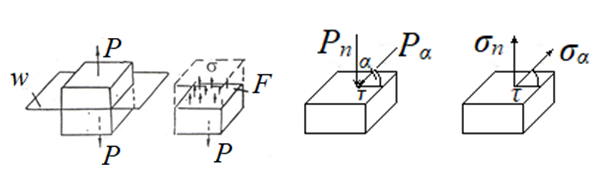 Рис. 8.3. Схема действия внутренних сил – напряжений: при нормальной (а) и наклонной (б) к площадке силе Величина внутренних сил, приходящаяся на единицу площади, называется напряжением, обозначается 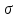 (сигма), единица измерения Па (Н/м2): (сигма), единица измерения Па (Н/м2): 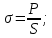 где 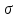 – напряжения на площадке S$ – напряжения на площадке S$ 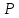 – внешняя сила; – внешняя сила; 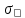 – напряжения от наклонной нагрузки; – напряжения от наклонной нагрузки; 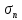 – нормальная составляющая напряжений; – нормальная составляющая напряжений; 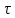 – касательная составляющая напряжений; – касательная составляющая напряжений; 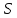 – площадь, на которую действуют внутренние силы. – площадь, на которую действуют внутренние силы. 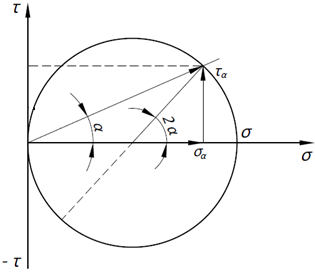  Рис. 8.4. Графическое изображение напряжений на наклонных площадках Напряжения на наклонных под углом 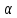 сечениях при одноосной нагрузке сечениях при одноосной нагрузке 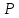 определяется по формулам: определяется по формулам: 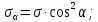 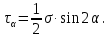 где 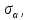 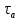 – нормальные и касательные напряжения. Графически эти напряжения выражаются кругом Мора (рис. 8.4). – нормальные и касательные напряжения. Графически эти напряжения выражаются кругом Мора (рис. 8.4). 8.5. Оценка начального напряженного состояния пород в упругом массиве ЗАДАНИЕ 5. Определить компоненты начального поля напряжений 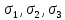 в точке М на глубине H (м) в породах с объемным весом в точке М на глубине H (м) в породах с объемным весом 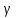 ( (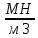 ) и коэффициентом Пуассона ) и коэффициентом Пуассона 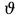 в ортогональной сетке координат. в ортогональной сетке координат.
РЕШЕНИЕ. Породы массива находятся в естественном напряженном состоянии. На глубине Н (м) действуют нормальные напряжения сжатия, обусловленные весом вышележащих пород: 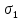 – вертикально направленные, – вертикально направленные, 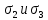 – направлены горизонтально (рис. 8.5). – направлены горизонтально (рис. 8.5). 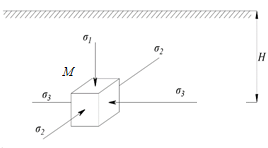 Рис. 8.5. Компоненты начального поля напряжений на гранях элементарного кубика в ортогональной сетке координат ( Рис. 8.5. Компоненты начального поля напряжений на гранях элементарного кубика в ортогональной сетке координат (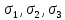 – главные напряжения) – главные напряжения)Если принять массив как сплошную упругую среду, то величина напряжений рассчитывается по формулам: 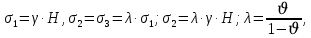 где 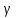 – объемный вес вмещающих пород; – объемный вес вмещающих пород; 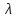 – коэффициент горизонтального распора; – коэффициент горизонтального распора; 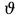 – коэффициент Пуассона. – коэффициент Пуассона. Величина 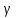 , , 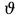 зависит от типа пород и принимается по справочным данным. Например, средний объемный вес алевролитов и аргиллитов зависит от типа пород и принимается по справочным данным. Например, средний объемный вес алевролитов и аргиллитов 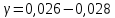 МН/м3, а коэффициент Пуассона МН/м3, а коэффициент Пуассона 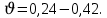 8.6. Определение напряжений на наклонных площадках при объемной нагрузке ЗАДАНИЕ 6. Рассчитать величину главных напряжений 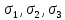 и угол между осью координат х и направлением и угол между осью координат х и направлением 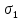 . .
РЕШЕНИЕ. Поверхность горных выработок, как правило, находится под углом к направлению 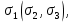 т. е. на наклонных площадках, на которых возникают касательные напряжения т. е. на наклонных площадках, на которых возникают касательные напряжения 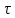 . В общем случае на каждой грани элементарного кубика будет действовать три напряжения: одно нормальное . В общем случае на каждой грани элементарного кубика будет действовать три напряжения: одно нормальное 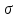 и два касательных и два касательных 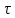 (рис. 8.6). (рис. 8.6). 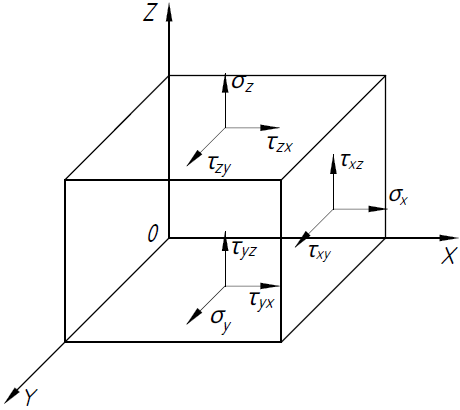 В табличной форме в виде матрицы эти напряжения составляют тензор напряжений В табличной форме в виде матрицы эти напряжения составляют тензор напряжений 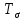 : : 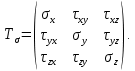  Рис. 8.6. Компоненты напряжений при объемном напряженном состоянии В любой точке массива всегда можно провести три взаимно перпендикулярные площадки, в которых отсутствуют касательные напряжения, а действуют только нормальные напряжения 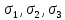 (рис. 8.7). (рис. 8.7). 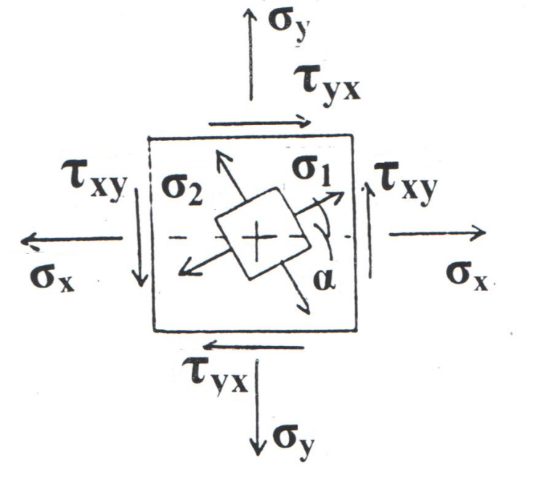 Таким образом, количество независимых компонентов, характеризующих напряженное состояние уменьшается до трех, тогда  Рис. 8.7. Ориентация сетки координат 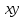 относительно главных напряжений относительно главных напряжений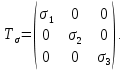 Площадки, на которых отсутствуют касательные напряжения, называются главными. Нормальные напряжения на этих площадках такие называются главными напряжениями 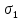 > > 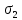 > > 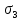 . . В условиях плосконапряженного или плоскодеформированного состояния ( 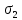 = = 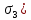 упрощается переход от значений компонент напряжений в декартовых упрощается переход от значений компонент напряжений в декартовых 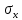 , , 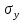 осях к главным напряжениям: осях к главным напряжениям: 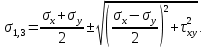 Угол α между осью X и направлением действия максимального сжимающего напряжения 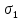 можно определить следующим образом: можно определить следующим образом: 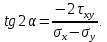 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

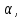 град
град