В.К.Багазеев Основы горной геомеханики. Курс лекций Екатеринбург, 2021 удк 622. 831 Рецензенты Зотеев О. В. Вандышев А. М
 Скачать 4.36 Mb. Скачать 4.36 Mb.
|
|
4.2. Представление напряжений в полярной системе координат В предыдущих лекциях мы представляли графически напряжения в прямоугольной (Декартовой) системе координат. Положение точки на плоскости определяется двумя координатами 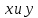 , в трехмерном пространстве тремя координатами , в трехмерном пространстве тремя координатами 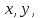 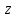 . Во многих случаях, когда тело ограничено поверхностями кругового цилиндра и родиально нисходящимися плоскостями, плоскую задачу удобно рассматривать в полярной системе координат, в которой координаты точки определяются величиной полярного радиуса r и полярного угла θ (рис. 4.3). . Во многих случаях, когда тело ограничено поверхностями кругового цилиндра и родиально нисходящимися плоскостями, плоскую задачу удобно рассматривать в полярной системе координат, в которой координаты точки определяются величиной полярного радиуса r и полярного угла θ (рис. 4.3).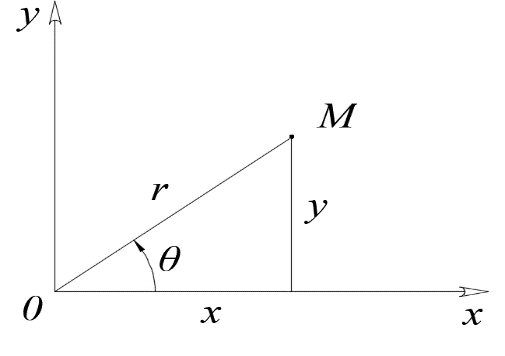  Рис.4.3. Координаты точки М в прямоугольной системе координат x, y и в полярной системе r и θ Совместив полюс полярной системы координат (r, θ) с началом декартовой системы координат ( 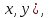 а полярную ось абцисс – с осью абцисс (рис.4.3), нетрудно установить связь между координатами произвольной точки M в этих двух системах координат: а полярную ось абцисс – с осью абцисс (рис.4.3), нетрудно установить связь между координатами произвольной точки M в этих двух системах координат: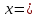 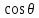 ; ; 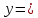 г г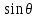 . .Обратные зависимости имеют вид 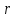 = =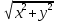 ; ; 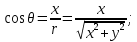 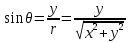 . .Связь между напряжениями в декартовых и полярных координатах проследим на графиках (рис. 4.4): 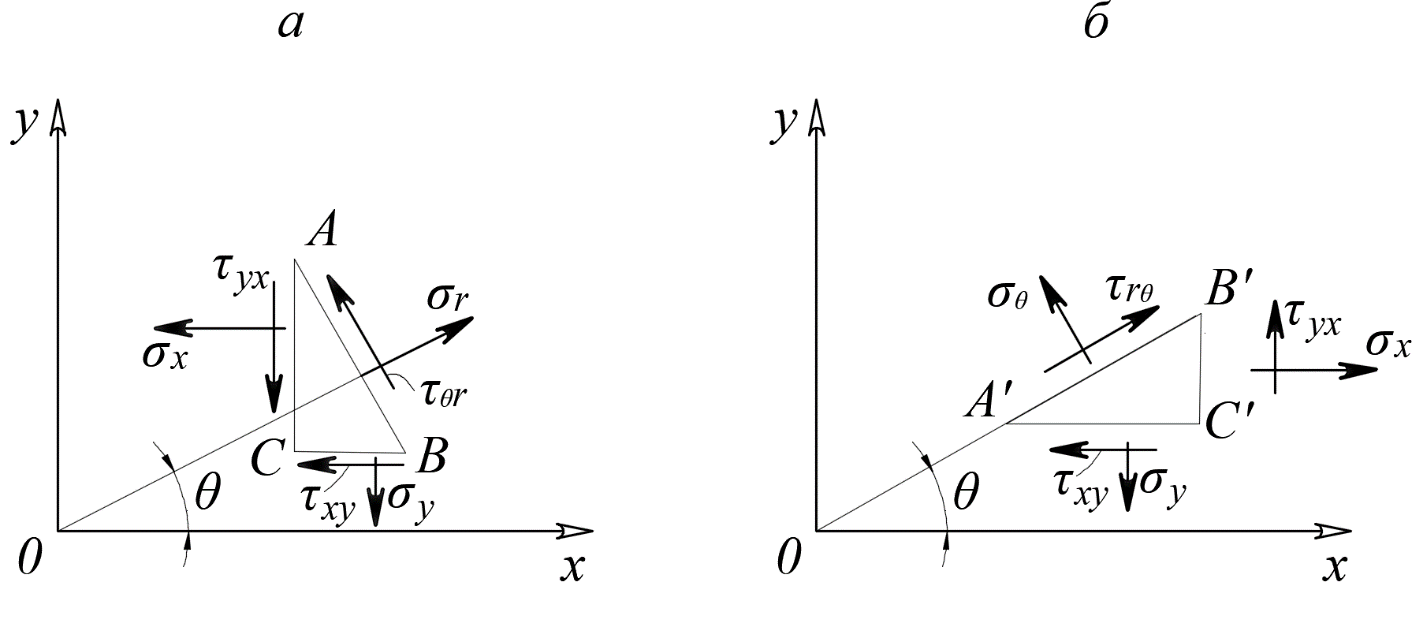 Рис. 4.4. Напряжения на гранях призмы АВ: а – перпендикулярно полярному радиусу б – параллельно полярному радиусу. 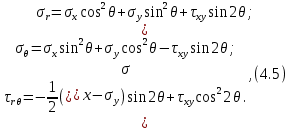 после преображений 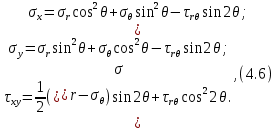 Сложив почленно первые две из формул 4.5 или 4.6, получим подтверждение известного свойства первого инварианта тензора напряжений при двухосном напряженном состоянии: 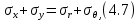 где 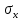 , , 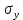 – нормальные напряжения в прямоугольных координатах; – нормальные напряжения в прямоугольных координатах; 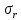 – нормальные родиальные; – нормальные родиальные; 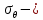 нормальные тангенциальные напряжения в полярных координатах; нормальные тангенциальные напряжения в полярных координатах; 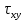 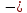 касательные напряжения в прямоугольных координатах; касательные напряжения в прямоугольных координатах; 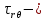 касательные напряжения в полярных координатах. касательные напряжения в полярных координатах.4.3. Расчет напряжений вокруг круглого ствола шахты Рассмотрим напряжения в поперечном сечении незакрепленного шахтного ствола круглой формы. Решение подобной задачи проведено в курсе сопротивления материалов в полярной системе координат (рис. 4.5) 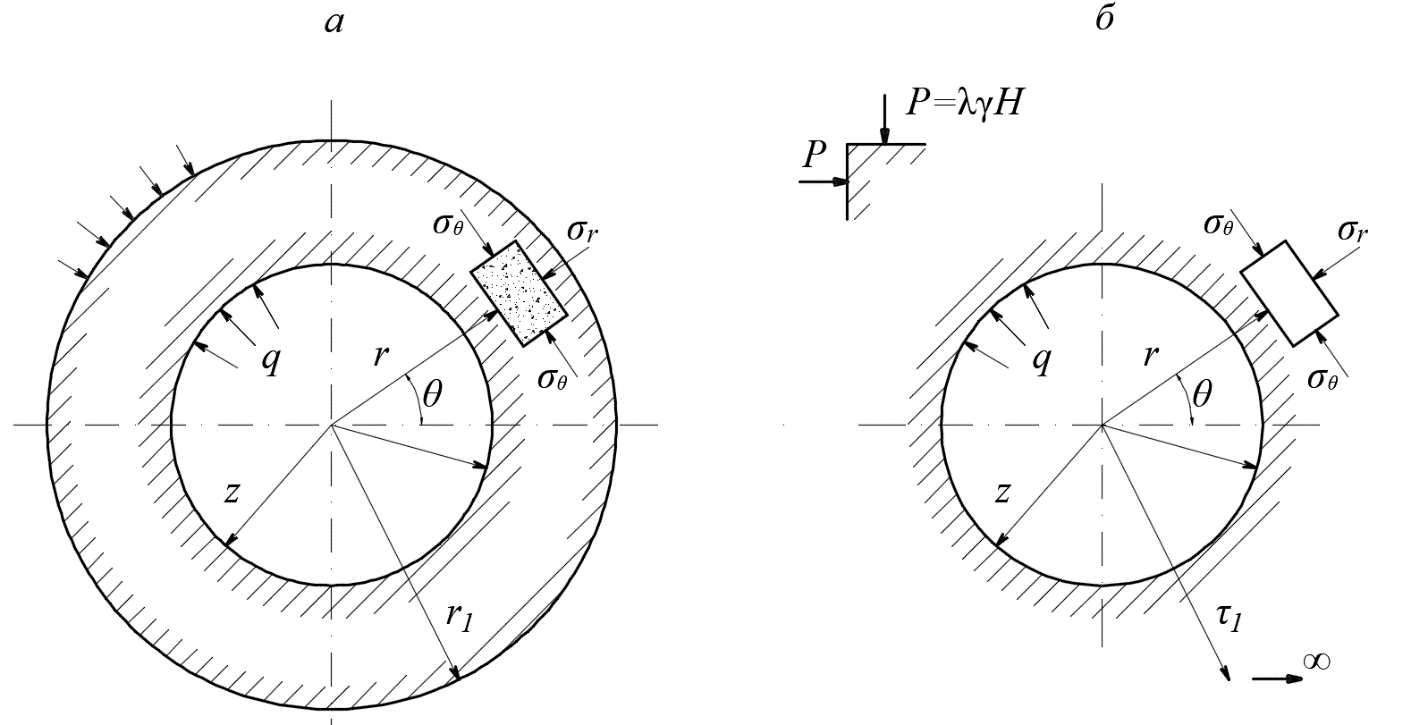 Рис. 4.5. Напряженное состояние: а – кольца́; б – вокруг ствола шахты Получено уравнение (рис. 4.5. а) 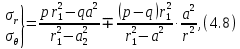 Чтобы получить напряжения вокруг ствола (рис.4.5. б), в формуле (4.5) необходимо устремить внешний радиус кольца 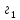 к бесконечности, к бесконечности,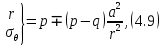 где 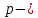 исходное напряженное состояние массива, можно для вертикального ствола принять исходное напряженное состояние массива, можно для вертикального ствола принять 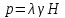 , Па; , Па;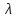  коэффициент бокового распора (0 коэффициент бокового распора (0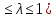 ; ;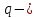 отпор крепи, Па; отпор крепи, Па;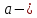 радиус выработки, м; радиус выработки, м;где Р 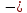 исходное напряженное состояние массива, для вертикального ствола шахты Р= исходное напряженное состояние массива, для вертикального ствола шахты Р=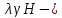 коэффициент бокового распора, коэффициент бокового распора, 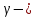 удельный вес пород, удельный вес пород, 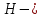 глубина рассматриваемого сечения ствола, глубина рассматриваемого сечения ствола, 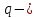 отпор крепи, отпор крепи, 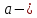 радиус выработки, радиус выработки, 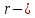 текущий радиус (расстояние от центра ствола до рассматриваемой точки), м. Для незакрепленного ствола: текущий радиус (расстояние от центра ствола до рассматриваемой точки), м. Для незакрепленного ствола: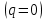 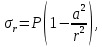 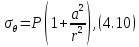 Проанализируем важные закономерности распределения вокруг незакрепленного ствола (рис. 4.6): 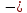 напряжения не зависят от упругих постоянных; напряжения не зависят от упругих постоянных;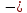 на контуре на контуре 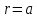 , концентрация , концентрация 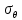 максимальна максимальна 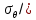 Р=2, т.е. Р=2, т.е. 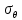 удваивается и не зависит от размеров ствола; удваивается и не зависит от размеров ствола;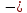 напряжение напряжение 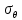 и и 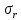 по мере роста по мере роста 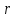 быстро стремятся к быстро стремятся к 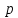 ; ;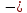 максимальное касательное напряжение максимальное касательное напряжение 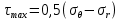 , вызывающее разрушение пород, быстро снижается до нуля и на расстоянии , вызывающее разрушение пород, быстро снижается до нуля и на расстоянии 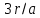 равно только 11 % от его значения на контуре. равно только 11 % от его значения на контуре.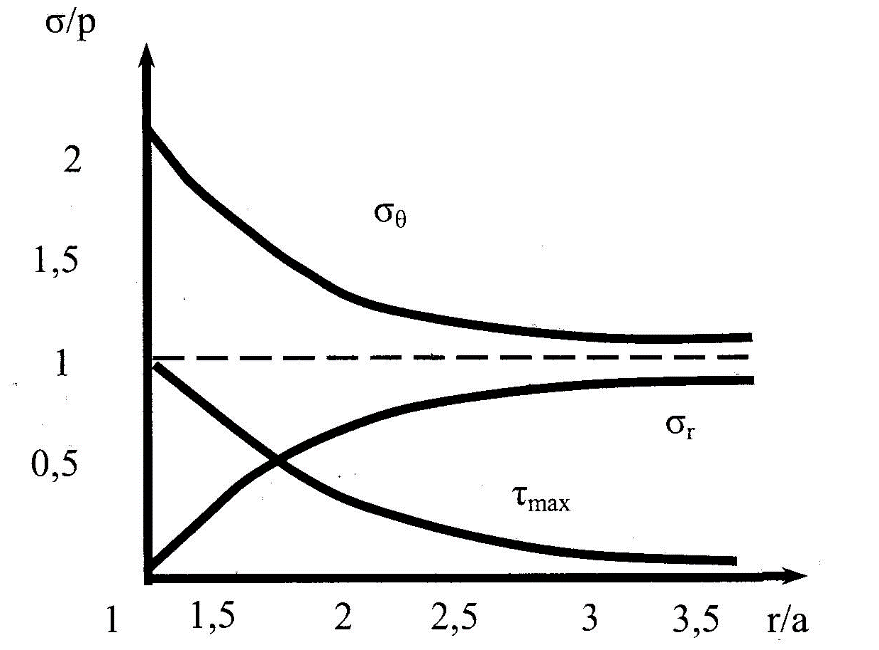  Рис. 4.6. График изменения напряжений вокруг ствола Напряжения вокруг сферической выработки в гидростатически нагруженном массиве 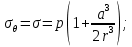 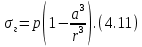 Эти формулы пригодны для приближенной оценки напряжений вокруг камер, сопряжений, забоев выработок. Лекция 8 4.4. Распределение напряжений вокруг горизонтальной выработки круглого сечения Решения о распределении напряжений вокруг горизонтальной круглой выработки получены также как и для ствола в полярной системе координат 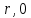 . При одноосной нагрузке . При одноосной нагрузке 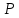 в массиве пород (под которой понимаем первоначальное вертикальное нормальное напряжение) вокруг выработки действуют нормальные тангенциальные в массиве пород (под которой понимаем первоначальное вертикальное нормальное напряжение) вокруг выработки действуют нормальные тангенциальные 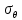 («окружные»), радиальные («окружные»), радиальные 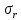 (по радиусу (по радиусу 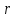 )напряжения и касательные напряжения )напряжения и касательные напряжения 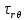 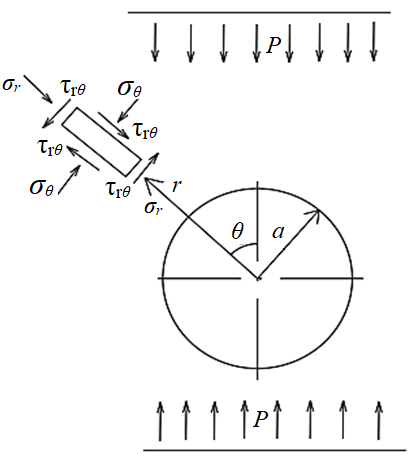 Рис. 4.7. Схема к расчету напряжений вокруг выработки круглого сечения при действии равномерно распределенной нагрузки Р: а – радиус выработки; Рис. 4.7. Схема к расчету напряжений вокруг выработки круглого сечения при действии равномерно распределенной нагрузки Р: а – радиус выработки; r– радиус-вектор до рассматриваемой точки; θ – угол между радиус -вектором и направлением действия нагрузки. Величина напряжений в обозначениях рис. 4.7. рассчитывается по формулам: 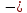 нормальные радиальные нормальные радиальные 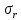 и тангенциальные и тангенциальные 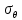  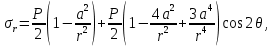 (4.12) (4.12)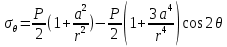 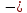 касательные касательные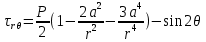 Коэффициент концентрации тангенциальных нормальных напряжений на контуре при 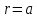 и одноосной нагрузке и одноосной нагрузке 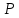 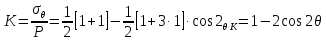 (4.13) (4.13) 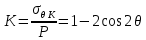 Например: в стенках выработки при одноосной нагрузке 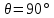 , ,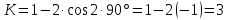 В приконтурной верхней части выработки радиальные напряжения меняют знак (на растяжение), коэффициент концентрации при 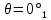 достигает достигает 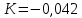 . .Поскольку один из размеров подготовительных и капитальных выработок (обычно длина) во много раз превышает два других, объемная задача по вычислению напряжений и перемещений вокруг горизонтальной выработки сводится к плоской, т. е. к рассмотрению напряжений и перемещений вокруг поперечного сечения выработки. 4.5. Распределение напряжений вокруг горизонтальной горной выработки в упругой среде при двухосной нагрузке Под действием двух ортогональных нагрузок 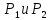 компоненты напряжений определяются по формулам: компоненты напряжений определяются по формулам: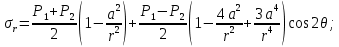 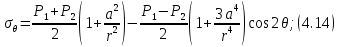 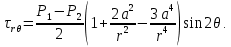 С учетом, что при гравитационном напряженном состоянии 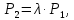 при при 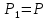 ; ; 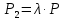 ; ; 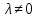 (рис. 4.8). Формулы можно записать в следующем виде: (рис. 4.8). Формулы можно записать в следующем виде: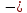 нормальные напряжения нормальные напряжения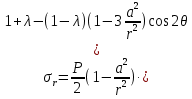 (4.15) 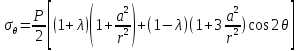 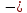 касательные напряжения касательные напряжения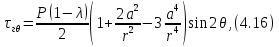 Большое значение имеют напряжения на контуре выработки, т. е. при 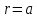 : :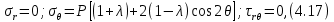 Соответствующий коэффициент концентрации напряжений 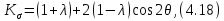 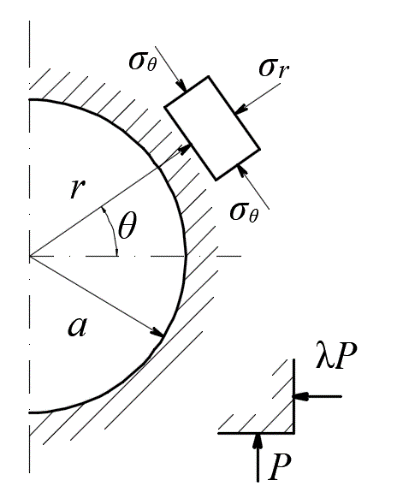 Рис. 4.8. Напряжения вокруг круговой горизонтальной выработки: а – радиус выработки, r – текущий радиус от центра под углом θ к горизонту, σr – нормальные радиальные напряжения, σθ – нормальные тангенциальные напряжения, Р – вертикальная нагрузка, λР – горизонтальное давление 4.6. Эпюры напряжений вокруг технологических выработок Концентрация напряжений в массиве вокруг выработок зависит от глубины их размещения, от величины вертикальных 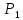 и горизонтальных и горизонтальных 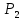 нагрузок, их соотношения нагрузок, их соотношения 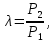 формы и размеров выработок на рис. 4.9-4.11 приводятся эпюры напряжений вертикальных формы и размеров выработок на рис. 4.9-4.11 приводятся эпюры напряжений вертикальных 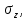 горизонтальных горизонтальных 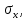 их суммы их суммы 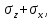 нормальных тангенциальных нормальных тангенциальных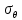 напряжений. напряжений.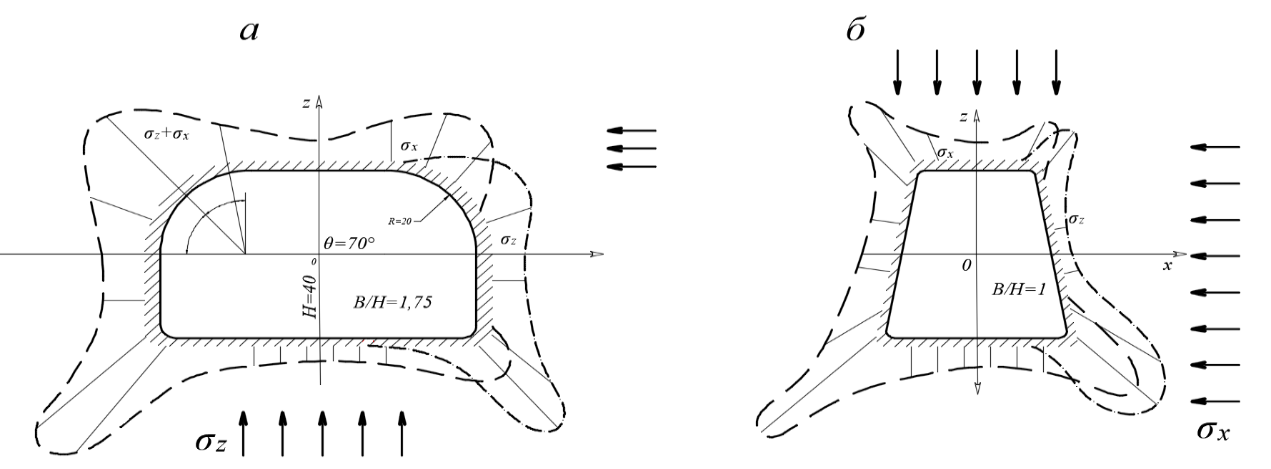 Рис. 4.9. Эпюры вертикальных σz, горизонтальных σx, и сумма σz + σxнапряжений на контуре сводчатой и трапециевидной формы поперечного сечения При гидростатическом напряженном состоянии, когда давление Р одинаково λ=1, на контуре выработки сжимающее напряжение σθ = 2Р, коэффициент концентрации напряжений Кσ=2 (рис.4.10). 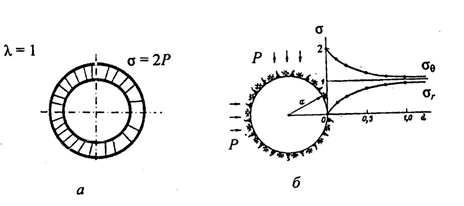 Рис. 4.10. Распределение напряжений на контуре выработки при λ=1: а – эпюра, б – график, d – диаметр выработки При гравитационном напряженном состоянии (при 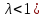 напряжение в кровле и боках выработки существенно различны. В районе кровли напряжение в кровле и боках выработки существенно различны. В районе кровли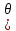 около 90 %) появляется область напряжений обратного знака около 90 %) появляется область напряжений обратного знака 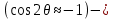 область растягивающих напряжений. Сжимающие напряжения принимают большие значения в боках выработки (рис. 4.11). область растягивающих напряжений. Сжимающие напряжения принимают большие значения в боках выработки (рис. 4.11).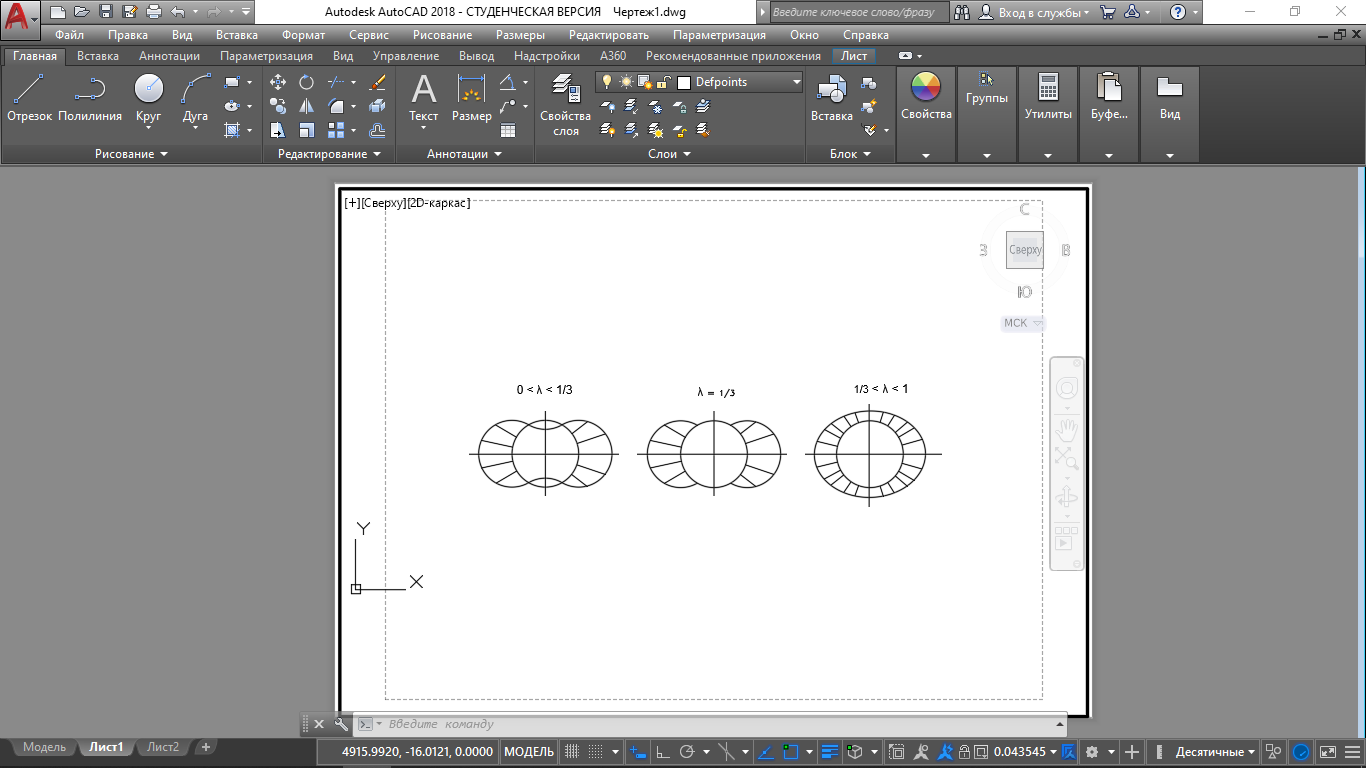 Рис. 4.11. Распределение напряжений на контуре круглой выработки при 0˂λ˂1 П 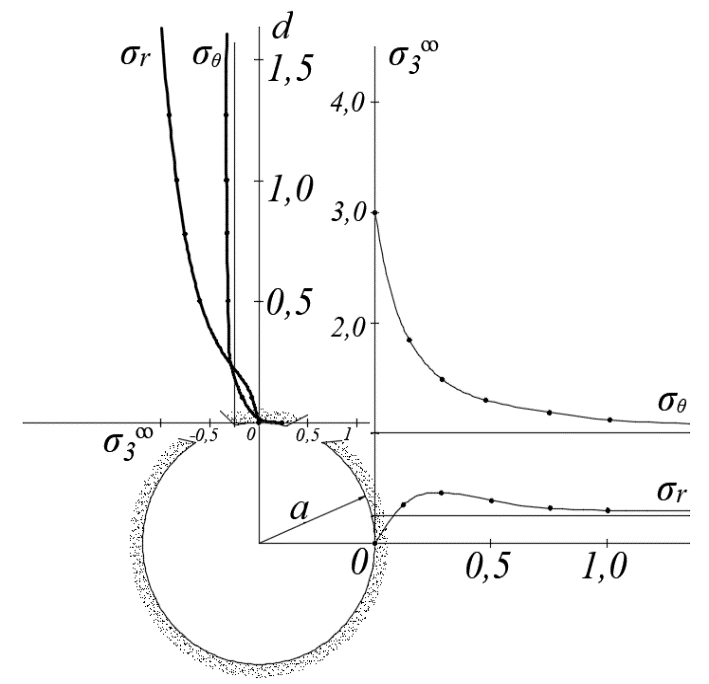 ри естественном поле напряжений ри естественном поле напряжений 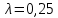 (коэффициент Пуассона (коэффициент Пуассона 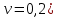 максимальный коэффициент концентрации напряжений максимальный коэффициент концентрации напряжений 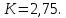  Рис. 4.12. Распределение напряжений вокруг круглой выработки в естественном поле напряжений (λ=0,25) При действии гравитационно-тектонических сил при 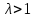 максимальные концентрации напряжений наблюдаются в кровле горизонтальных выработок, а коэффициенты концентрации напряжений составляют максимальные концентрации напряжений наблюдаются в кровле горизонтальных выработок, а коэффициенты концентрации напряжений составляют 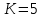 при при 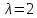 и и 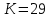 при при 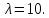 На расстоянии 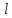 от контура величина напряжений вокруг выработки снижается и до величины естественного напряжения. Это расстояние называется радиусом влияния выработки. от контура величина напряжений вокруг выработки снижается и до величины естественного напряжения. Это расстояние называется радиусом влияния выработки.Вычисления по формулам показывают, что для условий гидростатического напряженного состояния нетронутого массива уже на расстоянии (где d = 2α) значения и тангенциальных и радиальных составляющих отличаются от соответствующих компонент напряжений в нетронутом массиве не более чем на 5 %. Для других условий нагружения наблюдаются существенные различия в скорости затухания напряжений 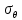 и и 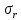 по мере удаления от контура выработки. При этом, как правило, быстрее затухают те компоненты, которые имеют большие коэффициенты концентраций на контуре. по мере удаления от контура выработки. При этом, как правило, быстрее затухают те компоненты, которые имеют большие коэффициенты концентраций на контуре.Так, при 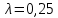 наиболее быстро затухает тангенциальное напряжение наиболее быстро затухает тангенциальное напряжение 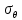 в стенке выработки, уже на расстоянии в стенке выработки, уже на расстоянии 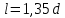 от контура оно отличается на 5 % от значения такового в нетронутом массиве. Остальные компоненты (в том числе и в кровле) затухают медленнее и указанного уровня достигают лишь на расстоянии от контура оно отличается на 5 % от значения такового в нетронутом массиве. Остальные компоненты (в том числе и в кровле) затухают медленнее и указанного уровня достигают лишь на расстоянии 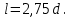 |
