В.К.Багазеев Основы горной геомеханики. Курс лекций Екатеринбург, 2021 удк 622. 831 Рецензенты Зотеев О. В. Вандышев А. М
 Скачать 4.36 Mb. Скачать 4.36 Mb.
|
|
3.4. Природное напряженное состояние массива пород 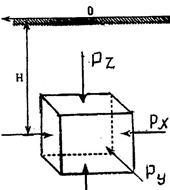 В общем случае в массиве пород на элементарную точку или элементарный объем действуют следующие силы: В общем случае в массиве пород на элементарную точку или элементарный объем действуют следующие силы: 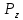 – вертикальная сила вышележащих пород и равная ей вертикальная сила снизу – сила отпора нижележащих пород. Аналогично действуют силы в направлении осей координат – силы бокового отпора пород. Элементарный объем находится в равновесии, т. к. силы, действующие на него, равны между собой. – вертикальная сила вышележащих пород и равная ей вертикальная сила снизу – сила отпора нижележащих пород. Аналогично действуют силы в направлении осей координат – силы бокового отпора пород. Элементарный объем находится в равновесии, т. к. силы, действующие на него, равны между собой. Рис. 2.9. Схема действия сил в массиве пород: Pz – в направлении оси координат z; Px – в направлении оси x; Py – в направлении оси y До начала горных работ на месторождении массив уже находится в напряженном состоянии. Это исходное состояние называется природным напряженным состоянием массива горных пород. Как уже указывалось при трехосной нагрузке в массиве возникает объемное напряженное состояние, характеризуемое тензором напряжений 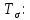 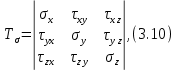 где 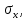 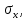 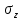 – нормальные напряжения ориентированные по осям координат; – нормальные напряжения ориентированные по осям координат; 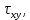 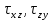 – касательные напряжения. – касательные напряжения.Площадки, на которых действуют только нормальные напряжения, а касательные напряжения отсутствуют, называются главными площадками. Нормальные напряжения, действующие на главных площадках, называются главными. Главные нормальные напряжения по их величинам обозначают следующим образом: 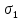 – максимальные; – максимальные; 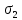 –промежуточные; –промежуточные; 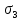 – минимальные. – минимальные.Источником природных напряжений в массиве являются два независимых фактора: силы собственного веса пород и тектонические процессы в земной коре. Поэтому в земной коре, как правило, одно из главных напряжений является вертикальным. Данное направление задается действием силы гравитации. Следовательно, второе и третье главные напряжения должны быть горизонтальными, действующими в двух взаимно перпендикулярных направлениях в плане. Вопросы только в том, каковы величины этих напряжений и как они ориентированы в пространстве. На глубине H в массиве горных пород с удельным весом 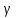 возникают вертикальные напряжения. возникают вертикальные напряжения.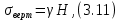 Фактически это давление собственного веса пород от поверхности до глубины H. На земной поверхности (т.е. при 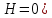 вертикальные напряжения равны нулю. С увеличением глубины растут и вертикальные напряжения. вертикальные напряжения равны нулю. С увеличением глубины растут и вертикальные напряжения. По результатам определения вертикальных напряжений во многих точках земного шара установлено 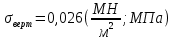 . Это означает, что средний удельный вес пород земной коры можно принять . Это означает, что средний удельный вес пород земной коры можно принять 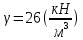 . .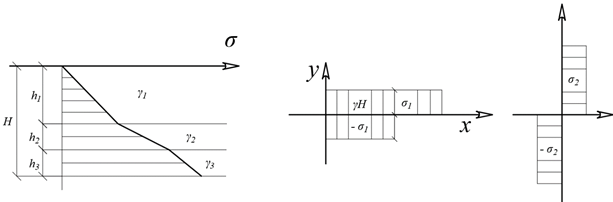 На рис. 2.10. приводятся эпюры напряжения массива пород в естественном состоянии. На рис. 2.10. приводятся эпюры напряжения массива пород в естественном состоянии.Рис. 2.10. Эпюры напряжений: а – распределение по глубине; б – распределение на горизонте Н; σ1, σ2 сжимающие; ( -σ1, - σ2) – растягивающие напряжения. Вертикальное сжатие массива собственным весом вышележащих пород должно вызывать поперечные деформации пород с коэффициентом Пуассона 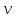 . Однако в сплошном массиве поперечные деформации невозможны. В упругом массиве, нагруженном вертикальном давлении . Однако в сплошном массиве поперечные деформации невозможны. В упругом массиве, нагруженном вертикальном давлении 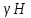 , поперечные деформации пород создаются горизонтальными напряжениями , поперечные деформации пород создаются горизонтальными напряжениями 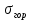 бокового распора: бокового распора: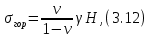 Впервые приведенную выше формулу для упругой модели массива, нагруженной только одной активной силой –собственным весом, получил в 1925 г. советский ученый, академик А. Н. Динник. Коэффициент 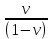 называют коэффициентом бокового распора по А. Н. Диннику. Его величина зависит только от коэффициента Пуассона называют коэффициентом бокового распора по А. Н. Диннику. Его величина зависит только от коэффициента Пуассона 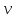 упругих пород. упругих пород.Для большинства горных пород коэффициент Пуассона можно принять равным 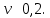 Тогда коэффициент бокового распора (соотношение горизонтальных и вертикальных напряжений в природном напряженном состоянии) будет Тогда коэффициент бокового распора (соотношение горизонтальных и вертикальных напряжений в природном напряженном состоянии) будет 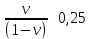 . .Это означает следующее. Если массив, сохраняющий упругое состояние, нагружен только одной активной силой – гравитацией (силой тяжести, собственным весом), то максимальными по величине в нем являются вертикальные напряжения, равные 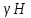 , а горизонтальные напряжения во всех направлениях равны и примерно в 4 раза меньше, чем вертикальные. , а горизонтальные напряжения во всех направлениях равны и примерно в 4 раза меньше, чем вертикальные. Геомеханикам для решения большинства практических задач достаточно знать соотношение между горизонтальными и вертикальными напряжениями в природном поле, которое называют коэффициентом бокового давления 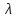 . В практике горного дела встречаются самые разнообразные виды природных напряженных состояний массивов. . В практике горного дела встречаются самые разнообразные виды природных напряженных состояний массивов.На месторождениях, где отсутствуют тектонические напряжения, максимальными по величине являются вертикальные гравитационные напряжения. Горизонтальные напряжения меньше вертикальных и обычно во всех направлениях в плане одинаковы. В данных случаях коэффициент бокового давления меньше единицы ( 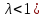 . Такое природное напряженное состояние массива наблюдается примерно на 30 % рудных месторождений, на всех угольных месторождениях. . Такое природное напряженное состояние массива наблюдается примерно на 30 % рудных месторождений, на всех угольных месторождениях. Многие осадочные породы после гидротермальных изменений, сопутствующих образованию колчеданных месторождений (серицитизации, хлоритизации), приобретают при большом давлении ярко выраженные пластические свойства. Пластичные породы (соли, глины) имеют коэффициент Пуассона 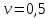 . .Если в формулу А. Н. Динника подставить коэффициент Пуассона 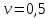 , тогда коэффициент бокового распора в пластичных массивах , тогда коэффициент бокового распора в пластичных массивах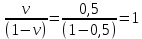 . .Это означает, что после перехода пород в пластичное состояние действующие в массиве природные горизонтальные напряжения становятся равными вертикальным. То есть во всех направления (вертикальном, в любых горизонтальных) давление одинаково ( 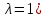 и равано и равано 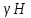 . .На большинстве рудных месторождений в массивах зарегистрировано наличие тектонических напряжений. Как правило, они превышают вертикальные, которые в этом случае являются минимальными главными напряжениями 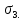 Причем в разных направлениях в плане действующие горизонтальные напряжения Причем в разных направлениях в плане действующие горизонтальные напряжения 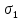 и и 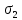 различаются, иногда в несколько раз. В таких случаях определяют два коэффициента бокового давления по направлениям действия главных напряжений: различаются, иногда в несколько раз. В таких случаях определяют два коэффициента бокового давления по направлениям действия главных напряжений: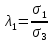 и и 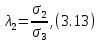 Часто направления действия главных нормативных напряжений связаны с основными элементами геологической структуры месторождения (направлениями падения и простирания залежей, главными: нарушениями). Признаки действия в массиве высоких тектонических напряжений: – хрупкое разрушение прочных пород в выработках и скважинах на небольшой глубине (известны случаи динамических нарушений со стрелянием пород даже на поверхности при проходке неглубоких траншей); – более высокая устойчивость выработок в менее прочных (и менее напряженных) породах; – повышение устойчивости кровли выработок по мере увеличения их пролета в частности, более высокая устойчивость очистных выработок пол сравнению с подготовительными. (Данное явление, на первый взгляд, кажется парадоксальным. Но как показала практика, является типичным и закономерным. С этим и связаны, с одной стороны, возможность возведения устойчивых большепролетных (до 50-70 м и более) подземных сооружений, с другой – образование при разработке месторождений труднообрушаемых зависаний подработанных пород на больших площадях); – при разработке месторождений в гористой местности наблюдается резкий рост проявлений горного давления при опускании ниже дна долин. (Это связано с тем, что в нагорной части месторождений на горизонтах выше дна долин (такие горизонты вскрываются штольнями) нет тектонических напряжений, а ниже дна долин они появляются в массиве). Из-за сложного геологического строения недр величину и направление действия тектонических напряжений можно установить только с помощью специальных измерений. Такие эксперименты проводятся во всем мире. Измерениями установлены следующие закономерности тектонических напряжений: – величины горизонтальных тектонических напряжений могут превышать вертикальное гравитационное давление налегающей толщи пород 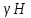 в 3 – 7 раз; в 3 – 7 раз;– тектонические напряжения в массиве горных пород распределяются неравномерно: даже в пределах одного месторождения могут встречаться участки с высоким и низшим уровнями горизонтальных напряжений; – наибольшие величины коэффициента большого давления 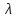 наблюдаются в верхних слоях земной коры, где ведутся горные работы; наблюдаются в верхних слоях земной коры, где ведутся горные работы;– на большой глубине (более 1,5 – 2,0 км) природное напряженное состояние массива приближается к гидростатическому (т. е. 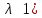 , так как уровень тектонических напряжений стремится к гравитационному давлению толщи вышележащих пород. , так как уровень тектонических напряжений стремится к гравитационному давлению толщи вышележащих пород.Тема 4. Напряженно деформированное состояние массива горных пород в зоне влияния горных выработок Лекция 7. Расчетные модели напряженно-деформированного состояния массива. Представление напряжений в полярной системе координат Лекция 8. Распределение напряжений вокруг горизонтальной выработки круглого сечения. Деформации выработок круглого сечения Лекция 7 4.1. Расчетные модели напряженно-деформированного состояния (НДС) Реальный массив горных пород представляет сложную среду, сформировавшуюся под влиянием геологических факторов. Массив неоднороден по составу, разбит трещинами на отдельные блоки, деформируется и разрушается под действием нагрузки, характеризуется различными физико-механическими свойствами. Для изучения и исследования характера протекающих процессов в массиве принимаются расчетные6 модели массива. В настоящее время применяются две группы моделей – модели сплошной среды и модели дискретной среды. Модели сплошной среды подразделяются на упругие, пластические, а также комбинированные упруго-пластичные, упруго-вязкие и др. Основные свойства этих моделей: сплошность, однородность, изотропность, деформируемость массива. Под сплошностью понимается заполненность материалом всего объема тела, ограниченного его поверхностью, включая бесконечно малые объемы в окрестностях каждой точки. Однородность – это одинаковость свойств среды в различных точках тела. Изотропность – одинаковость свойств среды во всех направлениях, проходящих через данную точку (если свойства материала различных в разных направлениях, он называется анизотропным). Деформируемость – это свойство материала изменять форму и размеры под действием внешних сил без разрывов и трещин (сопротивляемость материала изменению формы и размеров называют жесткостью). Наиболее широко применяется упругая модель массива. Главное в упругой модели – это линейная связь между напряжениями и деформациями 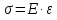 , где , где 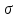 – напряжения, возникающие в массиве, – напряжения, возникающие в массиве, 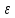 – относительная деформация, – относительная деформация, 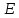 – модуль упругости породы, коэффициент поперечной деформации. – модуль упругости породы, коэффициент поперечной деформации. Применение упругой модели пород не требует обязательного восстановления начальной формы после снятия нагрузки, поэтому упругую модель массива называют еще линейно-деформируемой средой, а показатель 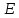 – модулем деформации. – модулем деформации.Вертикальные напряжения 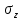 , обусловливаются весом вышележащих пород. , обусловливаются весом вышележащих пород.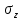 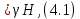 где 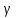 – удельный вес пород, – удельный вес пород, 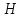 – глубина заложения выработки. – глубина заложения выработки.Горизонтальные напряжения 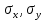 : :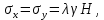 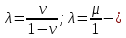 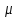 , , 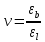 , , 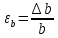 , , 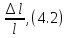 где 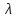 коэффициент горизонтального распора (бокового давления); коэффициент горизонтального распора (бокового давления); 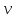 – коэффициент поперечных деформаций (коэффициент Пуассона); – коэффициент поперечных деформаций (коэффициент Пуассона); 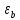 – относительная поперечная деформация; – относительная поперечная деформация; 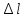 – абсолютная продольная деформация образцы длиной – абсолютная продольная деформация образцы длиной 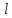 ; ; 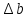 – абсолютная поперечная деформация образца шириной – абсолютная поперечная деформация образца шириной 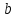 . .Для большинства горных пород коэффициент Пуассона можно принять 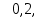 соответственно, коэффициент бокового распора соответственно, коэффициент бокового распора 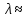 0,25. 0,25.В тех случаях, когда величина напряжений на контуре выработки превышает предел упругости, или, когда по поверхности структурного ослабления не выполняется условие специального предельного равновесия в массиве возникают не упругие – пластические деформации. Пластическая модель массива Пластичность – это свойство горных пород испытывать при нагружении необратимые (остаточные, пластические) деформации. При пластических деформациях массив горных пород теряет свою несущую способность не полностью, при этом разрушения не происходит. Вокруг выработки формируется зона неупругих деформаций, а площадь поперечного сечения выработки уменьшается – механизм деформирования рассматривается как пластическая модель массива. Пластические модели основаны на теории прочности Кулона-Мора. Основные положения модели: – пластические деформации (разрушения) происходят путем сдвига по площадкам скольжения; – сдвигу по площадке скольжения препятствует сцепление и трение; – пластичность (прочность) определяется величиной только максимальных и минимальных главных напряжений ( 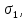 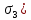 . Средние по величине главные напряжения ( . Средние по величине главные напряжения (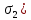 на прочность влияния не оказывают. на прочность влияния не оказывают.Условие прочности (пластичности) выражается уравнением 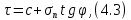 где 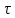 – сопротивление породы сдвигу; – сопротивление породы сдвигу; 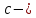 сцепление (сопротивление сдвигу, не зависящее от величины нормального давления); сцепление (сопротивление сдвигу, не зависящее от величины нормального давления); 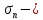 нормальные напряжения на площадке скольжения; нормальные напряжения на площадке скольжения; 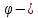 угол внутреннего трения породы. угол внутреннего трения породы.Если сдвигающее усилие меньше 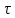 , то никаких деформаций не происходит. Условие (4.3) называется условием предельного состояния. , то никаких деформаций не происходит. Условие (4.3) называется условием предельного состояния.Если рассматривать горную выработку, то в такой среде вокруг выработки образуются две зоны: упругая и пластическая, причем граница раздела зон одновременно является границей раздела материалов с различными свойствами – исходного и разрушенного (модель исследована докт. техн. наук Ю. М. Либерманом). Раздельно-блочная модель массива как дискретной среды учитывает влияние на механические процессы структурного ослабления прочности пород, например, трещиноватости). Массив горных пород, лишенный сил сцепления между отдельными структурными блоками (оконтуренными макротрещинами протяженностью от десятков сантиметров до первых метров) рассматривают как сыпучий, если рассматриваемая область массива превышает в 3-4 раза максимальный размер структурного блока (по условию истечения сыпучего из отверстий). К такому массиву и такой рассматриваемой области применимы законы механики сыпучей среды. Напряженное состояние массива как сыпучей среды определяется по формулам: 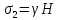 ; ; 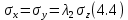 , ,где 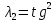 ( (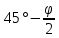 ) – коэффициент горизонтального распора для сыпучей среды; ) – коэффициент горизонтального распора для сыпучей среды; 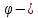 угол внутреннего трения сыпучего массива. угол внутреннего трения сыпучего массива.По характеру передачи усилий в дискретной среде они могут подразделяться на распорные и безраспорные. На рис. 4.1 показана модель и передача усилий между частицами распорной дискретной среды (песок, щебень и т. п.). На рис. 4.2 – модель и передача усилий между частицами в безраспорной (блочной) среде. 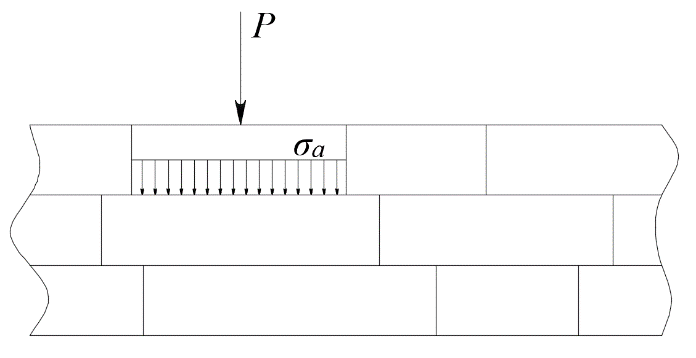  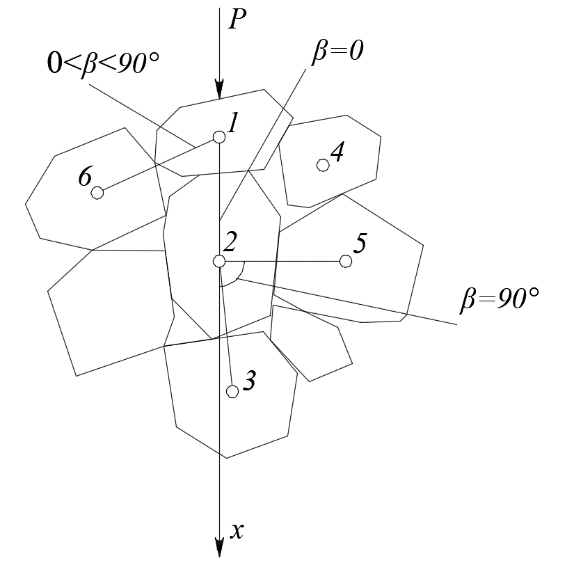 Рис. 4.2. Модель безраспорной дискретной среды  Рис. 4.1. Модель распорной дискретной среды Образующиеся вокруг выработки поля напряжений и смещений можно представить, как сумму начального поля напряжений и смещений нетронутого массива, т. е. до проведения выработки, и дополнительного поля напряжений и смещений, являющегося результатом выемки породы при проведении горных работ. Поскольку один из размеров для подготовительных и капитальных выработок (их длина), как правило, во много раз превышает два других, объемная задача по вычислению компонент напряжений и перемещений вокруг некоторой полости может быть сведена к плоской, т. е. к рассмотрению полей напряжений и перемещений лишь вокруг поперечного сечения выработки. |
