В.К.Багазеев Основы горной геомеханики. Курс лекций Екатеринбург, 2021 удк 622. 831 Рецензенты Зотеев О. В. Вандышев А. М
 Скачать 4.36 Mb. Скачать 4.36 Mb.
|
|
Тема 2. Напряжения и деформации в массиве пород Лекция 3. Основные определения напряжений в горных породах. Напряжения в наклонных сечениях при одноосной и двухосной нагрузке. Графическая интерпретация напряжений. Круги Мора. Лекция 4. Объемное напряженное состояние. Тензор напряжений. Лекция 3 2.1. Основные определения напряжений в горных породах В результате действия внешних сил на массив породы происходит смещение частиц массива, его деформация и разрушение. Под деформируемостью горных пород и массивов понимается их способность изменять свою форму и размеры в зависимости от силового воздействия. Деформацию горных пород подразделяют на упругую или упруго-вязкую, пластическую – вязко-пластическую и разрывную. При упругой деформации изменяется форма тела, но как только воздействие внешних сил прекращается, прежняя форма тела происходит без разрывов, но в отличие гот упругих деформаций пластические не восстанавливаются – они не обратимы: разрывные деформации сопровождаются нарушением сплошности – образуются трещины, массив разрушается. С началом действия внешних сил в массиве возникают внутренние силы, препятствующие деформации и разрушению массива. Величина внутренних сил в массиве, приходящихся на единицу площади, на которой они действуют, называется напряжением (рис. 2.1). 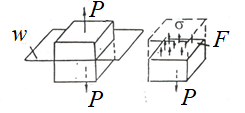  Рис. 2.1. Схема действия внутренних сил – напряжений: P – внешняя сила; F – площадь поперечного (перпендикулярного) сечения Напряжения характеризуются величи-ной и направлением, при этом напряжение, направленные перпендикулярно к рассмат-риваемой площадке, называют нормальны-ми (обозначают 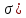 , а в плоскости площадки - касательными (обозначают τ): , а в плоскости площадки - касательными (обозначают τ):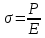 , ,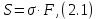 где 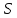 – равнодействующая внутренних сил (напряжений); P – внешняя сила; F – площадь действия внутренних сил. – равнодействующая внутренних сил (напряжений); P – внешняя сила; F – площадь действия внутренних сил.Единица измерения напряжений Па (Паскаль): 1 Па = 1Н/м2; 1 МПа = 106 Па = 0,102 кгс/см2 При действии наклонной силы 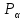 под углом под углом 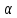 к поперечному сечению возникают напряжения к поперечному сечению возникают напряжения 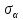 на наклонной площадке на наклонной площадке 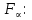 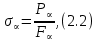 Разложим наклонную силу 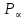 на две составляющие на две составляющие 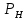 и T на (рис. 2.2) и T на (рис. 2.2)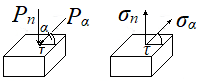 Соответствующие составляющие напряжения:  Рис. 2.2. Схема действия наклонной силы и соответствующих напряжений – нормальная 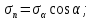 – касательная 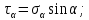 – полное напряжение 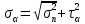 2.2. Напряжения по наклонным сечениям при одноосной нагрузке Одноосной нагрузкой называется такая нагрузка, при которой внешние силы расположены по одной линии. Для правильной оценки напряженного состояния реального массива горных пород необходимо знать напряжения по площадкам, наклонным к оси действия нагрузки. Рассмотрим элементарный блок породы сечением S, находящийся под воздействием двух противоположно направленных вдоль оси блока сил P. Требуется вычислить напряжения, возникающие по наклонному сечению. Для этого рассечем блок плоскостью mn, наклонной под углом 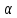 к нормальному сечению. Внешняя нормаль Nк проведенному сечению будет составлять с осью блока тоже угол α. Отбросим верхнюю часть. Для того чтобы нижняя часть находилась в равновесии, необходимо приложить к ней силы, параллельные оси блока (рис. 2.3). к нормальному сечению. Внешняя нормаль Nк проведенному сечению будет составлять с осью блока тоже угол α. Отбросим верхнюю часть. Для того чтобы нижняя часть находилась в равновесии, необходимо приложить к ней силы, параллельные оси блока (рис. 2.3).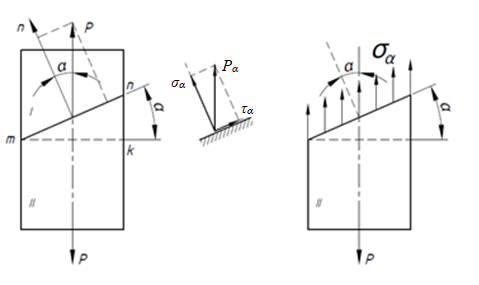 Условие равновесия нижней части блока будет: 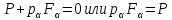 , , Рис. 2.3. Напряжения в элементарном блоке (при одноосной нагрузке P) Отсюда получим, что напряжение 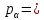 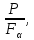 где 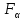 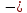 площадь наклонного сечения. площадь наклонного сечения.Из рисунка следует, что площадь наклонного сечения 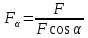 , , где 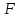 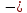 площадь нормального сечения. площадь нормального сечения.Подставляя значение 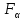 в формулу (3.2.1), получаем: в формулу (3.2.1), получаем: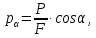 Учитывая, что 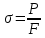 , находим: , находим: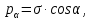 Раскладывая полное напряжение на нормальное и касательное (составляющие напряжения), получим: 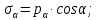 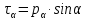 Подставляя значение 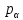 по формуле (3.2.3), получим: по формуле (3.2.3), получим: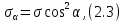 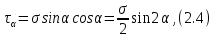 Нормальное напряжение 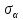 на наклонной под углом α площадке равно, напряжению на наклонной под углом α площадке равно, напряжению 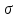 на площадке F перпендикулярной (нормальной) к оси действие силы P, умноженному на на площадке F перпендикулярной (нормальной) к оси действие силы P, умноженному на 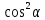 . .Касательное напряжение 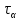 на наклонной под углом α равно, половине напряжения на наклонной под углом α равно, половине напряжения 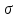 равно, половине напряжения σ на площадке F, перпендикулярной (нормальной) к оси действия силы P, умноженному на равно, половине напряжения σ на площадке F, перпендикулярной (нормальной) к оси действия силы P, умноженному на 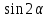 . .График зависимости напряжений на наклонной площадке приводится на рис. 2.4. 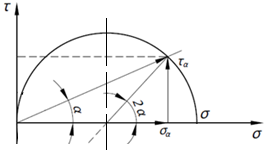 Рис. 2.4. Напряжения на наклонных площадках при одноосной нагрузке Проследим, как изменяются составляющие напряжения с изменением угла наклона площади. При возрастании угла 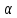 от 0 до 90 от 0 до 90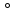 нормальное напряжение по площадке будет уменьшаться от значения нормальное напряжение по площадке будет уменьшаться от значения 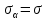 до значения до значения 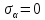 . Касательные напряжения с изменением угла . Касательные напряжения с изменением угла 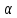 от 0 до 45 от 0 до 45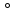 возрастают от значения возрастают от значения 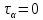 до значения до значения 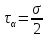 , а затем убывают до , а затем убывают до 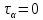 при угле при угле 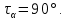 Следовательно, при растяжении или сжатии наибольшие нормальные напряжения возникают по площадкам, перпендикулярным к оси блока, а наибольшие касательные напряжения по площадкам, расположенным под углом 45 Следовательно, при растяжении или сжатии наибольшие нормальные напряжения возникают по площадкам, перпендикулярным к оси блока, а наибольшие касательные напряжения по площадкам, расположенным под углом 45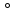 к оси блока к оси. Наибольшее касательное напряжение равно половине наибольших нормальных напряжений. к оси блока к оси. Наибольшее касательное напряжение равно половине наибольших нормальных напряжений.На площадке по углом 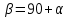 : :  2.3. Напряжения в наклонных сечениях при плоском напряженном состоянии При действии нагрузки в двух взаимно перпендикулярных направлениях (в одной плоскости) возникает плоское напряженное состояние. Рассмотрим призматический брус, на боковые грани которого действуют напряжения 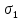 и и 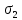 (рис. 2.5). (рис. 2.5). 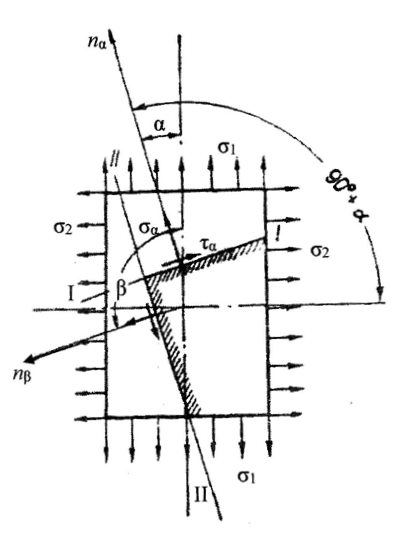 Оба напряжения будем считать растягивающими, причем Оба напряжения будем считать растягивающими, причем 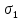 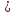 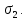 Требуется определить нормальные и касательные напряжения по наклонным сечениям: I – I – под углом Требуется определить нормальные и касательные напряжения по наклонным сечениям: I – I – под углом 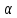 и сечение II – II – под углом и сечение II – II – под углом 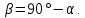 На каждой площадке под действием напряжений На каждой площадке под действием напряжений 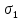 и и 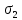 (с учетом принципа независимости действия сил) возникают напряжения (по ранее полученным формулам 2.3., 2.4): (с учетом принципа независимости действия сил) возникают напряжения (по ранее полученным формулам 2.3., 2.4): Рис. 2.5. Напряжения в брусе на площадке I – I – под углом 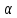 получим получим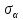 = =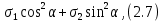 , ,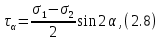 на площадке II – II – под углом 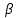 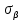 = =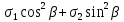 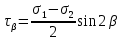 Для нашего случая угол 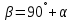 . Следовательно . Следовательно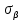 = =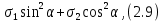 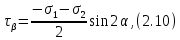 Из полученных формул для напряжений, действующих по взаимно перпендикулярным сечениям, можно вывести два важных свойства: 1) складывая выражения (2.7) и (2.9), получим: 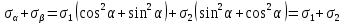 , ,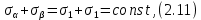 т.е. сумма нормальных напряжений по двум взаимно перпендикулярным сечениям постоянна; 2) сопоставляя формулы (2.8) и (2.10), получим: 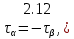 т.е. касательные напряжения по двум взаимно перпендикулярным сечениям равны по величине и противоположны по знаку. Это свойство обычно называют законом парности касательных напряжений (касательные напряжения в двух взаимно перпендикулярных площадках, перпендикулярны их общему ребру и равны по модулю). Для определения наибольшего значения нормального напряжения возьмем производную от выражения (2.7) и приравняем ее нулю. Тогда: 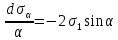 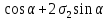 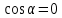 . .Так как 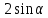 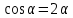 , после преобразования получим: , после преобразования получим: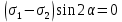 Из этого выражения следует: при 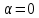 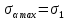 при 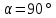 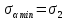 Наибольшее и наименьшее нормальные выражения, действующие по взаимно перпендикулярным сечениям, равны соответственно 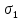 и и 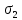 . Наибольшее значение касательных напряжений будет при . Наибольшее значение касательных напряжений будет при 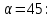 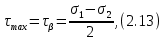 . .2.4. Графическая интерпретация напряжений. Круги Мора Аналитическая зависимость касательных от нормальных напряжений при плоском напряженном состоянии выражается формулами: 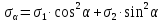 , ,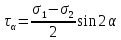 , ,которые после преобразований (с учетом 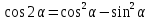 , приводятся к виду , приводятся к виду 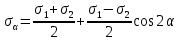 , (3.14) , (3.14)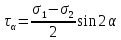 . .Эти зависимости представляют уравнение окружности в параметрической форме в системе координат 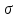 и и 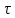 . Таким образом, напряженное состояние на площадке I – I можно представить графически также как и при одноосной нагрузке в виде окружности, координаты точек которой определяют напряжения на соответствующей площадке, а угол . Таким образом, напряженное состояние на площадке I – I можно представить графически также как и при одноосной нагрузке в виде окружности, координаты точек которой определяют напряжения на соответствующей площадке, а угол 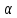 определяет ориентацию площадки. Центр окружности находится на расстоянии определяет ориентацию площадки. Центр окружности находится на расстоянии 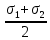 от нач,ала координат по оси от нач,ала координат по оси 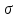 . Радиус окружности равен . Радиус окружности равен 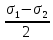 . .Эта окружность носит название круг Мора или круговой диаграммой напряженного состояния. Каждая площадка имеет координаты 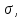 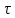 . Точки соответствующие двум взаимно перпендикулярным площадкам, на круге напряжений расположены диаметрально противоположно. Следовательно, зная напряжения на двух взаимно перпендикулярных площадках можно построить окружность. Координаты вертикальной площадки ( . Точки соответствующие двум взаимно перпендикулярным площадкам, на круге напряжений расположены диаметрально противоположно. Следовательно, зная напряжения на двух взаимно перпендикулярных площадках можно построить окружность. Координаты вертикальной площадки (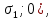 горизонтальной ( горизонтальной (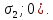 В системе координат 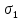 , , 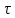 точка В соответствует вертикальной площадке, точка С - горизонтальной площадке (рис. 2.6). точка В соответствует вертикальной площадке, точка С - горизонтальной площадке (рис. 2.6).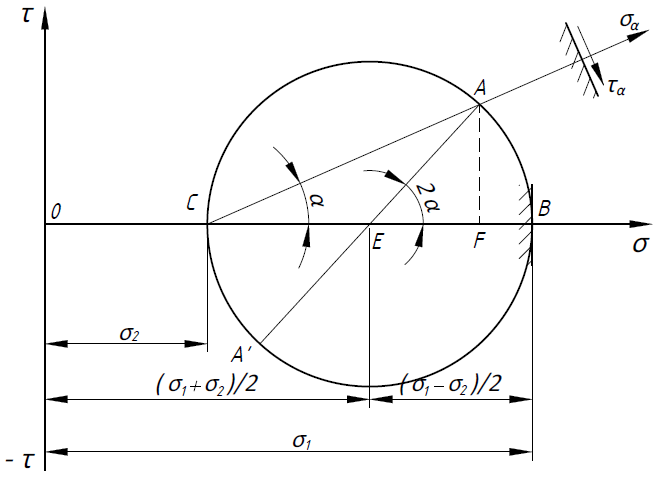 Рис. 2.6. Круговая диаграмма напряженного состояния Точка А соответствует площадке, нормаль к которой расположена под углом α к горизонтали. Порядок построения круговой диаграммы (рис.2.6): принимаем прямоугольную систему координат (σ, τ) так, чтобы ось абсцисс была параллельна большему из главных напряжений; на оси абсцисс от начала координат отложить отрезки, численно равные главным напряжениям σ1 и σ2 и на их разности, как на диаметре построить окружность; из крайней левой точки С окружности провести луч, параллельный нормали к площадке α. Не трудно показать, что координаты точки А пересечения этого луча с окружностью соответствуют напряжением на площадке под углом α: 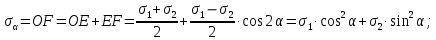 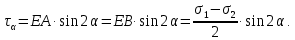 Аналогично можно показать, что координаты точки А' соответствуют величине напряжений на площадке под углом β = 90 + α: 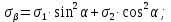 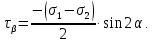 Если заданы площадки общего положения, по которым действуют нормальные и касательные напряжения, определяемые при том или ином методе расчета, то координаты точек, соответствующих вертикальным и горизонтальным площадкам соответственно (σх, τух), горизонтальной (σу, τух) (рис. 4.9, а). Для построения круга напряжений примем, что в данном случае σх > σу. Центр круга имеет координату 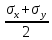 , радиус круга равен , радиус круга равен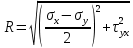 Лекция 4 2.5. Объемное напряженное состояние. Тензор напряжений 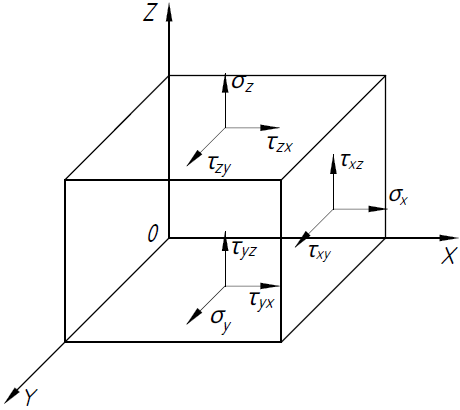 В естественных условиях горные породы находятся под действием сил, действующих не только в одном или двух направлениях, чаще всего силы действуют по трем направлениям на трех взаимно перпендикулярных площадках. В этом случае создается объемное (трехосное) напряженное состояние элемента массива, при котором на каждой площадке действует одно нормальное и два касательных напряжения. Разместим элемент в координатной сетке х, у, z и обозначим напряжения индексами (рис. 2.7). В естественных условиях горные породы находятся под действием сил, действующих не только в одном или двух направлениях, чаще всего силы действуют по трем направлениям на трех взаимно перпендикулярных площадках. В этом случае создается объемное (трехосное) напряженное состояние элемента массива, при котором на каждой площадке действует одно нормальное и два касательных напряжения. Разместим элемент в координатной сетке х, у, z и обозначим напряжения индексами (рис. 2.7).Рис. 2.7. Компоненты напряжений при объемном напряженном состоянии Нормальные напряжения σх, σу, σz - индекс указывает направление оси, параллельно которой действует данное напряжение. Касательные напряжения 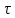 обозначаются двумя индексами: первый – направление нормали к площадке (адрес площадки), второй - направление действия, например, τzу – касательное напряжение на площадке с нормалью параллельной z, направленное по оси у. обозначаются двумя индексами: первый – направление нормали к площадке (адрес площадки), второй - направление действия, например, τzу – касательное напряжение на площадке с нормалью параллельной z, направленное по оси у. Для удобства оперирования и вычислений расположим все напряжения в форме таблицы-матрицы размерами три строки и три столбца элементов напряжений - Tσ (3 х 3): 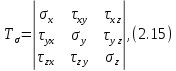 Здесь в первой строке расположены элементы, имеющие направление параллельное оси х, во второй – параллельное оси у, в третьей – оси z. Таким образом каждая строка матрицы содержит компоненты полного напряжения, действующие на одной из трех граней. В этом случае нормальные напряжения расположены по главной диагонали, а одинаковые по величине касательные напряжения – симметрично относительно ее. Эту симметричную матрицу называют тензором напряжений. (Тензорное исчисление широко применяется в механике, гидравлике, газодинамике и других областях науки). У тензора имеется замечательное свойство – независимость (инвариантность) от принятой системы координат. Если вместо исходной системы осей (х, у, z) выбрать новую систему (α, β, γ), компоненты тензора изменятся. Однако тензор напряжений, как количественная характеристика напряженного состояния, остается тем же. В любой точке массива всегда можно провести три взаимно перпендикулярные площадки, в которых отсутствуют касательные напряжения, а действуют только нормальные напряжения σ1, σ2, σ3. Таким образом количество независимых компонентов, характеризующих напряженное состояние уменьшается до трех. Тензор напряжений в этом случае, не меняя своей величины (инвариантный тензор) принимает вид: 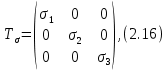 Площадки, по которым касательные напряжения отсутствуют, называются главными. Нормальные напряжения, действующие на этих площадках, называются главными напряжениями. Они принимают экстремальные значения. Главные напряжения нумеруют в порядке убывания величины напряжения в алгебраическом смысле 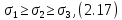 Определение главных напряжений является необходимым этапом при расчетах на прочность в общем случае напряженного состояния. В экспериментальных исследованиях часто объемное напряженное состояние сводится к условиям плоской деформации или плоскодеформированного напряженного состояния, при котором все три компоненты главных напряжений отличны от 0, но по одной из главных осей, перпендикулярной к плоскости исследуемого сечения, нет возможности перемещений, т.е. деформации равны 0. В условиях плосконапряженного или плоскодеформированного состояния значительно упрощается переход от значений компонент напряжений в декартовых осях к главным напряжениям: 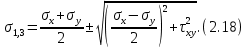 Угол α между осью Х и направлением действия максимального сжимающего напряжения 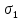 можно определить следующим образом: можно определить следующим образом: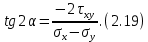 В соотношении (2.19) считается, что угол α отсчитывается от оси Х к оси σ1 против часовой стрелки. Обратный переход от главных напряжений к напряжениям в декартовых осях осуществляется по формулам: 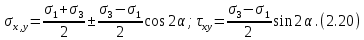 Формулы (3.12) и (3.13) записаны для плоскости х – у, аналогично можно записать и для двух других плоскостей (y – z;z – x). В дальнейшем при исследовании напряженного состояния в точке необходимо определять главные напряжения, потому что расчеты на прочность построены на основании главных напряжений. Необходимо отметить, что изначально в геомеханике сжимающие напряжения считались положительными. При этом касательные напряжения считались положительными в том случае, если они стремились развернуть тело по часовой стрелке. Соглашение о соотношении величин главных нормальных напряжений при этом 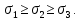 Таким образом, напряжением наибольшего сжатия в этой системе знаков являлось напряжение Таким образом, напряжением наибольшего сжатия в этой системе знаков являлось напряжение 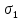 , а напряжение , а напряжение 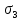 - напряжением наименьшего сжатия или наибольшего растяжения. Такое правило знаков напряжений достаточно широко распространено в литературе, особенно в работах, посвященных методу предельного равновесия, механике грунтов, устойчивости бортов карьеров, отвалов, дамб и пр. - напряжением наименьшего сжатия или наибольшего растяжения. Такое правило знаков напряжений достаточно широко распространено в литературе, особенно в работах, посвященных методу предельного равновесия, механике грунтов, устойчивости бортов карьеров, отвалов, дамб и пр. Вместе с тем в технической литературе возможно и противоположные обозначения напряжений (это следует иметь ввиду). Тема 3. Предельно-напряженное состояние и разрушение пород Лекция 5. Теории прочности пород. Основные уравнения предельного равновесия деформируемости пород. Лекция 6. Природное напряженное состояние массива Лекция 5 |
