В.К.Багазеев Основы горной геомеханики. Курс лекций Екатеринбург, 2021 удк 622. 831 Рецензенты Зотеев О. В. Вандышев А. М
 Скачать 4.36 Mb. Скачать 4.36 Mb.
|
|
3.1. Теории прочности пород Разрушение горных пород – это нарушение сплошности природных структур горных пород (минеральных агрегатов, массивов горных пород) под действием естественных и искусственных сил. Механическое разрушение бывает при сжатии, при изгибе, при кручении и т. п. Различают два основных вида разрушения горных пород: – хрупкий – происходящий практически без изменения объема и формы тела или при его незначительной упругой деформации; пластический, пластический, которому предшествуют течение, – пластический, которому предшествует течение, пластическое скольжение и другие явления. Пластическое разрушение может наступить после того, как приложенные напряжения превысят предел текучести при значительных изменениях объема и формы тела. Классификация разрушения горных пород на виды несет в себе определенную долю условности. На практике могут встречаться задачи когда горные породы деформируются и разрушаются как тела упругие и как тела пластические в одинаковой мере. В таких случаях может возникнуть необходимость рассматривать процесс как упруго-пластический. Любому виду разрушения предшествует предельно-напряженное состояние, при котором малейшее увеличение действующих сил повлечет разрушение. Для хрупких материалов за предельное состояние принято считать начало разрушения, для пластичных – состояние, соответствующее началу развития массовых остаточных (пластических) деформаций. Существует целый ряд теорий и гипотез разрушения горных пород, их еще называют теориями прочности, которые можно объединить в несколько групп. 1. Теории прочности, предполагающие в качестве критерия разрушения наибольшие напряжения. Согласно этим теориям, разрушение тела наступает в том случае, если наибольшее, нормальное напряжение достигает какого-то предела 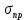 (Галилей) или если наибольшие касательные напряжения будут равны пределу прочности материала на сдвиг (Галилей) или если наибольшие касательные напряжения будут равны пределу прочности материала на сдвиг 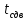 (Кулон). Эти теории не учитывают совокупности факторов, приводящих к разрушению, не получают экспериментального подтверждения. Материал может разрушиться в одном случае в виде разрыва, в другом – в виде сдвига, хотя по характеру силовая нагрузка в обоих случаях одинакова (сжимающая). (Кулон). Эти теории не учитывают совокупности факторов, приводящих к разрушению, не получают экспериментального подтверждения. Материал может разрушиться в одном случае в виде разрыва, в другом – в виде сдвига, хотя по характеру силовая нагрузка в обоих случаях одинакова (сжимающая).2. Теории прочности, согласно которым разрушение твердого тела наступает, когда наибольшие относительные деформации достигнут определенного предельного значения. 3. Согласно энергетической теории (К. Максвелл), прочность тела пропорциональна работе, затраченной на изменение его формы при деформации. При этом предполагается, что объем тела остается неизменным. 4. Большое распространение получила теория прочности Мора (О. Мор, Како), согласно которой разрушение твердого тела наступает при определенном соотношении между нормальными и касательными напряжениями в данной площадке. 5. За последние годы стала развиваться статистическая теория прочности твердых тел (В. Вейбулл, Т. А. Конторова, Я. И. Френкель), которая исходит из предположения, что прочность тела определяется прочностью его наиболее слабого участка. Наибольшеераспространение среди теорий хрупкого разрушенияполучила Теория разрушения Гриффитса. Согласно этой теории, твердое тело разбито серией структурных дефектов. При приложении нагрузки напряжения в твердом теле распределяются неравномерно, концентрируясь на концах трещин. Если величина напряжений в зоне концентрации соизмерима с пределом прочности пород, то происходит раскрытие трещин, перераспределение напряжений, и зона концентрации напряжений перераспределяется на концы вновь развившейся трещины. В зависимости от соотношения напряжений в массиве пород и прочностных характеристик массива процесс развития дефектов может носить затухающий характер или привести к вырождению трещин в общую поверхность разрушения с полной потерей прочности и сплошности образца. Таким образом, теория Гриффитса описывает процесс разрушения горных пород и объясняет эффект «памяти» - наследственности пород. Наибольшее же количество теорий (критериев) прочности, используемых в геомеханике, описывают пластическое разрушение материала. В инженерных расчетах чаше используют так называемые феноменологические теории прочности пород, базирующиеся на различных теоретических предпосылках, объясняющих нарушение предельного устойчивого состояния горных пород. Все эти теории сводятся к приведению объемного напряженного состояния горных пород к пределу прочности на одноосное сжатие. Всего существует более 150 теорий прочности. Рассмотрим наиболее распространенные. Теория максимальных нормальных напряжений (гипотеза Галилея). Согласно этой теории, разрушение горных пород происходит в том случае, если одна из компонент главных напряжений превысит предел прочности горных пород на сжатие или растяжение, не зависящий от вида напряженного состояния: 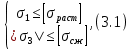 где 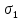 , , 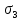 – максимальное и минимальное главные напряжения в массиве пород, МПа. – максимальное и минимальное главные напряжения в массиве пород, МПа.Недостатком данной теории является то, что она учитывает только одну из компонент тензора напряжений, хотя ее положения находят качественное подтверждение в испытаниях на растяжение и кручение образцов из весьма хрупкого материала. В геомеханике эта теория используется при расчете параметров конструктивных элементов систем разработки, находящихся в условиях одноосного сжатия или растяжения, например, опорные целики при камерно-столбовой системе разработки. Теория предельных линейных деформаций (гипотеза Мариотта). Согласно этой теории, нарушение устойчивости массива в процессе горных работ происходит в случае, если деформации массива превысят значения предельных упругих деформаций сжатия или растяжения, не зависящих от вида напряженного состояния: 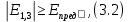 Недостатком данной теории является то, что предельные упругие теория дает удовлетворительные результаты, но для пластичных она не деформации в условиях объемного напряженного состояния зависят от бокового зажима пород. Эксперименты показывают, что для хрупких материалов эта подтверждается. Теория максимальных касательных напряжений (гипотеза Кулона-Треска). Согласно данной теории, пластические деформации в массиве возникают при достижении касательными напряжениями предельных значений, которые не зависят от вида напряженного состояния: 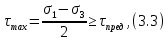 Расчеты по данной теории дают достаточную сходимость для пластичных горных пород. В хрупких породах применение данной теории неприемлемо. Энергетическая теория прочности К. Максвелла постулирует, что прочность тела пропорциональна работе, затраченной на изменение его формы при деформировании. При этом предполагается, что объем тела остается неизменным. В основу критерия разрушения положена разность работы сил, приложенных к элементу, направленной на разрушение и деформирование элемента. Эта теория получила подтверждение в условиях работы элементов конструкции на растяжение, в горном деле широкого распространения не получила. Статистическая теория прочности В Вейбулла, Т. А.Кантолрова, Я. И. Френкеля получила широкое развитие в последние годы. Теория, в общем, исходит из предположения, что прочность тела в целом определяется прочность наиболее слабого участка, по принципу «где слабо – там и рвется», и поэтому для определения условий разрушения необходимо сопоставлять прочностные характеристики по поверхностям ослабления со значением напряжений на этих поверхностях. Согласно перечисленным теориям, дать определения условий и построения условий и построения поверхности разрушения образ необходимо знать лишь результаты испытан6ия пород в условиях одноосного сжатия или растяжения. 3.2. Основные уравнения предельного равновесия горных пород. Теория прочности Мора Теория прочности О. Мора (предложена в 1882 г.) широко применяется для описания условий разрушения горных пород. При этом принято, что условия разрушения определяются значениями наибольшего и наименьшего главных напряжений. Согласно теории прочности О. Мора, разрушения происходят по площадкам сдвига, где касательные напряжения больше критических (допускаемых) напряжений 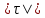 , а также в случае, если нормальные растягивающие напряжения превысят предел прочности на растяжение , а также в случае, если нормальные растягивающие напряжения превысят предел прочности на растяжение 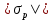 при отсутствии касательных напряжений. при отсутствии касательных напряжений.Условием предельного равновесия на площадке является закон прочности Кулона-Мора для связных пород 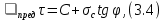 для сыпучих пород 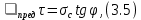 где 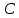 – сцепление, параметр, соответствующий прочности грунта при нулевом значении нормального напряжения на площадке сдвига; – сцепление, параметр, соответствующий прочности грунта при нулевом значении нормального напряжения на площадке сдвига;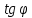 – коэффициент пропорциональности, равный тангенсу угла внутреннего – коэффициент пропорциональности, равный тангенсу угла внутреннеготрения пород; 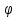 – угол внутреннего трения пород; – угол внутреннего трения пород;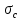 – эффективные нормальные напряжения на площадке среза (эффективные – эффективные нормальные напряжения на площадке среза (эффективные – значит без учета парового давления). График сопротивления пород сдвигу (рис. 3.1) называют графиком прочности пород или диаграммой прочности. 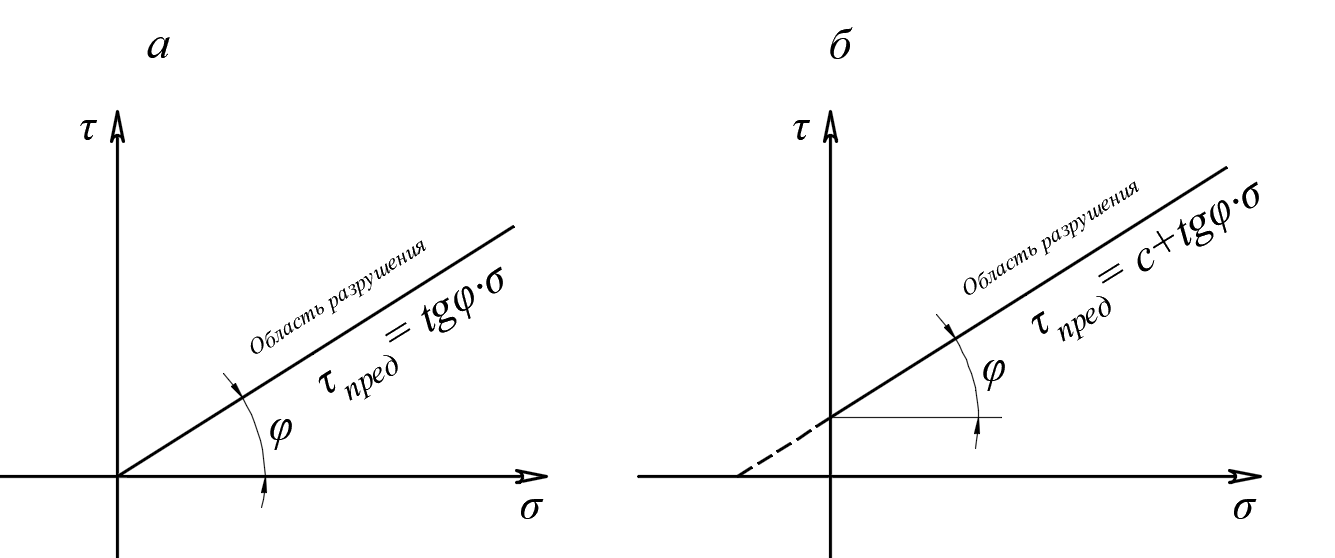 Рис.3.1. График сопротивления пород сдвигу: а – сыпучих; б – связных Если в условие равновесия (3.4; 3.5) подставим значения по формулам (2.7,, 2.10) 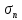 = =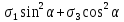 ; ;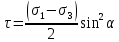 , ,то становится очевидным, что с изменением угла наклона площадки изменяется и условие равновесия. Отразим это графически с помощью кругов Мора (рис. 3.2). BF – линия, ограничивающая область предельных напряжений (при которых еще не происходит разрушение), а координаты точки M ( 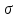 , , 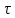 ) являются параметрами предельного напряженного состояния на площадке под углом ) являются параметрами предельного напряженного состояния на площадке под углом 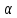 . .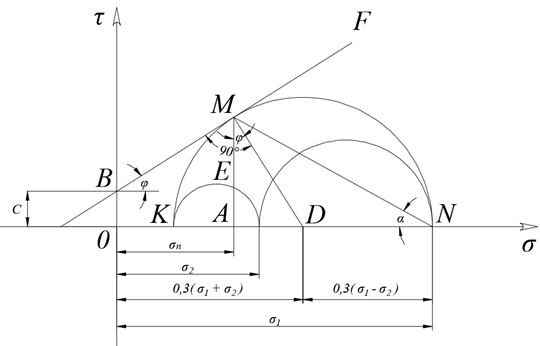 Рис. 3.2. Схема для расчета нормальных и сдвиговых напряжений Из треугольника ВМЕ 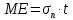 g g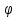 , тогда , тогда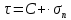 , ,по построению кругов Мора угол 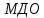 = = 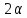 , из треугольника , из треугольника 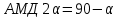 или или 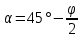 , таким образом, координата точки , таким образом, координата точки 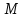 ( (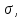 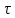 ) есть параметры предельного равновесия на площадке к главному напряжению ) есть параметры предельного равновесия на площадке к главному напряжению 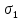 под углом под углом 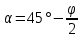 ; ;Из треугольника АМД 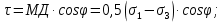 тогда 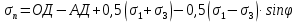 . .Подставим значения 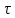 и и 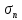 в уравнение: в уравнение: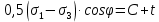 g g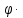 0,5[ 0,5[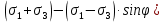 , ,после преобразований 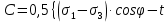 g g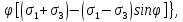 , ,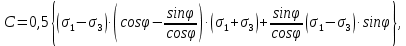 , ,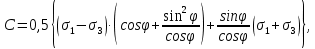 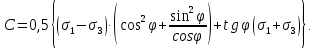 Получим: 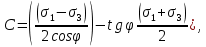 или 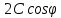 = =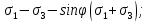 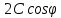 = =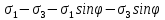 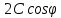 = =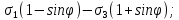 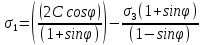 ; ;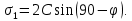 Известно, что 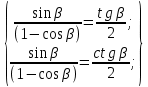 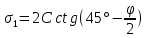 При одноосном сжатии, когда 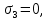 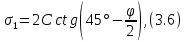 Нетрудно догадаться, что = 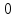 в случае, если нет бокового отпора пород, т. е. это обнаженная поверхность; если в случае, если нет бокового отпора пород, т. е. это обнаженная поверхность; если 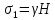 и и 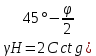 ), то высота свободной поверхности ), то высота свободной поверхности 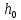 , называемой еще высотой вертикального откоса , называемой еще высотой вертикального откоса 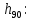 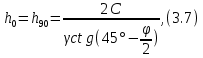 Если линию BF продолжить до пересечения с осью абсцисс, то полученную точку 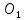 можно рассматривать как начало условных (приведенных) координат. В этом случае отрезок можно рассматривать как начало условных (приведенных) координат. В этом случае отрезок 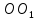 (см. рис. 4.3) характеризует собой временное сопротивление пород растяжению, а нормальное приведенное напряжение (см. рис. 4.3) характеризует собой временное сопротивление пород растяжению, а нормальное приведенное напряжение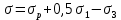 , ,уравнение предельного равновесия 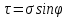 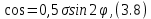 3.3. Деформируемость пород. Тензор деформаций Упругие деформации массива пород, соответствующие закону Гука характерны лишь для малых значений. Дальнейшее деформирование приводит или к хрупкому разрушению, или к потере пропорциональности между напряжениями и деформациями, а также к появлению пластических (необратимых) деформаций. В области упругих деформаций деформированное состояние точки в массиве можно записать в виде тензора деформаций 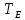 . .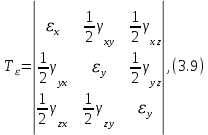 где 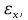 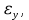 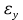 – линейные деформации в направлении координат; – линейные деформации в направлении координат; 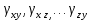 – угловые деформации (рис. 1.3) – угловые деформации (рис. 1.3)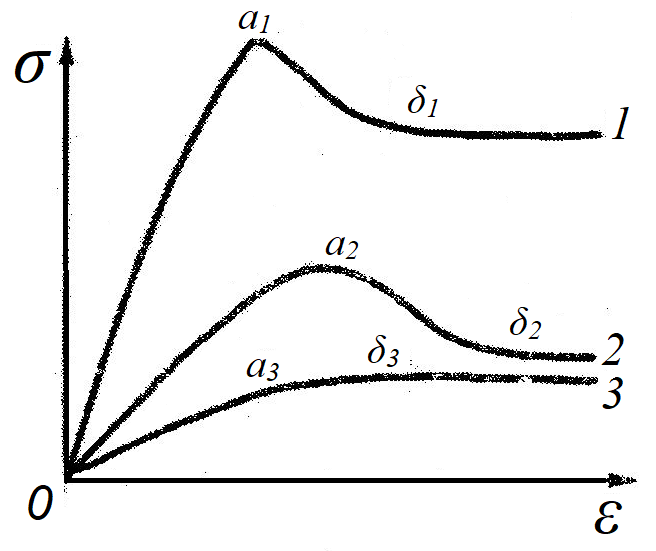 Наиболее характерными видами деформации и разрушения горных пород являются растяжения с последующим разрывом (отрывом) и сдвиг, приводящий к срезу (сколу). На рис. 4.4. представлены графики деформаций при испытаниях горных пород при сдвиге. Наиболее характерными видами деформации и разрушения горных пород являются растяжения с последующим разрывом (отрывом) и сдвиг, приводящий к срезу (сколу). На рис. 4.4. представлены графики деформаций при испытаниях горных пород при сдвиге.Рис. 4.4. Диаграмма «Напряжение-деформация» при испытании пород различной структурной нарушенности: 1 – деформация монолитного образца; 2 – деформация образца с несколькими системами трещин (более двух); 3 – деформация образца с выраженной структурной анизотропией (в простейшем случае с одной плоскостью ослабления) На участках деформации образцов определяются характером структурной неоднородности. Для монолитного образца, отличающегося значительными силами сцепления между частицами (между зернами и цементом, например), характерно существенное нарастание напряжений при сравнительно небольших деформациях (участок 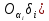 . По достижении предела прочности (точка . По достижении предела прочности (точка 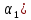 образец разрушается, в нем формируется зона или поверхность сдвига (участок образец разрушается, в нем формируется зона или поверхность сдвига (участок 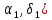 , по которой в дальнейшем и происходит сдвиг с постоянной скоростью (участок за точкой , по которой в дальнейшем и происходит сдвиг с постоянной скоростью (участок за точкой 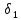 ). ).Деформирование образца, структурно раздробленного несколькими системами трещин, происходит по аналогичной схеме (график 2). Разница лишь в том, что прочность трещиноватого образца ниже и предельное состояние достигается при меньших нагрузках. Характер деформирования образца, содержащего выраженную структурную анизотропию (поверхность ослабления), отличен от предыдущих. Здесь деформация сдвига с самого начала реализуется по имеющейся поверхности и после преодоления сил сцепления (между поверхностями трещин) стабилизируется и продолжается с постоянной скоростью. Таким образом графики 1 и 2 иллюстрируют отмеченное ранее косвенное влияние структурной раздробленности горных пород на их деформационные свойства, проявляющееся через снижение прочности массива. График 3 иллюстрирует непосредственное влияние разрывных нарушений на деформационные характеристики массива пород. Сопоставляя эти данные с выделенными ранее масштабными уровнями структурной раздробленности массивов пород, можно отметить, что для наиболее распространенных объектов горной геомеханики (с линейными параметрами в интервале 101-102 м) графики 1-3 отражают влияние структурной неоднородности соответственно III-I масштабных уровней. Для определения зависимостей устойчивости горизонтальных обнажений пород от параметров трещиноватости (сцепление по трещинам, расстояния между различными системами трещин, углов наклона трещин) выполнены специальные исследования. Полученные данные использовались для составления графиков и их аппроксимации в виде функциональных выражений. Поскольку графики и соответствующие им функциональные зависимости получены в относительных величинах, эти результаты могут быть использованы для различных условий. Лекция 6 |
