В.К.Багазеев Основы горной геомеханики. Курс лекций Екатеринбург, 2021 удк 622. 831 Рецензенты Зотеев О. В. Вандышев А. М
 Скачать 4.36 Mb. Скачать 4.36 Mb.
|
|
Тема 7. Физическое моделирование геомеханических процессов Лекция 15 7.1. Общие сведения Моделирование как метод исследования широко используют в различных областях современного естествознания и техники: аэромеханике, гидравлике, теплотехнике, самолето- и ракетостроении, различных областях машиностроения, гидротехническом строительстве и т. д. Модели – это инженерные представления, которые могут быть материализованы в виде физических моделей или сформулированы математически. Модель – это система, находящаяся в объективном соответствии с исследуемым объектом (явлением, физическим процессом), отражающим наиболее существенные свойства и информацию о самом объекте (явлении, процессе). Исходя из этого по принципам, на которых основано моделирование, различают моделирование двух видов: физическое и математическое. Физическое моделирование предусматривает воссоздание в физической модели тех же самых физических полей, что действуют и в объекте натуры, лишь измененных по своим абсолютным значениям в соответствии с масштабом моделирования. Одним из основных преимуществ физического моделирования является возможность осуществления прямых наблюдений за моделируемыми процессами и явлениями, иногда это преимущество является решающим. В физическом моделировании выделяется аналоговое моделирование, которое предусматривает замену в модели по сравнению с натурой одних физических полей другими, например замену натурного поля механических напряжений электрическим полем в модели или замену поля механических напряжений картиной оптической анизотропии в оптически чувствительных прозрачных материалах. Таким образом, на аналоговых моделях изучают закономерности явлений и процессов, протекающих в натурных объектах, используя математическую аналогию различных по физической природе процессов, т. е. математическую тождественность основных законов, совпадение дифференциальных уравнений, описывающих эти процессы. В отличие от физического математическое моделирование предусматривает построение некоторых идеализированных схем или, другими словами, математических моделей исследуемых процессов или явлений и их исследование аналитическими методами. Исходя из этого методы математического моделирования относят к теоретическим методам исследования. Такая точка зрения доминирует в геомеханике. Моделирование получило широкое развитие в геомеханике вследствие ряда объективных обстоятельств. Как уже указывалось, массив горных пород является весьма сложной средой, которая к тому же находится под одновременным воздействием большого числа факторов как естественного, так и техногенного происхождения. К этому следует добавить, что в натурных условиях, обычно весьма ограничены возможности варьирования параметрами системы, технологией и последовательностью ведения горных работ, тогда как при моделировании можно проследить влияние основных параметров в самых широких пределах. Физическое моделирование бывает двух видов: с увеличением и с уменьшением масштаба системы. В геомеханике, изучающей, как правило, объекты весьма больших размеров, применяют моделирование второго рода, т. е. с уменьшением абсолютных размеров объектов. При решении задач геомеханики методами обычно испытывают серию моделей. Например, сначала на моделях мелкого масштаба изучают общие закономерности процессов геомеханики в пределах всего участка массива, подверженного влиянию выработки, а затем на моделях крупного масштаба с большей детальностью изучают закономерности процессов в более локальной области массива, например, процессов взаимодействия пород кровли с крепью очистной выработки. При этом обычно в модели крупного масштаба воспроизводят лишь некоторую часть массива, а действие веса остальной части массива до поверхности компенсируют с помощью пригрузки, осуществляемой нагрузочными приспособлениями различного типа. 7.2. Основные положения подобия В основе методов моделирования лежит учение о подобии, основы которого заложены еще И. Ньютоном (1643-1721 гг.). Подобие – это взаимно-однозначное соответствие между двумя объектами, при котором функции перехода от параметров, характеризующих один из объектов, к соответствующим параметрам другого известны, а математические описания этих объектов могут быть преобразованы в тождественные. Необходимым и достаточным признаком подобия является равенство однотипных критериев подобия. Критериями подобия называют безразмерные числа, составленные из размерных физических параметров, определяющих рассматриваемые физические явления. Основные свойства подобных явлений и признаки подобия характеризуются тремя теоремами подобия. Первая теорема – подобными называются явления, происходящие в геометрически подобных системах, если у них во всех сходственных точках отношения одноименных величин есть постоянные числа (формулировка М. В. Кирпичева). Вторая теорема устанавливает возможность такого преобразования физического уравнения связи, описывающего данное явление, при котором получают уравнение, составленное из критериев подобия. Согласно третьей теореме подобия, необходимым и достаточным условием подобия двух объектов является одинаковые определяющие критерии подобия и подобные условия однозначности. При характеристике механических процессов механическое подобие определяется масштабом линейных размеров (геометрическое подобие), масштабом перемещения в пространстве (кинематическое подобие) и масштабом действующих сил (динамическое подобие). Условие геометрического подобия состоит в том, что все размеры пространства, занятого системой в модели, а также размеры отдельных элементов модели изменены в определенное число сравнению с соответствующими элементами натурной системы: 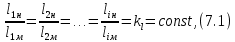 где 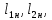 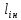 – линейные размеры натурного объекта (индекс н относится – линейные размеры натурного объекта (индекс н относится к параметрам объекта в натуре); 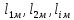 – линейные размеры в модели (индекс м относится к параметрам в модели), – линейные размеры в модели (индекс м относится к параметрам в модели), 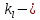 коэффициент соотношения (масштаб) линейных параметров. коэффициент соотношения (масштаб) линейных параметров. Соотношение площадей объекта в натуре 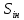 и площади в модели и площади в модели 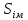 составит составит 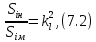 а для объемов в натурном объекте 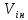 и в модели и в модели 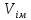 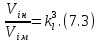 Кинематическое подобие системы определяется тождественностью направления и пропорциональностью величин времени, действующих скоростей и ускорений: 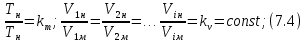 где 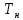 (м) – время; (м) – время; 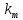 – масштаб времени; – масштаб времени; 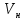 (м) – скорость системы; (м) – скорость системы; 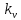 – масштаб скорости. – масштаб скорости. Динамическое подобие системы заключается в тождественности направления действия сил и напряжений и пропорциональности их значений: 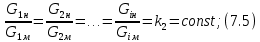 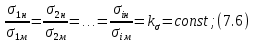 где 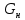 (м) – сила в системе, (м) – сила в системе, 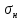 (м) – напряжения в системе; (м) – напряжения в системе; 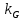 – масштаб сил; – масштаб сил; 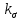 – масштаб напряжений. – масштаб напряжений. Преобразуем соотношение сил, выразив их значение через массу, ускорение, плотность, объем: 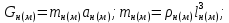 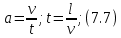 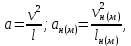 где 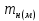 – масса системы, – масса системы, 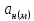 – ускорение системы, – ускорение системы, 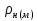 – плотность системы, – плотность системы,  тогда 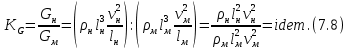 Это выражение является общим законом подобия Ньютона, а получаемое безразмерно число – числом, критерием Ньютона 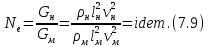 Для напряжений 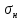 (м) = (м) = 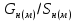 в условиях действия гравитационных сил в условиях действия гравитационных сил 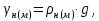 где 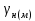 – объемный вес системы, – объемный вес системы, 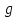 = 9,81 м/с2– ускорение силы тяжести, = 9,81 м/с2– ускорение силы тяжести, тогда 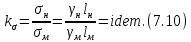 Очень важно отметить, что для выявления критериев подобия при моделировании необходимо составление уравнения объекта (явления, процесса), для этого – выявление соотношения сил в процессе. 7.3. Методы моделирования Проанализируем возможности моделирования процессов механики горных пород по критерию динамического подобия: 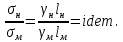 При геометрическом масштабе моделирования, равном100: 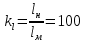 Если сохранить в модели и в натурном объекте равенство напряжений, тогда 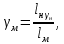 а для условий примера а для условий примера 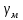 = 100 = 100 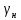 , т. е. объемный вес материала модели должен в 100 раз превышать объемный вес горных пород. Это условие можно выполнить, применив в модели натуральные горные породы и придав им фиктивный объемный вес с помощью инерционных сил. Инерционные силы можно создать путем вращения модели в центрифуге. Этот метод предложен в 1932 году профессором Г. И. Покровским и Н. Н. Давиденковым и носит название «метод центробежного моделирования». , т. е. объемный вес материала модели должен в 100 раз превышать объемный вес горных пород. Это условие можно выполнить, применив в модели натуральные горные породы и придав им фиктивный объемный вес с помощью инерционных сил. Инерционные силы можно создать путем вращения модели в центрифуге. Этот метод предложен в 1932 году профессором Г. И. Покровским и Н. Н. Давиденковым и носит название «метод центробежного моделирования». Если же отказаться от равенства напряжений в натурном объекте и в модели ( 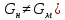 , то условием подобия будет выражение , то условием подобия будет выражение 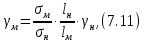 или для условий примера 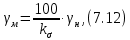 т. е. материал модели должен отличаться от материала натурного объекта. Искусственные материалы, соответствующие механические характеристики которых в принятом геометрическом масштабе моделирования удовлетворяют по отношению к моделируемым горным породам условию, называются материалами – эквивалентами данным горным породам, или эквивалентными материалами. Метод же моделирования называют методом эквивалентных материалов (разработанных профессором Г. Н. Кузнецова в 1936 г.). Метод центробежного моделирования Метод центробежного моделирования состоит в том, что модель из горных пород моделируемого объекта, выполненную в заданном геометрическом объеме, помещают в каретку центрифуги (рис. 7.1) и путем равномерного вращения нагружают объемными инерционными силами, придавая таким образом породам модели некоторый фиктивный объемный вес в соответствии с формулой (7.10). 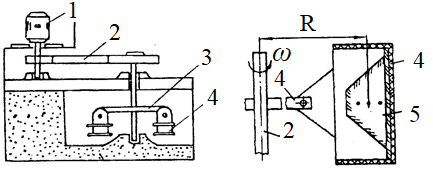 Рис. 7.1. Схема большой центрифуги института ВОДГЕО: 1 – двигатель; 2 – ременная передача; 3 – коромысло; 4 – каретки; 5 – модель Фиксируя деформации и напряжения пород модели в различных точках, (таким путем) изучают закономерности механики горных пород для моделируемых условий, а также устанавливают оптимальные параметры горнотехнических объектов и сооружений по фактору устойчивости. Основным параметром центробежного моделирования считается масштаб модели, показывающей, во сколько раз во вращающейся модели увеличен объемный вес порода. По формуле (7.10) 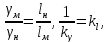 т. е. масштаб равен геометрическому масштабу модели. Зависимость между числом оборотов центрифуги и масштабом центробежного моделирования приближенно выражается формулой 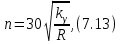 где 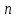 –число оборотов центрифуги в минуту; –число оборотов центрифуги в минуту; 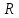 – радиус вращения модели, м. – радиус вращения модели, м. Современные центрифуги позволяют испытывать модели высотой до 0,4-0,5 м. Обычно применяемый масштаб моделирования от 20 до 500. Например, центрифуга Криворожского НИГРИ имеет следующие параметры: наружный диаметр 6 м, эффективный радиус 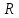 = 2,5 м, максимальная скорость вращения = 2,5 м, максимальная скорость вращения 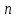 = 425 об/мин, максимальный масштаб центробежного моделирования = 425 об/мин, максимальный масштаб центробежного моделирования 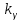 = 500, размеры кареток 1,5х0,8х0,6 м, мощность привода 650 кВт. = 500, размеры кареток 1,5х0,8х0,6 м, мощность привода 650 кВт. Важным достоинством центробежного моделирования является использование для изготовления модели натуральных горных пород, при этом соблюдается соответствие между размерами частиц и молекул (для некоторых задач это имеет большое значение). Вместе с тем метод центробежного моделирования имеет ряд ограничений; не обеспечивает однородность механического силового поля; ни выдерживается постоянство масштаба моделирования; небольшие размеры моделей. Метод эквивалентных материалов В отличие от метода центробежного моделирования в методе эквивалентных материалов взамен натуральных горных пород используют некоторые искусственные материалы, эквивалентные породам моделируемой толщи, механические характеристики которых в принятом масштабе моделирования удовлетворяют соотношению. Моделирование состоит из нескольких последовательных этапов. На первом этапе, сформулировав задачу, устанавливают возможную степень схематизации геологического разреза пород, подлежащего воспроизведению в модели, определяют начальные и граничные условия, возможность и степень их удовлетворения в модели. Исходя из этого устанавливают размеры участка толщи, подлежащего моделированию, и выбирают геометрический масштаб моделирования. На этом е этапе устанавливают, возможно ли сведение поставленной задачи к плоской и соответственно моделирование на плоской модели или требуется более сложное моделирование. Второй этап состоит в подборе эквивалентных материалов для воспроизведения моделируемой толщи пород. К настоящему времени разработаны рецептура и технология изготовления эквивалентных материалов с различными физическими свойствами. Подобрав и уточнив подходящие эквивалентные материалы для моделируемой толщи, приступают к следующему этапу – изготовлению самой модели. Модели изготовляют на испытательных стендах, представляющих собой жесткие рамные металлические конструкции. В зависимости от решаемых задач моделирование ведут в различных геометрических масштабах: мелких – от 1:400 до 1:100 или крупных – от 1:60 до 1:10. Толщи слабых пород моделируют только в крупных масштабах. Разделение толщи пород в модели на отдельные слои обеспечивают путем присыпки поверхности каждого слоя крупной молотой слюдой, трещиноватость или кливаж воспроизводят насечкой только что изготовленных слоев до отвердения или схватывания материалов. При изготовлении плоских моделей толщи слабых пород вместо опалубки используют прозрачные ограждение стенки, стационарно закрепляемые на весь период испытания модели. В процессе изготовления модели в намеченных слоях устанавливают марки и датчики для регистрации картины поля напряжений, деформаций и смещений в период испытания, а также встраивают в модели приборы, воспроизводящие работу крепи. Для определения напряженного состояния и его изменений при испытании моделей применяют микродинамометры различных конструкций. Напряженное состояние и деформации элементов модели можно определять также с помощью спаренных микроскопов, жестко соединенных между собой и позволяющих определять с высокой точностью смещения двух точек относительно друг друга. Для определения сдвижений точек плоской модели в процессе ее испытания применяют метод фотофиксации – периодическое фотографирование боковой поверхности модели с установленными в ней марками и последующие измерения смещений марок на фотоснимках, осуществляемые на компараторе. Метод фотофиксации позволяет быстро и притом одновременно регистрировать смещения всех точек на боковой поверхности модели. База измерений в моделях всеми упомянутыми способами составляет 40-50 мм, а относительная погрешность (1-2) 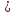 10-4, т. е. на порядок ниже, чем при измерениях в натуре. 10-4, т. е. на порядок ниже, чем при измерениях в натуре. В объемных моделях для измерения сдвижений точек массива применяют миниатюрные скважины с глубинными реперами, в принципе подобные скважинам в натурных условиях. Для регистрации смещений с разрывом сплошности и участков появления трещин после испытания моделей осуществляют их послойное вскрытие. Для воспроизведения работы крепей применяют приборы пьезометрического и рычажного типов для моделей мелких масштабов или рычажно-маятникового и гидравлического – для моделей крупных масштабов. Завершающим этапом моделирования является собственно испытание модели, т. е. воспроизведение в определенном масштабе времени процесса перемещения забоя выработки и регистрации изменений полей напряжений, деформаций и смещений при разработке. По окончании испытания модели обычно из ее части, не подвергнутой при испытаниях деформациями, вырезают образцы материалов-эквивалентов и проводят контрольные определения их свойств. Метод эквивалентных материалов позволяет с большой степенью детальности проследить процессы деформирования в толще пород при движении забоя выработки, особенно с разрывом сплошности, что обычно исключено при других методах моделирования. Вследствие этого метод эквивалентных материалов является весьма эффективным, благодаря чему он получил широкое применение при решении различных задач геомеханики. Поляризационно-оптический метод моделирования Поляризационно-оптический или просто оптический метод моделирования является примером аналогового моделирования. Оптический метод моделирования позволяет устанавливать распределение и значения напряжений в массивах пород и элементах сооружений любой конфигурации, когда деформации модели происходят без разрыва сплошности. Метод основан на свойстве большинства прозрачных изотропных материалов, называемых оптически чувствительными, при приложении механических нагрузок приобретать оптическую анизотропию и проявлять способность двойного лучепреломления. Последнее заключается в том, что луч света, проходя через напряженную прозрачную кристаллическую среду, разлагается на две взаимно перпендикулярные плоскополяризованные составляющие, распространяющиеся внутри среды с различной скоростью. В частности, для задач геомеханики весьма удобно применение органических стекол и эпоксидных смол. При этом в пластинках из указанных материалов в заданном масштабе вырезают контуры изучаемых выработок (или систем выработок), вокруг которых исследуют распределение напряжений при различных схемах нагружения пластинок по контуру растягивающими или сжимающими Силами. Величины и направления главных напряжений определяют при просвечивании плоской модели в полярископе. Поляризованный свет можно получить из естественного с помощью поляризаторов – анизотропных кристаллов, пропускающих свет только в одном направлении (исландский шпат, кварц, турмалин). Метод оптического моделирования позволяет получить весьма наглядное представление о поле напряжений в массиве пород вокруг выработок любой конфигурации. Поэтому даже получение только качественной картины распределения напряжений дает возможность сделать подчас важные заключения и выводы, выделить наиболее и наименее напряженные участки, наметить пути достижения оптимального распределения напряжений. Для решения задач, связанных с динамическими процессами в породных массивах, в настоящее время часто применяют электро-аналоговые методы моделирования, т. е. методы электрического моделирования механических полей. Электрические модели могут быть двух типов. В одном из них – методе электродинамических аналогий (ЭГДА), предложенном в 1922 г. акад. Н. Н. Павловским, используют меняющиеся электрические свойства сплошной проводящей среды. Другой, известный под названием метода электрических сеток прямой аналогии (ЭСПА), предусматривает замену сплошной среды сеткой из некоторых элементарных электрических ячеек, параметры которых назначают, исходя из свойств среды в механической системе и критериев подобия. Электрические ячейки – элементы напряжения, силы тока, индуктивности, емкости – служат аналогами механического напряжения, скорости упругого смещения, массы, податливости элементарных объемов моделируемого массива пород. |
