Статистика. Курс лекций по теории статистики

• Название: Курс лекций по теории статистики
• Анкор: Статистика
• Дата: 31.01.2022
• Размер: 3.05 Mb.
• Имя файла: Teoria_statistikiLektsii.doc
• Тип: Курс лекций; #347192
• страница: 22 из 37

9.2.Парная регрессия на основе метода наименьших квадратов и метода группировок

Парная регрессия характеризует связь между двумя признаками: результативным и факторным. Аналитически связь между ними описывается уравнениями:

прямой

гиперболы (8.3)

параболы

и так далее.

Определить тип уравнения можно, исследуя зависимость графически, однако существуют более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, то это свидетельствует о том, что связь между ними линейная, а при обратной связи - гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная регрессия.

Оценка параметров уравнений регрессии (a₀, a₁, и a₂ - в уравнении параболы второго порядка) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели (a₀ , a₁), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:



Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид: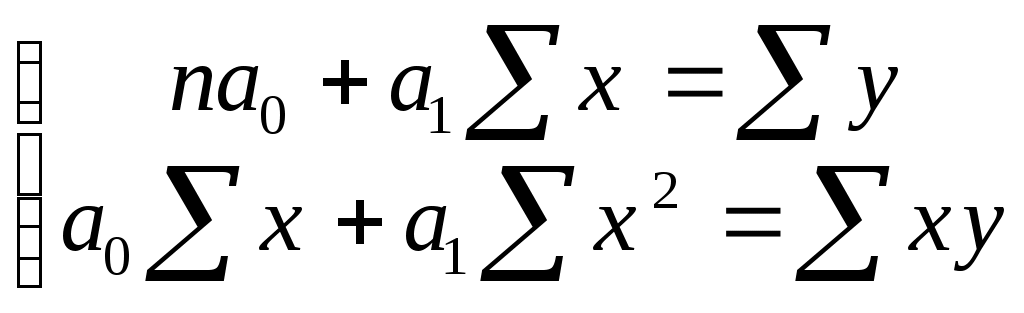

(8.4)

где n - объем исследуемой совокупности (число единиц наблюдения).

В уравнениях регрессии параметр a₀ показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков; коэффициент регрессии a₁ показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.

Например, имеются данные, характеризующие деловую активность закрытого акционерного общества (ЗАО): прибыль (млн. руб.) и затраты на 1 руб. произведенной продукции.

Таблица 8.2

Зависимость между прибылью ЗАО

и затратами на 1 руб. произведенной продукции

№ п/п	Прибыль (млн. руб.) (y)	Затраты на 1 руб. произведенной продукции (коп.) (x)	x2	xy
1	221	96	9216	21216	193
2	1070	77	5929	82390	1044
3	1001	77	5929	77077	1044
4	606	89	7921	53934	507
5	779	82	6724	63878	813
6	789	81	6561	63909	865
Итого	4466	502	42280	362404	4466

Предположим наличие линейной зависимости между рассматриваемыми признаками.
Система нормальных уравнений для данного примера имеет вид: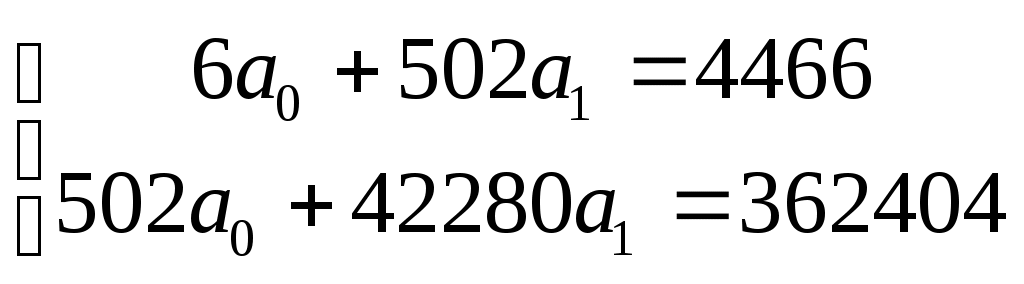


Отсюда: a₀ = 4494,06; a₁ = -44,8
Следовательно, =4494,06-44,8x.
На практике исследования часто проводятся по большому числу наблюдений. В этом случае исходные данные удобнее представлять в сводной групповой таблице. При этом анализу подвергаются сгруппированные данные и по факторному (x) и по результативному (y) признакам, то есть уравнения парной регрессии целесообразно строить на основе сгруппированных данных.
Если значения x и y заданы в определенных интервалах (a, b), то для каждого интервала сначала необходимо определить середину (x’/y’ = (a+b)/2), а затем уже коррелировать значения x’ и y’ и строить уравнения регрессии между ними.

Например, определим зависимость между величиной уставного капитала и числом занятых на предприятиях, выставивших акции на чековые аукционы в 1996 г. в одном из регионов, который характеризуется следующими данными:

Таблица 8.3

Распределение предприятий, выставивших акции

на чековые аукционы в 1996 г., по величине уставного капитала

и числу занятых в одном из регионов

Уставной капитал (млн.руб.) (у)	Число занятых (чел.) (х)					Число предприятий, fy	yfy	xyfy
		14-70	70-126	126-182	182-238
	xi yi	42	98	154	210
745-2684 2684-4624 4624-6564 6564-8503 8503-125842	1714,5 3654,0 5594,0 7533,5 67172,5	4 1 - 1 2	6 3 1 1 -	2 - 1 2 1	3 - - - 2	15 4 2 4 5	2517,5 14616,0 11188,0 30134,0 335862,5	2904363 1227744 1409688 3374995 44199505
Число предприятий, fx	-	8	11	6	5	30	417518,0	53533813
xfx	-	336	1078	924	1050	3388
x2fx		14112	105644	142296	220500	482552

Предположим наличие линейной зависимости между рассматриваемыми признаками.

Система нормальных уравнений для определения коэффициентов уравнения регрессии примет вид: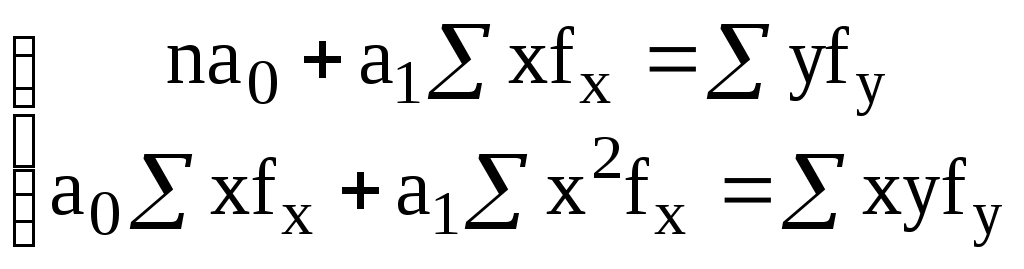



где n=30 - число анализируемых предприятий;
f_x/f_y- число предприятий, согласно распределению, соответственно по факторному и результативному признакам;
yf_y / xf_x- значения результативного и факторного признака по конкретной группе предприятий.
Так для первой группы:

yf_y=1714,515=25717,5; xf_x=428=336

xyf_y=1714,5442+1714,5698+1714,52154+1714,53210= =2904363

x²f_х=42428=14112

Таким образом, подставив в систему суммарные значения, получим:



a₀=6640; a₁=64

Отсюда =6640+64x.