Статистика. Курс лекций по теории статистики

• Название: Курс лекций по теории статистики
• Анкор: Статистика
• Дата: 31.01.2022
• Размер: 3.05 Mb.
• Имя файла: Teoria_statistikiLektsii.doc
• Тип: Курс лекций; #347192
• страница: 24 из 37

9.4. Собственно-корреляционные параметрические методы изучения связи.

Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного (при изучении парных зависимостей) или нескольких (множественных) факторных.
Линейный коэффициент корреляции характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.

В теории разработаны и на практике применяются различные модификации формулы расчета данного коэффициента:
(8.5)
Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле: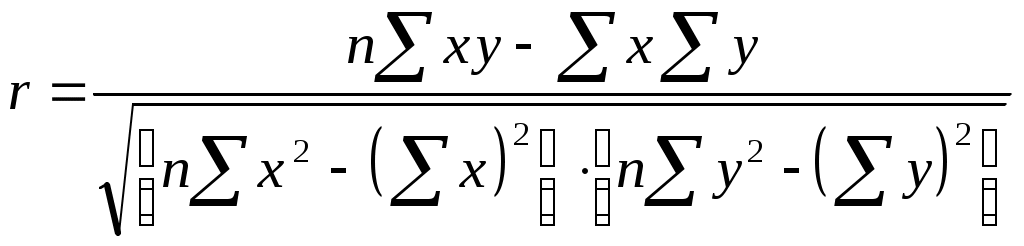
(8.6)
Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:

(8.7)

где - коэффициент регрессии в уравнении связи;

- среднеквадратическое отклонение соответствующего, статистически существенного, факторного признака.
Линейный коэффициент корреляции изменяется в пределах от -1 до 1: . Знаки коэффициентов регрессии и корреляции совпадают. При этом интерпретацию выходных значений коэффициента корреляции можно представить в следующей таблице:

Таблица 8.5

Оценка линейного коэффициента корреляции

Значение линейного коэффициента связи	Характер связи	Интерпретация связи
r = 0	отсутствует	-
0	прямая	с увеличением x увеличивается y
-1<r<0	обратная	с увеличением x уменьшается y и наоборот
r=1	функциональная	каждому значению факторного признака строго соответствует одно значение результативного признака

Пример: На основе выборочных данных о деловой активности однотипных коммерческих структур оценить тесноту связи между прибылью у (млн. руб.) и затратами на 1 руб. произведенной продукции x (коп.).
Таблица 8.6

Расчетная таблица для определения коэффициента корреляции

№ п/п	y	x	yx	y2	x2
1	221	96	21216	48841	9216
2	1070	77	82390	1144900	5929
3	1001	77	77077	1002000	5929
4	606	89	53934	367236	7921
5	779	82	63878	606841	6724
6	789	81	63909	622520	6561
Сумма	4466	502	362404	3792338	42280
Средняя	744,33	83,67	60400,67	632056,33	7046,67

1. Используя формулу (8.5) получаем:






2. По формуле (8.6) значение коэффициента корреляции составило:


Таким образом, результат по всем формулам одинаков и свидетельствует о сильной обратной зависимости между изучаемыми признаками.
В случае наличия линейной и нелинейной зависимости между двумя признаками для измерения тесноты связи применяют так называемое корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение.
Эмпирическое корреляционное отношение рассчитывается по данным группировки, когда характеризует отклонения групповых средних результативного показателя от общей средней:
(8.8)
где - корреляционное отношение;

- общая дисперсия;

- средняя из частных (групповых) дисперсий;

- межгрупповая дисперсия (дисперсия групповых средних).
Все эти дисперсии есть дисперсии результативного признака.

Теоретическое корреляционное отношение определяется по формуле: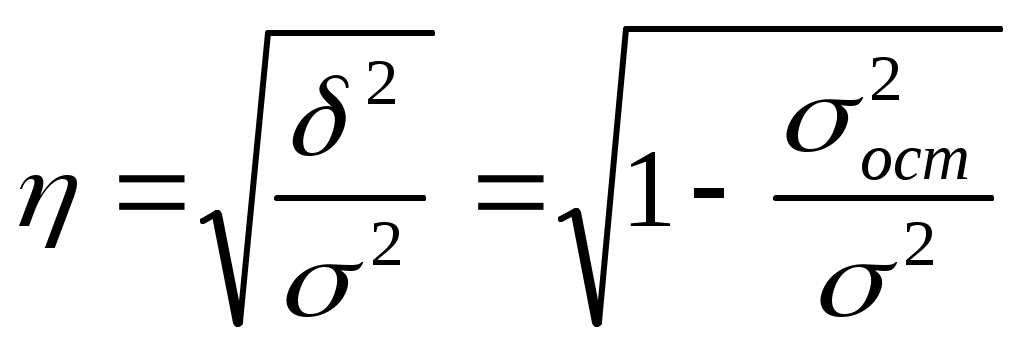

(8.9)

где - дисперсия выравненных значений результативного признака, то есть рассчитанных по уравнению регрессии;

- дисперсия эмпирических (фактических) значений результативного признака.

Корреляционное отношение изменяется в пределах от 0 до 1 и анализ степени тесноты связи полностью соответствует линейному коэффициенту корреляции (таблица 8.1).
Для измерения тесноты связи при множественной корреляционной зависимости, то есть при исследовании трех и более признаков одновременно, вычисляется множественный и частные коэффициенты корреляции.
Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков.

Множественный коэффициент корреляции для двух факторных признаков вычисляется по формуле: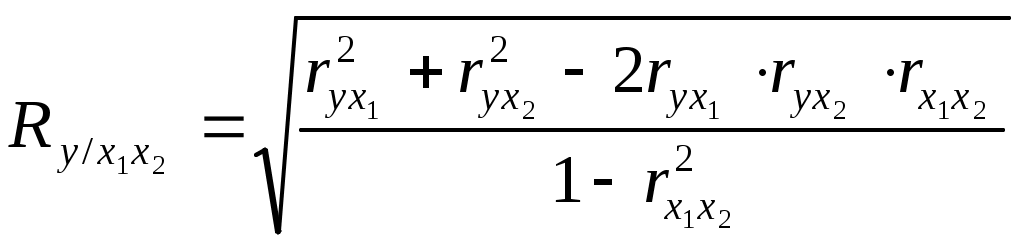
(8.10)
где - парные коэффициенты корреляции между признаками.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: .

Приближение к единице свидетельствует о сильной зависимости между признаками.

На основе данных таблицы 8.4 рассчитаем коэффициент множественной корреляции и его ошибку:
; ; .
Множественный коэффициент корреляции составит:

Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками и при фиксированном значении других факторных признаков, то есть когда влияние исключается, то есть оценивается связь между и в «чистом виде».
В случае зависимости 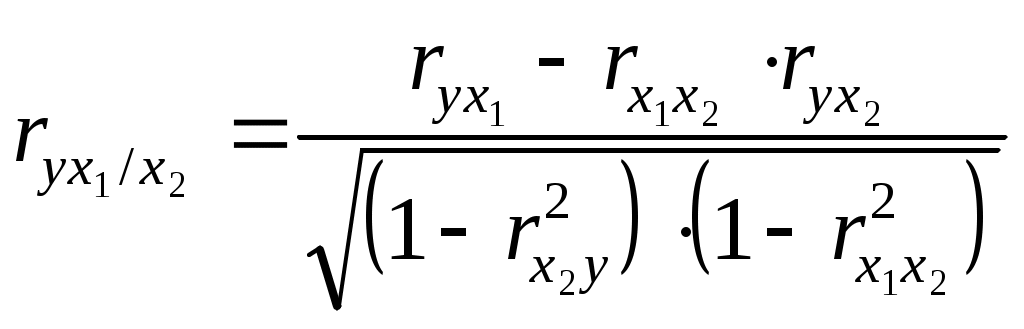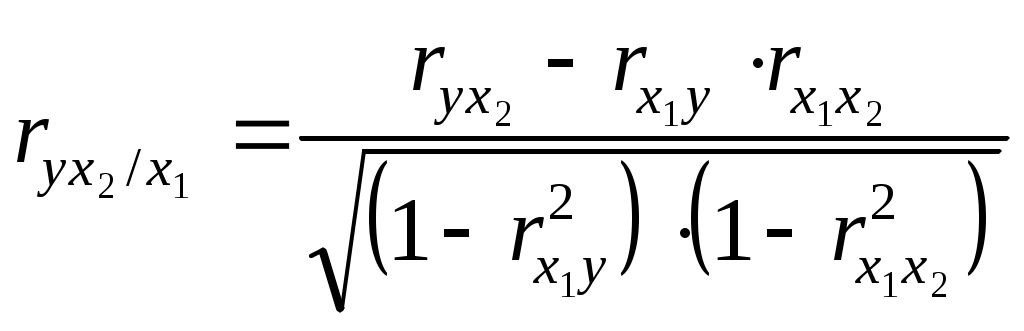от двух факторных признаков и коэффициенты частной корреляции имеют вид:


(8.11)
где - парные коэффициенты корреляции между указанными в индексе переменными.

В первом случае исключено влияние факторного признака , во втором - .

На основании приведенных выше данных о зависимости трех факторов деятельности предприятий вычислим частные коэффициенты корреляции (см. табл. 8.4):


; .