Статистика. Курс лекций по теории статистики

• Название: Курс лекций по теории статистики
• Анкор: Статистика
• Дата: 31.01.2022
• Размер: 3.05 Mb.
• Имя файла: Teoria_statistikiLektsii.doc
• Тип: Курс лекций; #347192
• страница: 26 из 37

9.6. Методы изучения связи качественных признаков

При наличии соотношения между вариацией качественных признаков говорят об их ассоциации, взаимосвязанности. Для оценки связи в этом случае используют ряд показателей.
Коэффициент ассоциации и контингенции. Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции.
Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, то есть состоящим из двух качественно отличных друг от друга значений признака (например, хороший, плохой).

Таблица 8.7

Таблица для вычисления коэффициентов ассоциации

и контингенции

a	b	a+b
c	d	c+d
a+c	b+d	a+b+c+d

Коэффициенты вычисляются по формулам:

ассоциации: (8.15)

контингенции: 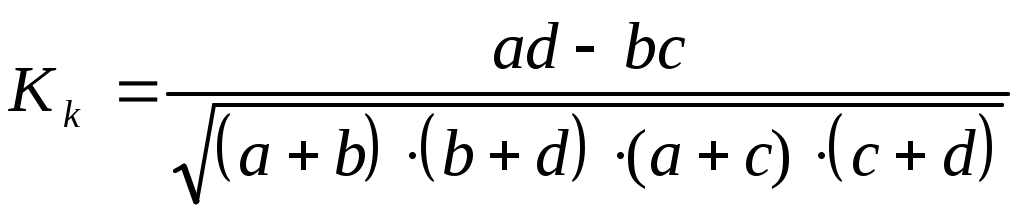(8.16)
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если или .
Пример. Исследуем связь между участием в забастовках рабочих и уровнем их образования. Результаты обследования характеризуются следующими данными:
Таблица 8.8

Зависимость участия рабочих в забастовках

от образовательного уровня

Группы рабочих	Число рабочих	Из них
		участвующих в забастовке	не участвующих в забастовке
Имеют среднее образование	100	78	22
Не имеют среднего образования	100	32	68
Итого	200	110	90

Таким образом, связь между участием в забастовках и их образовательным уровнем имеет место, но не столь существенна.
Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициента взаимной сопряженности Пирсона-Чупрова. Этот коэффициент вычисляется по следующей формуле: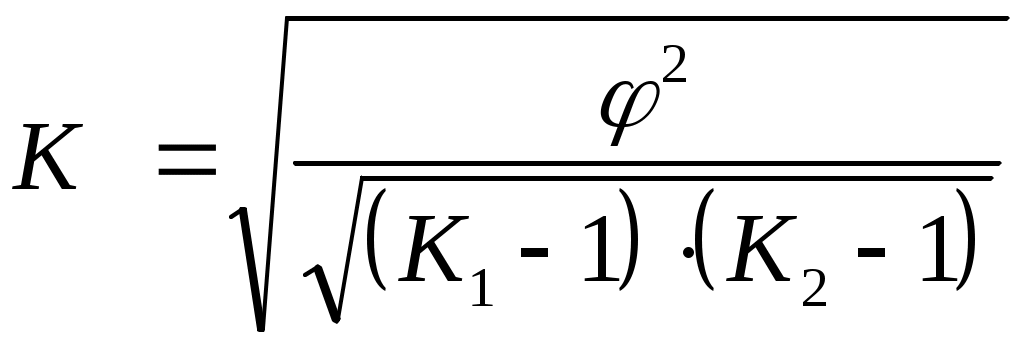

; (8.17)

где - показатель взаимной сопряженности;

- определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот, соответствующего столбца и строки. Вычитая из этой суммы «1», получим величину :

;

- число значений (групп) первого признака;

- число значений (групп) второго признака.

Чем ближе величина и K_ч к 1, тем теснее связь.
Таблица 8.9

Вспомогательная таблица для расчета коэффициента

взаимной сопряженности

у х	I	II	III	Всего
I
II
III
Итого

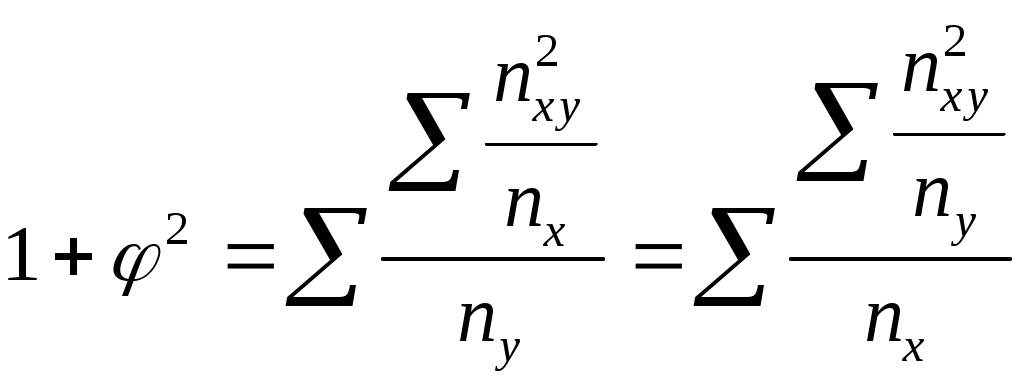Пример. С помощью коэффициента взаимной сопряженности исследуем связь между себестоимостью продукции и накладными расходами на реализацию.

Таблица 8.10

Зависимость между себестоимостью продукции и

накладными расходами на реализацию

Накладные расходы	Себестоимость			Итого
	Низкая	Средняя	Высокая
Низкие	19	12	9	40
Средние	7	18	15	40
Высокие	4	10	26	40
Итого	30	40	50	120

;

; K_ч= .

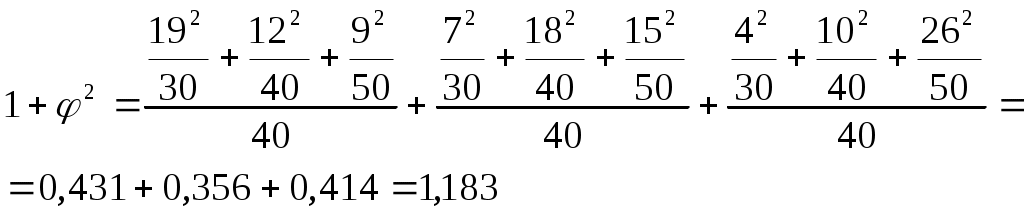Связь средняя.
Особое значение для оценки связи имеет биссериальный коэффициент корреляции, который дает возможность оценить связь между качественным альтернативным и качественным варьирующим признаками. Данный коэффициент вычисляется по формуле:

(8.18)

где и - средние в группах;

- среднее квадратическое отклонение фактических значений признака от среднего уровня;

- доля первой группы;

- доля второй группы;

- табулированные (табличные) значения -распределения в зависимости от .

Пример. Уровень дохода сотрудников одной коммерческой структуры характеризуется следующими данными:

Таблица 8.11

Зависимость уровня доходов сотрудников коммерческой

структуры от уровня их образования

	Уровень доходов, (руб.)
Уровень образования	200-300	300-400	400-500	500-600	Всего (чел.)
	250	350	450	550
Имеют высшее образование	5	7	6	4	22
Не имеют высшего образования	9	4	2	1	16
Итого	14	11	8	5	38

;
; ;


Величина биссериального коэффициента корреляции также подтверждает умеренную тесноту связи между изучаемыми признаками.