Курс лекцій НАРИСНА ГЕОМЕТРІЯ. Курс лекцій удк 514. 18 В.І. Лусь. Нарисна геометрія Курс лекцій. Харків хнамг, 2008. 127 с

• Название: Курс лекцій удк 514. 18 В.І. Лусь. Нарисна геометрія Курс лекцій. Харків хнамг, 2008. 127 с
• Анкор: Курс лекцій НАРИСНА ГЕОМЕТРІЯ.doc
• Дата: 09.05.2018
• Размер: 5.98 Mb.
• Имя файла: Курс лекцій НАРИСНА ГЕОМЕТРІЯ.doc
• Тип: Курс лекцій; #19052
• страница: 5 из 13

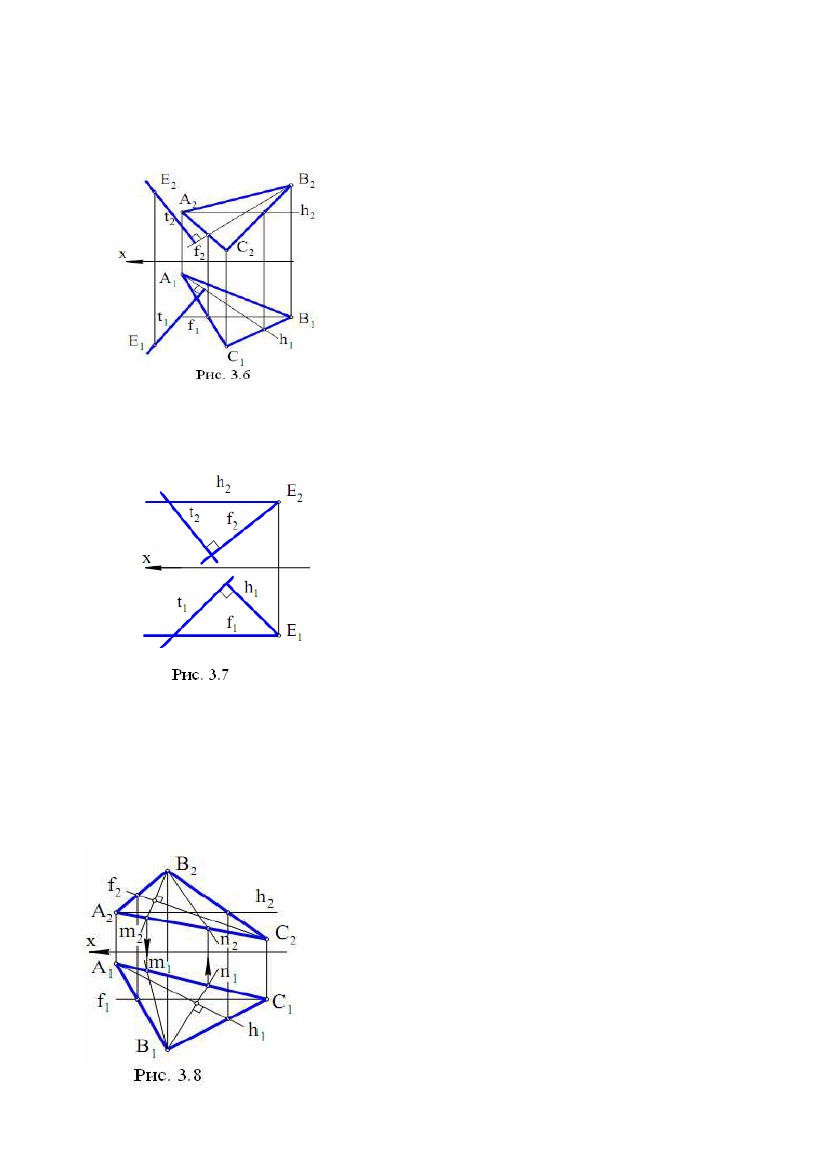h і f, а потім побудувати пряму t за умовами: t ⊥h, t ⊥f (рис. 3.5). У загальному

випадку прямі t і h, t і f - пари мимобіжних прямих.

Задача. Дано площину (∆АВС) і точку Е.Побудувати пряму t за∆

умовами: t ∋E, t ⊥(рис. 3.6).

Вирішення задачі може бути наступним:

1) будують лінії рівня h і f у площині Σ, де

h2║х, f1║x;

2) будують проекції t1 і t2 шуканої прямої t,

де t2 ∋Е2, t2 ⊥f2; t1 ∋E1, t1 ⊥h1.

У підсумку t1 , t2 – рішення задачі. Пряма t

мимобіжна з f і h.

Вибір ліній рівня h і f у якості пересічних

прямих у площині продиктований

наведеними вище умовами теореми про

проектування прямого кута й простотою побудов на КК(комплексному

кресленні). Якщо точка Е перебуває в площині , то послідовність побудов

залишається попередньою.

Задача. Дано пряму t і точку Е. Побудувати

площину, що проходить через точку Е і

перпендикулярну до прямої t (рис. 3.7).

Вирішення задачі ґрунтується на побудові

двох ліній рівня h(h1,h2) і f(f1,f2), що проходять

через точку Е: h2 ∋E2, h2║х, h1 ∋E1, h1 ⊥t1 ; f1

∋E1, f1 ║х, f2 ∋E2, f2 ⊥t2 .

Площина (h , f ) - рішення задачі

2.3. Лінії найбільшого нахилу

Приведемо відому в нарисній геометрії теорему: прямі в площині,

перпендикулярні до її ліній рівня, є лініями найбільшого нахилу цієї

площини до площин проекцій.

Ця теорема дозволяє виконувати побудови ліній

найбільшого нахилу на КК.

Задача. Дано площину Σ(∆АВС). Побудувати її

лінії найбільшого нахилу, щодо площин проекцій

П1 і П2 (рис. 3.8), що проходять через вершину В.

Алгоритм проекційного вирішення задачі буде

наступним:

1) будують в площині Σ лінії рівня h(h1,h2) і f(f1,f2),

де h2 ║ х, f1 ║ х;

2) будують спочатку m2 ∋B2, m2 ⊥f2, потім m1;

39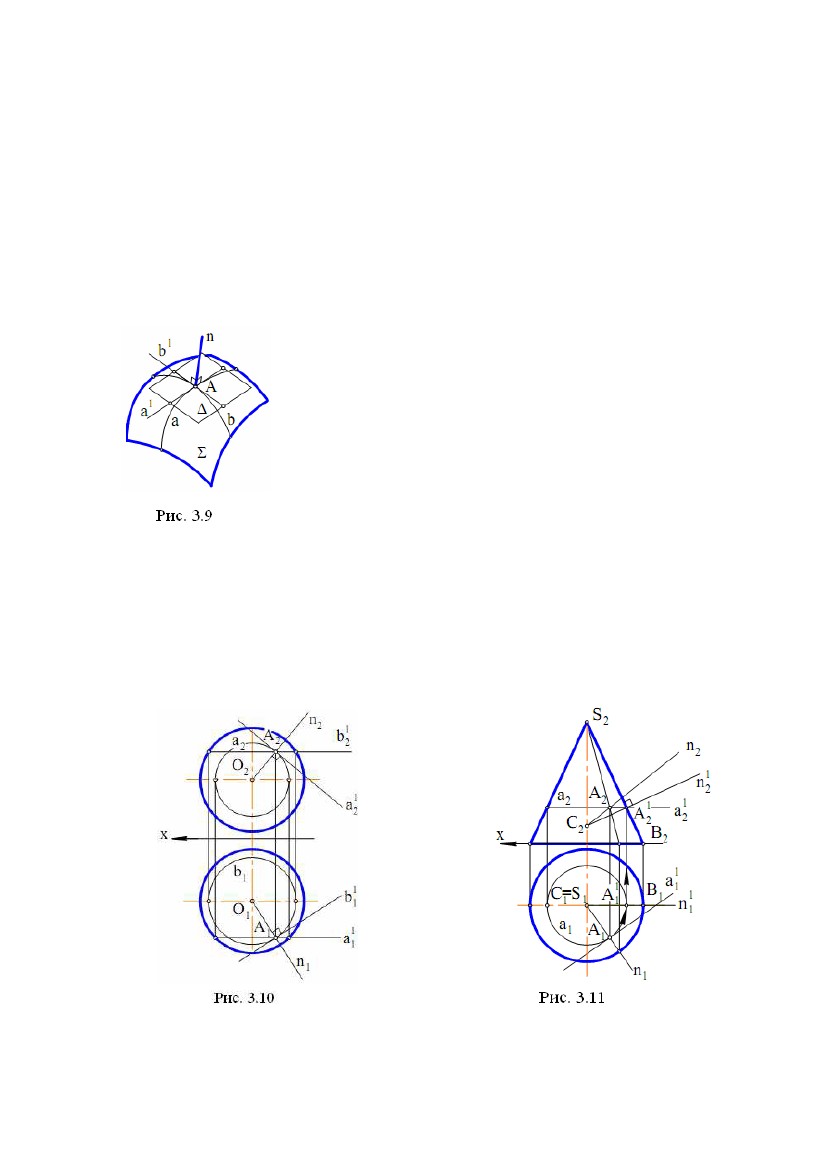

3) будують спочатку n1 ∋B1, n1 ⊥h1, потім n2.

Лінія m(m1,m2) визначає найбільший нахил площини Σ до площини проекцій

П2,а лінія n(n1,n2) визначає найбільший нахил площини Σ до площини проекцій

П1 .

2.4. Дотична площина й нормаль до поверхні

У будь-якій точці А поверхні можна побудувати єдину дотичну

площину (рис. 3.9). Для цього на поверхні через

точку А необхідно провести дві криві a і b, а потім

побудувати дві дотичні а1 і b1відповідно к a і b.

Дотична площина ∆ утворена прямими a1 і b1.

Пряма n ⊥∆називається нормаллю поверхні у

точці А.

Задача. Дано сферу і точку А на ній. Побудувати

дотичну площину і нормаль до сфери в точці А

(рис. 3.10).

Вирішення задачі можна виконати наступним

чином:

1) побудуємо два кола а(a1, a2) і b(b1 ,b2) на сфері, що перетинаються в

точці А(А1,А2);

2) проведемо дві дотичні а1(а11, а12) і b1(b11, b12 ) до кіл a і b відповідно; шукана

дотична площина утвориться дотичними a1 і b1;

3) побудуємо нормаль n(n1,n2) до поверхні сфери по наступних умовах: n1 ⊥b11

, n2 ⊥а12. Зазначимо, що поверхня сфери складається тільки із простих точок.

Задача. Дано конічну поверхню обертання і точку А на ній. Побудувати

дотичну площину і нормаль до поверхні в точці А (рис. 3.11).

Вирішення задачі:

40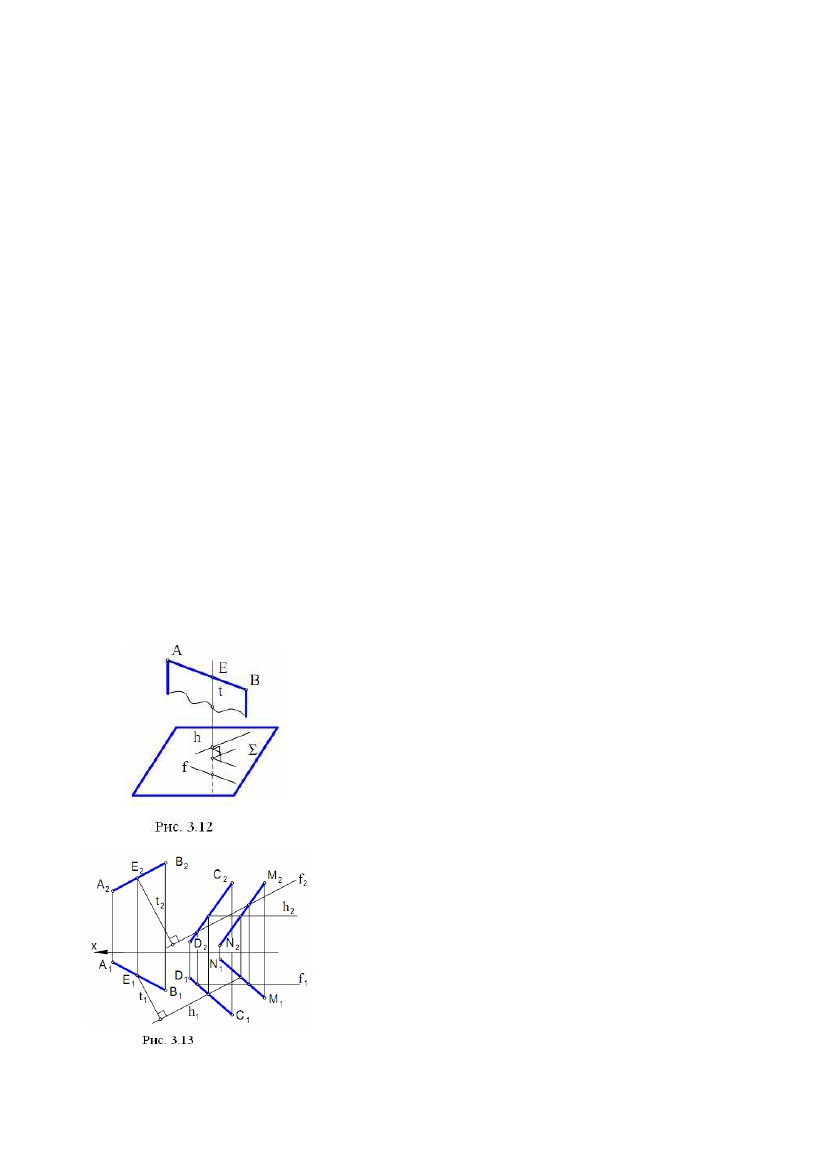

1) побудуємо на конічній поверхні дві лінії, що перетинаються в точці А:

коло а(a1, a2) і пряму b = SA(S1A1, S2A2);

2) проведемо дотичну а1(а11,а12 ) до кола а; дві пересічні в точці А прямі

a1 і SA утворять дотичну площину до поверхні конуса;

3) за допомогою перетворення обертанням (див. рис. 3.11) побудуємо

проміжне положення n1(n11,n12) шуканої нормалі n, а потім її шукане

положення n(n1,n2).

Вершина S - єдина особлива точка на поверхні конуса.

2.5. Перпендикулярність двох площин

Визначення. Дві площини називаються перпендикулярними, якщо кут

між ними дорівнює 90°. Приведемо без доказу теореми стереометрії, корисні

для вирішення наступних метричних задач:

1) Ознака перпендикулярності двох площин: якщо площина проходить

через перпендикуляр до іншої площини, то вона перпендикулярна до цієї

площини;

2) Якщо дві площини, перпендикулярні до третьої площини,

перетинаються, то пряма їхнього перетину перпендикулярна до третьої

площини;

3) Для похилої прямої, яка не є перпендикулярна до площини, має місце

твердження: через похилу проходить єдина площина, перпендикулярна до даної

площини.

Останнє твердження дозволяє запропонувати

наступний алгоритм побудови площини, що

проходить через похилу АВ і перпендикулярну

до заданої площини :

1) на АВ вибирають довільну точку Е;

2) будують пряму t таким чином, що t ∋Е; t ⊥h ;

t ⊥f , де h ⊂, f ⊂(рис. 3.12), тобто t ⊥.

Площина (АВ, t) буде єдиною площиною,

перпендикулярною до площини . Зазначимо,

що через пряму t ⊥проходить не одна

площина, перпендикулярна до .

Задача. Дано площину (CD, MN), де

CD║MN і пряму АВ (рис. 3.13). Побудувати на

КК площину, що проходить через АВ і

перпендикулярну до площини .

Алгоритм проекційного вирішення задачі:

1) будують лінії рівня h(h1,h2) і f(f1,f2) у площині

Σ, при цьому h2║х, f1║х;

41

2) будують проекції t1 і t2 прямої t таким чином, що t2 ∋E2 , t2 ⊥f2 ; t1 ∋E1,

t1 ⊥h1 , де Е ∈АВ – довільна точка.

Площина (АВ, t) - рішення задачі.

Задача. Дано площини (АВ, DC) і ∆(KL, PT), де AB ∩DC, KL║PT, а

також точку Е. Побудувати площину, що проходить через точку Е і

перпендикулярну до обох площин і ∆(рис. 5.17).

Одне з можливих рішень даної задачі полягає в наступному. Спочатку

будують лінію перетину заданих площин t = ∩∆. Потім, на підставі

наведених теорем стереометрії, будують площину, що проходить через точку Е

і перпендикулярна до лінії t. Будучи єдиною, ця площина являє собою рішення

задачі.

Можливий інший алгоритм вирішення даної задачі (див. рис. 5.16):

1) з даної точки Е опускають перпендикуляр а на площинуΣ;

2) із точки Е опускають перпендикуляр b на площину ∆.

Площина (a, b), де a ∩b = E, є рішенням задачі. Розглянемо реалізацію

цього алгоритму на КК (див. рис. 5.17).

1) У площині Σ побудуємо лінії рівня h1(h11, h12) і f1(f11, f12). При цьому

h12║x; f11║x.

2) У площині ∆ побудуємо лінії рівня h2(h21, h22) і f 2(f21, f22). При цьому

h22║х; f21║х.

3) Із точки Е опускаємо два перпендикуляри: а ⊥Σ, b ⊥∆. При цьому

1а2 ⊥f 2 , а1 ⊥h11 ; b2 ⊥f22 , b1 ⊥h21.

Дві прямі а і b, що перетинаються в точці Е, визначають шукану

площину, тобто площину, перпендикулярну до заданих площин і ∆.

42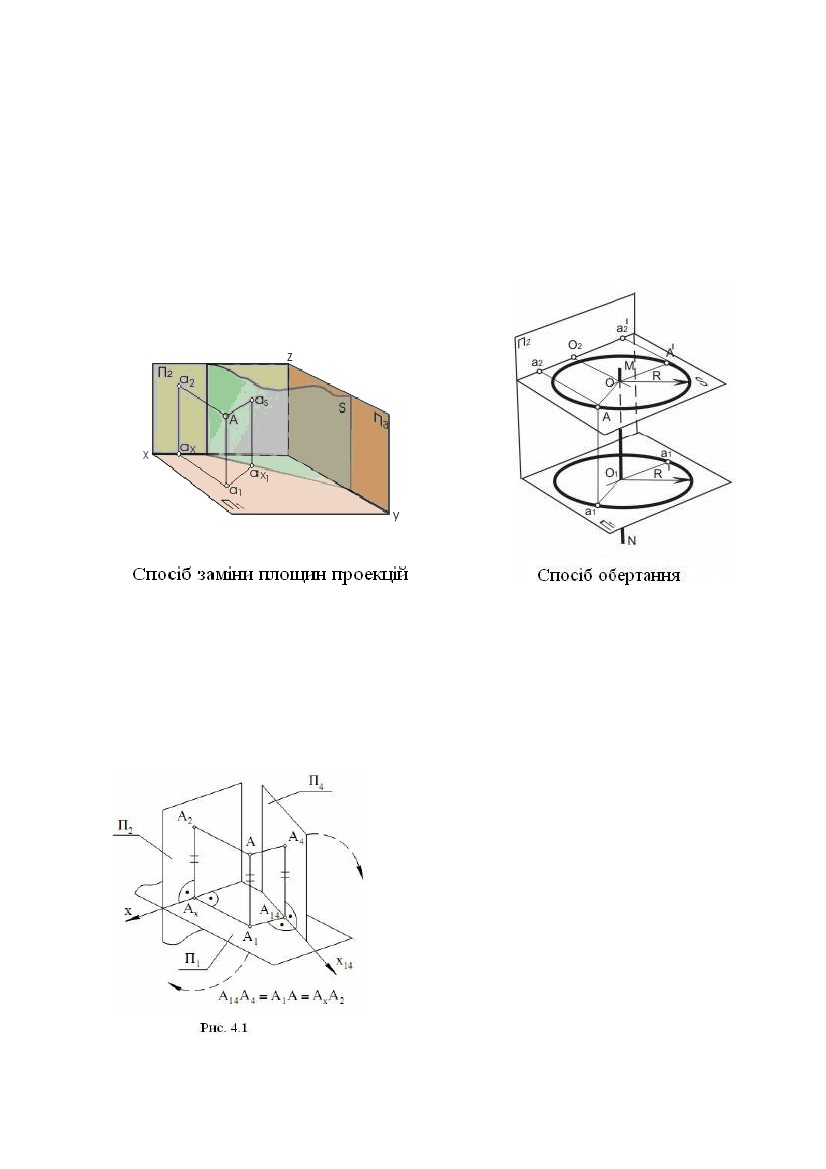

ЛЕКЦІЯ № 4. ПЕРЕТВОРЕННЯ КОМПЛЕКСНОГО КРЕСЛЕННЯ

Нарисна геометрія має у своєму розпорядженні способи, за допомогою

яких можна перейти від загальних положень заданих геометричних образів до

окремих, що значно спрощує вирішення задачі й дозволяє одержати більш

точну відповідь. Ці способи називаються способами перетворення проекцій і

полягають у послідовній заміні площин проекцій і в обертанні геометричних

образів навколо певних осей.

1. СПОСІБ ЗАМІНИ ПЛОЩИН ПРОЕКЦІЙ

Метод заміни площин проекцій полягає в тому, що замість однієї із

площин проекцій вводиться нова площина, перпендикулярна до іншої площини

проекцій.

На рис. 4.1 показана просторова схема

одержання комплексного креслення

точки А в системі (П1П2). точки А1 і А2 –

горизонтальна і фронтальна проекції

точки А, АА1АxА2 – прямокутник,

площина якого перпендикулярна до осі

X (рис. 4.1).

Нова площина П4 перпендикулярна до

П1. При проектуванні точки А на П4

одержимо нову проекцію А4, фігура

АА1А14А4 – прямокутник, площина якого

перпендикулярна до нової осі

x14 = П4 ∩ П1. Для одержання

комплексного креслення будемо

43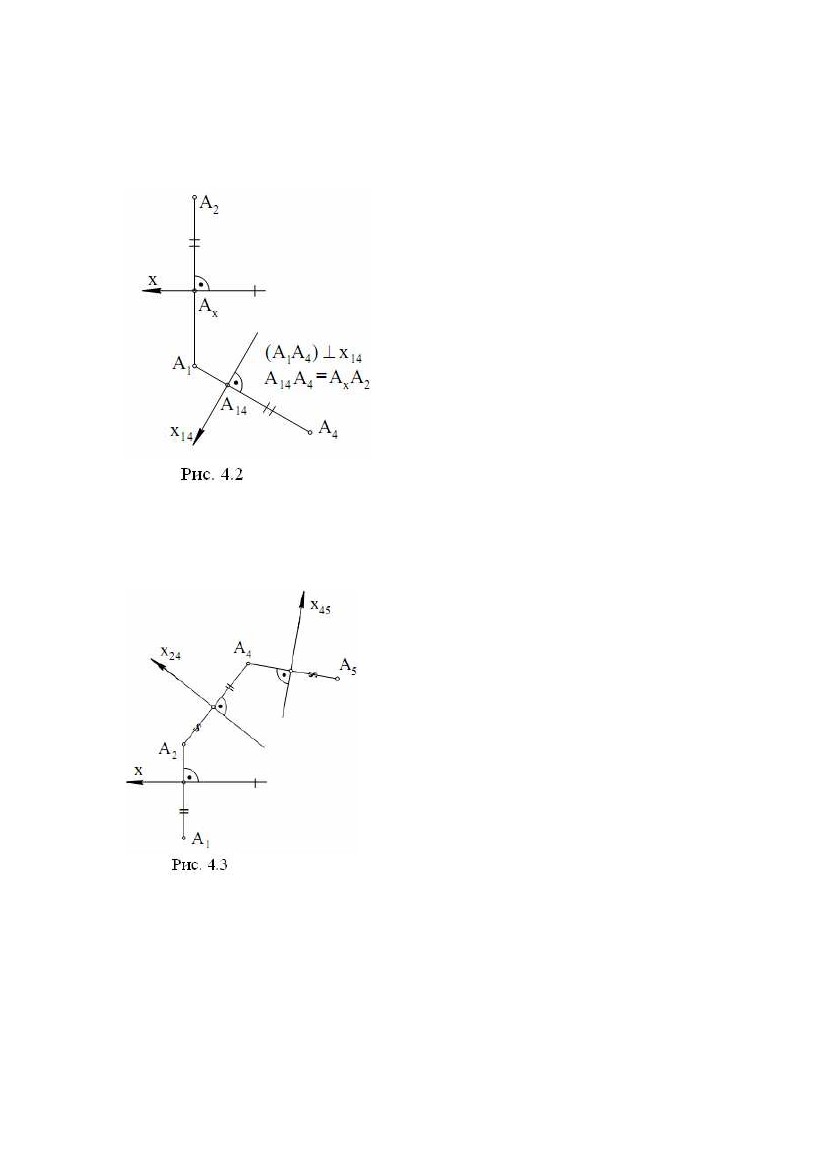

розглядати фігури, розташовані в площинах проекцій. Поворотом навколо осі

x14 сполучимо П4 з П1, потім поворотом навколо осі x сполучимо П1 (і П4) з П2

(на рис. 4.1 напрямки руху площин П4 і П1 показані штриховими лініями зі

стрілками).

Отримане креслення наведено на

рис. 4.2. Прямі кути на рис. 4.1, 4.2

позначені дугою з точкою, рівні

відрізки позначені двома штрихами

(протилежні сторони прямокутників на

рис. 4.1). Від комплексного креслення

точки А в системі (П1П2) перейшли до

комплексного креслення точки А в

системі (П1П4), замінили площину П2

на площину П4, замінили А2 на А4. На

основі цих побудов сформулюємо

правило заміни площин проекцій

(правило одержання нової проекції).

Через незамінну проекцію проводимо

нову лінію проекційного зв'язку

перпендикулярно до нової осі, потім від нової осі по лінії проекційного зв'язку

відкладаємо відрізок, довжина якого дорівнює відстані від замінної проекції до

старої осі, отримана при цьому точка і є нова проекція.

Напрямок нової осі будемо брати

довільно. Новий початок координат

вказувати не будемо.

На рис. 4.3 показаний перехід від

комплексного креслення в системі (П1П2)

до комплексного креслення в системі

(П2П4), а потім ще один перехід до

комплексного креслення в системі (П4П5).

Замість площини П1 введена площина П4,

перпендикулярна до П2, потім замість П2

введена площина П5, перпендикулярна до

П4. Використовуючи правило заміни

площин проекцій, можна виконати будь-

яку кількість замін площин проекцій.

1.1. Визначення відстані між двома точками

Відстанню між двома точками називається довжина відрізка, що з'єднує

ці точки. Для визначення відстані між двома точками А і В необхідно з'єднати

їх відрізком АВ (рис. 4.4), потім визначити довжину цього відрізка. Відрізок

загального положення не паралельний до жодної з площин проекцій.

44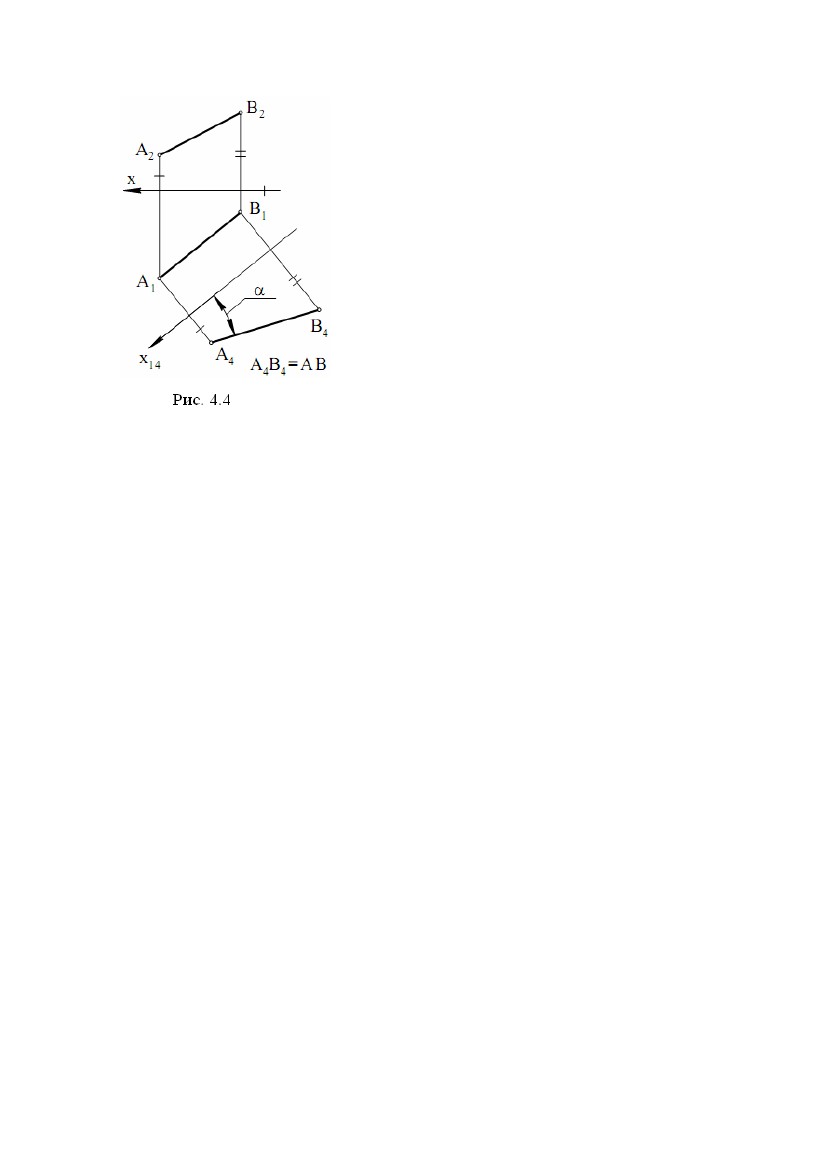

Довжини проекцій А1В1 і А2В2 менше

довжини відрізка АВ. Для того щоб

визначитидовжинувідрізкаАВ,

необхідно спроектувати його в натуральну

величину і виміряти цю проекцію, тому

що вона дорівнює відрізку АВ.

Введемо нову площину проекцій П4

паралельновідрізкуАВі

перпендикулярно до П1. При цьому нова

вісь x14 буде паралельна А1В1 (у

протилежному виразі пряма АВ і площина

П4 перетнуться). Кут нахилу відрізка АВ

до площини П4 дорівнює нулю, і АВ на П4

проектується в натуральну величину,

тобто А4В4 = АВ. Вимірявши відрізок

А4В4, одержимо довжину відрізка АВ.

Кожну з точок А4 і В4 будували з використанням правила заміни площин

проекцій.

Відстань між А1В1 і x14 не впливає на величину А4В4, тому може бути

взята довільно. У результаті введення П4 виконаний перехід від системи

(П1⊥П2) до системи (П1⊥П4), в якій пряма АВ, що проходить через відрізок АВ,

є лінією рівня.

На площині П4 (рис. 4.4) крім А4В4 = АВ одержали кут α, що дорівнює

куту між АВ і площиною П1, тому що площина цього кута паралельна до

площини П4. Якщо ввести нову площину П5 паралельно АВ і перпендикулярно

до П2, то нова вісь x25 буде паралельна А2В2. Одержимо А5В5 = АВ і кут β, що

дорівнює куту між АВ і площиною П2, тому що площина цього кута паралельна

площині П5.

1.2. Проектування прямої загального положення в точку на нову

площину проекцій

Надання фігурам окремого положення щодо площин проекцій значно

полегшує вирішення багатьох задач. Щоб пряма загального положення в новій

системі площин проекцій стала проектуючою прямою, необхідно, щоб нова

площина проекцій була перпендикулярна до прямої. Пряма на цю площину

спроектується в точку. Площина, перпендикулярна до прямої загального

положення, є площиною загального положення. Введення такої площини, як

нова площина проекцій неможливо, тому що нова площина проекцій повинна

бути перпендикулярна до однієї із «старих» площин проекцій. Таким чином,

вирішити задачу проектування прямої загального положення в точку однією

заміною площини проекцій не можна. Тому спробуємо вирішити задачу

спочатку для прямої окремого положення, а саме - для прямої рівня.

45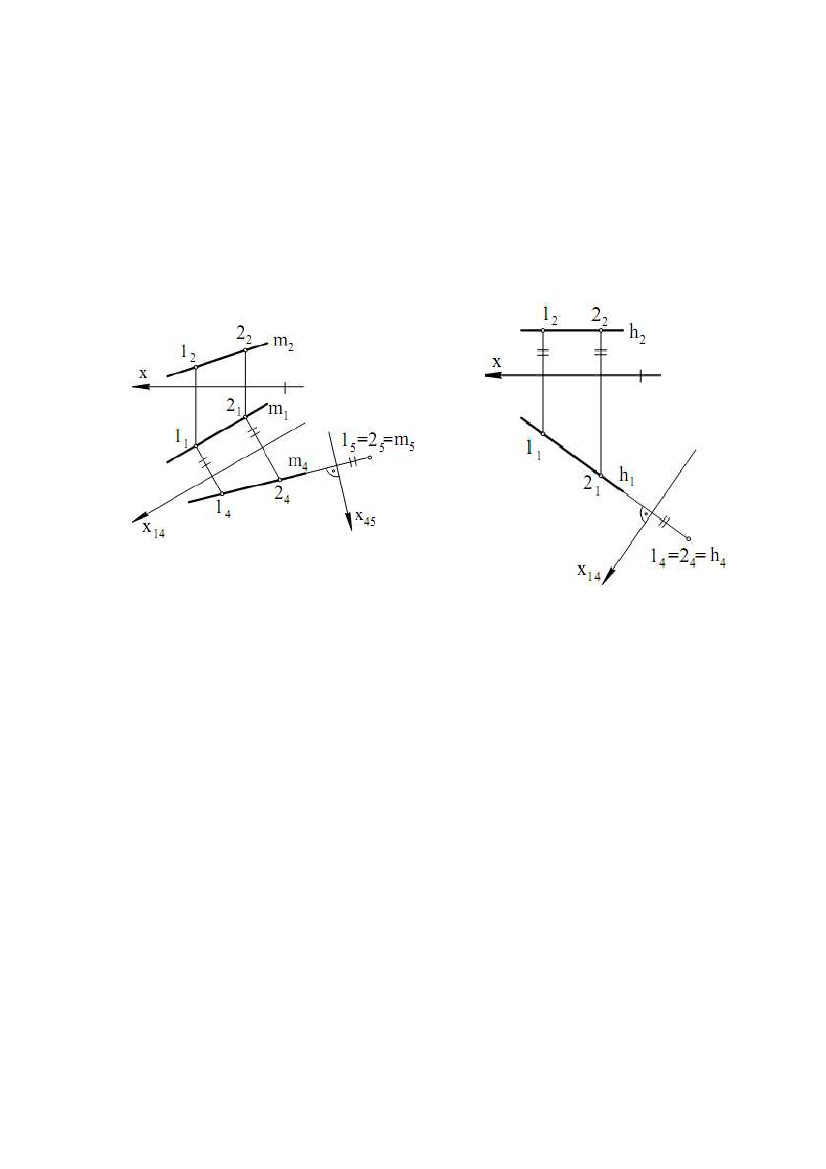

Нехай h(h1, h2) – горизонталь (рис. 4.5). Введемо нову площину проекцій

П4 перпендикулярно до h. Оскільки h паралельна П1, то П4 буде

перпендикулярна П1. Площина П4 може бути взята як нова площина проекцій і

на неї h спроектується в точку. Нова вісь x14 перпендикулярна проекції h1, тому

що h1 паралельна h і, виходить, перпендикулярна П4 і x14. Для побудови нової

проекції горизонталі побудуємо нові проекції двох її точок 1 і 2. Нові проекції

цих точок, побудовані за правилом заміни площин проекцій, збігаються. Тому

що точки 1 і 2 взяті довільно, то проекції інших точок горизонталі теж

збіжаться, тобто горизонталь проектується на П4 у точку.

Рис. 4.5

Рис. 4.6

Використовуючи рішення задачі проектування лінії рівня в точку, можна

виконати проектування прямої загального положення m у точку (рис. 4.6).

Введемо нову площину проекцій П4 паралельно прямій m і перпендикулярно до

П1. Нова вісь x14 паралельна до горизонтальної проекції m1. За новими

проекціями двох довільних точок 1 і 2 прямій m знаходимо m4. У новій системі

площин (П1⊥П4) пряма m є лінією рівня, вона паралельна П4 (при цьому m1

паралельна x14). Тепер, використовуючи рішення попередньої задачі (рис. 4.5),

спроектуємо пряму m в точку. Для цього вводимо нову площину проекцій П5

перпендикулярно до прямої m і перпендикулярно до П4. Пряма m на П5

проектується в точку. У новій системі площин проекцій (П4⊥П5) пряма m є

проектуючою прямою.

1.3. Проектування площини загального положення в пряму на нову

площину проекцій. Знаходження натуральної величини плоскої

фігури

Якщо спроектувати яку-небудь пряму m, що належить площині

загального положення , у точку, то площина спроектується на цю ж

площину проекцій у пряму лінію. Дійсно, пряма m перпендикулярна до

46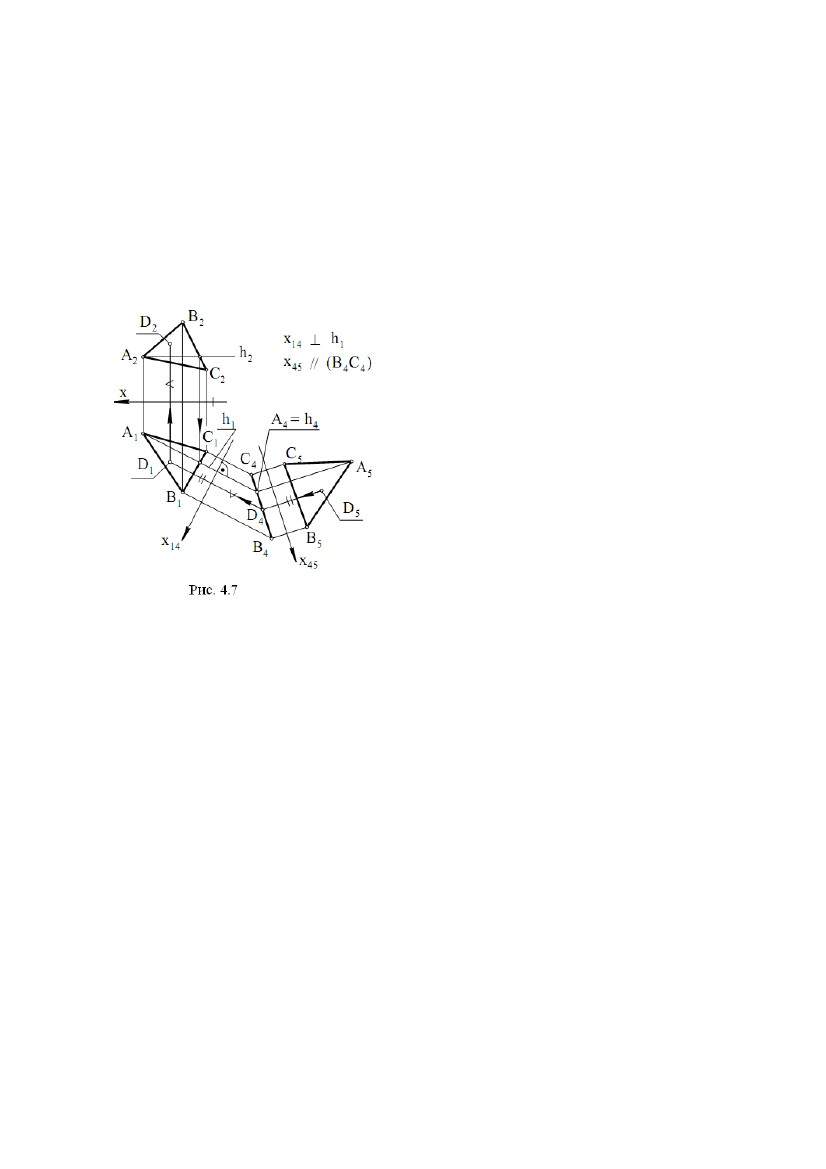

площини проекцій і, виходить, площина проходить через перпендикуляр до

площини проекцій і теж їй перпендикулярна. Площина є проектуючою

площиною і на площину проекцій проектується в пряму. Якщо m - пряма

загального положення, то для проектування її в точку будуть потрібні дві

заміни площин проекцій (рис. 4.6). Якщо m - пряма рівня, то для її

проектування в точку буде потрібна одна заміна площин проекцій (рис. 4.5).

Нехай Σ – площина загального положення, задана трикутником АВС

(рис. 4.7). У площині Σ проведемо горизонталь h, запроектуємо горизонталь h у

точку h4 на площину П4 (x14 ⊥h1, П4 ⊥h), побудуємо нові проекції точок А4, В4,

С4.

Площина Σ проектується в пряму, що

проходить через точки А4, В4, С4.

Площина Σ у системі (П1П4) є

проектуючоюплощиною-вона

перпендикулярна до П4 . Трикутник АВС

проектується на П4 у відрізок В4С4. Для

знаходженнянатуральноївеличини

трикутника АВС введемо площину

паралельнуплощиніпроекційП5

трикутника і перпендикулярно до П4.

Нова вісь x45 паралельна відрізку D4C4

(у протилежному разі Σ і П5

перетнуться). Трикутник АВС

проектується на площину П5 у натуральну величину ∆А5В5С5 = ∆АВС.

Аналогічно визначають натуральну величину будь-якої плоскої фігури.

Площина у системі (П4⊥П5) є площиною рівня. Якщо треба побудувати

в площині Σ яку-небудь фігуру, то виконати цю побудову в площині загального

положення важко. У цьому випадку проводяться побудови, показані на рис. 4.7.

На П5 будують натуральну величину фігури. Потім добудовують інші проекції

цієї фігури. На рис. 4.7 по проекції D5 (одна точка натуральної величини

фігури) знайдені інші проекції цієї точки. Проекція D4 належить прямій, у яку

проектується площина Σ. Послідовність побудов показана стрілками. Правило

заміни площин проекцій справедливе і в цьому випадку. Рівні відрізки

позначені однаково. Таким способом можна побудувати, наприклад, коло,

вписане у трикутник ABC. На площині П5 будуємо коло, вписане в трикутник

А5В5С5, а потім добудовуємо інші проекції ряду точок кола так само, як для

точки D5. Горизонтальна і фронтальна проекції цього кола - еліпси.

У випадку, коли дано проектуючу площину, побудов, пов'язаних з

натуральною величиною фігури, звичайно, менше, тому що площина вже

проектується в пряму лінію. На рис.4.8 показана побудова квадрата, що

належить горизонтально проектуючій площини.

Нехай дано горизонтально проектуючу площину Σ(Σ1) і дві точки цієї

площини А(А1, А2) і В(В1,В2). Необхідно побудувати квадрат ABCD у площині

Σ.

47