Курс лекцій НАРИСНА ГЕОМЕТРІЯ. Курс лекцій удк 514. 18 В.І. Лусь. Нарисна геометрія Курс лекцій. Харків хнамг, 2008. 127 с
 Скачать 5.98 Mb.
|
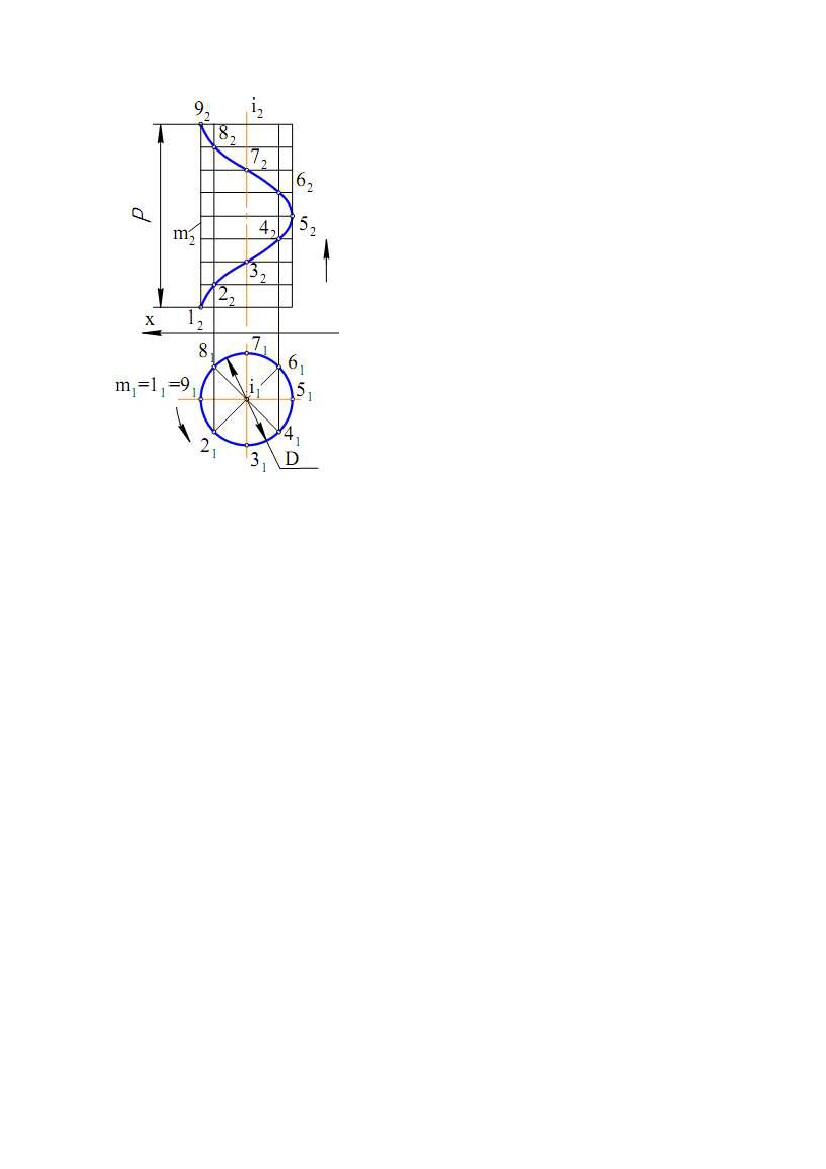 Тоді повороту прямої m на 1/8 частинуобороту відповідатиме лінійне переміщення точки на 1/8 кроку. На рис. 6.7 точка займає положення 2(21, 22). При повороті прямої ще на 1/8 частину оберту, точка підніметься ще на 1/8 частину кроку – точка 3(31, 32) і т.д. Отримані фронтальні проекції точок гвинтової лінії з'єднуємо по лекалу. Якщо обертання прямої навколо осі виконується проти годинникової стрілки, і точка при цьому піднімається вгору, то така гвинтовалініяназиваєтьсяправою гвинтовоюлінією.Якщообертання виконується за годинниковою стрілкою, і точка при цьому піднімається вгору, то гвинтова лінія називається лівою гвинтовою лінією. Пряма m при обертанні навколо осі i описує циліндричну поверхню обертання, Рис. 6.7 тому гвинтова лінія називається циліндричною гвинтовою лінією. Всі точки цієї гвинтової лінії належать циліндричній поверхні обертання. Звернемо увагу на те, що горизонтальною проекцією циліндричної гвинтової лінії є коло, а фронтальною - крива, що називається синусоїдою. Для одержання більш точного креслення гвинтової лінії необхідно коло ділити на більше число частин (n >8). Якщо за тих самих умов утворення гвинтової лінії пряма m перетинає вісь i, то така гвинтова лінія називається конічною гвинтовою лінією. 69 ЛЕКЦІЯ №7. ПОВЕРХНІ. ГРАННІ ПОВЕРХНІ І МНОГОГРАННИКИ. ПОВЕРХНІ ОБЕРТАННЯ. ЦИКЛІЧНІ Й ГВИНТОВІ ПОВЕРХНІ 1. ПОНЯТТЯ ПОВЕРХНІ У нарисній геометрії поверхні розглядаються як множина послідовних положень деякої лінії, що переміщується у просторі за певним законом. Такий спосіб утворення поверхні називається кінематичним. Лінія (крива або пряма) рухається у просторі за певним законом і утворює поверхню. Вона називається твірною. У процесі утворення поверхні вона може залишатися незмінною або міняти форму. Закон переміщення твірної задається у вигляді сукупності ліній і вказівок про характер переміщення твірної. Ці лінії називаються напрямними. Крім кінематичного способу, поверхня може бути задана: • аналітично, тобто описана математичним виразом; • каркасним способом, що використовується при завданні складних поверхонь; каркас поверхні являє собою впорядковану множину точок або ліній, що належать поверхні. Щоб задати поверхню на комплексному кресленні, досить мати на ньому такі елементи поверхні, які дозволяють побудувати кожну її точку. Сукупність цих елементів називається визначником поверхні. Визначник поверхні складається з двох частин: • геометричної частини, що включає постійні геометричні елементи (точки, лінії), які беруть участь в утворенні поверхні; • алгоритмічної частини, що задає закон руху твірної, характер зміни її форми. У символічному вигляді визначник поверхні Φ можна записати у вигляді: Φ(Г) [A], де Г – геометрична частина визначника, А – алгоритмічна. Щоб у поверхні виділити визначник, слід виходити з кінематичного способу її утворення. Але оскільки що багато однакових поверхонь можуть бути отримані різними шляхами, то вони будуть мати різні визначники. Нижче будуть розглянуті найпоширеніші поверхні відповідно до класифікаційних ознак, прийняті в курсі нарисної геометрії. 2. КОНТУР І НАРИС ПОВЕРХНІ Щоб задати поверхню на комплексному кресленні, досить указати проекції не всієї множини точок і ліній, що належать поверхні, а тільки геометричних фігур, що входять до складу її визначника. Такий спосіб задання поверхні дозволяє побудувати проекції будь-якої її точки. Задання поверхні проекціями її визначника не забезпечує наочність, що 70 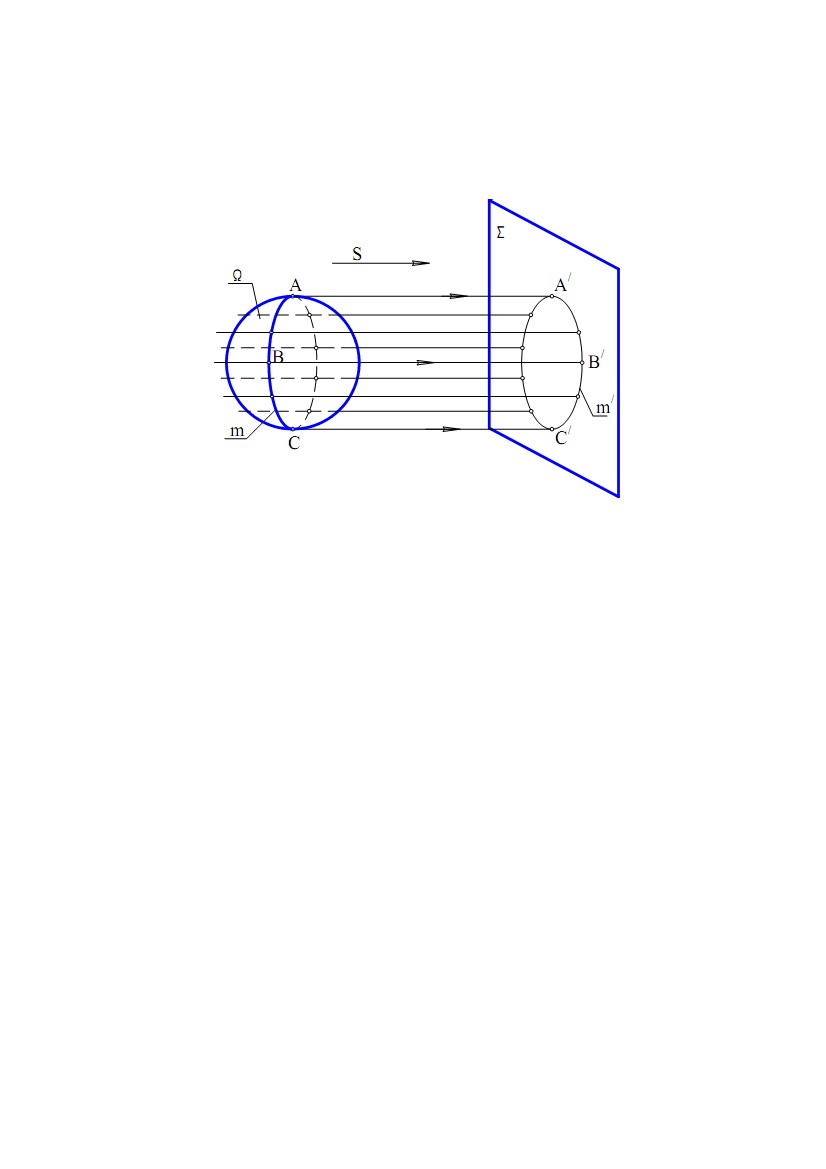 утрудняє читання креслення. Для підвищення наочності, якщо це можливо, накресленні вказують нарисові лінії (нариси) поверхні. Коли яка-небудь поверхняпроектується паралельно на площину проекцій Σ, то проектуючі прямі дотичні поверхні Ωутворять циліндричну поверхню. (рис. 7.1). Рис. 7.1 Ці проектуючі прямі торкаються поверхні Ωу точках, що утворюють деяку лінію m, що називається контурною лінією. Проекція контурної лінії m на площину Σ – m/ називається нарисом поверхні. Нарис поверхні відокремлює проекцію поверхні від іншої частини площини проекцій. Контурну лінію поверхні використовують при визначенні видимості точок щодо площини проекцій. Так, на рис. 7.1 проекції точок поверхні , розташовані ліворуч контуру m, на площині Σ будуть видимими. Проекції інших точок поверхні будуть невидимими. 3. ТОЧКА І ЛІНІЯ НА ПОВЕРХНІ Точка належить поверхні, якщо вона належить якій-небудь лінії, що належить поверхні. Лінія належить поверхні, якщо всі її точки належать поверхні. Отже якщо точка належить поверхні, то і її проекції належать однойменним проекціям деякої лінії цієї поверхні. Для побудови точок, що лежать на поверхнях, користуються графічно простими лініями (прямими або колами) цієї поверхні. У деяких випадках застосовують криві, які проектуються в графічні прості лінії. Приклади побудови відсутніх проекцій точок і ліній, що належать поверхням, розглянуті нижче для кожної класифікаційної групи поверхонь. 71 4. ПОВЕРХНІ (ЗАГАЛЬНІ ВІДОМОСТІ) Із множини різних поверхонь виділяють кілька класів залежно від форми твірної, а також від форми, числа і розташування напрямних: 1) Поверхні закономірні й незакономірні. 2) Лінійчаті (утворені переміщенням прямої лінії) і нелінійчаті (криволінійні) поверхні. 3) Поверхні що розгортаються (або торси) і що не розгортаються. 4) Поверхні з твірною постійної форми і поверхні з твірною змінної форми. 5) Поверхні з поступальним, обертальним або гвинтовим рухом твірної. З усього різноманіття поверхонь тут розглянуті лінійчаті поверхні, гранні, поверхні обертання, циклічні й гвинтові. 5. ЛІНІЙЧАТІ ПОВЕРХНІ Лінійчата поверхня в загальному випадкувизначається трьома напрямними лініями. Тоді визначник такої поверхні має вигляд: Ф(t; k, l, m), де t – прямолінійна твірна; k, l, m – у загальному випадку криволінійні напрямні. Алгоритмічну частину визначника можна записати так: прямолінійна твірна у своєму русі перетинає всі три напрямні. 5.1. Лінійчаті поверхні з двома напрямними і площиною паралелізму В інженерній практиці найбільше поширення одержали лінійчаті поверхні, в яких одна з напрямних є невласною прямою. На кресленні її представником є площина паралелізму. Твірна у своєму русі перетинає дві напрямні й паралельна до деякої площини Σ – площини паралелізму. Такі поверхні називають поверхнями Каталана. Визначник такої поверхні має вигляд Ф(Σ; k, l). Залежно від форми напрямних розрізняють наступні поверхні Каталана: циліндроїд, коноїд і гіперболічний параболоїд (коса площина). Циліндроїд – лінійчата поверхня з площиною паралелізму, в якої обидві напрямні є кривими лініями. На рис. 7.2а показаний відсік (частина) циліндроїда, в якого площина паралелізму Σ – горизонтально - проектуюча. На горизонтальній площині проекцій твірні паралельні між собою і паралельні сліду площини Σ(Σ1). Фронтальні проекції твірних побудовані виходячи з умови перетину напрямних k і l у відповідних точках 1, 2, 3, , 10... У коноїда, на відміну від циліндроїда, одна з напрямних пряма. 72  Гіперболічний параболоїд виходить у результаті переміщення прямої по двохмимобіжних прямолінійних напрямних. Твірна увесь час залишається паралельною площині паралелізму. На рис. 7.2б площина Σ – фронтально - проектуюча і проекції твірних паралельні фронтальному сліду площини Σ(Σ2). Рис. 7.2 Розглянемо приналежність точки поверхням Каталана. Нехай задана фронтальна проекція точки A(A2), що належить поверхні циліндроїда (рис. 7.2а). Потрібно побудувати горизонтальну проекцію точки А. Відповідно до умови приналежності точки поверхні проведемо через А2 проекцію лінії m(m2), що належить циліндроїду. Тому що лінія m належить поверхні, будуємо горизонтальні проекції точок перетину кривої m з твірними циліндроїда. Множина отриманих точок задає горизонтальну проекцію лінії m(m1). Шукана проекція точки А(А1) буде розташована на m1. Нехай тепер фронтальна проекція точки А(А2 ) задана на поверхні гіперболічного параболоїда. І в цьому випадку через А2 можна провести проекцію довільної кривої m. Однак тут відомо, що проекції твірних паралельні сліду площини Σ(Σ2). Тоді через А2 проводимо проекцію твірної KL(K2L2) паралельно Σ2. Горизонтальну проекцію KL проводимо через точки K1 і L1, що належать напрямним k і l, відповідно. Шукана проекція точки А(А1) буде розташована на K1L1. 5.2. Конічна і циліндрична поверхні Конічна поверхня утворюється рухом прямолінійної твірної по криволінійній напрямній. При цьому твірна проходить через деяку нерухому 73  точку S, що називається вершиною (рис. 7.3а).Конічна поверхня є окремим випадком лінійчатих поверхонь загального виду, коли дві напрямні, наприклад l і m, перетинаються в точці S. Геометрична частина визначника конічної поверхні включає напрямну k і вершину S. Залежно від виду напрямної конічна поверхня може бути замкнутою і незамкнутою. Циліндрична поверхня виходить у тому випадку, коли всі прямолінійні твірні проходять через напрямну k і перетинаються в невласній точці S (рис. 7.3, б). Геометрична частина визначника конічної поверхні включає напрямну k і невласну вершину S (напрямний вектор). Циліндрична поверхня також може бути незамкнутою або замкнутою. Рис. 7.3 Точка А належить даним поверхням, тому що вона належить твірним цих поверхонь. На конічній поверхні вона належить твірній 2S, а на циліндричній – твірній t. 5.3. Торс Торс (поверхня з ребром повернення) утворюється рухом прямолінійної твірної, дотичної у всіх своїх положеннях до деякої просторової кривої, названої ребром повернення (від франц. «tors») - кручений). Ребро повернення m є напрямною торса. Торс складається з двох порожнин, розділених ребром повернення (рис. 7.4). 74 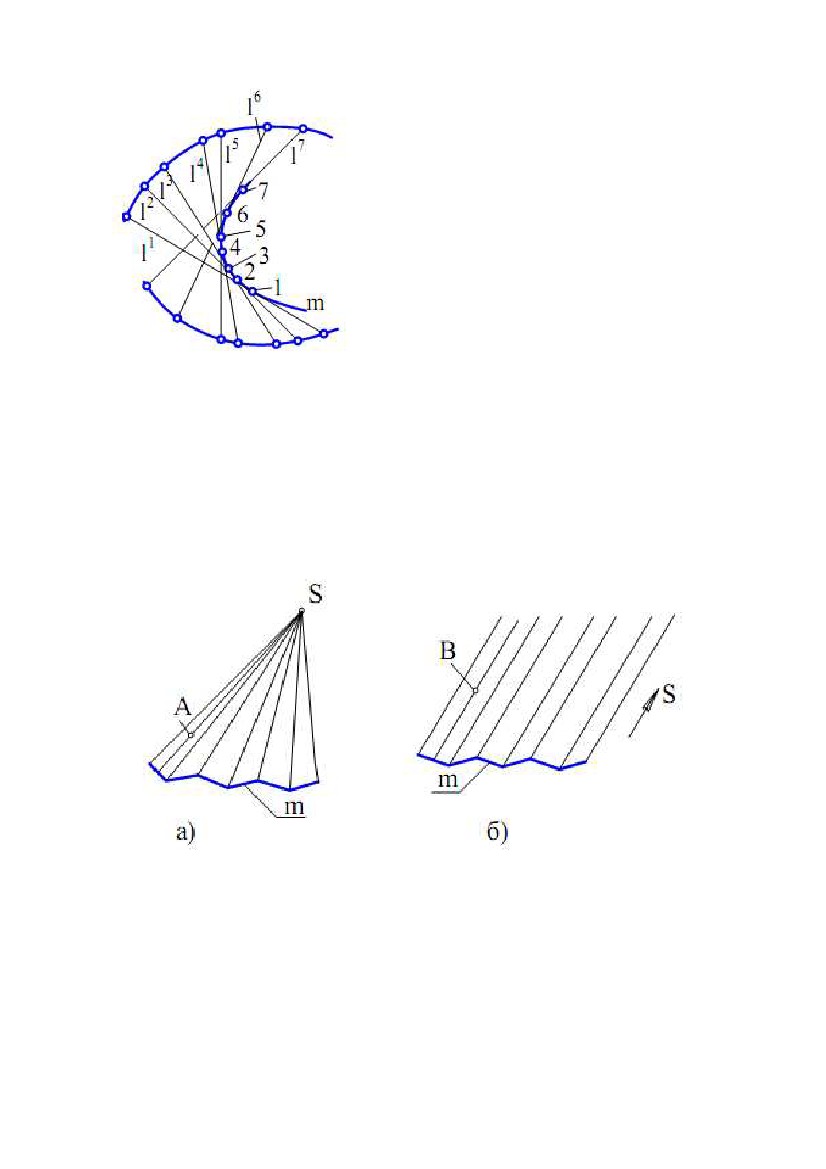 Якщо ребро повернення вироджується вточку, поверхня торса перетворюється в конічну поверхню. У випадку, якщо ребро повернення є невласною точкою, торсова поверхня стає циліндричною Рис. 7.4 6. ГРАННІ ПОВЕРХНІ І МНОГОГРАННИКИ Гранною поверхнею називається поверхня, утворена переміщенням прямолінійної твірної по ламаній напрямній. Гранні поверхні можна розділити на два види: пірамідальні (рис. 7.5а) і призматичні (рис. 7.5б). Рис.7.5 Пірамідальною називається поверхня, утворена переміщенням прямолінійної твірної по ламаній напрямній. При цьому всі твірні проходять через деяку нерухому точку S. Визначник поверхні – ламана напрямна m і точка S. Призматичною називається поверхня, утворена переміщенням прямолінійної твірної по ламаній напрямній. При цьому всі твірні проходять паралельно деякому заданому напрямку S. Визначник поверхні - ламана напрямна m і напрямок S. Точки A і B належать пірамідальній і призматичній 75  поверхням відповідно, тому що належать прямим, розташованим на цихповерхнях. Многогранником називається тіло, поверхня якого складається з кінцевого числа плоских многокутників. Многокутники поверхні називають гранями, сторони многокутників – ребрами, а вершини многокутників – вершинами многогранника. Розглянемо два види многогранників - піраміду і призму. Пірамідаявляєсобою многогранник (рис. 7.6 - це приклад безосного креслення), в якого одна грань−основа(довільний многокутник ABC). Інші грані (бічні) − трикутники із загальною вершиною S, названою вершиною піраміди. Точка D належить поверхні піраміди, тому що лежить на прямій S1, що належить бічній грані ASC. Рис. 7.6 Призмою називається многогранник, в якого основи – рівні многокутники з відповідно паралельними сторонами. Бічні грані призми - паралелограми. Якщоребрабічнихграней перпендикулярні до основи, то призму називають прямою. На рис. 7.7 наведене комплексне креслення (безосне, як багато наведено нижче) тригранної призми. Видимість ребра АВ визначена по конкуруючих точках 3 і 4. Точка 4 розташована вище точки 3, а виходить, на П1 проекція точки 3 буде невидимою. Тому що точка 3 належить ребру 12, то воно також буде невидимим. Точка D (рис. 7.7) належить поверхні призми, тому що лежить на прямій 12, що належить поверхні Рис. 7.7 призми. 76  7. ПОВЕРХНІ ОБЕРТАННЯПоверхнею обертання називається поверхня, отримана при обертовому русі твірної (прямої або кривої) навколо нерухомої прямої, названої віссю обертання (рис. 7.8). Геометричною частиною визначника поверхні обертання є твірна і вісь обертання. Кожна точка твірної n при своєму обертанні описує коло, площина якого перпендикулярна до осі i, а центр розташований на осі. Ці кола називаються паралелями (на рис. 7.8 – наприклад, коло 1). Найменша з паралелей (коло 2) називається горлом, а найбільша (коло 3) – екватором. Площина, що проходить через вісь обертання, називається меридіальною, лінія її перетину з поверхнею – меридіаном. Якщо меридіальна площина паралельна площині проекцій, то на цю площину меридіан проектується без Рис. 7.8 спотворення. Такий меридіан називається головним. На кресленні поверхня обертання однозначно задається своїм визначником. Однак для наочності креслення поверхні доповнюють нарисами. На рис. 7.9 показана побудова нарисів для поверхні, заданою віссю i (i ⊥П1) і твірною n. Візьмемо на твірній n(n1, n2) довільну точку 1(11, 12). При обертанні твірної навколо осі i(i1, i2), точка 1 опише коло, площина якого перпендикулярна до осі, а центр розташований на осі. Тому що вісь поверхні перпендикулярна П1, то площина кола паралельна П1 і коло проектується на П1 в коло із центром i1, що проходить через точку 11. На П2 коло проектуєтьсяувідрізокА2В2, перпендикулярний i2 і рівний А1В1 діаметру кола). Точки А2 і В2 належать фронтальному нарису поверхні. Виконавши описані вище побудови для інших точок твірної n і з'єднавши їх плавною лінією, одержимо фронтальний поверхніобертання.нарисm2 Горизонтальним нарисом поверхні єРис. 7.9 коло, що проходить через точки С1, D1. 77  Нижче наведені деякі окремі види поверхонь обертання, для якихпоказана геометрична частина визначника і побудовані їхні нариси. Поверхні, утворені обертанням прямої лінії: а) циліндрична поверхня обертання – отримана обертанням прямої n навколо паралельної їй осі i (рис. 7.10); б) конічна поверхня обертання - утворена обертанням прямої n навколо пересічної з нею віссю i (рис. 7.11); в) однопорожнинний гіперболоїд обертання - це поверхня, отримана обертанням прямої n навколо мимобіжної з нею віссю i (рис. 7.12). Рис. 7.10 Рис. 7.11 Рис. 7.12 Поверхні, утворені обертанням кривих другого порядку (рівняння такої кривої на площині в декартовій системі координат - алгебраїчне другого ступеня): а) сфера - поверхня, утворена обертанням кола навколо прямої, яка проходить через її центр (на рис. 7.13 узята вісь, перпендикулярна до П1); б) тор - поверхня, отримана при обертанні кола навколо осі, яка лежить у площині кола, але не проходить через її центр; якщо вісь не перетинає коло, то така поверхня називається відкритим тором – r > R (рис. 7.14), а якщо перетинає або торкається – то закритим тором – r ≤ R (рис. 7.15); в) еліпсоїд обертання - поверхня, отримана обертанням еліпса навколо його осі; якщо віссю обертання є мала вісь еліпса (рис. 7.16), то виходить стиснутий еліпсоїд обертання, а якщо більша вісь еліпса - то витягнутий еліпсоїд обертання; г) параболоїд обертання - виходить в обертовому русі параболи навколо її осі (рис. 7.17); д) двопорожнинний гіперболоїд обертання - поверхня, утворена обертанням гіперболи навколо її дійсної осі (рис. 7.18); 78 |