Курс лекцій НАРИСНА ГЕОМЕТРІЯ. Курс лекцій удк 514. 18 В.І. Лусь. Нарисна геометрія Курс лекцій. Харків хнамг, 2008. 127 с
 Скачать 5.98 Mb.
|
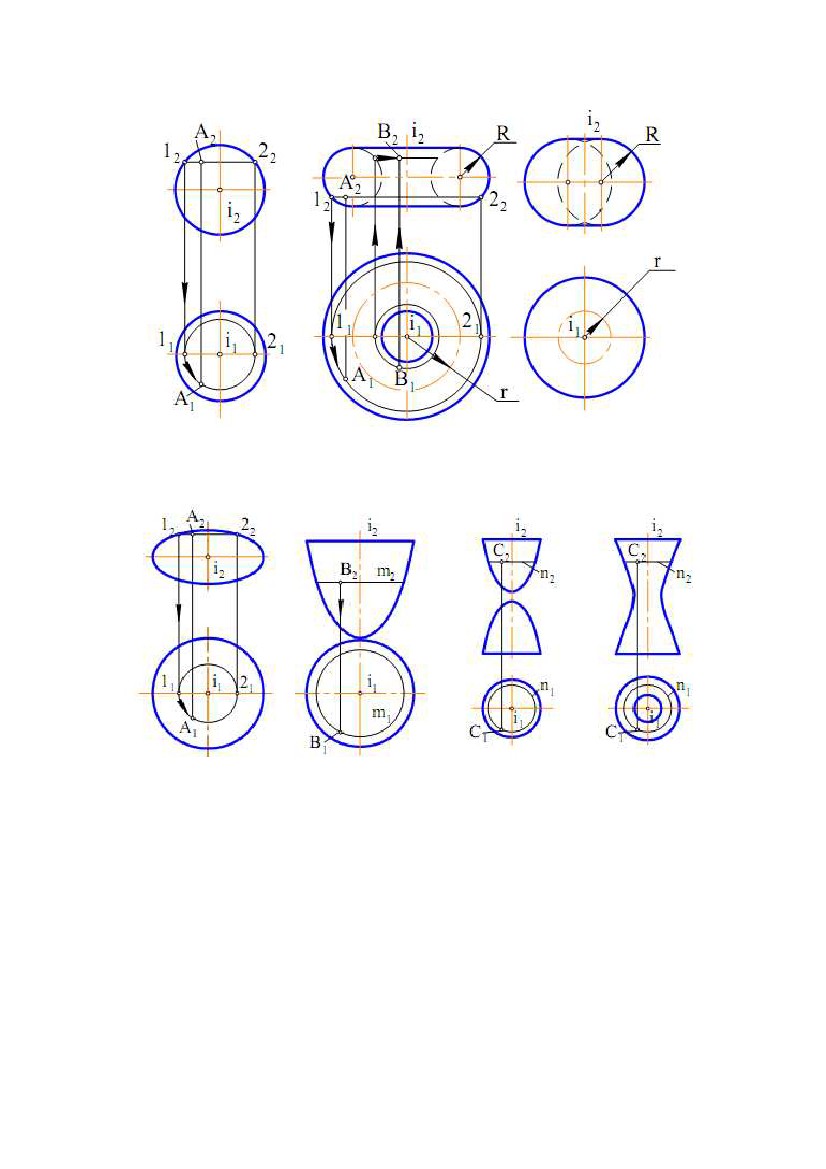 Рис.7.13Рис.7.14 Рис.7.15 Рис.7.16 Рис.7.17 Рис.7.18 Рис.7.19 e) однопорожнинний гіперболоїд обертання - поверхня, утворена обертанням гіперболи навколо її уявної осі (рис. 7.19). 8. ПРИНАЛЕЖНІСТЬ ТОЧКИ І ЛІНІЇ ПОВЕРХНІ ОБЕРТАННЯ При вирішенні задач на приналежність точки поверхні обертання як графічно прості лінії найбільш часто використовують кола. Відомо, що точка належить поверхні, якщо вона належить якій-небудь лінії поверхні. Для циліндричної поверхні обертання найбільш простими 79 лініями є прямі (твірні) і кола. Отже якщо потрібно знайти горизонтальну проекцію точки A(А1) (по відомій фронтальній проекції А2), що належить циліндричної поверхні, то потрібно через точки провести одну з цих ліній. На рис. 7.10 через А2 проведена прямолінійна твірна n(n2). Тому що пряма n займає горизонтально - проектуюче положення, то на П1 вона проектується в точку n1 (вважаємо, що проекція твірної на П2 видима). Тоді в цю ж точку проектується і точка А(А1). З іншого боку, всі кола циліндричної поверхні проектуються на П1 в одне коло, тому що вісь поверхні перпендикулярна до П1. Отже шукана проекція точки А(А1) буде перебувати на цьому колі. Через точку на конічній поверхні обертання можна також провести пряму і коло. На рис. 7.11 через А2 проведені проекції твірної n(n2) і кола 1222. Відрізок 1222 дорівнює діаметру кола. Після побудови горизонтальних проекцій цих ліній, визначаємо по лінії проекційного зв'язку горизонтальну проекцію точки А(А1). Вважаємо, що на П2 проекція точки А(А2) – видима (перебуває перед контуром поверхні відносно П2). Якщо дано горизонтальну проекцію А1, а потрібно знайти А2, то побудови виконуються у зворотній послідовності. Побудови горизонтальних проекцій точок по їхніх фронтальних проекціях за умови, що точки належать відповідним поверхням, показані на рис. 7.13, 7.14, а також на рис. 7.16 - 7.18. Як лінії поверхонь використовують кола (траєкторії точок твірних). Лінія належить поверхні, якщо всі її точки належать поверхні. Якщо відома одна проекція лінії, що належить поверхні, і потрібно побудувати другу її проекцію, то треба на відомій проекції вибрати кілька точок, побудувати відсутні проекції і отримані проекції з'єднати лінією. Вибір кількості точок залежить як від розмірів зображення, так і від складності кривої. У більшості випадків чим більше точок вибирається на вихідній проекції, тим вище точність побудов другої проекції. На рис. 7.20 показаний відсік конічної поверхні обертання і лінія n на цій поверхні. Якщо відомо n1, то для побудови n2 можна використати як прямолінійні твірні поверхні, так і кола. На рис. 7.20 фронтальна проекція лінії n (n2) побудована за допомогою кіл. Профільна проекція лінії n(n3) побудована по точках ліній n1 і n2. Буквами позначені характерні точки лінії (крайні точки, а також приналежні нарисовим утворюючі поверхні), а цифрами - проміжні. Для встановлення видимості проекцій лінії використаємо контури t, m і k поверхні. Так, при проектуванні на П1 лінія n видима, тому що розташована вище горизонтального контуру t(t1, t2). Це видно на фронтальній проекції. При проектуванні на П2 видимою буде ділянка E4CAB (E242C2A2B2), тому що вона розташована перед фронтальним контуром m. Це виходить з горизонтальної проекції. Тоді ділянка, що залишилася, n2 буде невидимою. Видимість профільної проекції лінії n установлюється при погляді спостерігача на площину П3. Ділянка E4C(E343C3), розташована за профільним контуром k, буде невидимою, а що залишилася – видимою. Це можна встановити по горизонтальній або фронтальній проекціях. 8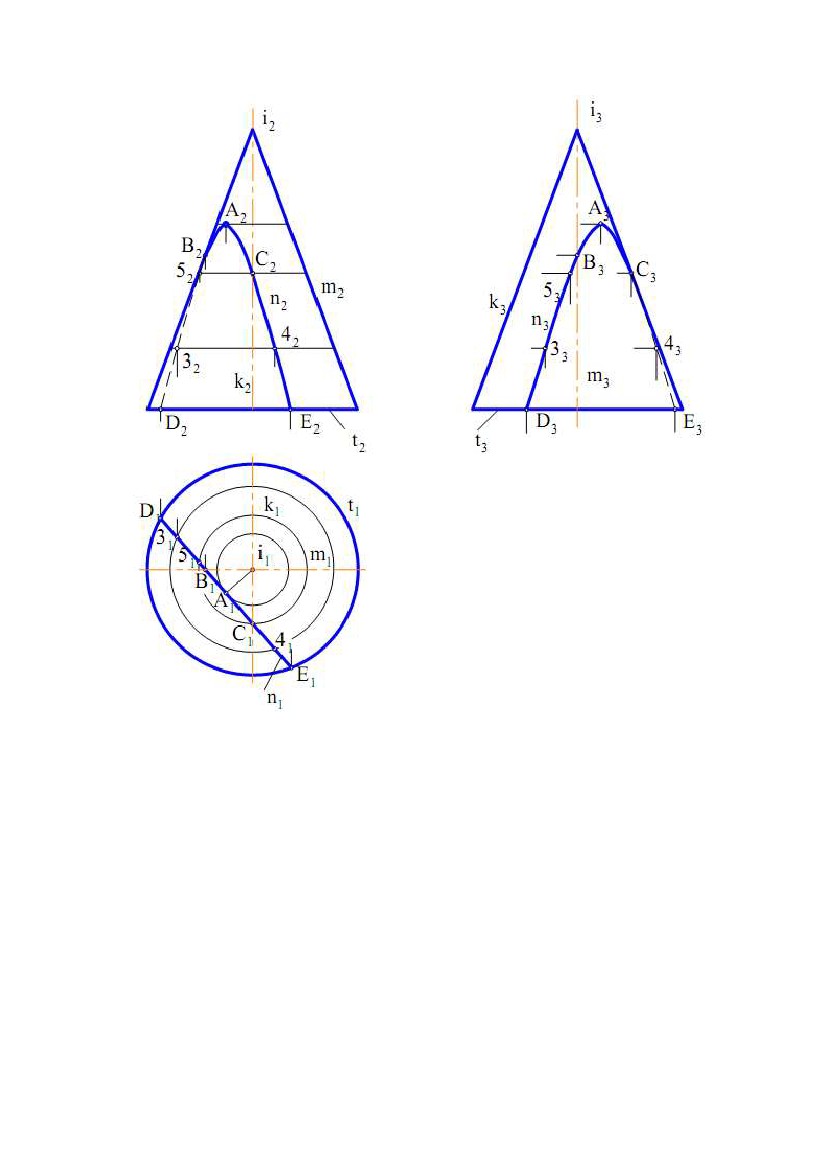0  Рис. 7.209. ЦИКЛІЧНІ ПОВЕРХНІ Циклічна поверхня - це множина послідовних положень кола постійного або змінного радіуса, що переміщається у просторі. Циклічна поверхня загального вигляду задається трьома напрямними m, n і k. Одна з них (n) задає положення центрів кіл, інша (m) – положення площин кіл, а третя (k) – радіуси кіл. Зокрема, площини кіл можуть бути перпендикулярні до напрямної m. Відстань від центра кола до точки перетину площини кола з напрямною k є радіусом цього кола. Якщо одна з напрямних, що задає площини кіл, пряма, то всі кола будуть паралельні до деякої площини, а отримана при цьому поверхня називається циклічною поверхнею з площиною 81 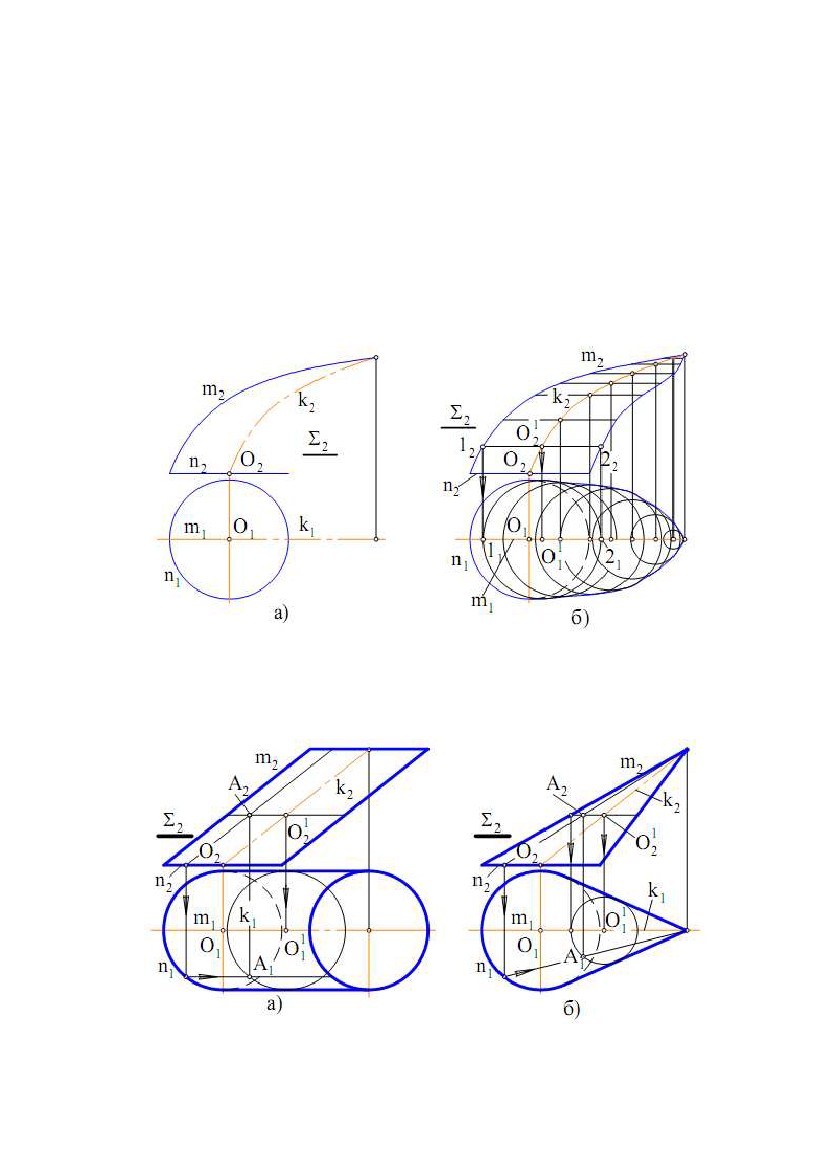 паралелізму. На рис. 7.21,а наведений визначник Ф(k, m, Σ) такої поверхні.Твірною є коло n(n1, n2). Та ж поверхня з побудованим горизонтальним нарисом і добудованим фронтальним показана на рис. 7.21б. Побудови нарисів виконані в такій послідовності. Через довільну точку O21 напрямної k проведений відрізок O2112. Точка O21 – фронтальна проекція центра кола, а відрізок O2112 – його радіус. Для побудови точки 22 від O21 відкладаємо відрізок O2112, а на П1 по лінії проекційного зв'язку визначаємо точку O11 . Будуємо коло із центром O21 і радіусом O2112. Для одержання відсутнього фронтального нарису будуємо ряд точок, аналогічно точці 22. Потім ці точки з'єднуємо. Горизонтальний нарис поверхні являє собою обгинаючу множини кіл, побудованих за аналогією з описаною вище. Рис.7.21 Окремими видами циклічної поверхні з площиною паралелізму є поверхні, в яких напрямні m і k прямі. На рис. 7.22,а показана поверхня, названа еліптичним циліндром, а на рис. 7.22,б - поверхня еліптичного конуса. Рис.7.22 82 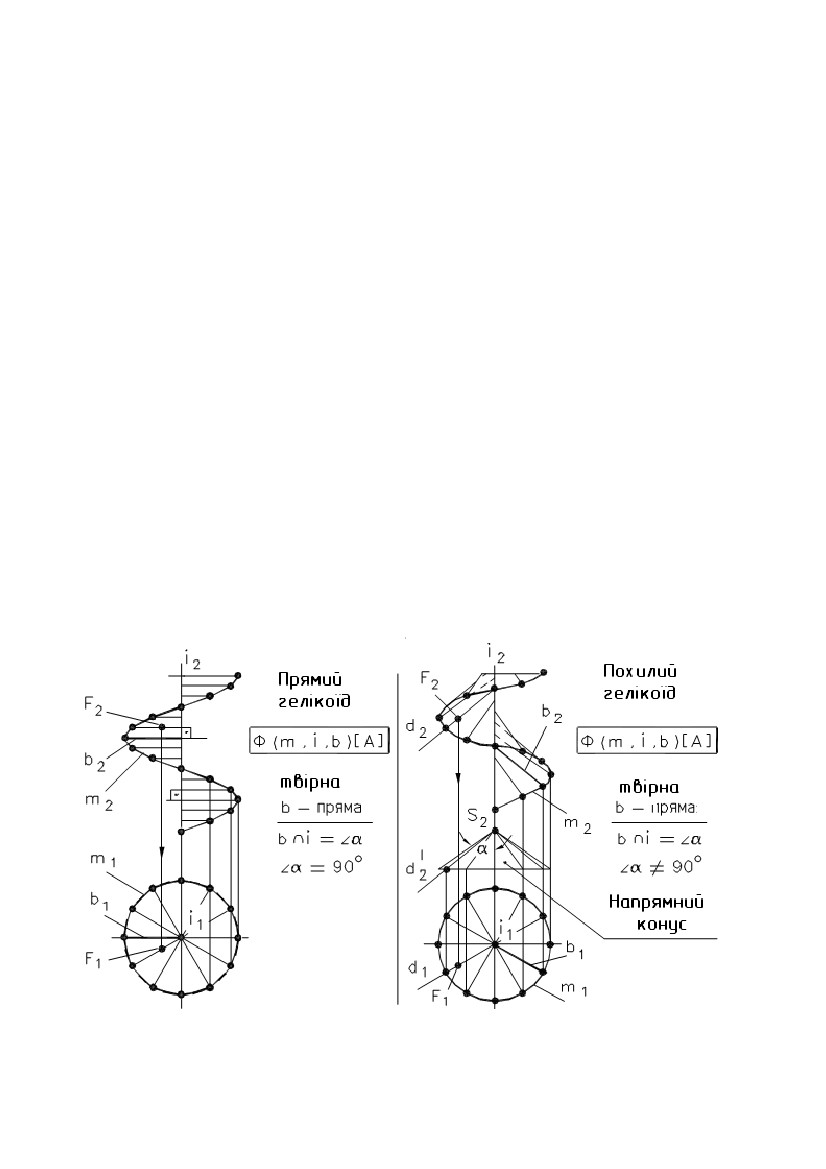 Там же показана побудова горизонтальної проекції точки А по відомійфронтальній. Як лінії поверхні використані прямолінійна твірна і коло. 10. ГВИНТОВІ ПОВЕРХНІ Гвинтовою поверхнею називається поверхня, що описується якою- небудь лінією (твірною) при її гвинтовому русі. Гвинтовим рухом називається складний рух, що складається з рівномірного обертового руху навколо осі і рівномірного прямолінійного руху, паралельного до цій осі. При гвинтовому русі точки виходить гвинтова лінія (див. рис. 7.23). Якщо твірною гвинтової поверхні є пряма лінія, то поверхня називається лінійчатою гвинтовою поверхнею, або гелікоїдом. Гелікоїд називається прямим або похилим залежно від того, перпендикулярна твірна до осі гелікоїда чи нахилена. Розглянемо деякі види лінійчатих гвинтових поверхонь. 1) Прямий гелікоїд утворюється рухом прямолінійної твірної m по двох напрямних. Одна з напрямних є циліндричною гвинтовою лінією m, а інша − її віссю i. Причому у всіх своїх положеннях твірна m паралельна до площини, що називається площиною паралелізму. У прямого гелікоїда твірна m перетинає гвинтову вісь i під прямим кутом. Прямий гелікоїд відноситься до числа коноїдів і називається гвинтовим коноїдом. Рис. 7.23 83 2) Похилий гелікоїд відрізняється від прямого гелікоїда тим, що його твірна m перетинає вісь гелікоїда під постійним кутом, не рівним прямому куту. У похилого гелікоїда одна з напрямних є циліндричною гвинтовою лінією m, а інша − її віссю i . У всіх своїх положеннях твірна b паралельна до твірної деякого конуса обертання. У цього конуса кут між твірною і віссю, паралельною до осі гелікоїда, дорівнює α. Він називається напрямним конусом похилого гелікоїда (рис.7.23). 3) Розгортний гелікоїд утворюється рухом прямолінійної твірної b, що торкається у всіх своїх положеннях циліндричної гвинтової лінії m. Вона є ребром повернення гелікоїда. Розгортний гелікоїд, як лінійчата поверхня з ребром повернення, відноситься до числа торсів. 84 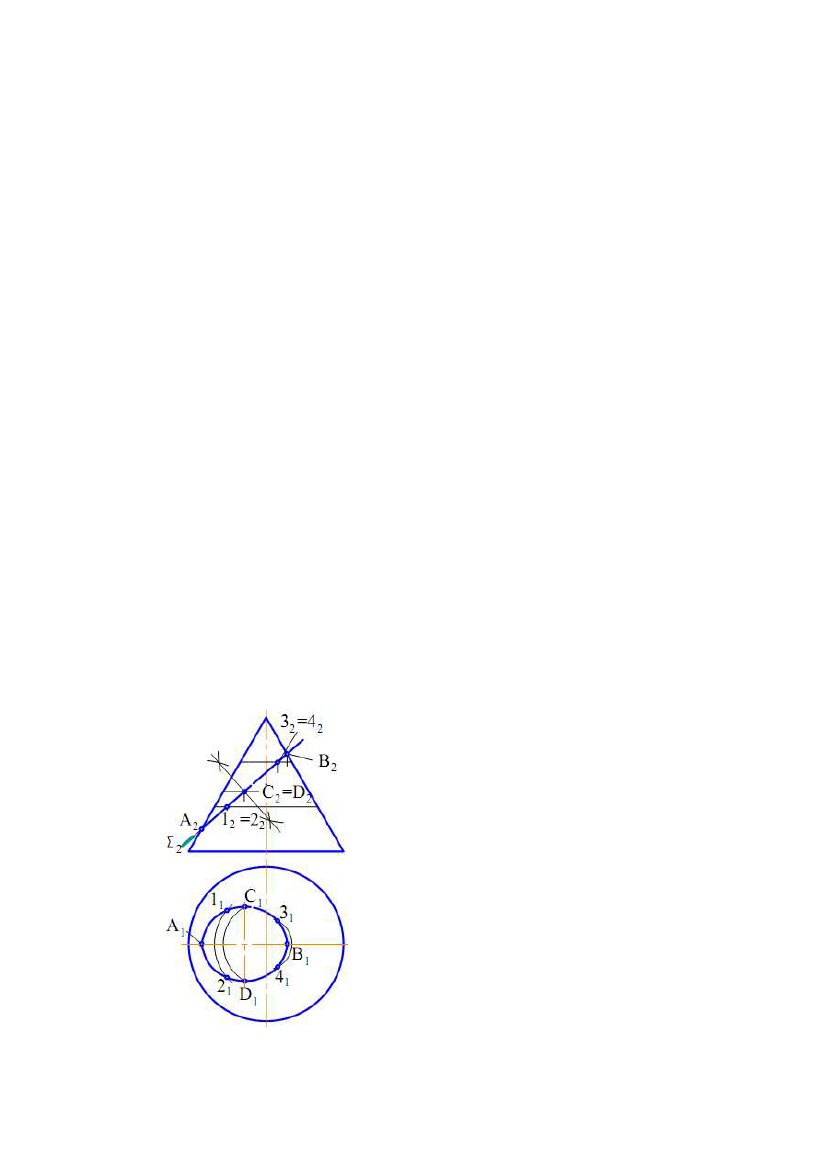 ЛЕКЦІЯ № 8. ПОБУДОВА ПЕРЕТИНУ ФІГУР. ПЕРЕТИНПОВЕРХОНЬ 1. ПЕРЕТИН ПОВЕРХНІ І ПЛОЩИНИ Лінія перетину поверхні з площиною являє собою лінію, названу перетином. Точки цієї кривої можна розглядати як точки перетину ліній поверхні з площиною або прямих площини з поверхнею. Звідси випливають два варіанти побудови перетину: 1) вибираємо кінцеве число ліній на поверхні й визначаємо точки перетину їх із площиною; 2) виділяємо кінцеве число прямих на площині і будуємо точки перетину їх з поверхнею. Зазначимо, що можливо вирішення, яке являє собою комбінацію цих варіантів. У кожному разі побудова перетину зводиться до багаторазового застосування алгоритму вирішення задачі на перетин лінії і поверхні. Визначення проекцій ліній перетину рекомендується починати з побудови його опорних (характерних) точок. До них відносяться точки, розташовані на нарисових твірних поверхні (вони визначають межу видимості проекцій кривої), точки, віднесені на екстремальні відстані від площин проекцій та деякі інші. Після цього визначають проміжні точки перетину. Побудова перетину істотно спрощується, якщо площина займає проектуюче положення. Це пов'язане з тим, що проектуюча площина характеризується збірною властивістю. У цьому разі одна з проекцій перетину перебуває на сліді площини, тобто відома. Приклад 1. Побудувати проекції перетину конічної поверхні обертання з фронтально - проектуючою площиною (рис. 8.1). Вирішення. Задана площина Σ перетинає вихідну поверхню по еліпсі, фронтальна проекція якого розташована на сліді цієї площини. Горизонтальну проекцію перетину будуємо по точках відповідно до задачі на приналежність лінії поверхні (див. рис. 8.1). Проекцію еліпса на площині Π1 можна побудувати також по його великій Α1Β1 і малій C1D1 осях. Фронтальна проекція малої осі еліпса (точки C2=D2) розташована на середині відрізка А2В2. Рис. 8.1 85 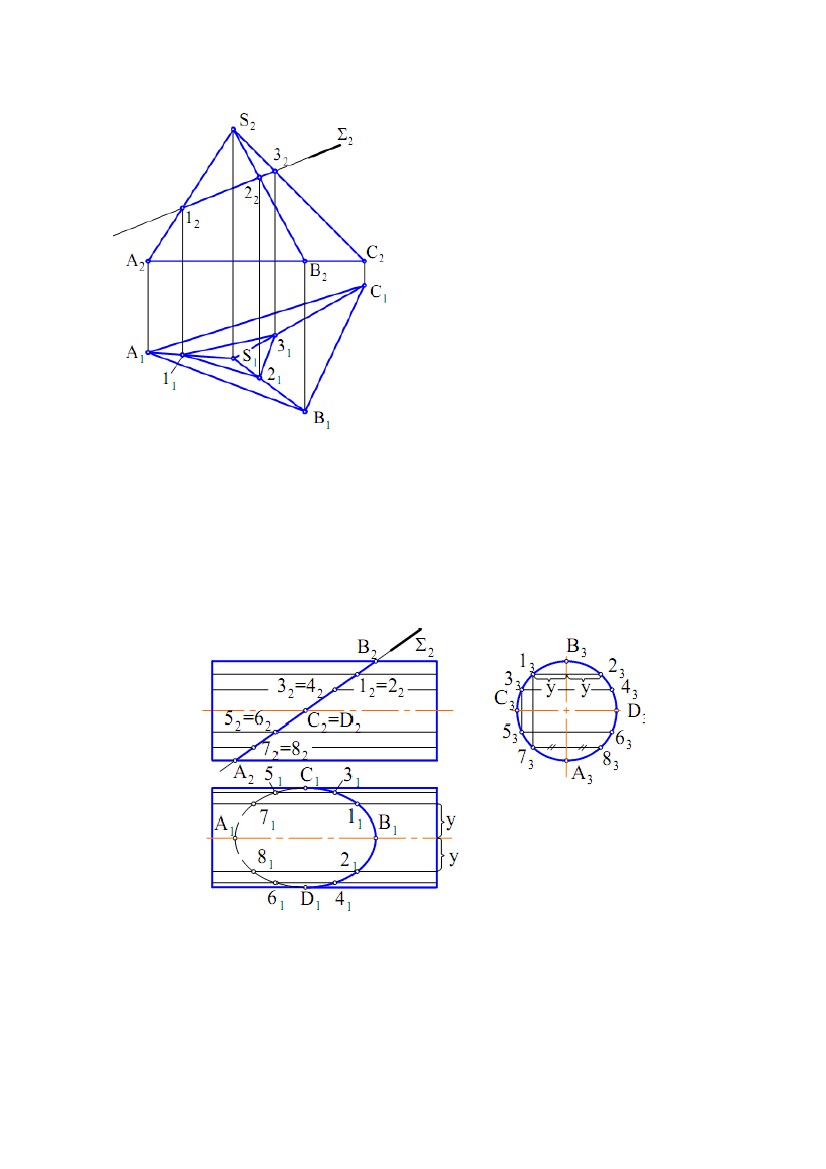 Приклад 2. Побудувати перетин многогранника площиною (рис. 8.2).У перетині гранних поверхонь площинами виходять многокутники. Їхні вершини визначаються як точки перетину ребер гранних поверхонь із січною площиною. Многокутник перетину може бути побудований двома способами: 1) Вершини многокутника знаходяться як точки перетину прямих (ребер) із січною площиною; 2) Сторони многокутника визначають як лінії перетину граней (площин) многогранника із січною площиною. На рис. 8.2 показана побудова перетину піраміди площиною Σ. Січна площина є Рис. 8.2 що фронтально - проектуючою, отже всі лінії, що лежать у цій площині, збігаються з фронтальним слідом Σ2 площини Σ. Отже фронтальна проекція 122232 перетину визначиться при перетині фронтальних проекцій ребер піраміди із слідом Σ(Σ)2. Горизонтальні проекції точок 1(11), 2(21) і 3(31) знаходимо з умови приналежності точок ребрам піраміди. Приклад 3. Побудувати лінію перетину циліндричної поверхні обертання з площиною Σ(Σ)2 (рис. 8.3). Рис.8.3 Вирішення. Спочатку знаходимо опорні точки A(A1, A2), B(B1, B2), C(C1, C2) і D(D1, D2). Точки А і В визначають у перетині твірного фронтального контуру поверхні й площини Σ (спочатку визначаємо A2 і B2, а потім по лініях проекційного зв'язку – A1 і B1). Точки С і D є точками перетину горизонтального контура поверхні й площини Σ. На П2 горизонтальний контур 86 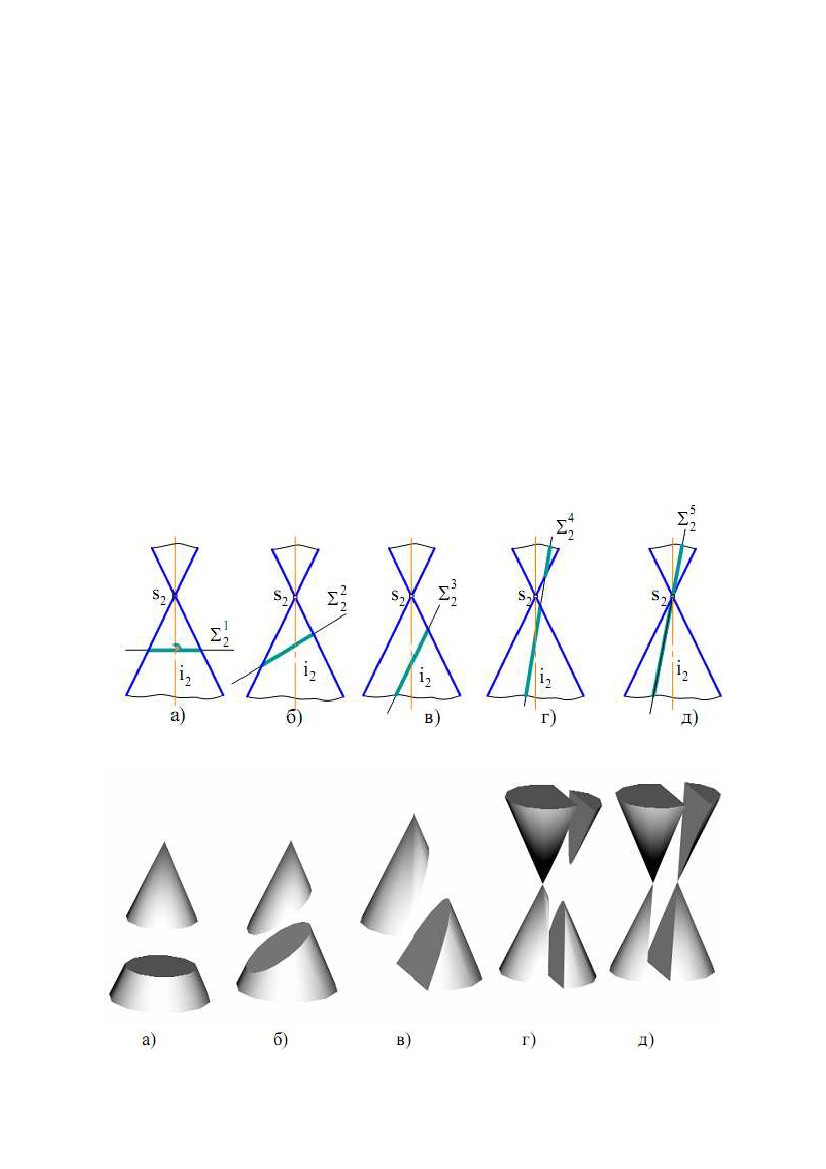 збігається з проекцією осі поверхні обертання, а на П1 є нарисом. Тоді спочаткубудуємо C2 і D2, а потім C1 і D1. Точки 1(11, 12), 2(21, 22), …, 8(81, 82) – це проміжні точки перетину. Вони побудовані введенням проміжних прямолінійних твірних поверхні. Спочатку проводимо проекції твірних на П2, наприклад через точки 12, 22 (твірні – фронтально конкуруючі). На П3 ці твірні проектуються в точки 13 і 23. Горизонтальні проекції твірних побудовані по двох заданих, як показано на рис. 8.3, відклавши відповідні значення координати Y. 2. ПЕРЕТИН КОНІЧНОЇ ПОВЕРХНІ ОБЕРТАННЯ ПЛОЩИНОЮ Залежно від напрямку січної площини в перетині конічної поверхні обертання можуть вийти різні лінії. Вони називаються конічними перерізами. На рис. 8.4 наведена фронтальна проекція конічної поверхні обертання (вісь i паралельна П2) і фронтально проектуючі площини Σ21 , Σ 22...…, Σ25. На рис. 8.5 показані наочні зображення результатів перетину площинами тіл, обмежених конічною поверхнею обертання. Рис. 8.4 Рис.8.5 87 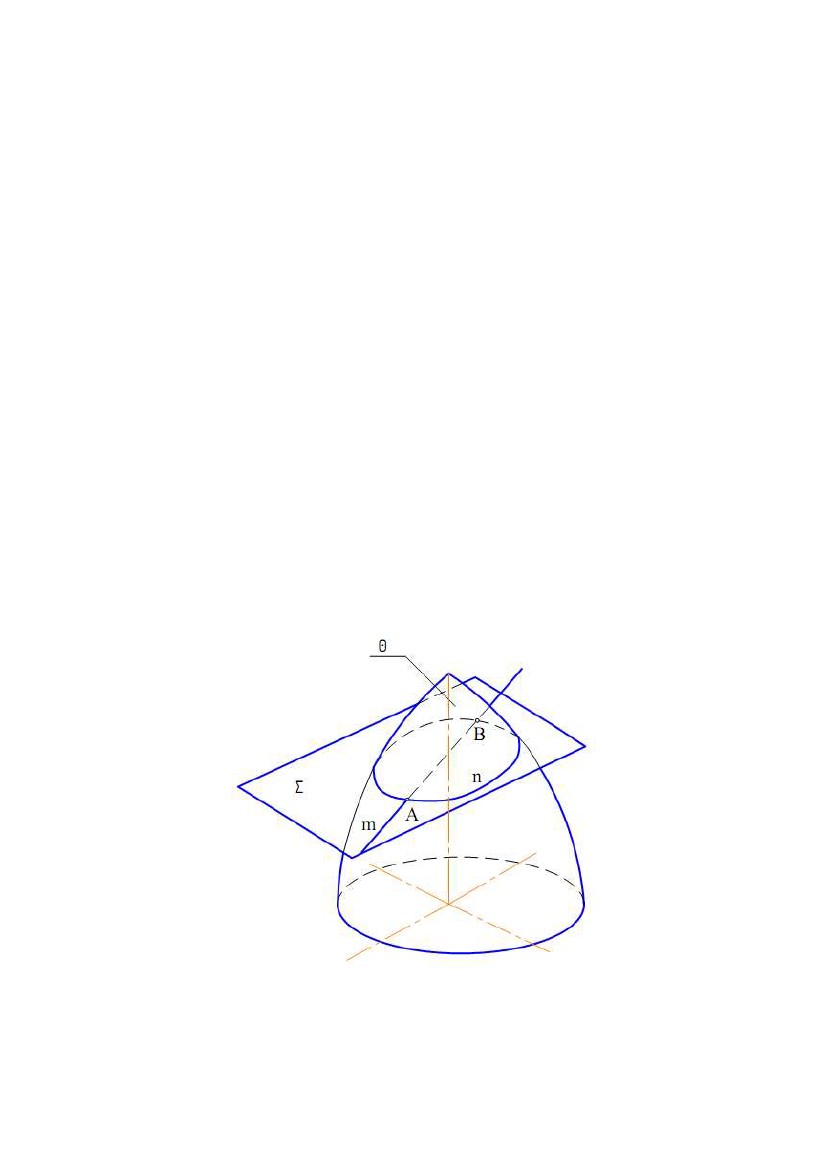 У результаті перетину конуса площиною, перпендикулярної до осіконуса, виходить коло (рис. 8.4,а; 8.5,а). Еліпс виходить у тому випадку, якщо січна площина перетинає всі твірні поверхні і не перпендикулярна до осі i (рис. 8.4,б; 8.5,б). Площина Σ23 паралельна до однієї твірної поверхні і перетинає одну половину конічної поверхні. Перетином є парабола (рис. 8.4,в; 8.5,в). Площина Σ24 паралельна двом твірним і перетинає обидві половини конічної поверхні (перетин – гіпербола) (рис. 8.4,г; 8.5,г). Площина Σ25 проходить через вершину конічної поверхні (перетин – дві пересічні прямі) (рис. 8.4,д; 8.5,д). 3. ПЕРЕТИН ЛІНІЇ І ПОВЕРХНІ Лінія і поверхня перетинаються в загальному випадку в декількох точках А, В, . Алгоритм їх визначення може бути побудований на тих же міркуваннях, що й при побудові точки перетину прямої і площини. Дійсно, точки Α, Β, … перетину лінії m і поверхні Θ належать також лініям, що проходять через ці точки й лежать на заданій поверхні. Криву n можна розглядати як проекцію лінії m на поверхню Θ. Тоді, у випадку паралельного проектування, лінії n і m будуть розташовуватися на одній циліндричній поверхні, в якої напрямною є крива m, а твірні паралельні напрямку проектування. Якщо лінія пряма, то n і m перебувають в одній площині Σ (рис. 8.6). Якщо напрямок Рис. 8.6 проектування буде перпендикулярним до якої-небудь площини проекцій, лінії n і m будуть конкуруючими щодо відповідної площини проекцій. 88 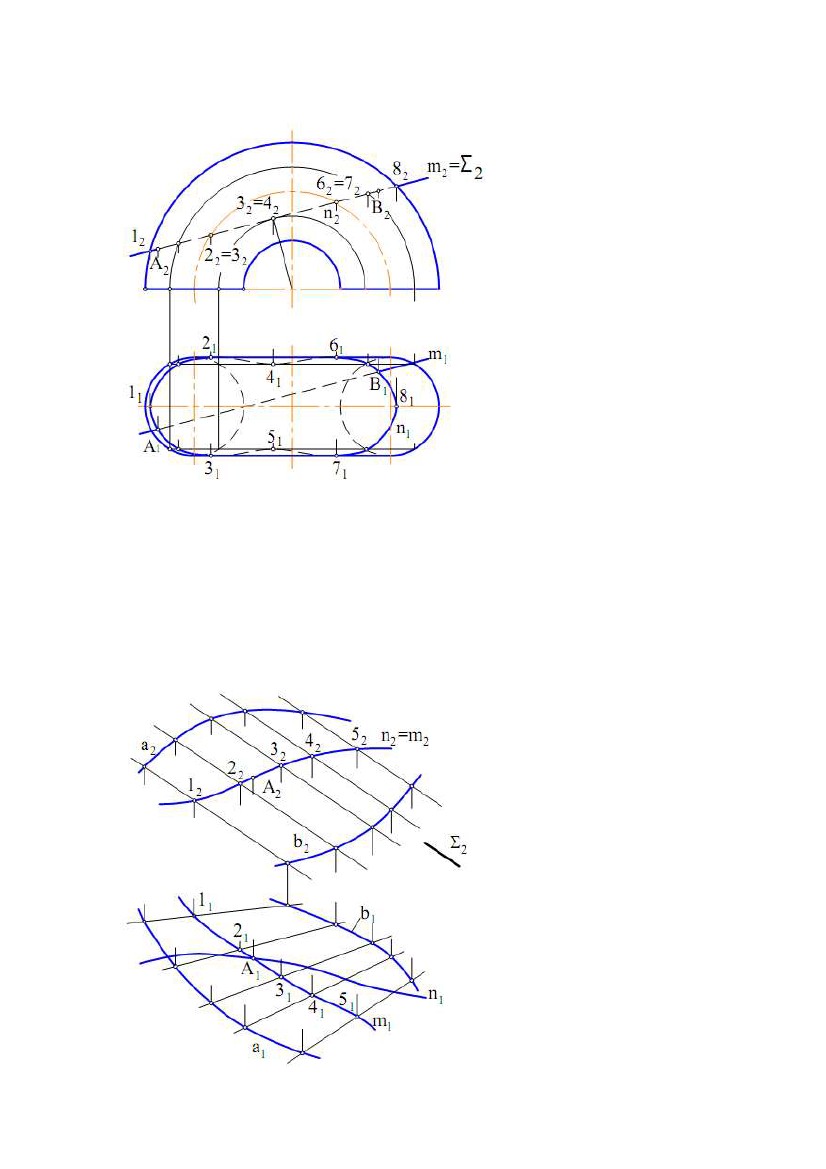 Приклад 1. Дано пряму m і тор. Побудувати точки перетину прямої іповерхні (рис. 8.7). Вирішення. 1) Вибираємо на заданій поверхнілініюn, наприклад, що фронтально конкуруєіззаданою прямою m. Лінії n і m перетинаються, тому що вони перебувають в одній фронтальнопроектуючій площині. 2)Визначаємо горизонтальнупроекцію лінії n (n1), виходячи з умови приналежності її поверхні. 3) Знаходимо точки Α і Β перетину ліній n і m, які і є Рис. 8.7 шуканими. 4) Установлюємо видимість проекцій прямій. Так, як ділянка ΑΒ прямої m, розташована усередині поверхні, то вона невидима на Π1 і Π2. Крім цього, на Π2 невидимий відрізок прямої m правіше точки Β2 до точки на нарисі поверхні, а на Π1 – лівіше точки 51, також до точки на нарисі поверхні. Ці відрізки закриті поверхнею - перебувають за контурами поверхні. Приклад 2. Дано криву n і циліндроїд Γ(a, b, Σ) (рис. 8.8). Побудувати точки перетину лінії і поверхні. Вирішення. 1) На поверхні циліндроїда вводимокривуm,що фронтально конкурує з лінією n. Ці криві перетинаються (у загальному випадку), тому що розташованінаодній циліндричній поверхні, яка є фронтально проектуючою, у якої лінія n - напрямна, а твірні перпендикулярні П2. 2) Будуємо горизонтальну проекцію кривої m(m1) (m⊂Γ).⊂ 3) Знаходимо горизонтальну проекцію точки Α(Α1) - Α1 = n1 ∩ m1, а потім і Α2(Α2 ⊂n2). Рис. 8.8 89 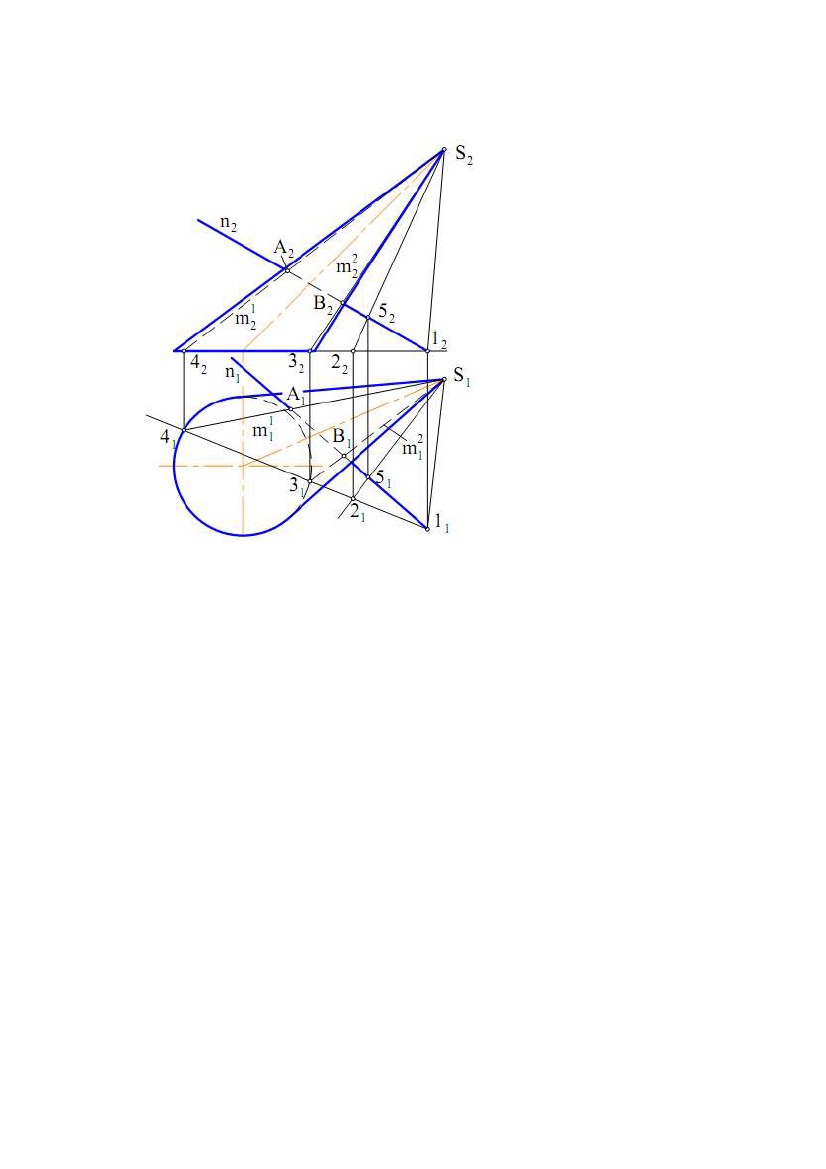 Приклад 3. Дано пряму n і конічну поверхню (рис. 8.9). Побудуватиточки перетину лінії і поверхні. Вирішення. Поставлену задачуможнатакож розв'язати,задавшина конічній поверхні лінію m, що конкурує із прямою n щодо площини проекцій Π1 або Π2. Отримані криві будуть лекальні, що вимагає значних побудов і знижує точність рішення задачі. Тому що задана поверхня лінійчата, то в якості лінії m на поверхні доцільно взяти пряму (або прямі). Тоді алгоритм вирішення задачі буде наступним: 1) Спроектуємо з точки S пряму n на площину Π1, тобто визначимо центральну проекцію прямої n наРис. 8.9 площині Π1. Для цього проводимо два проектуючих променя через точки, 1 і 5 прямої до перетину із площиною проекцій П1. Точки 1 і 2задають центральну проекцію прямої n на Π1. 2) Будуємо твірні m1 і m2 на конічній поверхні, що конкурують із n відносно П1 при її центральному проектуванні. 3) Знаходимо точки Α і Β перетину прямої n з твірними m1 і m2 Точки Α і Β - шукані. 4) Установлюємо видимість проекцій прямої n. 4. ВЗАЄМНИЙ ПЕРЕТИН ПОВЕРХОНЬ Лінія перетину двох поверхонь являє собою в загальному випадку просторову криву. Будь-яка точка цієї лінії належить як першій, так і другій поверхням і може бути визначена в перетині ліній, проведених на цих поверхнях. Тоді маємо наступні варіанти вирішення даної задачі: 1) вибирають на одній з поверхонь кінцеве число ліній і будують точки перетину їх з іншою поверхнею (див. 8.3); 2) виділяють на заданих поверхнях два сімейства ліній і знаходять їхні точки перетину. У другому варіанті виділення пересічних пар кривих виконують за допомогою допоміжних поверхонь посередників. 90 |