|
Курс лекцій НАРИСНА ГЕОМЕТРІЯ. Курс лекцій удк 514. 18 В.І. Лусь. Нарисна геометрія Курс лекцій. Харків хнамг, 2008. 127 с
 Розглянемо докладніше алгоритм вирішення задачі з використанням поверхонь Розглянемо докладніше алгоритм вирішення задачі з використанням поверхонь
посередників.
Цей спосіб полягає в наступному.
Нехай дано пересічні поверхні Φ і Ψ
(рис. 8.10). Введемо допоміжну січну
поверхню Θ1. Ця поверхня називається
посередником. Вона перетне поверхні Φ і
Ψ по лініях m1 і k1, відповідно.
Перетин ліній m1 і k1 дасть точку M, що
належить шуканій лінії перетину t, тому
що вона належить обом поверхням.
Вводячи ряд посередників, одержуємо
Рис. 8.10
сімейство точок лінії перетину.
Як поверхні посередники найбільш часто застосовують площини або сфери.
Залежно від виду посередників виділяють наступні найбільш часто
застосовувані способи побудови
лінії перетину двох поверхонь:
а) спосіб січних площин;
б) спосіб сфер.
Посередники вибирають так, щоб
лінії mi і ki можна було легко
побудувати, тобто щоб вони були
графічно простими (прямі або
кола). Завдання спрощується, якщо
одназповерхоньзаймає
проектуюче положення. Тоді ця
поверхня вироджується в коло
(циліндрична) або многокутник
(призматична). Одна з проекцій
шуканої лінії буде перебувати на
виродженій проекції поверхні, а
друга - виходить, відома. Друга
проекція лінії визначається з умови
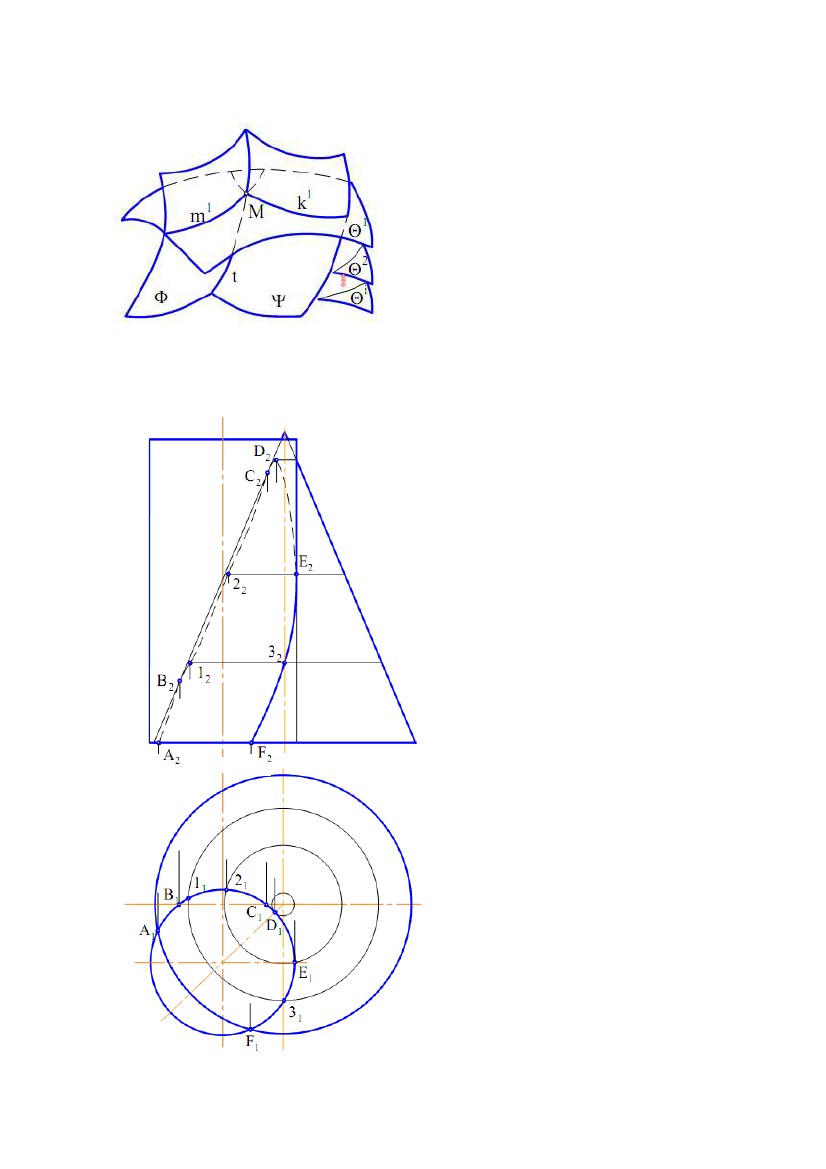
приналежності її поверхні. На рис.
8.11 показана побудова лінії
перетину циліндричної і конічної
поверхонь обертання. Тому що вісь
циліндричноїповерхні
перпендикулярна до П1, то на П1
поверхню проектується в коло. На
це ж коло проектується і шукана
лінія. Точки A, B, C, D, E і F –
опорні точки. Точки А і F належать
горизонтальному, а точка Е –
фронтальному контуруРис. 8.11
91
 циліндричної поверхні На фронтальному контурі конічної поверхні циліндричної поверхні На фронтальному контурі конічної поверхні
розташовані точки В і С. Точка D – екстремальна.
Інші точки лінії перетину, позначені цифрами, - проміжні. Фронтальні
проекції лінії побудовані з умови приналежності її до конічної поверхні.
4.1. Спосіб допоміжних січних площин
Розглянемо застосування допоміжних січних площин на прикладі
побудови лінії перетину сфери з конусом обертання (рис. 8.12, 8.13).
Вирішення. Задані поверхні – поверхні
обертання.Осізаданихповерхонь
паралельні П2, (будь-який діаметр сфери
може бути прийнятий за вісь обертання), а
їхня загальна площина симетрії паралельна
фронтальній площині проекцій. Отже на
заданих поверхнях можна виділити два
сімейства кіл, розташованих у площинах,
паралельних до горизонтальної площини
проекцій. Це значить, що для вирішення
даної задачі можна використати як
посередників горизонтальні площини
Рис. 8.12
рівня.
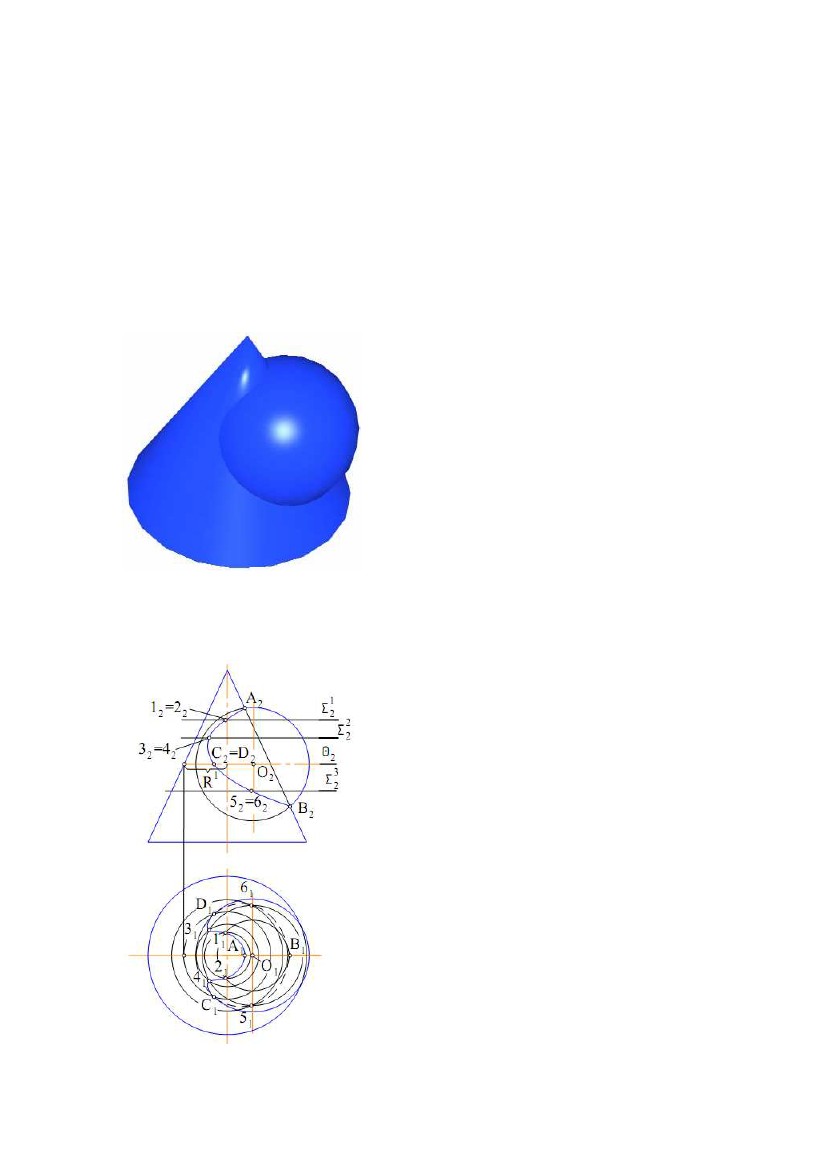
Характерними точками проекцій лінії перетину поверхонь є точки Α, Β і З, D.
Точки Α, Β визначають у перетині нарисових твірних поверхонь, тому що ці
твірні розташовані в спільній площині
симетрії поверхонь. Точки С і D є точками
видимості горизонтальної проекції лінії
перетину. Їхні побудови виконані в такій
послідовності:
1) через центр сфери О проведена
горизонтальна площина рівня Θ;
2) побудована горизонтальна проекція кола
радіуса R1, по якій площина Θ перетинає
конічну поверхню; ця ж площина перетинає
сферу по екватору (колу максимального
радіуса);
3) побудована горизонтальна проекція кола
радіуса R1, по якій площина Θ перетинає
конічну поверхню; ця ж площина перетинає
сферу по екватору (колу максимального
радіуса);
4) визначені точки C1, D1 перетину кола
Рис. 8.13
радіуса R1 з нарисом сфери;
92
 5) визначені фронтальні проекції точок З(З2), D(D2) з умови 5) визначені фронтальні проекції точок З(З2), D(D2) з умови
приналежності їх до площини Θ. Для побудови проміжних точок 1(11,12),
2(21,22), …, 6(61,62) лінії перетину заданих поверхонь використаємо площини
Σ21 , Σ22 і Σ23. Отримані точки з'єднаємо плавною кривою лінією. Видимість
лінії перетину визначається на кожній поверхні окремо. Потім визначаються
ділянки, видимі одночасно для обох поверхонь. Так, при проектуванні конічна
поверхня своїх точок не закриває, а сфера закриває точки, розташовані нижче
горизонтального контуру. Точки С і D, розташовані на горизонтальному нарисі,
відокремлюють видиму частину лінії від невидимої. Невидима частина
показана штриховою лінією. На П2 проекції видимої частини лінії перетину
збігаються з проекцією невидимої, тому що фронтальні нариси обох поверхонь
розташовані в площині симетрії поверхонь.
4.2. Спосіб концентричних сфер
Цей спосіб широко використовують при вирішенні задач на побудову
ліній перетину поверхонь обертання з пересічними осями. В основі цього
способу лежить наступна властивість поверхонь обертання: дві співвісні
поверхні обертання перетинаються по колах, число яких дорівнює числу точок
перетину їх напівмеридіанів. Ці кола лежать у площинах, перпендикулярних до
осі поверхонь обертання. У сфери будь-який діаметр можна прийняти за вісь
обертання. Отже сфера з центром на осі поверхні обертання перетинає цю
поверхню по одному або декількох колах.
Якщо вісь поверхонь обертання паралельна до площини проекцій, то на
цю площину лінія перетину проектується у відрізок прямої лінії.
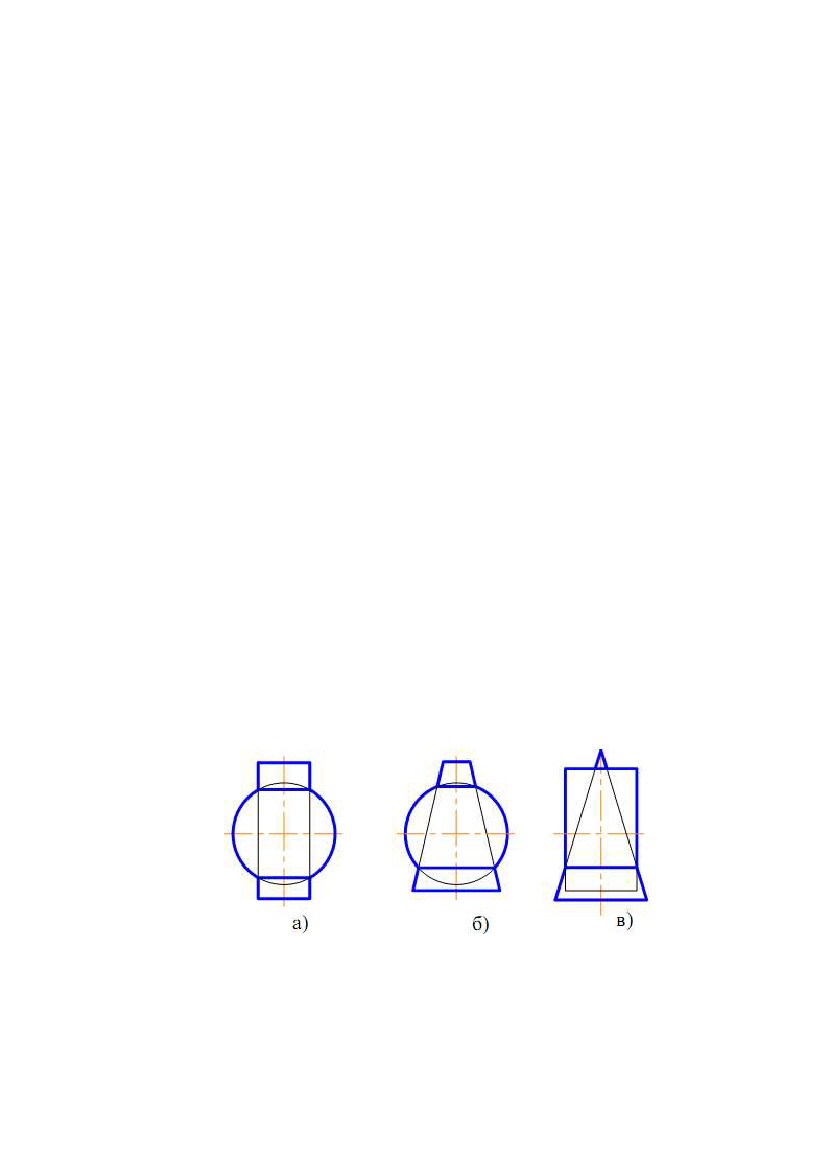
На рис. 8.14,а,б показаний перетин сфери циліндричною і конічною
поверхнями обертання, відповідно. На рис. 8.14,в наведені пересічні співвісні
циліндрична й конічна поверхні обертання.
Рис.8.14
Розглянемо застосування допоміжних концентричних сфер - сфер з
постійним центром. Цей спосіб застосовують при виконанні наступних умов:
а) пересічні поверхні повинні бути поверхнями обертання;
б) осі цих поверхонь повинні перетинатися; точку їхнього перетину
приймають за центр допоміжних сфер;
93
 в) площина симетрії поверхонь повинна бути паралельна до якої- в) площина симетрії поверхонь повинна бути паралельна до якої-
небудь площини проекцій (у протилежному разі застосовують
перетворення креслення).
Розглянемо побудову лінії перетину конічних поверхонь обертання.
На рис. 8.15 показане наочне
зображення, а на рис. 8.16 - комплексне
креслення цих поверхонь. Поверхні і
їхнєрозташуваннязадовольняють
наведеним вище умовам. Перш ніж
будувати проміжні точки, необхідно
знайти опорні точки лінії перетину.
Точки А, В, K і L, а також E, F, С і D –
цеточки,приналежніконтурам
поверхонь. Їх можна знайти способом
концентричних сфер або за допомогою
площин посередників Σ(Σ2) і ∆(∆1).
Розглянемо тепер побудову проміжних
Рис. 8.15
точок на прикладі точок 5 і 6.
Побудови виконаємо на фронтальній площині проекцій. Сфера посередник
Θ(Θ2) із центром у точці О(О2) перетинає конічні поверхні по колах, які на П2
проектуються у відрізки m'( m'2) і n'(n'2) (проекції двох інших кіл не показані).
Точки 52 і 62 їхнього перетину є фронтальними проекціями точок 5 і 6, які
належать лінії перетину поверхонь, тому що належать кожній із цих поверхонь.
Горизонтальні проекції точок 5 і 6 знаходимо з умови приналежності точки
поверхні. У цьому випадку використовується приналежність точок до кола mi
на «вертикальній» конічній поверхні. Точки 51 і 61 визначають по лінії
проекційного зв'язку на mi (mi1).
Аналогічно можна побудувати будь-яку кількість точок шуканої лінії
перетину. Однак слід мати на увазі, що не всі сфери можуть бути використані
для рішення задачі. Розглянемо граничні межі допоміжних сфер. Радіус сфер
посередників змінюється в діапазоні Rmax ≥ R ≥ Rmin, де Rmin – мінімальний
радіус сфери, Rmax – максимальний радіус сфери.
Сфера мінімального радіуса Rmin – це сфера, що торкається однієї
поверхні і перетинає іншу (або теж торкається). На рис. 8.16 така сфера
торкається «вертикальної» конічної поверхні. За допомогою сфери
мінімального радіуса побудовані точки 12=22 і 32=42. Горизонтальні проекції
точок 1, 2, 3 і 4 побудовані аналогічно точкам 5 і 6.
Радіус максимальної сфери дорівнює відстані від точки перетину осей
поверхонь до самої віддаленої точки перетину контурних твірних цих
поверхонь. На рис 8.16 – Rmax =|O2L2|.
Для встановлення видимості проекцій лінії перетину аналізуємо
розташування точок щодо контурів поверхонь. Так, відносно П1, видимою буде
ділянка кривої, розташована вище контуру горизонтальної конічної поверхні
(друга поверхня на видимість на П1 не впливає). Горизонтальна проекція
невидимої частини лінії показана штриховою лінією.
94
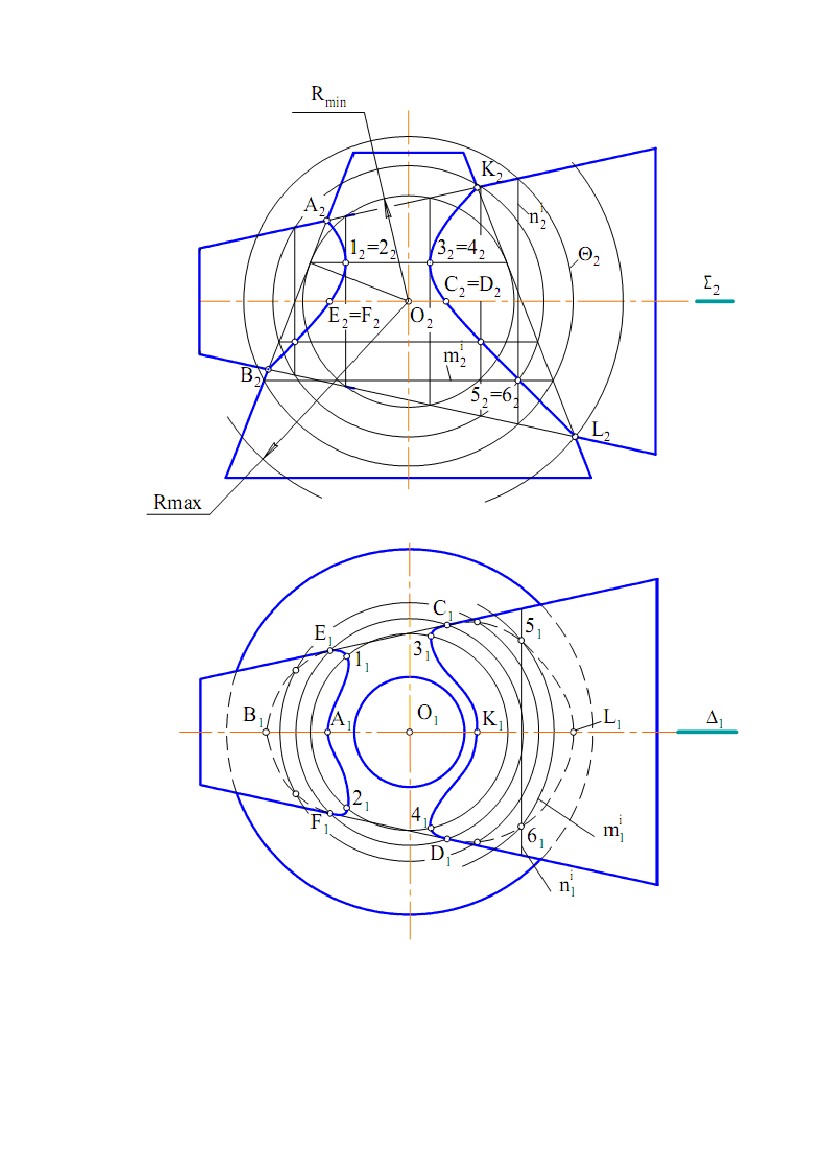 Рис.8.16 Рис.8.16
Точки А, В і K, L належать фронтальним контурам поверхонь і
відокремлюють видиму частину лінії перетину від невидимої при проектуванні
на П2. Фронтальні проекції видимої і невидимої частин лінії перетину на рис.
8.16 збігаються.
95
 4.3. Спосіб ексцентричних сфер 4.3. Спосіб ексцентричних сфер
Спосіб ексцентричних сфер застосовують за умови, якщо:
1) одна з поверхонь - поверхня обертання, а інша - циклічна (має сімейство
кіл);
2) поверхні мають спільну площину симетрії;
3) спільна площина симетрії паралельна площині проекцій (у
протилежному разі варто застосувати перетворення креслення).
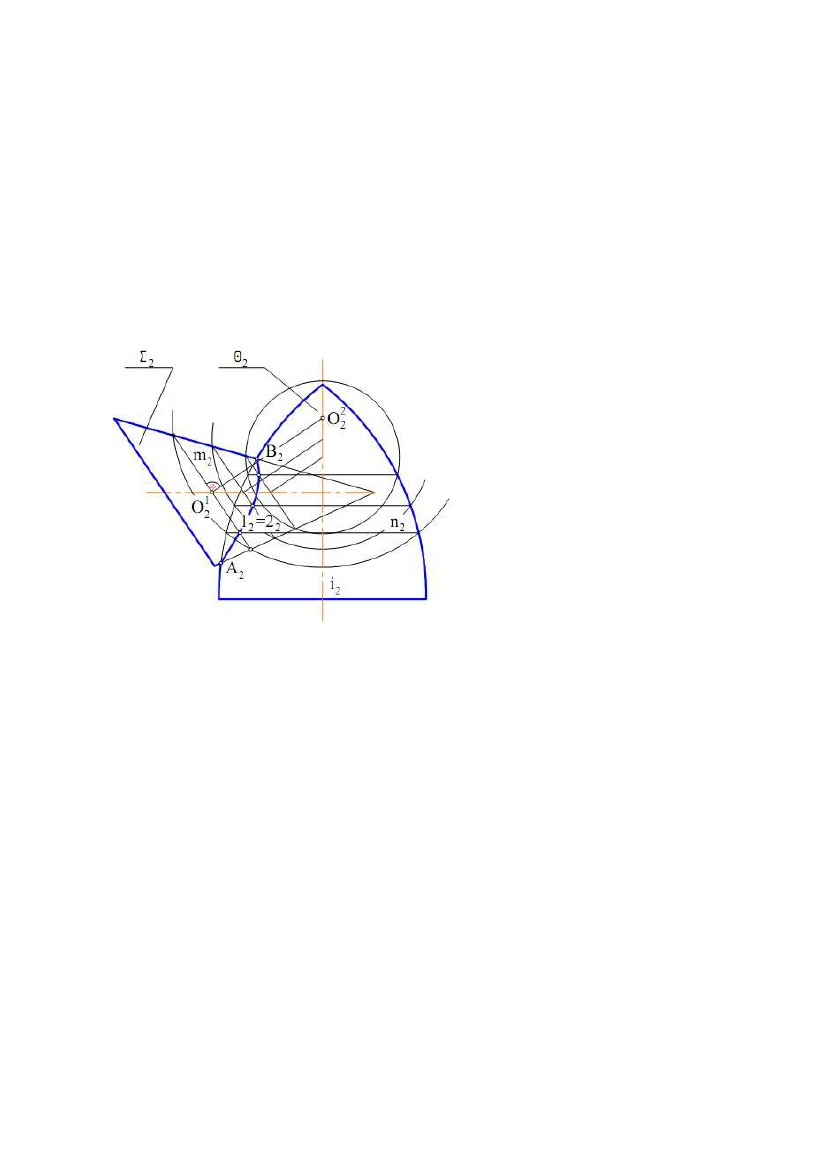
Приклад 1. Побудувати фронтальну проекцію лінії перетину поверхонь
Σ і Θ, спільна площина симетрії яких паралельна П2 (рис. 8.17).
Вирішення. Задані поверхні і
їхнєрозташування
задовольняютьумовам
застосовностіспособу
ексцентричних сфер, що і
використаємо для вирішення
поставленої задачі. Опорними
точками є точки Α(А2) і Β(В2),
розташованівперетині
нарисових твірних. Побудову
проміжних точок виконуємо в
такій послідовності:
1) проводимо на конічній
поверхні коло, яке розташоване в
площині, паралельній її основі іРис. 8.17
на Π2 проектується у відрізок –
m(m2);
2) проводимо перпендикуляр до площини кола m через його центр O1 і
знаходимо центр O2 сфери-посередника;
3) проводимо проекції сфери з центром у точці O2 за допомогою крайніх
точок кола m(m2);
4) будуємо коло n(n2), по якій сфера перетинає поверхню обертання Θ;
5) визначаємо точки 12=22 перетину побудованих кіл.
Проекції інших точок лінії перетину визначаємо аналогічно.
На П2 проекції видимої і невидимої ділянок лінії перетину збіжаться.
Примітка. Запропонуйте вирішення цієї задачі, використовуючи друге
сімейство кіл на еліптичному конусі (див. п.5).
Приклад 2. Побудувати проекції лінії перетину тора і конічної поверхні
обертання (рис. 8.18).
Вирішення. Вихідні поверхні і їхнє розташування задовольняють умовам
застосовності способу концентричних і ексцентричних сфер. Проміжні точки 1,
2, 3 і 4 побудовані способом концентричних сфер, а точки 5 і 6 – способом
ексцентричних сфер.
96
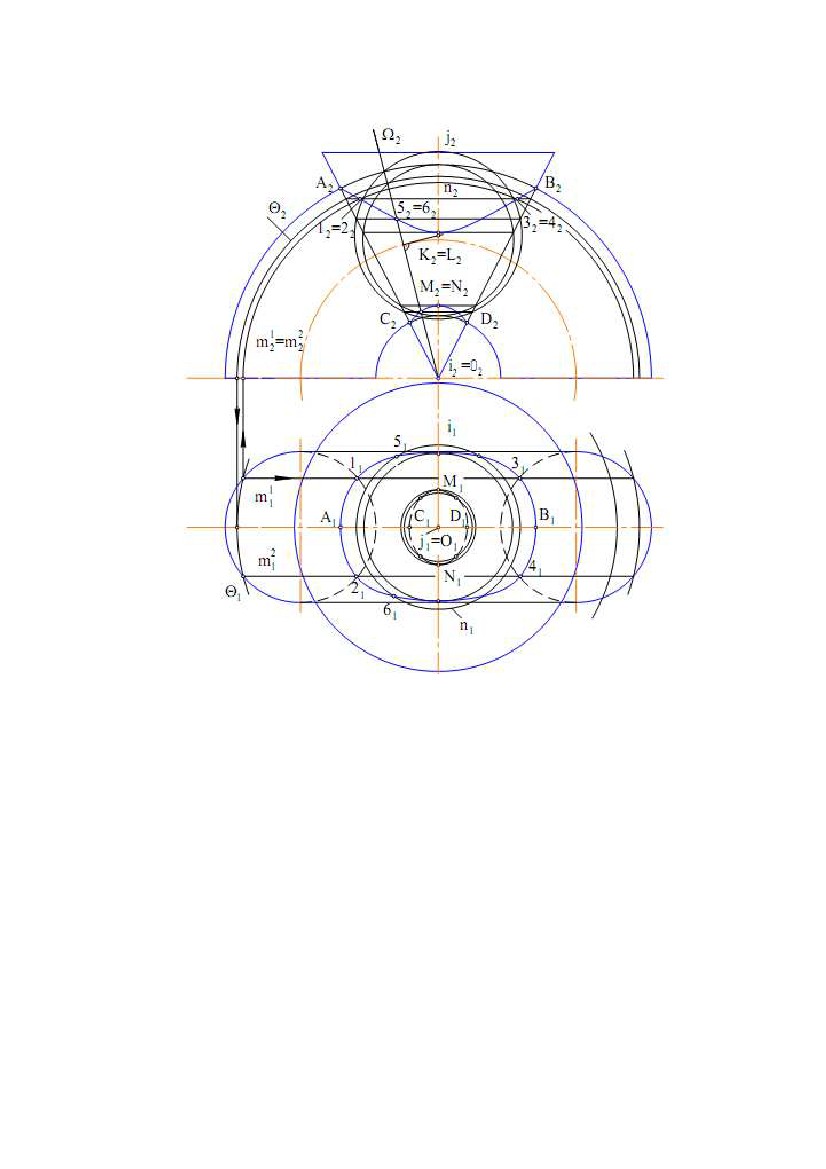 Точки 5 і 6 побудовані за алгоритмом, наведеним у прикладі 1. Коло на торі Точки 5 і 6 побудовані за алгоритмом, наведеним у прикладі 1. Коло на торі
виділено введенням фронтально проектуючої площини ( 2).
Рис. 8.18
Точки 1, 2, 3, 4 побудовані в такій послідовності:
1) побудовані проекції сфери Θ(Θ1, Θ2) із центром у точці О(О1,О2);
2) визначені проекції кола n(n1,n2), по якому сфера перетинає конічну
поверхню;
3) побудовані проекції кіл m1 і m2, по яких сфера перетинає тор; спочатку
побудовані m11 і m12, а потім m21 і m22 (показано стрілками);
4) перетин проекцій кіл m і n задає проекції точок 1, 2, 3, 4.
Точки A, B, C, D, а також K, L, M, N є опорними. Перші розташовані в
перетині нарисових твірних поверхонь, а другі - на сфері мінімального радіуса
(екстремальні).
4.4. Перетин поверхонь другого порядку
У загальному випадку дві поверхні другого порядку перетинаються по
просторовій кривій четвертого порядку. Слід зазначити, що при деяких
97
 особливих положеннях відносно одна одної поверхні другого порядку можуть особливих положеннях відносно одна одної поверхні другого порядку можуть
перетинатися по плоских кривих другого порядку, тобто просторова крива
перетину розпадається на дві плоскі криві. Умови розпадання кривої четвертого
порядку на дві криві другого порядку формулюють у вигляді наступних теорем.
Теорема 1. Якщо дві поверхні
другого порядку перетинаються
по одній плоскій кривій, то вони
перетинаються ще по одній
плоскій кривій. Ілюстрацією цієї
теореми є рис. 8.19 на якому
показані фронтальні проекції сфери
іеліптичногоконуса,що
перетинаються по двох колах –
m(m2) і n(n2). Коло m паралельне
основі (площини кола) конічної
поверхні, а коло n побудоване
відповідно до теореми 1.
Рис. 8.19
Теорема 2 (теорема про подвійний дотик). Якщо дві поверхні другого
порядку мають дотик у двох точках, то лінія їхнього взаємного перетину
розпадається на дві плоскі криві другого порядку.
Площини цих кривих пройдуть
через пряму, що з'єднує точки
дотику. На рис. 8.20 показана
побудова лінії перетину конічної
поверхні обертання і еліптичного
циліндра(осіповерхонь
перетинаються і паралельні П2).
Лінії перетину − еліпси – лежать у
фронтальнопроектуючих
площинах, які проходять через
пряму АВ, що з'єднує точки дотику
А і В, а також точки 1, 2 і 3, 4 (точки
перетину нарисів поверхонь).
Теорема 3 (теорема Монжа).
Якщо дві поверхні другого
порядку описані навколо третьої
поверхні другого порядку або
вписані в неї, то лінія їхнього
взаємного перетину розпадається
на дві плоскі криві. Площини цих
кривих пройдуть через пряму, що
з'єднує точки перетину лінії дотику.
Рис. 8.20
Ця теорема є окремим випадком
98
 теореми 2. Якщо осі пересічних поверхонь обертання паралельні до якої-небудь теореми 2. Якщо осі пересічних поверхонь обертання паралельні до якої-небудь
площини проекцій, то на цю площину криві лінії проектуються у відрізки
прямих.
На рис. 8.21 наведено приклад
побудови лінії перетину двох
конічних поверхонь обертання, осі
яких перетинаються і паралельні
П2. Вихідні поверхні описані
навколо сфери і мають із ними
дотик по колах t(t2) і k(k2). Ці кола
перетинаються в точках 1 і 2.
Площини ліній перетину проходять
через пряму 12 і точки перетину
нарисів поверхонь А, D, В і С.
Рис. 8.21
99
ЛЕКЦІЯ № 9. РОЗГОРТКИ ПОВЕРХОНЬ. АКСОНОМЕТРИЧНІ
ПРОЕКЦІЇ
1. РОЗГОРТКИ ПОВЕРХОНЬ
Визначення. Якщо поверхню, що представляється у вигляді тонкої,
гнучкої і нерозтяжної плівки, можна шляхом згинання сумістити з площиною
без розривів і складок, то поверхня, що володіє цією властивістю, називається
розгортною, а фігура, отримана в результаті суміщення поверхні з площиною,
називається розгорткою.
У математиці доведено, що до розгортних відносяться тільки три групи
лінійчатих поверхонь: конічні, циліндричні й торсові (поверхні дотичні до
просторової кривої). У цих поверхонь уздовж кожної прямолінійної твірної
існує єдина дотична площина, в інших лінійчатих поверхонь уздовж твірної
прямої існує нескінченна множина таких площин. Суміщення поверхні з
площиною приводить до відповідності, установлюваній між множиною точок
поверхні і множиною точок її розгорнення. Ця відповідність має такі
властивості:
1) точці поверхні відповідає єдина точка розгорнення і навпаки;
2) довжини відповідних ліній поверхні і її розгортки рівні;
3) кути, утворені лініями на поверхні, дорівнюють кутам, утвореним
відповідними лініями на розгортці;
4) площі відповідних фігур на поверхні і на розгортці рівні.
З наведених властивостей випливають такі наслідки:
1) пряма лінія поверхні перетвориться в пряму лінію на розгортці;
2) паралельні лінії поверхні перетворяться в паралельні прямі її
розгортки.
Для лінійчатих поверхонь, що розгортаються, будують графічно
наближені розгортки, оскільки в процесі побудови розгорток ці поверхні
заміняються (апроксимуються) уписаними або описаними многогранними
поверхнями. Точні розгортки апроксимуючих многогранних поверхонь
приймають за наближені розгортки поверхонь, що розгортаються. Для
поверхонь, які є нерозгортними, будують умовні розгортки за наступною
схемою:
НП ⇒РП (ГП
ТР, де НП - поверхня нерозгортна, РП – поверхня
розгортна, ГП - гранна поверхня, ТР - точне розгорнення,⇒ - етап апроксимації
⇒
попередньої поверхні наступною. Оскільки в результаті послідовних
апроксимацій вихідна поверхня заміняється гранною, то розглянемо спочатку
побудови точних розгорток гранних поверхонь.
100
|
|
|
 Скачать 5.98 Mb.
Скачать 5.98 Mb.