Курс лекцій НАРИСНА ГЕОМЕТРІЯ. Курс лекцій удк 514. 18 В.І. Лусь. Нарисна геометрія Курс лекцій. Харків хнамг, 2008. 127 с
 Скачать 5.98 Mb.
|
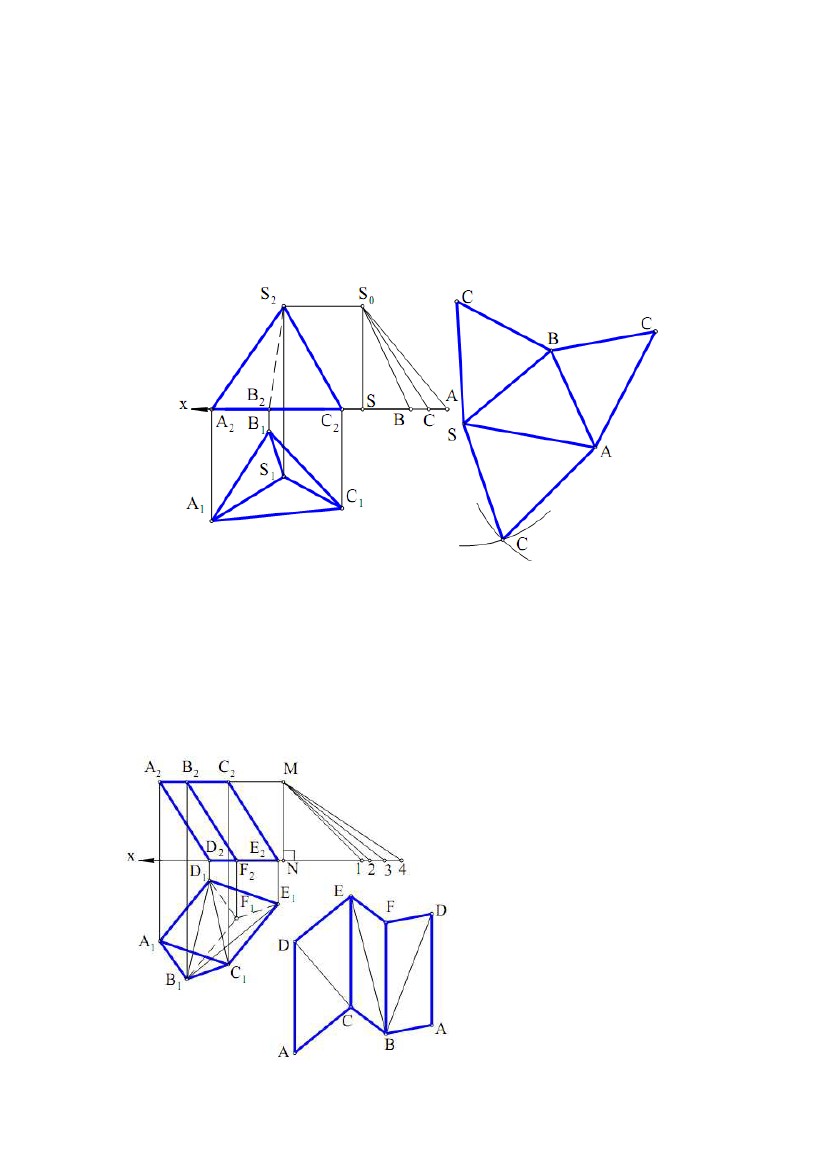 1.1 Розгортки гранних поверхоньВизначення. Розгорткою гранної поверхні називається множина з'єднаних у площині многокутників, конгруентних (рівних) відповідно до її граней. Під з'єднанням розуміється послідовне розміщення многокутників розгортки, що відповідає послідовному розташуванню граней поверхні. Задача. Дано піраміду SABC (рис. 9.1). Побудувати розгортку її поверхні. Рис. 9.1 Основа ABC піраміди належить площині проекцій П1, тому ∆A1B1C1 – його НВ. Для визначення НВ бічних ребер піраміди скористаємося методом прямокутного трикутника (див. рис. 5.1). SS0 ⊥х – загальна різниця висот кінців ребер даної піраміди. Відкладаючи від точки S по осі Х відрізки SB = S1B1, SC = S1C1, SA = S1A1, одержуємо S0В, S0С, S0А – НВ ребер піраміди. Потім осторонь, використовуючи відомі правила побудови трикутника по його сторонах, виконуємо власне побудову розгортки піраміди. Задача. Дано тригранну призму ABCDFE (рис. 9.2). Побудувати розгортку її бічної поверхні. Основи ABC і DFE даноїпризмипаралельні площині проекцій П1 і, отже, проектуються на цю площину у НВ. Кожну з бічних граней призми представляємо у вигляді двох трикутників, розділивши грань діагоналлю. За методом прямокутноготрикутника визначаємо НВ трьох діагоналей BD, BE і CD і одного ребра (ребра за умовою задачі рівні). Рис. 9.2 101  У підсумку на діаграмі натуральних величин відрізків одержуємо:MN – загальна різниця висот ребер; N1 = A1D1 = B1F1 = C1E1; N2 = D1C1, N3 = B1D1, N4 = B1E1; M1 – НВ ребра, М2 – НВ діагоналі DC, М3 – НВ діагоналі BD і М4 – НВ діагоналі ВЕ. Маючи НВ ребер призми, трьох її діагоналей і сторін трикутників основ, будуємо розгортку бічної поверхні як сукупності трикутників, що вибудовуються по їхніх сторонах. Метод, яким були побудовані розгортки в розглянутих двох задачах, називається методом трикутників (метод триангуляції). Метод заснований на можливості побудови єдиного (за формою) трикутника по його заданих сторонах. Замітимо, що чотири, п'ять, відрізків визначають нескінченну множину чотирьох, п'яти, трикутників. Метод трикутників найбільш простий і універсальний при побудові точних розгорток гранних поверхонь, а також наближених і умовних розгорток лінійчатих поверхонь. Розглянемо спеціальні методи побудови розгорток гранних поверхонь. Задача. Дано тригранну призму АВСА1У1С1 (рис. 9.3). Побудувати розгортку призми. Рис. 9.3 Для побудови розгортки застосуємо метод нормального перетину. Метод застосуємо для призматичних поверхонь, в яких бічні ребра являють собою лінії рівня. Послідовність побудов у методі нормального перетину наступна: 1) призма перетинається площиною ∆перпендикулярно до її ребер; 2) визначаються НВ сторін многокутника, по яких площина ∆перетинає поверхню призми; 3) многокутник як ламана лінія розгортається у відрізок прямої, всередині якого відзначаються точки, що відповідають вершинам многокутника; 4) через ці точки проводяться прямі, перпендикулярні до відрізка - розгортки многокутника; 102 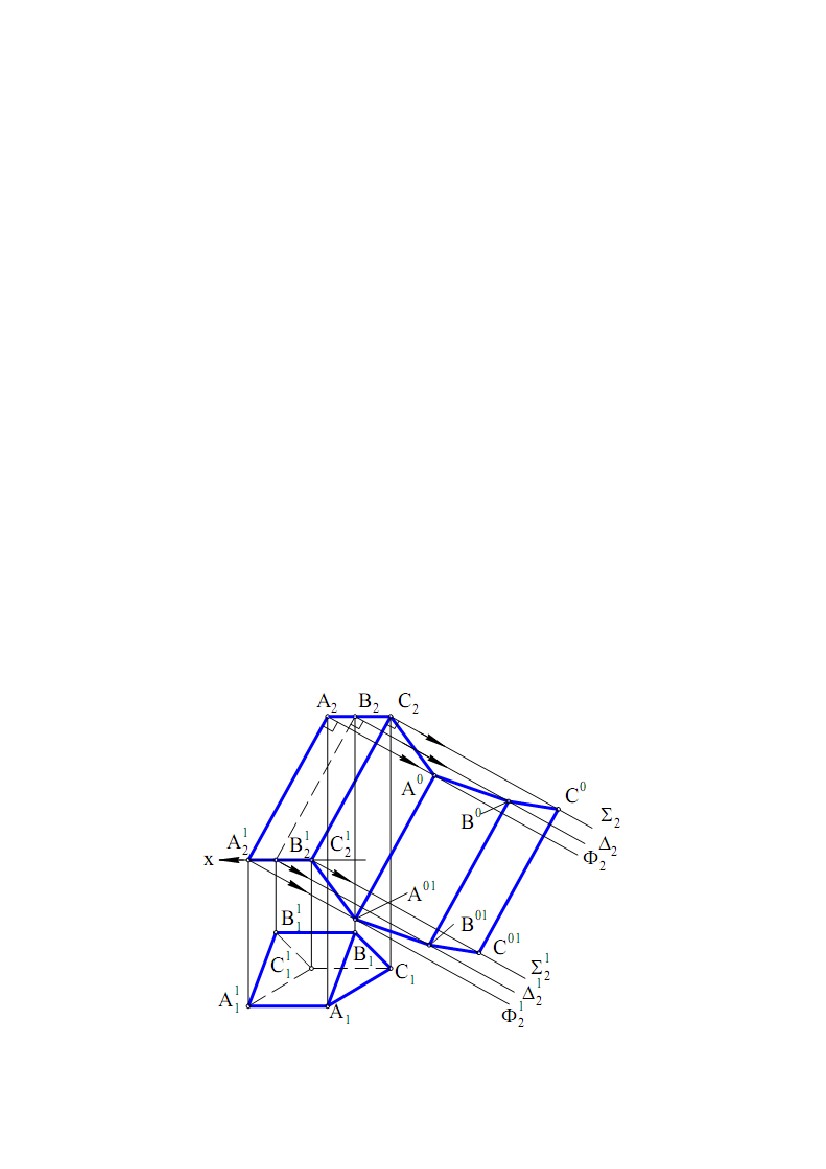 5) на перпендикулярних прямих від зазначених точок відкладаються відрізки,що представляють НВ відповідних відрізків ребер піраміди; 6) кінці відрізків ребер послідовно з'єднуються відрізками прямих ліній; 7) до побудованої розгортки бічної поверхні добудовуються НВ многокутників - основи призми. Застосуємо викладену послідовність до нашої задачі. Оскільки ребра призми АА1, ВВ1, СС1 за умовою задачі є горизонталями, те А1А11,В1В11, З1С11 є НВ цих ребер. Перетнемо бічну поверхню призми площиною ∆, перпендикулярною до її ребер. Оскільки ребра є горизонталями, то ∆⊥П1 і ∆1 – горизонтальний слід площини ∆. 112131 і 122232 – проекції нормального перетину призми. Проекція ∆ 142434 являє собою НВ нормального перетину, побудовану методом заміни площин проекцій, де х1║∆1. Осторонь від КК, на∆ горизонтальній прямій, послідовно розташовуємо відрізок 13 = 1434, 32 = 3424, 21 = 2414 і проводимо через їхні кінці вертикальні прямі. На цих прямих відкладаємо відрізки: 1В = 11В1, 1В1= 11В11; 3С = 31С1, 3С1= 31С11; 2А = 21А1, 2А1= 21А11. Многокутник ВСАВВ1А1С1У1 являє собою розгортку бічної поверхні заданої призми. Добудувавши до неї ∆АВС і ∆А1С1У1, одержуємо повну розгортку призми. Задача. Дано призму АВСА1С1У1 (рис. 9.4). Побудувати її розгортку. Для цього можна використати відомий метод розкочування. Його застосування можливо для таких призматичних поверхонь, в яких бічні ребра й площини основ є прямими і площинами рівня. Суть методу полягає в послідовному обертанні граней призми навколо її бічних ребер до положення суміщення із площиною, що проходить через одне із ребер і паралельні площини проекцій, тобто кожна грань залишає свій «відбиток» у цій площині. Рис. 9.4 103 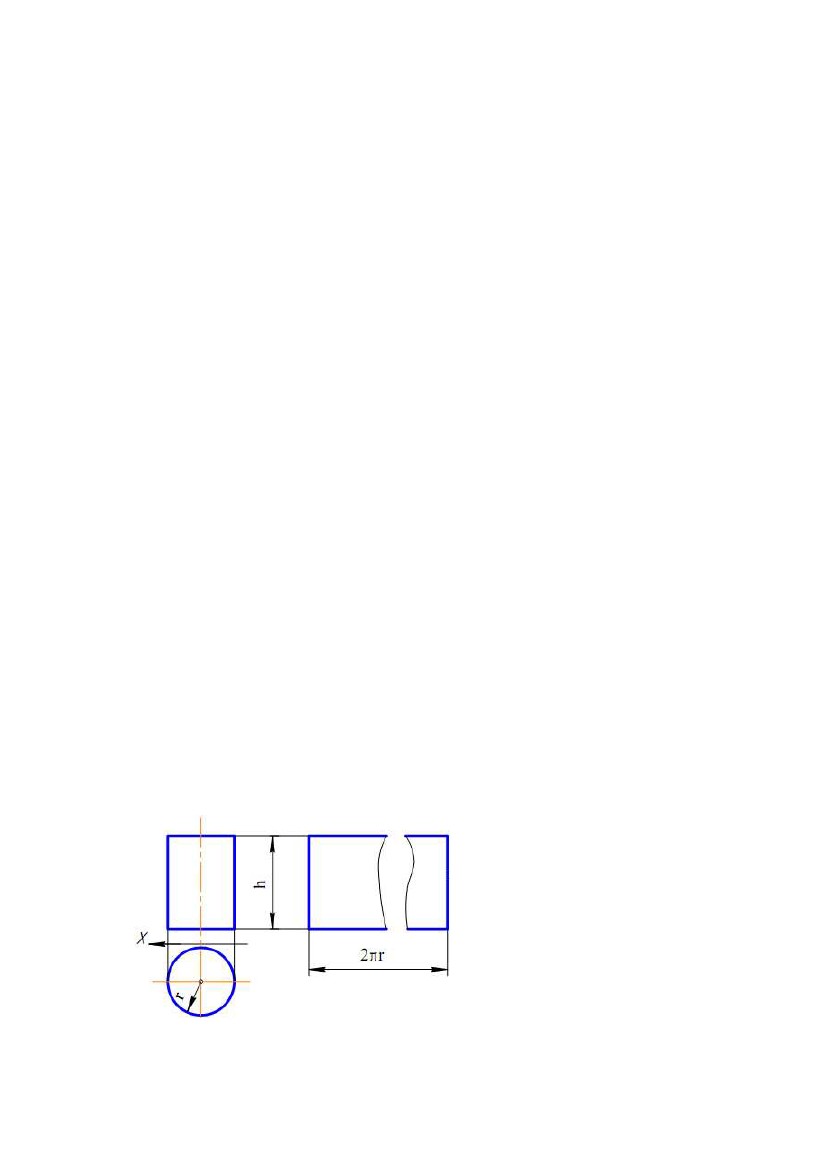 Множина послідовно отриманих і розташованих «відбитків» у площиніявляє собою розгортку бічної поверхні призми. Розглянемо вирішення даної задачі. Бічні ребра призми є фронталями, а площини основ - горизонтальними площинами рівня. Умови задачі відповідають методу розкочування. Нехай перше обертання – обертання грані АСС1А1, відбувається навколо осі СС1. Повернемо цю грань до суміщення із площиною розгортки, що проходить через ребро СС1 і паралельна площині проекцій П2. У цьому випадку вершини А и А1 будуть обертатися в проектуючих площинах, Ф ⊥П2 і Ф1 ⊥П2 відповідно, які перпендикулярні до ребра АА1. Суміщені положення A0 і A01 вершин А и А1 будуть належати фронтальним слідам Ф2 і Ф21 площин Ф и Ф1 відповідно і відстояти від точок З2 і З21 на відстані З2A0 = C21A01= А1С1 = А11С11. Наступним обертанням навколо осі A0A01 домагаємося суміщення грані АВВ1А1 із площиною розгортки. При цьому суміщенні положення B0 і B01 вершин В и В1 відповідно будуть належати фронтальним слідам ∆2 і ∆21 площин ∆⊥П2 і ∆⊥П2 і відстояти від точок A0 і A01 на відстані B0A0= B01A01= В1А1 = В11А11. Останнє, третє обертання, буде відбуватися навколо осі B0B01 і дозволить одержати суміщення грані ВСС1В1 із площиною розгортки, при цьому суміщені положення C0 і C01 вершин С и С1 будуть належати фронтальним слідам Σ2 і Σ21 проектуючих площин ⊥П2 і Σ1 ⊥П2 і відстояти від точок B0 і B01 на відстані C0B0= C01B01= С1В1 = С11В11. Отриманий у підсумку побудов многокутник С2A0B0C0C01B01A01С21 буде являти собою розгортку бічної поверхні заданої призми. 1.2. Наближені розгортки поверхонь Побудову наближених розгорток виконують в наступній послідовності: 1) задану лінійчату поверхню, що розгортається, заміняють (апроксимують) гранною поверхнею; 2) будують точну розгортку гранної поверхні; 3)точнурозгортку приймаютьзанаближену розгортку заданої поверхні. Длядеякихлінійчатих поверхонь, що розгортаються, немає необхідності в їхній заміні гранними поверхнями. Так,відсік циліндричної поверхні обертання радіуса r і висотою h має розгорткою Рис. 9.5 прямокутник зі сторонами h і 2πr (рис. 9.5). 104 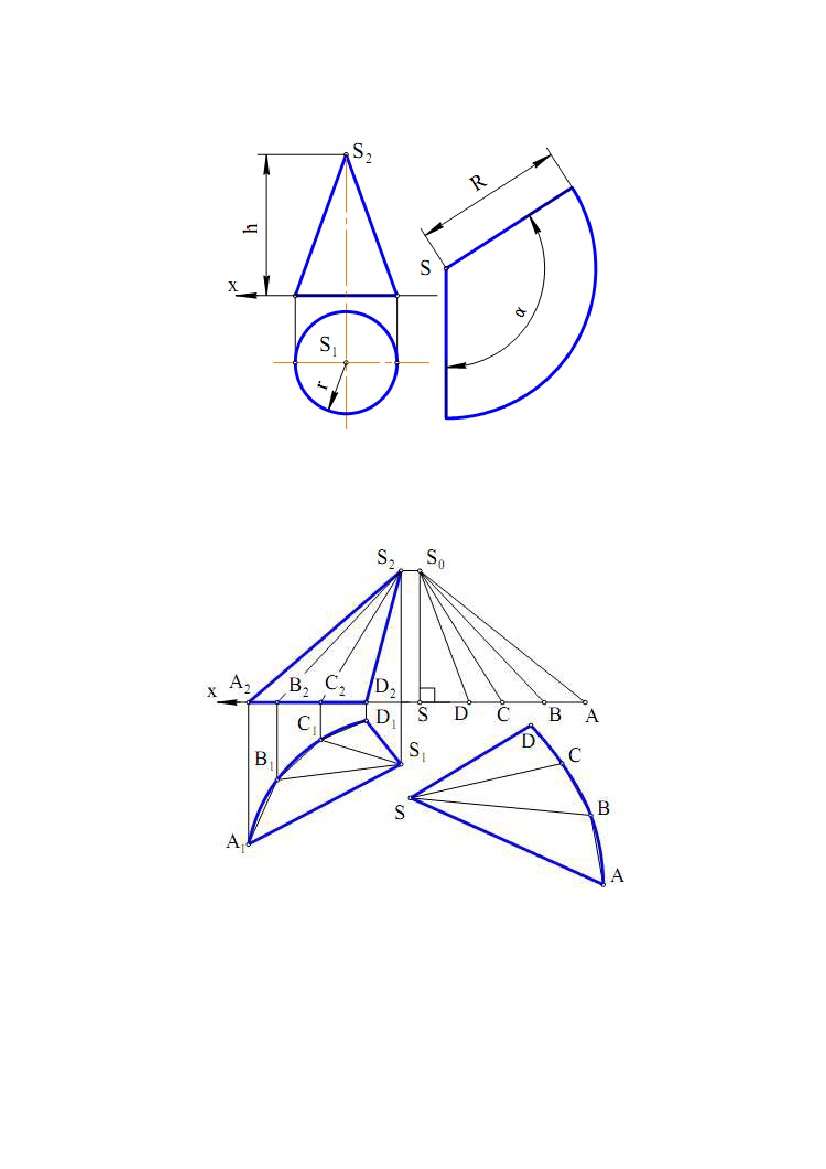 Розгорткою конічної поверхні обертання висотою h і основою радіуса r єсектор радіуса R = √ h2 + r2 з кутом α = 2 r/R (рис. 9.6). Рис.9.6 Розглянемо приклад побудови наближених розгорток. Задача. Дано відсік конічної поверхні (рис. 9.7). Побудувати його наближену розгортку. Рис. 9.7 Плоску криву лінію – напрямну конічної поверхні спочатку заміняють уписаною ламаною лінією ABCD(A1B1C1D1, A 2B2C2D2), що за умовою задачі належить площині проекцій П1 і тому A1B1C1D1 – її НВ. Потім з'єднують вершини ламаної з вершиною S конічної поверхні й одержують уписану пірамідальну поверхню SABCD, яка заміняє дану конічну поверхню. Використовуючи метод прямокутного трикутника, будують діаграму НВ ребер 105  уписаної пірамідальної поверхні. При цьому SS0 – загальна різниця висот кінцівребер піраміди; SD = S1D1, SC = S1C1, SB = S1B1, SA = S1A1; S0D, S0C, S0B, S0A – являють собою НВ ребер піраміди. SDCBA – розгортка бічної поверхні заданого конічного відсіку. Задача. Дано відсік поверхні еліптичного циліндра (рис. 9.8). Побудувати розгортку його бічної поверхні. Впишемо в дану поверхню деякупризматичну поверхню,розділивши напрямну лінію циліндра - коло, на рівне число частин, наприклад на 12 (на рис. 9.8 внаслідоксиметричності заданоїповерхні,для простотипобудови виконане ділення половини поверхні на 6 частин). Бічніребравписаної призми є фронталями, а її основи – многокутники належать горизонтальним площинам рівня. Із цієї причинибічніребра проектуються на П2 у НВ, а многокутники основ – у НВ на П1. Відзначені умови задачі відповідають методу Рис. 9.8 розкочування для побудови розгортки вписаної призми. Оскільки призма має площину симетрії, що проходить через лінію центрів твірний еліптичний циліндр кіл і яка є фронтальною площиною рівня, то для скорочення побудов виконаємо побудову розгортки тільки половини призми. Обертання призми по методу розкочування варто починати з ребра КК1(К1К11, К2К21). Тому площиною розгортки призми буде фронтальна площина рівня, що проходить через ребро КК1. Послідовним обертанням навколо ребер призми домагаємося сполучення всіх її граней із площиною розгортки. При цьому К2F = K21F1= K11F11= K1F1; FE = F1E1= F11E11= F1E1 і т.д. Отриманий многокутник ABCD…D1C1B1A1являє собою точну розгортку половини бічної поверхні вписаної призми, що, у свою чергу, визначає наближену розгортку відповідної половини поверхні еліптичного циліндра. Задача. Дано відсік торсової поверхні (рис. 9.9). Побудувати його розгортку. Торсова поверхня – це лінійчата поверхня, що розгортається, утворена дотичними прямими до просторової кривої, яка має назву ребра повернення цієї 106 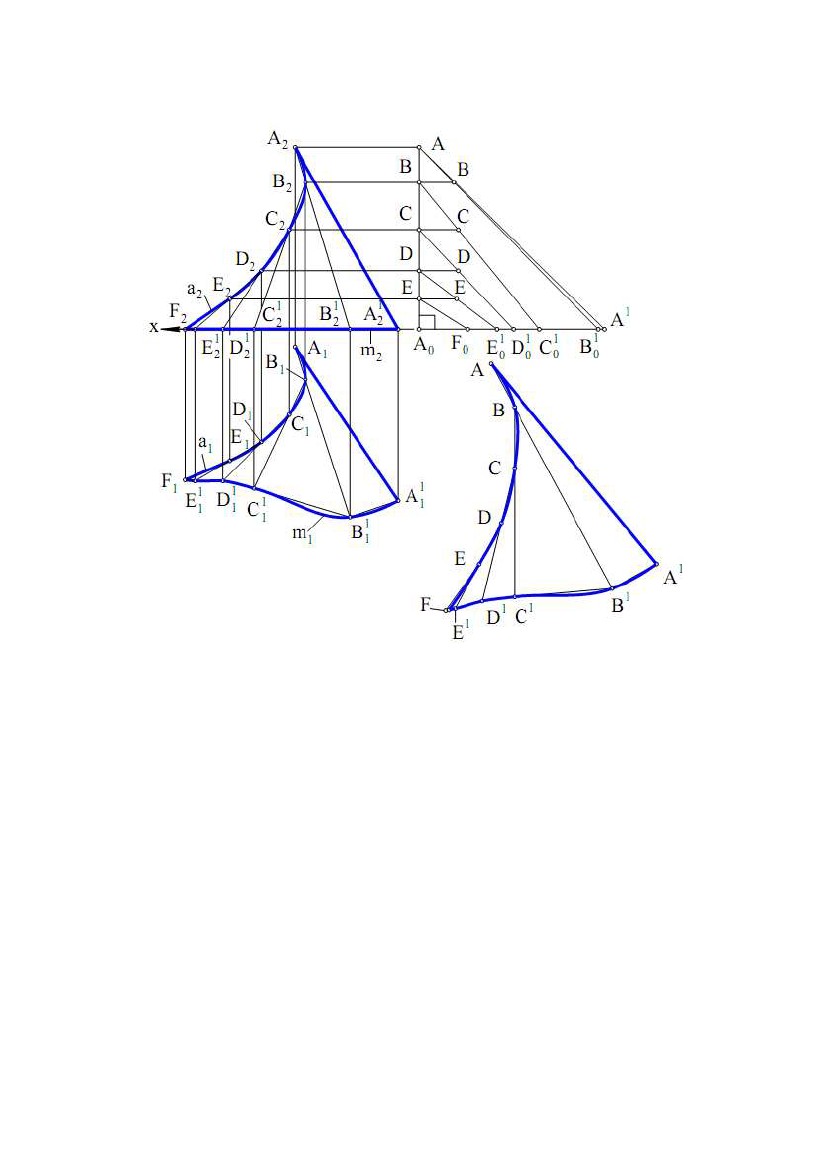 поверхні. У нашій задачі відсік заданої поверхні обмежений ребром поверненняа(а1, а2), плоскої кривої m(m1, m2) і відрізком АА1 її твірної. Рис.9.9 Замінимо криву m вписаною ламаною лінією A1B1C1D1E1F із проекціями A11B11C11D11E11F1 і A21B21C21D21E21F2. Потім виконаємо наступні дії: 1) з'єднаємо точки А и В1для одержання відрізка АВ1(А1В11, А2В21); 2) відзначивши точку перетину АВ1 ∩ а = В(В1, В2), з'єднаємо точки В и С1 для одержання відрізка ВС1(В1С11, В2С21); 3) відзначивши точку перетину ВР1∩ а = С(С1, С2), з'єднаємо точки С и D1 для одержання відрізка СD1(С1D11, C2D21); 4) відзначивши точку перетину СD1∩ а = D(D1, D2), з'єднаємо точки D і Е1 для одержання відрізка DЕ1(D1Е11, D2Е21); 5) відзначивши точку перетину DЕ1∩ а = Е(Е1, Е2), з'єднаємо точки Е и F1 для одержання відрізка EF(E1F1, E2F2). У підсумку виконання побудов одержимо вписаний у ребро повернення а просторовий многокутник ABCDEF(A1B1C1D1E1F1, A2B2C2D2E2F2) і вписану в торсову поверхню гранну поверхню з ребрами АА1, АВ1, ВР1,СD1, DE1, EF. Очевидно, гранями вписаної в торсову поверхню гранної поверхні є трикутники, в яких дві вершини є вершинами плоскої ламаної лінії, вписаної в лінію m, а третя вершина – це вершина просторової ламаної, вписаної в ребро повернення а. Сторона одного з двох сусідніх трикутників належить стороні 107  іншого і служить ребром гранної поверхні. Подальші побудови полягають увизначенні НВ двох із трьох сторін кожного трикутника методом прямокутного трикутника, оскільки третя сторона спроектована на П1 у НВ. Для цього будується діаграма НВ сторін трикутників – граней. При цьому на прямій АА0 від точки А0 відкладаються різниці висот кінців відрізків – сторін трикутників, а по осі Х від точки А0 – довжини горизонтальних проекцій цих сторін. Причому А0F0 = E1F1, А0E01= D1E11, А0D01= C1D11, А0C01= B1C11,А0В01= А1В11, А0A1= А1A11. Потім виконуються послідовні побудови трикутників – граней по трьох їхніх сторонах, що приводить до плоскої області, обмеженої лінією ABCD…D1C1B1A1... Ця плоска область буде наближеною розгорткою заданої торсової поверхні. 1.3. Умовні розгорнення поверхонь, що не розгортаються Розглянемо кілька прикладів, виходячи із зазначеної раніше схеми побудови умовної розгортки поверхні. Задача. Дано поверхню обертання (рис. 9.10). Побудувати її розгортку. Очевидно, дана поверхня не є тією, що розгортається і для неї можна побудувати лише умовну розгортку. Розділимо поверхню обертання осьовими площинами ∆i, де i = 1, 2, 3, …, на рівне число частин (відсіків) і виберемо одну з них (наприклад, шосту частину), обмежену проектуючими площинами ∆1 і ∆2, що мають горизонтальні сліди ∆11 і ∆21. Приймемо нарисову лінію t(t1, t2) за напрямну лінію циліндричної поверхні з відрізками її фронтально - проектуючих твірних між площинами ∆1 і ∆2. Рис.9.10 Відсіком цієї поверхні виконана апроксимація обраної частини вихідної поверхні. Відповідно до схеми побудови умовної розгортки виконаємо другу 108  апроксимацію, замінивши відсік циліндричної поверхні відсіком призматичноїповерхні. Для цього виберемо на напрямній t ряд точок, наприклад S, 1, 2, 3, 4, 5, і проведемо через них фронтально проектуючі твірні, наприклад, АВ ∋5. Відрізки цих прямолінійних твірних між осьовими площинами ∆1 і ∆2 заміняють відповідні відрізки паралелей (кіл) вихідної поверхні і є ребрами призматичної поверхні, а ламана лінія S12345, вписана в лінію t, є напрямною лінією цієї поверхні. Точна розгортка призматичної поверхні, вписаної в циліндричну поверхню, служитиме наближеною розгорткою описаної циліндричної поверхні й умовною розгорткою відсіку вихідної поверхні обертання. Для побудови розгортки відсіку вписаної призматичної поверхні проведемо осторонь від вихідного КК горизонтальну лінію й виберемо на ній точку 5. По обидві сторони від точки 5 відзначимо горизонтально й симетрично точки А і В такі, що АВ = А1В1. Вертикально від точки А відкладемо відрізок 54 = 5242. Потім від точки 4 горизонтально і симетрично відмітимо точки С і D такі, що CD = C1D1 і т.д. У підсумку побудов одержуємо два ряди точок, симетричних щодо лінії 5S. З'єднавши точки кожного ряду лекальними кривими, одержимо умовну розгортку виділеного відсіку вихідної поверхні. Приєднавши до неї такі ж (рівні) розгортки інших відсіків, одержимо повну умовну розгортку поверхні. Задача. Дано чверть поверхні тора (рис. 9.11). Побудувати її розгортку. Рис.9.11 Для вирішення задачі розсічемо чверть поверхні тора фронтально проектуючими осьовими площинами ∆i, i = 1, 2, 3…на рівні відсіки й виділимо один з них, наприклад, розташований між січними площинами П1 і ∆1. 109  Проведемо площину симетрії ∆ цього відсіку. Вона розсікає відсік тора по колуt ,при цьому t2 = 1272, де t11 – НВ цього кола. Замінимо виділений відсік поверхні чверті тора відсіком описаної циліндричної поверхні з напрямною t і твірними – фронтальними лініями рівня, розташованими між площинами П1 і ∆1. Відрізки цих твірних у межах між П1 і ∆1 заміняють відрізки відповідних паралелей (кіл) поверхні чверті тора. Наприклад відрізок АВ(А2В2) прямої заміняє дугу паралелі 11111(1211211), відрізок CD(C2D2) заміняє дугу паралелі 71711(7217211) і т.д. Після цього замінимо відсік описаної циліндричної поверхні відсіком призматичної поверхні, вписаної в циліндричну. Лінія m (m2) – ламана лінія, вписана в коло t і проходить через вершини 1, 2, 3, 4, 5, 6, 7. Ця лінія служить напрямною вписаної призматичної поверхні й має свою НВ ламану лінію m11, що проходить через вершини 111, 211,…, 711... Твірні АВ, …, CD циліндричної поверхні є ребрами призматичної поверхні. Точна розгортка відсіку вписаної призматичної поверхні є наближеною розгорткою відсіку описаної циліндричної поверхні й умовною розгорткою відсіку поверхні тора. Для побудови умовної розгортки відзначимо осторонь від КК на горизонтальній прямій точку 1 і симетричні точки А і В такі, що АВ = А2В2. На вертикальній прямій на точці 1 відкладемо відрізок 12 = 111211 і проведемо через точку 2 горизонтальну пряму, на якій побудуємо симетричні точки M і N так, що MN = M2N2 і т.д. У підсумку побудов одержимо два вертикально симетричних точкових ряди A, N, …C і B, M,…, D. Відбивши їх симетрично щодо горизонтальної прямої АВ і провівши через кожну з них лекальну криву, одержимо умовну розгортку виділеного відсіку поверхні тора. Додавши до неї такі ж (рівні) розгортки інших відсіків, одержимо повну умовну розгортку чверті поверхні тора або всієї його поверхні. Задача. Дано поверхню обертання з віссю обертання t і твірною кривою m (рис. 9.12). Побудувати її розгортку. Очевидно, дана поверхня може мати тільки умовну розгортку. Для її побудови можна застосувати метод конусів. Вирішення задачі в цьому випадку може бути наступним: 1) заміняємо твірну m ламаною лінією ABCS1(A1 B1 C1 S11, A2 B2 C2 S21); 2) розсікаємо задану поверхню обертання площинами, перпендикулярними осі t і які проходять через вершини ламаної; 3) кола, що утворяться в перетинах, приймаємо як основи конічних поверхонь з вершинами і радіусами основ: S1,r1; S2,r1; S2,r2; S3,r2; S3,r3;Рис. 9.12 4) для кожної конічної поверхні будуємо її точну розгортку на основі раніше наведеної формули αi = 2 πr/ R, де r приймає значення r1, r2, r3; R приймає значення S1C, S2C, S2B, S3B, S3A; α1 = ⋅3S14, α2 = ⋅2S25, α3 = ⋅1 S36. 110 |