Курс лекцій НАРИСНА ГЕОМЕТРІЯ. Курс лекцій удк 514. 18 В.І. Лусь. Нарисна геометрія Курс лекцій. Харків хнамг, 2008. 127 с

• Название: Курс лекцій удк 514. 18 В.І. Лусь. Нарисна геометрія Курс лекцій. Харків хнамг, 2008. 127 с
• Анкор: Курс лекцій НАРИСНА ГЕОМЕТРІЯ.doc
• Дата: 09.05.2018
• Размер: 5.98 Mb.
• Имя файла: Курс лекцій НАРИСНА ГЕОМЕТРІЯ.doc
• Тип: Курс лекцій; #19052
• страница: 12 из 13

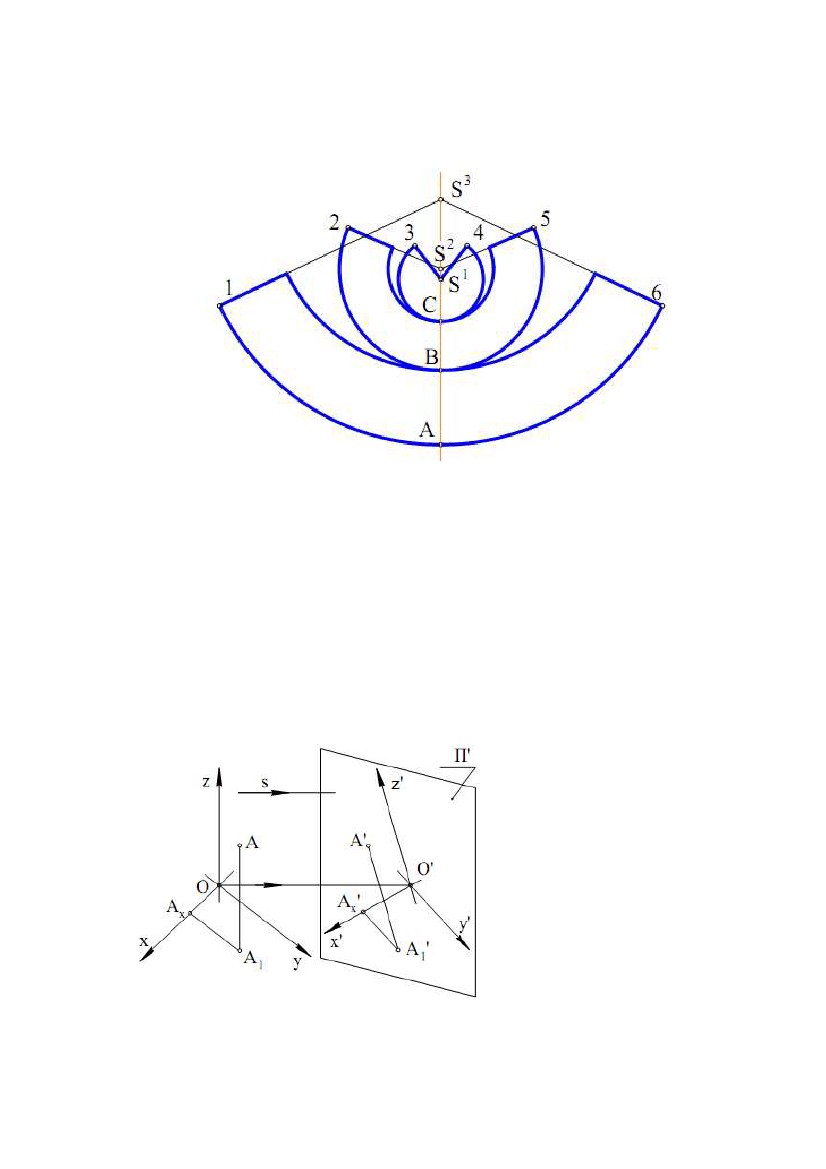У підсумку побудов одержуємо умовну розгортку вихідної поверхні

обертання, складену з трьох точних розгорток таких конічних поверхонь:

повної S1, r1 і двох урізаних поверхонь S2,r1,r2; S3,r2,r3, (рис. 9.13).

Рис.9.13

2. АКСОНОМЕТРИЧНІ ПРОЕКЦІЇ

У перекладі з грецької мови слово «аксонометрія» означає вимір по осях.

Особливістю аксонометричного проектування є те, що разом з фігурою на

площину проектується і просторова система координат, пов'язана із цією

фігурою. При цьому жодна з осей системи координат не проектується в точку.

Використання аксонометричного проектування дозволяє підвищити наочність

зображення фігури.

Розглянемо проекційну схему

одержання аксонометричної

проекції найпростішої фігури

– точки (рис. 9.14).Точка A і

просторовасистема

координат Oxyz зв'язані

координатноїламаної

ОAx1A, ланками якої є

координатні відрізки |OAx| =

|xA|, |Ax1| = |yA|, |A1A|= |zA|.

Площина П' –

аксонометрична площина,

s – напрямок проектування.

Рис. 9.14

Всі проектуючи прямі

паралельні s. Якщо пряма s не перпендикулярна до П', то маємо косокутне

проектування і одержимо косокутну аксонометричну проекцію.

111

Якщо пряма s перпендикулярна П', то маємо ортогональне проектування й

одержимо ортогональну (прямокутну) аксонометричну проекцію. Надалі

розглядається ортогональне проектування і ортогональні аксонометричні

проекції.

На площині П' після проектування одержимо: A' – аксонометрична

проекція точки A; O'x'y'z' – аксонометрична система координат (проекція

системи Oxyz); x', y', z' – аксонометричні осі (проекції осей x, y, z); A1' –

аксонометрична проекція горизонтальної проекції точки A, або вторинна

проекція точки A; O'Ax' A1' A' – аксонометрична координатна ламана (проекція

ламаної OAx1A). Ланки аксонометричної координатної ламаної паралельні

відповідним аксонометричним осям, тому що паралельні прямі проектуються в

паралельні прямі.

Нехай кут між віссю x і віссю x' (проекція x на П') дорівнює α, між y і y'

– β, між z і z' – γ. Якщо відрізок розташований на осі x або на лінії паралельної

осі x, то його кут нахилу до площини П' дорівнює α, якщо – на осі y, то – β,

якщо – на осі z, то – γ. Тоді |O'Ax'| = |OAx|cosα, |Ax'А1'| = AxА1|cosβ, |A1'A'|=

|A1A|cosγ. Введемо наступні позначення: u = cosα; v = cosβ; w = cosγ. Числа u,

v, w називаються коефіцієнтами спотворення по аксонометричних осях x', y',

z' відповідно. Знаючи координати точки A(x; y; z) і коефіцієнти u, v, w, можна

знайти аксонометричні координати точки A' (x';y';z'): x'= xAu; y' = yAv;

y'= yAw. Для коефіцієнтів спотворення справедлива залежність яку приймаємо

без доказу

u2 + v2 + w2 = 2,

(9.1)

Оскільки проекції фігури на паралельні площини рівні, то замість П'

(рис. 9.1) можна взяти будь-яку площину їй паралельну. Для підвищення

наочності ортогональних аксонометричних проекцій позитивні півосі осей x, y,

z розташовують в одному півпросторі щодо аксонометричної площини,

проведеної через початок координат (рис. 9.1, точка O). При цьому кути α, β, γ

будуть більше нуля, але менше дев'яноста градусів. Тоді коефіцієнти u, v, w

(косинуси цих кутів) будуть менші одиниці, але більше нуля.

Якщо відомі коефіцієнти спотворення u, v, w, то легко знайти кути α, β, γ

(α = arcos u, β = arcos v, γ = arcos w). Знаючи коефіцієнти спотворення u, v, w і

визначивши по них кути α, β, γ, можна знайти кути між аксонометричними

осями. Формула (1.1) для розрахунку проекції кута, що при проектуванні

прямого кута (ϕ = 900) на площину П'(ϕ1 = ϕ ') має вигляд:ϕϕ

cosϕ '= – tgα·tgβ.ϕ·

(9.2)

Наприклад, кут між осями x і y дорівнює 90°, тобто (x,y) = 90°, він

проектується на площину П' у кут між осями x' і y'. По формулі (9.2)

cos(x',y')= – tgα·tgβ, де α – кут між x і x', β – кут між y і y'·

112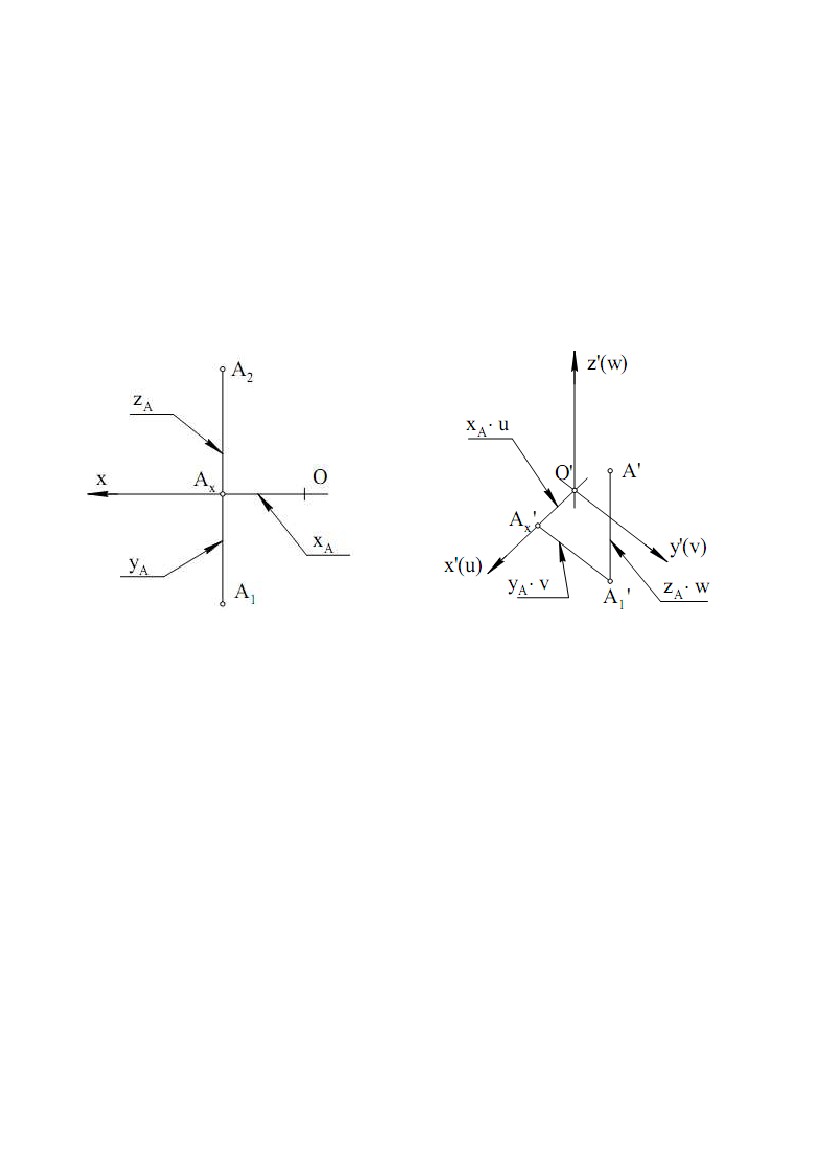

За величиною косинуса знайдемо кут між аксонометричними осями x' і y'.

Аналогічно можна знайти й два інших кути.

Звернемо увагу на те, що кути між аксонометричними осями більше 90°

(тупі), тобто прямі кути між осями проектуються в тупі кути між

аксонометричними осями. Дійсно, у формулі (9.2) тангенси гострих кутів

більше нуля, виходить, косинус проекції кута негативний, тобто проекція кута

більше 90°.

Розглянемо побудову аксонометричної проекції точки A за комплексним

кресленням цієї точки (рис. 9.15). Нехай на аксонометричній площині П' відоме

положення осей x', y', z' і відомі коефіцієнти спотворення по цих осях u, v, w

(рис. 9.16).

Рис.9.15

Рис.9.16

Звернемо увагу на те, що на рис. 9.15 аксонометрична площина є

площиною креслення. Вісь z' завжди розташовується вертикально. Замірявши

на комплексному кресленні відповідні відрізки, знаходимо координати x, y, z.

Помножимокоординатинакоефіцієнтиспотворення,побудуємо

аксонометричну координатну ламану OAx'1'A' і аксонометричну проекцію

точки A – точку A'. Якщо яка - небудь координата менша нуля (негативна), то

аксонометричний координатний відрізок (ланка аксонометричної координатної

ламаної) відкладається в протилежну сторону щодо позитивного напрямку,

зазначеного стрілкою на аксонометричній осі.

2.1. Ортогональна (прямокутна) ізометрична проекція

Ортогональна ізометрична проекція (ізометрія) є ортогональною

аксонометричною проекцією при u = v = w. За формулою (9.1) одержимо u =v =

w = 0,82. За формулою (9.2) визначимо, що кут між будь-якими осями 120°.

113

Побудову ізометрії точки виконуємо так само, як показано на рис. 9.15,

9.16. Кожну координату точки необхідно помножити на 0,82. Така ізометрія

називається точною або теоретичною. Якщо ізометрію точки виконати в

масштабі 1,22:1, то координату точки потрібно помножити на 0,82 (коефіцієнт

спотворення по осі), а потім помножити на 1,22 (збільшення через виконання в

масштабі), тоді ізометрична координата, наприклад, xА' дорівнює 0,82·1,22·xА··

= xА.

Виходить, при виконанні ізометрії в масштабі 1,22:1 (масштаб

приведення) можна координати точки не множити на коефіцієнти спотворення,

а брати їх такими ж, як на комплексному кресленні. Ізометрія, виконана в

масштабі 1,22:1, називається приведеною або практичною, коефіцієнти

спотворення при цьому u = v = w = 1.

На рис. 9.17 показане комплексне креслення куба зі зрізаною вершиною.

На рис. 9.18 побудована його приведена ізометрія. Поруч з ізометрією дана

схема розташування ізометричних осей з вказівкою коефіцієнтів спотворення і

масштабу приведення. На рис. 9.17 в якості системи координат, пов'язаної з

кубом, узята Gtqr, а не система координат Oxyz комплексного креслення, як

на рис. 9.15, 9.16.

Рис. 9.17

Рис. 9.18

Система Gtqr задана своїми проекціями G1t1q1r1 і G2t2q2r2. Тепер ця система

проектується в ізометричну систему координат і щодо неї беруть координати

вершин куба.

Ізометрію куба легко побудувати, якщо побудувати ізометрію його

вершин і з'єднати їх. Побудуйте, як вправу, ізометрію куба, зв'язавши з ним

систему координат комплексного креслення Oxyz, що в цьому випадку буде

проектуватися в ізометричну систему координат.

На рис. 9.19 показане комплексне креслення кривої k, на рис. 9.20

побудована приведена ізометрія цієї кривої.

114

Рис. 9.20Рис. 9.19

Як система координат, пов'язана з кривою, взята система координат

комплексного креслення Oxyz, що проектується в ізометричну систему

координат O'x'y'z'. Для побудови ізометрії кривої необхідно побудувати

ізометрію ряду її точок і з'єднати їх кривою лінією. Так можна побудувати

ізометрію будь-якої кривої, але для побудови ізометрії кола зручно використати

спеціальні методи. Нехай коло діаметром d розташоване в площині Oxy (або в

площині, паралельній Oxy). Це коло проектується на аксонометричну площину

в еліпс. Всі діаметри еліпса, крім одного, будуть менше діаметра кола. Великий

діаметр еліпса дорівнює діаметру кола і є проекцією діаметра кола,

розташованого на лінії рівня, паралельної до аксонометричної площини П'.

Великий діаметр розташований на проекції лінії рівня. Лінія рівня «збереже» не

тільки довжину діаметра d кола, але й прямий кут із прямою лінією, що їй

перпендикулярна (теорема про проектування прямого кута). Вісь z

перпендикулярна площині Oxy, і виходить, перпендикулярна до будь-якої

прямої цієї площини, у тому числі й лінії рівня. Тоді аксонометрична проекція

лінії рівня, на якій розташований великий діаметр еліпса, перпендикулярна до

проекції осі z – аксонометричної осі z'. Малий діаметр еліпса

перпендикулярний до великого діаметра. При виконанні ізометрії в масштабі

1,22:1великийдіаметрбуде

дорівнювати 1,22d. Малий діаметр

дорівнює0,71d(приймаємобез

висновку). Еліпс будуємо по великому й

малому діаметрах. Повторюючи все

сказане вище, для площин Oxz і Oyz,

одержиморозташуванняеліпсів,

показане на рис. 9.21. Коло t,

розташоване в площині Oxy або їй

паралельній площині, проектується на

П' в еліпс t', що є ізометрією кола t.

Ізометрією кола n, що належить площині

Oxz або їй паралельній площині, буде

еліпс n'.

Рис. 9.21

115

Ізометрією кола k, що належить площині Oyz або їй паралельній площині, буде

еліпс k'. Ізометрії кіл, приналежних площинам Oxy, Oxz, Oyz або їм

паралельним площинам, будуємо в такій послідовності: будуємо ізометрію

центра кола; будуємо великий і малий діаметри; по великому й малому

діаметрам будуємо ряд точок еліпса; точки еліпса з'єднуємо плавною кривою.

Якщо коло належить площині загального положення, то прямої,

перпендикулярної до цієї площини, на ізометрії немає. Тому необхідно на

комплексному кресленні через центр кола провести відрізок прямої

перпендикулярної до площини кола. Потім побудувати ізометрію цього відрізка

й провести великий діаметр перпендикулярно ізометрії цього відрізка, через

ізометрію центра кола. Великий діаметр дорівнює 1,22d, де d – діаметр кола.

Далі, на комплексному кресленні кола взяти будь-яку точку кола і побудувати її

ізометрію.

Тепер на ізометрії є великий діаметр еліпса й одна його точка. Виходить, можна

виконати побудову еліпса по великому діаметру й точці.

2.2. Ортогональна (прямокутна) диметрична проекція

Ортогональна диметрична проекція (диметрія) є ортогональною

аксонометричною проекцією при u = w, v = 0,5u. По формулі (9.1) одержимо:

u = w = 0,94: v = 0,47. За формулою (9.2) визначимо, що кут між осями x' і y'

дорівнює 970 10', кут між осями x' і y' дорівнює 131°25'. Побудова диметрії

точки виконується так само, як показано на рис. 9.15, 9.16. Коефіцієнти

спотворення: u = w = 0,94; v = 0,47. Така диметрія називається точною

(теоретичною). Точно так само, як в ізометрії, вводимо масштаб приведення,

що у цьому випадку дорівнює 1,06:1, тому що 0,94·1,06 ≈ 1.·

Коефіцієнти спотворення при

цьому u = w = 1, v = 0,5.

Диметрія, виконана в

масштабі 1,06:1, називається

приведеною (практичною)

диметрією. На рис. 9.22

показана диметрія куба зі

зрізаною вершиною,

комплексне креслення якого

наведене на рис. 9.17.

Поруч з диметрією дана

схема розташування

Рис.9.22

диметричних осей із

вказівкою коефіцієнтів спотворення і масштабу приведення. На рис. 9.23

показана диметрія кривій k, комплексне креслення якої наведене на рис. 9.19.

116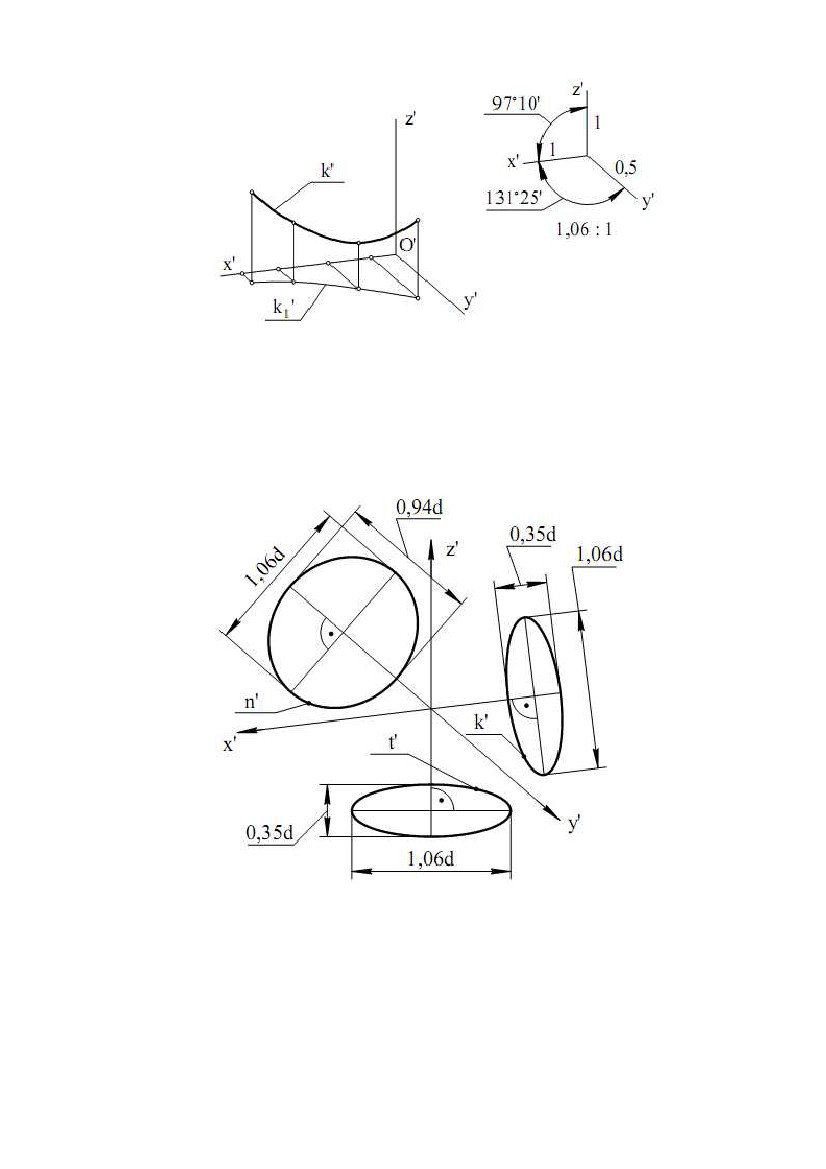

Рис.9.23

Кола t, n, k, розташовані в площинах Oxy, Oxz, Oyz або їм паралельних

площинах, проектуються в еліпси t', n', k' (рис. 9.24). Більші діаметри рівні

1,06d, тому що масштаб приведення 1,06:1. Малий діаметр в t' і k' дорівнює

0,35d, в n' – 0,94d (приймаємо без висновку).

Рис. 9.24

Диметрію кола, що належить площині загального положення, будуємо

так само, як і ізометрія. Великий діаметр еліпса дорівнює 1,06d, де d – діаметр

кола. У побудові ізометрії й диметрії фігури багато спільного, тому що

ізометрія й диметрія - це окремі випадки (конкретні види) прямокутної

аксонометричної проекції, але є й відмінності, викликані тим, що в ізометрії й

диметрії різні коефіцієнти спотворення по осях.

117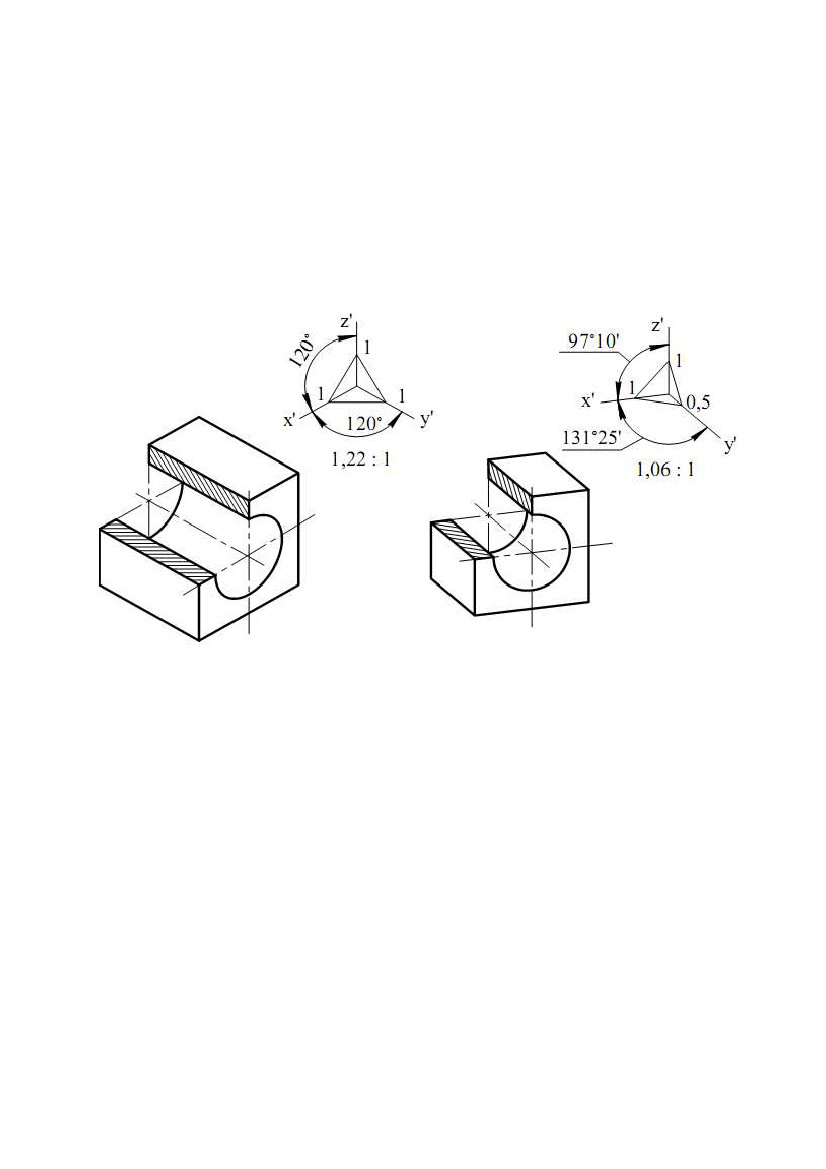

У курсі інженерної графіки при виконанні ізометрії і диметрії деталей для

підвищення наочності робиться виріз частини деталі. На рис. 9.25, 9.26

показана ізометрія й диметрія куба з циліндричним отвором. Напрямок

штрихування в кожній із площин визначається по трикутнику штрихування, що

доданий до зображення осей. Вершини трикутників штрихування лежать на

осях і віддалені від початку координат на відстані, пропорційні коефіцієнтам

спотворення. В ізометрії ці відстані рівні між собою (u = v = w = 1), у диметрії

відстань по осі у два рази менше, ніж по осях x і z (u = w =1, v = 0.5).

Рис.9.25

Рис.9.26

118

10. ЗАДАЧІ ДЛЯ САМОСТІЙНОГО РОЗВ'ЯЗАННЯ

1. Побудувати КК (П1П2П3) точок А(30; 40; 20), В(60; – 40; – 30) (рис. 10.1).

2. Дано точку А(70; 60; 30). Побудувати точку В, симетричну точці А відносно

П1 (рис. 10.2).

3. Дано прямі a║b загального положення. Побудувати пряму h║П1, яка

перетинає a і b і віддалену від П1 на 30 міліметрів (рис. 10.3).

4. Дано А(90; 40; 30), В(10; 15; 20), З(60; 45; 20), D(30; 15; 40). Побудувати

прямі (АВ) і (CD). Записати координати конкуруючих точок (рис. 10.4).

5. Дано площину (∆АВС), проекції D2, E1, F2. Побудувати проекції D1, E2,

F1, якщо D, E, F належать площині (∆АВС) (рис. 10.5).

6. Дано площину (∆DFE). Через точку D провести горизонталь h, через точку F

– фронталь f у цій площині (рис. 10.6).

7. Побудувати точку перетину прямої e і площини (∆АВС), указати видимість

(рис. 10.7).

8. Побудувати лінію перетину площин (∆АВС) і (∆DFE) (рис. 10.8).

9. Побудувати КК правої гвинтової лінії, розташованої на циліндрі і яка

проходить через точку А (один виток), крок гвинтової лінії дорівнює 80

міліметрів (рис. 10.9).

10. Побудувати проекції кола R40, із центром О, що належить площині Σ (рис.

10.10).

11. Побудувати другі проекції точок, що належать сфері (рис. 10.11).

12. Побудувати другу проекцію лінії, що належить конічній поверхні

(рис. 10.12).

13. Побудувати лінію перетину площини Σ і конічної поверхні Γ (рис. 10.13).

14. Побудувати лінію перетину призми і проектуючої площини . (рис. 10.14).

15. Побудувати лінію перетину поверхонь: а) рис. 10.15, б) рис.10.16,

в) рис. 10.17.

16. Визначити натуральну величину (НВ) відрізка і кут його нахилу до

площини П1 (рис. 10.18).

17. Визначити кут між прямою і площиною (рис. 10.7).

18. Визначити кут між площинами (рис. 10.8).

19. Визначити відстань від точки N до прямої (ВС) (рис. 10.19).

20. Визначити кут і відстань між даними прямими (рис. 10.20).

21. Визначити НВ (∆АВС) і побудувати центр вписаного кола (рис. 10.21).

22. Через точку D провести пряму паралельну площині (∆АВС), і яка перетинає

пряму EF (рис. 10.22).

23. Побудувати ізометрію фігури (рис. 10.23).

24. Побудувати диметрію фігури (рис. 10.24).

119

Рис.10.1

Рис.10.2

Рис.10.3

Рис.10.4

Рис.10.5

Рис.10.6

Рис.10.7

Рис.10.8

Рис.10.9

Рис.10.10

Рис.10.11

120

Рис.10.12

Рис.10.13

Рис.10.14

Рис.10.15

Рис.10.16

Рис.10.17

Рис.10.18

Рис.10.19

Рис.10.20

Рис.10.21

Рис.10.22

Рис.10.23

121

Рис.10.24