Курс лекцій НАРИСНА ГЕОМЕТРІЯ. Курс лекцій удк 514. 18 В.І. Лусь. Нарисна геометрія Курс лекцій. Харків хнамг, 2008. 127 с
 Скачать 5.98 Mb.
|
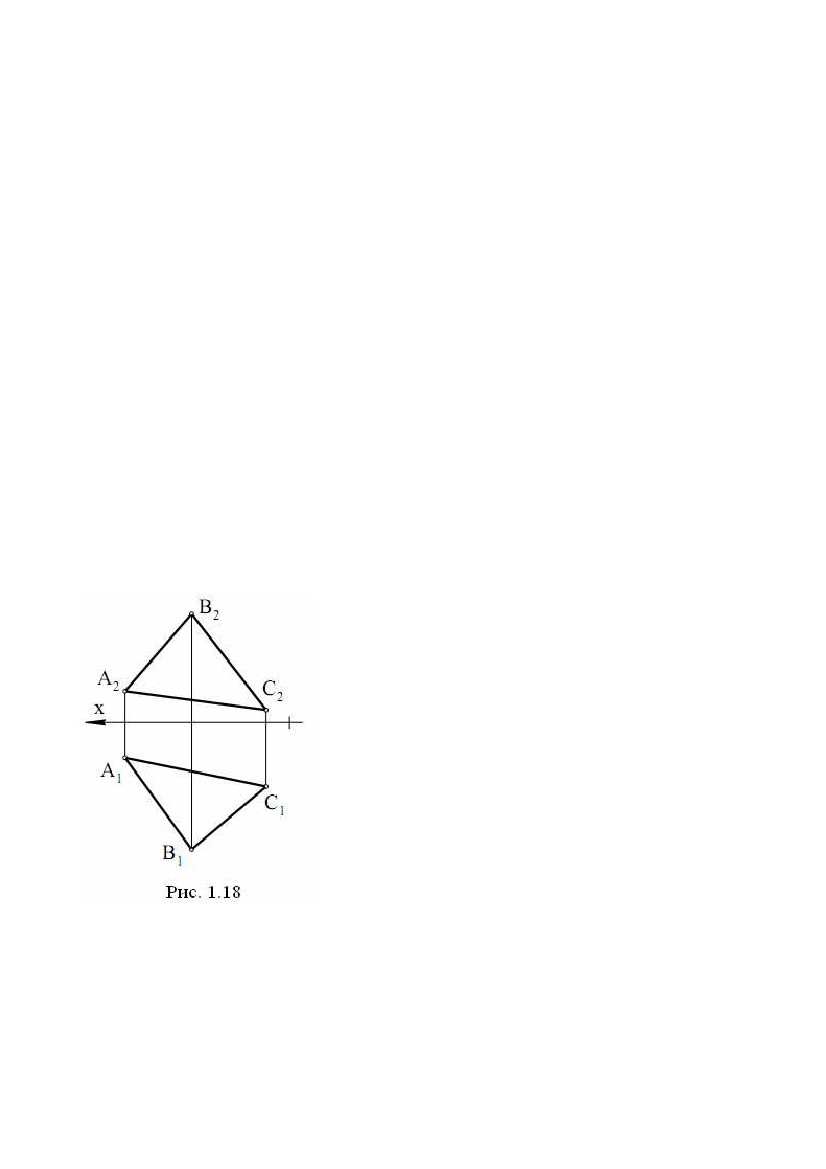 прямої і провести через них профільну проекцію прямої (точніше, профільнупроекцію відрізка, що задає пряму). Звернемо увагу на одну властивість ліній рівня. Відрізок, розташований на лінії рівня, проектується в рівний йому відрізок на ту площину проекцій, якій паралельна лінія рівня. Наприклад, відрізок на горизонталі проектується на горизонтальну площину проекцій у рівний йому відрізок, тобто в натуральну величину (рис. 1.2, = 0). 2.3. Комплексне креслення площини Площина, не перпендикулярна до жодної з площин проекцій, називається площиною загального положення. Площина, перпендикулярна хоча б до однієї із площин проекцій, називається площиною окремого положення. Побудувати комплексне креслення всіх точок площини неможливо, тому що множина точок площини нескінченна й необмежена (відстань між двома точками площини може приймати які завгодно більші значення). Для того щоб побудувати комплексне креслення площини, зробимо так само, як зробили при побудові комплексного креслення прямої. Будемо будувати комплексне креслення частини площини. Звичайно, будь-яка частина (шматок) площини задасть площину на кресленні, але найбільше простою і зручною частиною площини для цієї мети є трикутник. Нехай у площині взято трикутник АВС. При проектуванні ∆АВС на П1 одержимо ∆А1У1С1, при проектуванні на П2 - ∆А2У2С2 (рис. 1.18). Можна сказати, що спочатку побудували комплексне креслення вершин трикутника, а потім однойменні проекції вершин з’єднали відрізками, які є проекціями сторін трикутника. При цьому лінії проекційного зв’язку (А1А2), (В1У2), (С1С2) перпендикулярні до осі X. Таким чином, на рис. 1.18 наведене комплексне креслення площини , заданої трикутником ∆АВС. Для площини , заданої трикутником ∆АВС, будемо використовувати позначення: ; (∆АВС); (∆АВС). Площина Σ (рис. 1.18) є площиною загального положення.∆∆ Переконаємося у цьому, розглянувши комплексні креслення площин окремого положення (рис. 1.19). Площина Г (∆ DFE), перпендикулярна до горизонтальної площини∆ проекцій П1, називається горизонтально - проектуючою площиною. На П1 площину Г проектується в пряму лінію, що є лінією перетину Г і П1 20 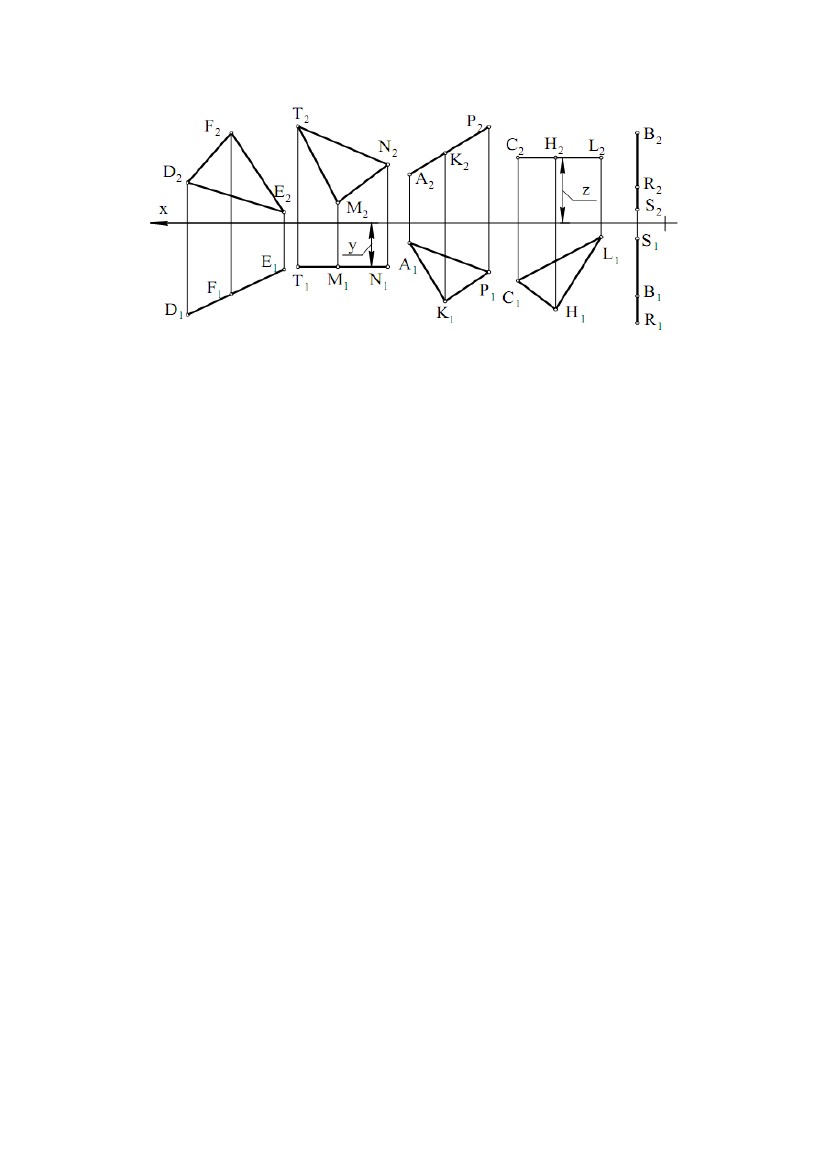 Рис. 1.19Для будь-якої точки площини Г пряма, що проектує цю точку на П1, перебуває в площині Г. Всі точки площини Г проектуються на лінію перетину Г і П1. Трикутник DFE на П1 проектується у відрізок, а на П2 - у трикутник. Відрізок на П1 задає пряму, в яку проектується площина Г. Площина (∆ TNM) теж горизонтально - проектуюча, тому що її горизонтальна проекція – пряма, задана відрізком T1M1. Відрізок T1M1 паралельний осі X. Це значить, що у всіх точок площини (∆TNM) координата Y однакова, тобто площина паралельна фронтальній площині проекцій П1. Така площина називається фронтальною площиною рівня, або фронтальною площиною. Площина (AKF) перпендикулярна до П2 і називається фронтально - проектуючою площиною. На фронтальну площину проекцій ця площина проектується в пряму, задану відрізком A2P2. Фронтально - проектуюча площина (∆CHL) паралельна горизонтальній площині проекцій, тому що координата Z у всіх точок цієї площини однакова (C2L2 ║ x). Така площина називаєтьсягоризонтальною площиною рівня, або горизонтальною площиною. Площина (∆BRC) перпендикулярна до П1 і П2, ця площина∆ перпендикулярна осі X. У системі (П1П2П3) вона називається профільною площиною рівня, або профільною площиною, тому що (∆BRC) ║ П3∆ (координата X всіх точок площини однакова). У системі (П1П2П3), площина, перпендикулярна до профільної площини проекцій П3, називається профільно - проектуючою площиною. Профільна проекція такої площини - пряма. У площин окремого положення хоча б одна проекція - пряма лінія. Площина (рис. 1.18) не має цієї особливості, тому є площиною загального положення. Площина може бути задана не тільки трикутником (рис.1.20). Для завдання площини можна використати три точки (1, рис.1.20), дві паралельні прямі (4, рис.1.20), дві пересічні прямі (3, рис.1.20), точку й пряму (2, рис.1.20), будь-якою плоскою геометричною фігурою (5, рис.1.20), 21 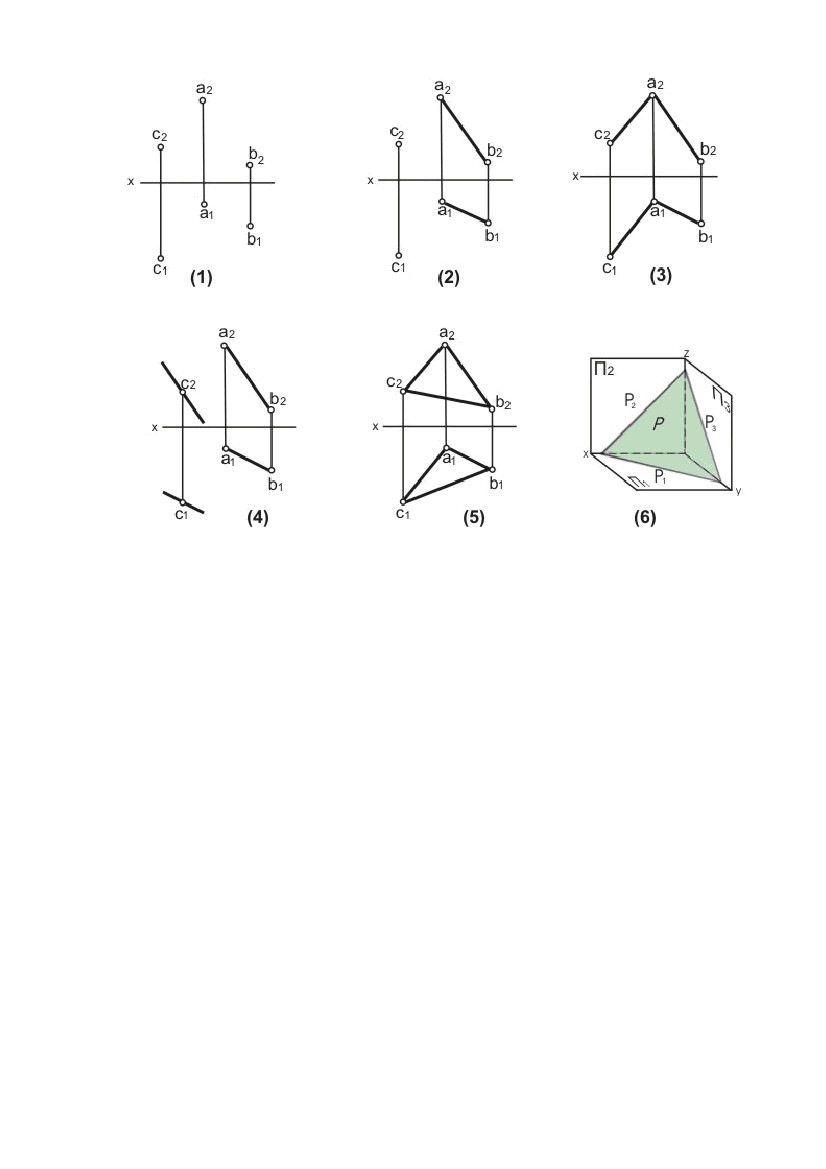 Рис. 1.20слідами (6, рис.1.20), тому що через кожну з цих фігур проходить єдина площина. Звичайно, розглядати таку фігуру як частину площини вже не можна. Від одного способу задання площини можна перейти до будь-якому іншого. Наприклад, якщо площина задана паралельними прямими, те, взявши на одній прямій дві точки, а на іншій прямій - одну точку й з’єднавши ці точки відрізками, перейдемо до задання площини трикутником. Для того щоб від комплексного креслення площини в системі (П1П2) перейти до комплексного креслення площини в системі (П1П2П3), треба побудувати профільну проекцію фігури, що задає площину. 22 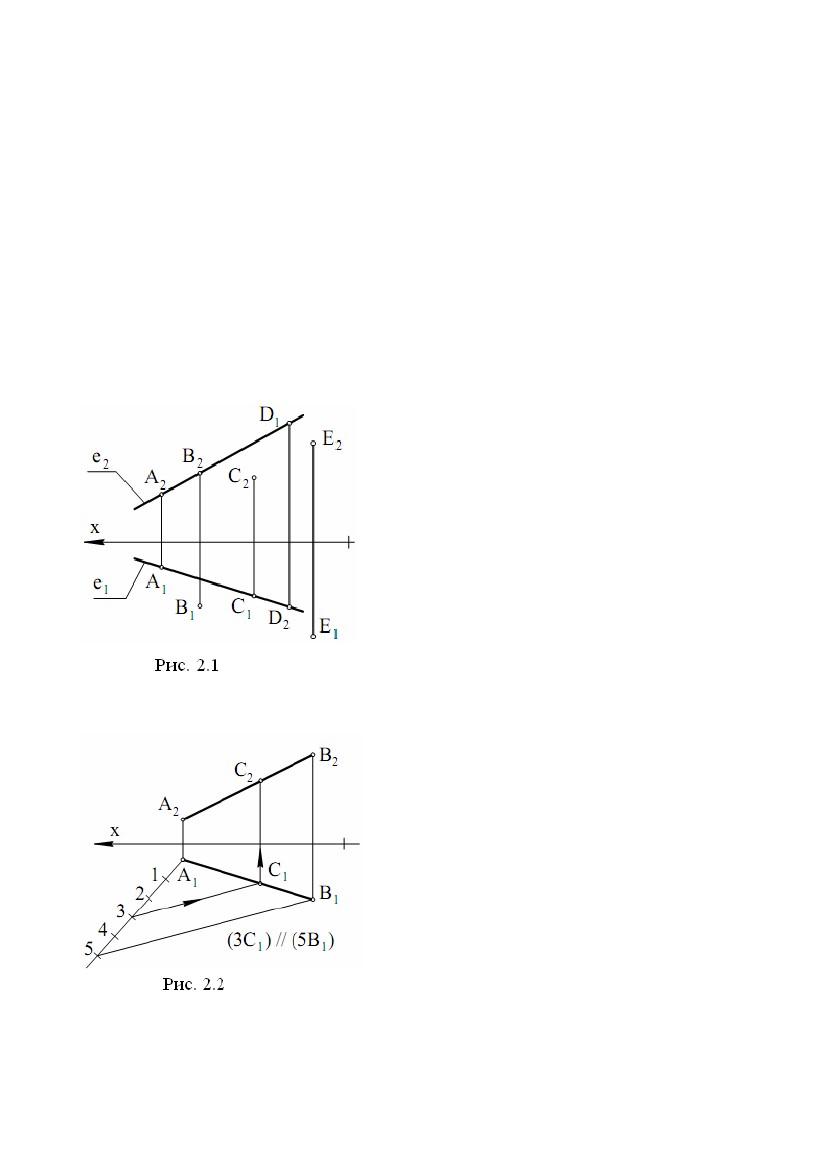 ЛЕКЦІЯ № 2. ВЗАЄМНЕ ПОЛОЖЕННЯ ТОЧОК І ПРЯМИХ, ЇХНЯПРИНАЛЕЖНІСТЬ ПЛОЩИНІ. ПЕРША І ДРУГА ПОЗИЦІЙНІ ЗАДАЧІ. 1. ВЗАЄМНЕ ПОЛОЖЕННЯ ТОЧОК І ПРЯМИХ, ЇХНЯ ПРИНАЛЕЖНІСТЬ ПЛОЩИНІ. 1.1. Взаємне положення точки й прямої. Ділення відрізка прямої в даному відношенні Точка може належати прямій і може не належати прямій. Нехай точка A належить прямій e (A ∈e). При проектуванні прямої і точки на площину П1 одержимо, що горизонтальна проекція точки належить горизонтальній проекції прямої A1 ∈e1. Аналогічно і при проектуванні на П2 - A2 ∈e2. Таким чином, якщо точка належить прямій, те її проекції належать однойменнимпроекціямпрямої. Справедливо і зворотне твердження: якщо проекції точки належать однойменним проекціям прямої, то точка належить прямій. На рис. 2.1 точка A належить прямій e, а інші точки не належать прямій e. Для визначення приналежності точки профільній прямій необхідні профільні проекції точки й прямої. При проектуванні відрізка AB на П1 одержимо відрізок A1B1, при проектуванні на П2 - A2B2. На рис. 2.2 показане комплексне креслення відрізка AB. Оскільки відношення довжин відрізків, що лежать на одній прямій, при проектуванні не міняється, то для ділення відрізка в даному відношенні досить розділити щодо цього одну проекцію відрізка, і це повністю визначить точку ділення. На рис. 2.2 показана побудова точки C, що ділить відрізок AB у відношенні │AC│ : │CB│ = 3:2. На основі теореми Фалеса у відношенні 3:2 ділимо горизонтальну проекцію відрізка, тобто │A1C1│: │C1 B1│= 3:2. Так знаходимо точку C1. Потім по лінії проекційного зв'язку знаходимо C2. 23 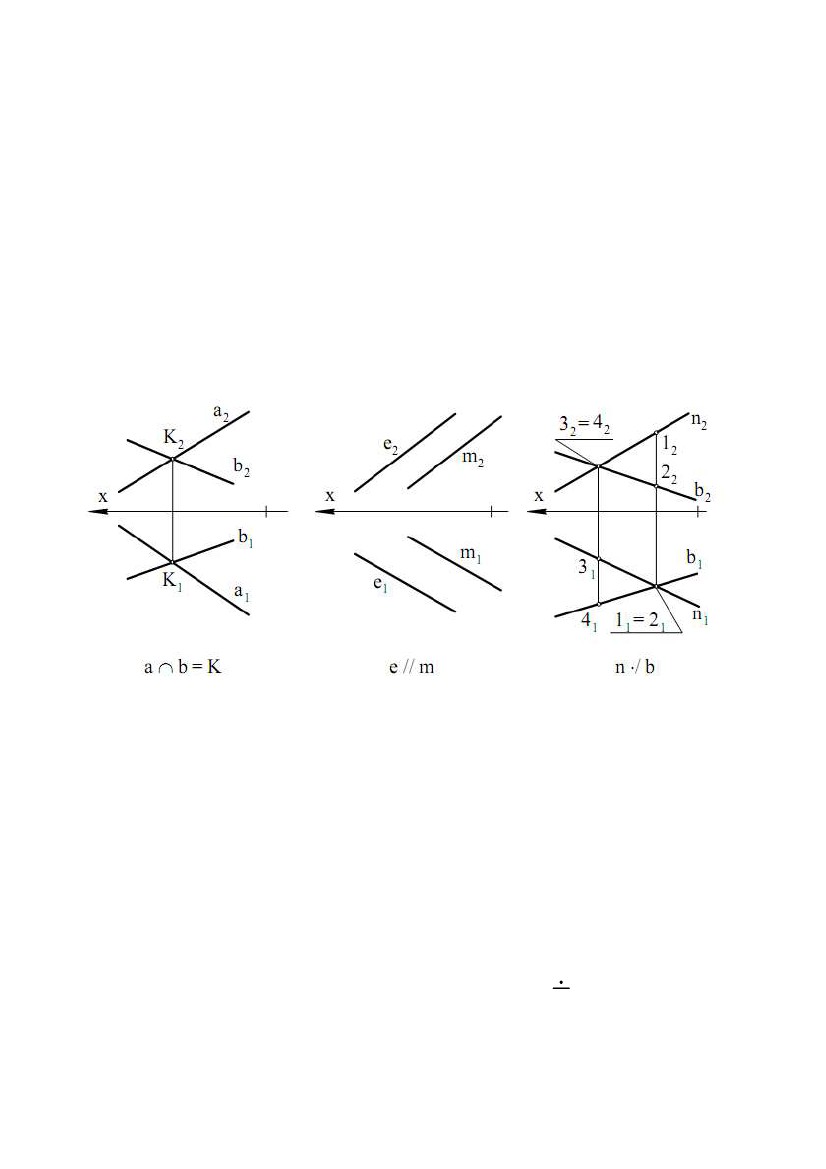 Точка C2 ділить фронтальну проекцію відрізка в тому ж відношенні│A2C2│ : │C2 B2│ = 3:2 (за теоремою Фалеса, тому що лінії проекційного зв'язку всіх точок паралельні). На рис. 2.2 послідовність побудов показана стрілкою на лінії проекційного зв'язку - спочатку будується C1, а потім C2. 1.2. Взаємне положення прямих У просторі дві прямі можуть збігатися, перетинатися, бути паралельними, мимобіжними. У прямих, що збіглися, всі точки збігаються, тому ці прямі матимуть однойменні проекції, що збіглися. По суті, це одна пряма, позначена по-різному. Рис.2.3Рис.2.4Рис.2.5 Пересічні прямі мають одну загальну точку. Нехай прямі загального положення a і b перетинаються в точці K (a ∩b = K). Пересічні прямі в загальному випадку проектуються в пересічні прямі. Точка K - реально існуюча точка, і її проекції перебувають на лінії проекційного зв'язку (K1K2), перпендикулярної осі X (рис. 2.3). Паралельні прямі розташовані в одній площині і не мають загальних точок. Паралельні прямі в загальному випадку проектуються в паралельні прямі (п'ята властивість ортогонального проектування). На рис. 2.4показане комплексне креслення паралельних прямих e і m. При проектуванні цих прямих на П1 одержимо e1 ║ m1, при проектуванні на П2 – e2 ║ m2. Прямі, що не лежать в одній площині, називаються мимобіжними. Ці прямі не паралельні і не перетинаються. Приклад комплексного креслення мимобіжних прямих n і b показаний на рис. 3.5 (n b). Горизонтальні й фронтальні проекції цих прямих перетинаються. Але точки їхнього перетину не лежать на одній лінії проекційного зв'язку. У точці перетину горизонтальних проекцій збіглися проекції двох точок 1 ≡n і 2 ≡b. Це горизонтально конкуруючі точки. Координати X і Y цих точок рівні, а координата Z точки 1 24 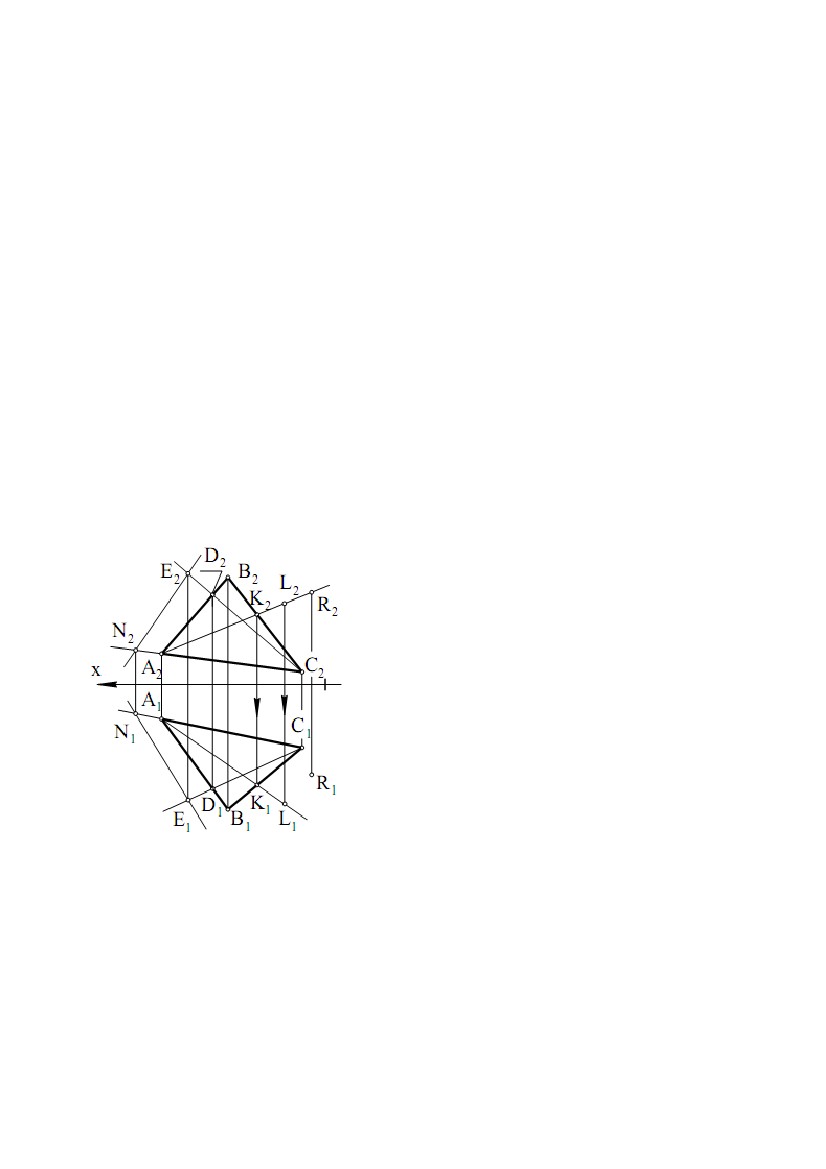 більше, ніж Z точки 2. У точки перетину фронтальних проекцій цих прямихзбіглися проекції двох точок 3 ≡n і 4 ≡b. Це фронтально конкуруючі точки. Координати X і Z цих точок рівні, а координата Y точки 4 більше, ніж y точки 3. Мимобіжні прямі можуть проектуватися на одну площину проекцій у паралельні прямі, а на іншу площину проекцій – у пересічні прямі. Якщо хоча б одна з прямих є профільною прямою, то для визначення взаємного положення прямих потрібно побудувати профільні проекції цих прямих. При розгляді комплексних креслень будь-яких фігур необхідно подумки представляти ці фігури в просторі і їхнє положення щодо площин проекцій. 1.3. Приналежність точки й прямої площині Точка належить площині, якщо вона належить якій-небудь прямій цієї площини. Пряма належить площині, якщо дві її точки належать площині. Ці дві цілком очевидних пропозиції часто називають умовами приналежності точки й прямої площині. На рис. 2.6 площина загального положення задана трикутником АВС. Точки А, В, С належать цій площині, тому що є вершинами трикутника із цієї площини. Прямі (АВ), (ВР), (АС) належать площині, тому що по дві їх точки належать площині. Точка N належить (AC), D належить (AB), E належить (CD) і, виходить, точки N та E належать площині (∆ABC), тоді пряма (NE)∆ належить площині (∆ABC).∆ Якщо задано одну проекцію точки L, наприклад L2, і відомо, що точка L належить площині (∆ABC), то для знаходження другої∆ проекції L1 послідовно знаходимо (A2L2), Рис. 2.6 K2, (A1K1), L1. Якщо умова приналежності точки площині порушена, то точка не належить площини. На рис. 2.6 точка R не належить площині (∆ABC), тому що∆ R2 належить (F2K2), а R1 не належить (A1K1). На рис. 2.7 наведене комплексне креслення горизонтально - проектуючої площини (∆CDE). Точки K і P належать цій площині, тому що P1 і K1 належать∆ прямій (D1C1), що є горизонтальною проекцією площини (∆CDE). Точка N не∆ належить площині, тому що N1 не належить (D1C1). Всі точки площини (∆CDE)∆ проектуються на П1 у пряму (D1C1). Це випливає з того, що площина (∆CDE) ⊥П1. У цьому ж можна переконатися, якщо виконати для точки P∆ 25 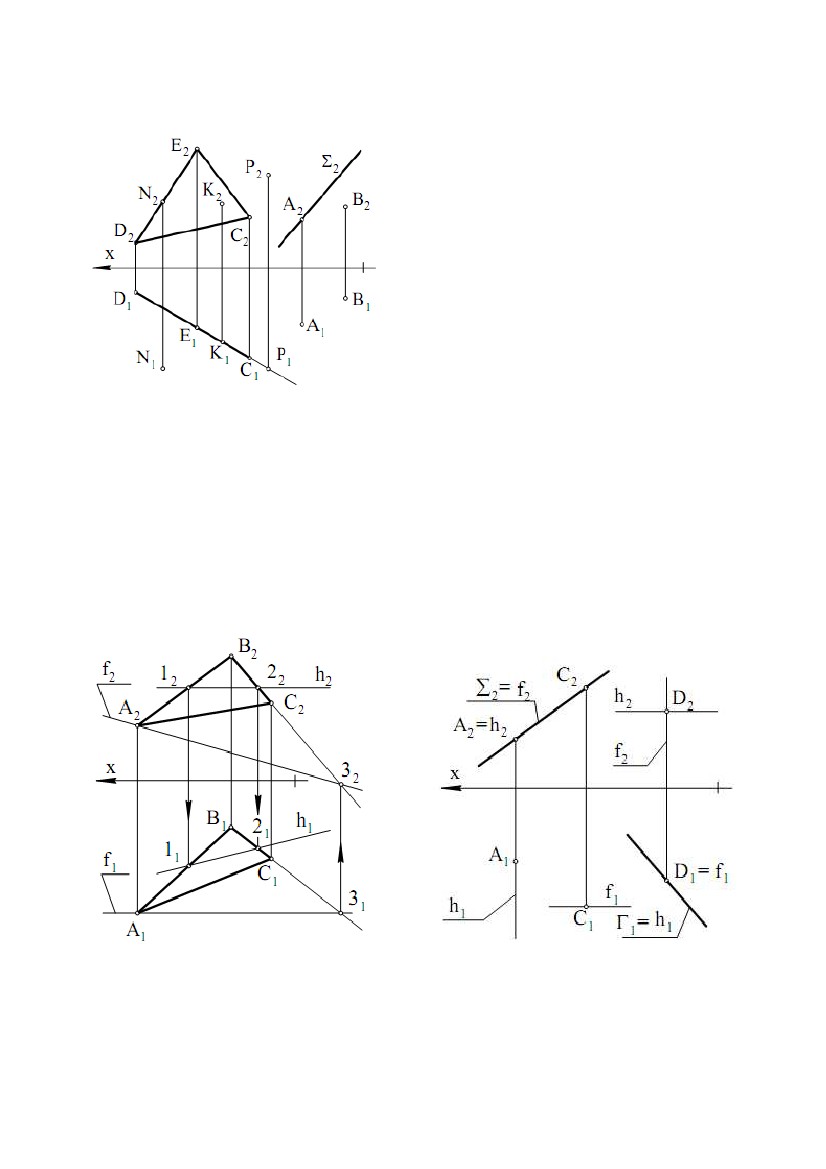 (або будь-якої іншої точки) побудови, які були зроблені для точки L (рис. 2.6).Точка P1 потрапить на пряму (D1C1). Таким чином, для того, щоб визначити приналежність точки горизонтально проектуючійплощині,фронтальна проекція (∆C2D2E2) не потрібна. Тому∆ що надалі проектуючі площини будуть задаватися тільки однією проекцією (прямою лінією). На рис. 2.7 показана фронтально - проектуюча площина ,яка задана фронтальною проекцією Σ2, а також точки A ∈Σ і B ∉ . Взаємне положення точки й площини зводиться до приналежності або не приналежності точки площині. Рис. 2.7 При вирішенні багатьох задач доводиться будувати лінії рівня, що належать площинам загального й окремого положення. На рис. 2.8 показані горизонталь h і фронталь f, що належать площині загального положення (∆ABC). Фронтальна проекція h2 паралельна осі∆ X, тому пряма h - горизонталь. Точки 1 і 2 прямої h належать площині, тому пряма h належить площині. Таким чином, пряма h - це горизонталь площини (∆ABC). Звичайно∆ порядок побудови такий: h2; 12, 22; 11, 21; (1121) = h1. Фронталь f проведена через точку A. Порядок побудови: f1 ║ x, A1∈f1; 31, 32; (A232) = f2. Рис. 2.8 Рис. 2.9 На рис. 2.9 показані проекції горизонталі й фронталі для фронтально проектуючої площини і горизонтально - проектуючої площини Г. У площині горизонталь є фронтально - проектуючою прямою і проходить через точку A (спробуйте уявити горизонталь як лінію перетину і площини, що проходить 26 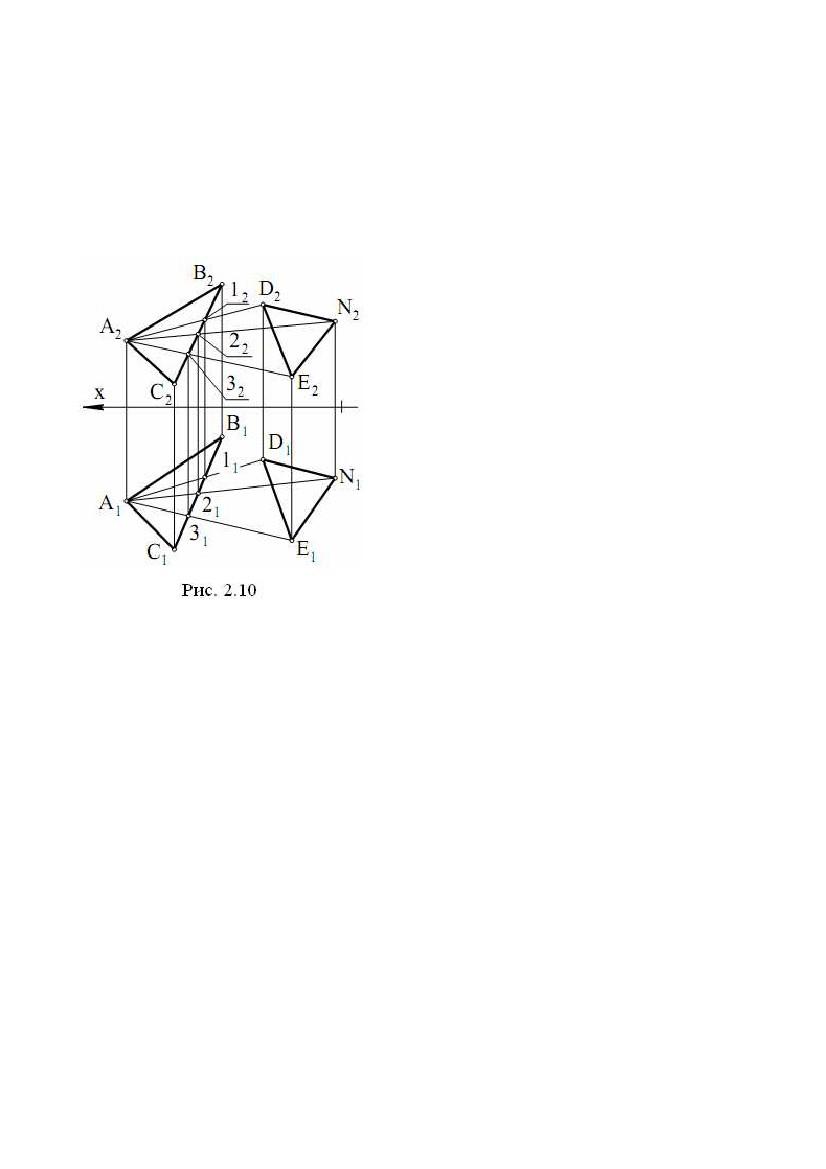 через точку A паралельно П1). Фронталь проходить через точку С. У площині Ггоризонталь і фронталь проведені через одну точку D. Фронталь є горизонтально - проектуючою прямою. З розглянутих вище побудов виходить , що лінію рівня в площині можна провести через будь-яку точку цієї площини. Збіг площин можна трактувати як приналежність однієї площини іншій. Якщо три точки однієї площини належать іншій площині, то ці площини збігаються. Згадані три точки не повинні лежати на одній прямій. На рис.2.10 площина (∆DNE) збігається∆ із площиною (∆ABC), тому що точки D,∆ N, E належать площині (∆ABC).∆ Звернемо увагу на те, що площина , яка задана ∆ABC, тепер може бути задана ∆DNE. Будь-яка площина може бути задана лініями рівня. Для цього необхідно через точку площини (∆ABC) (наприклад∆ через точку А) провести в площині горизонталь і фронталь, які і будуть задавати площину (на рис. 2.10 побудови не показані). Послідовність побудови горизонталі: h2 ║ x (A2 ∈h2); K2 = h2 ∩B2C2; K1 ∩B1C1 (K2K1 ⊥x); A1K1 = h1. Послідовність побудови фронталі: f1 ║ x (A1 ∈f1); L1 = f1 ∩B1C1; L2 ∩B2C2 (L1L2 ⊥x); A2L2 = f2. Можна записати (∆ABC) = (h, f).∆ 2. ПЕРША І ДРУГА ПОЗИЦІЙНІ ЗАДАЧІ Позиційні задачі - це задачі, в яких потрібно визначити положення фігури щодо площин проекцій або взаємне положення фігур - їхню приналежність, паралельність і перетин. 2.1. Взаємне положення прямої і площини Взаємне положення прямої і площини визначається кількістю спільних точок: а) якщо пряма має дві спільні точки із площиною, то вона належить цій площині; б) якщо пряма має одну спільну точку із площиною, то пряма перетинає площину; в) якщо точка перетину прямої із площиною вилучена в нескінченність (невласна), то пряма і площина паралельні. 27 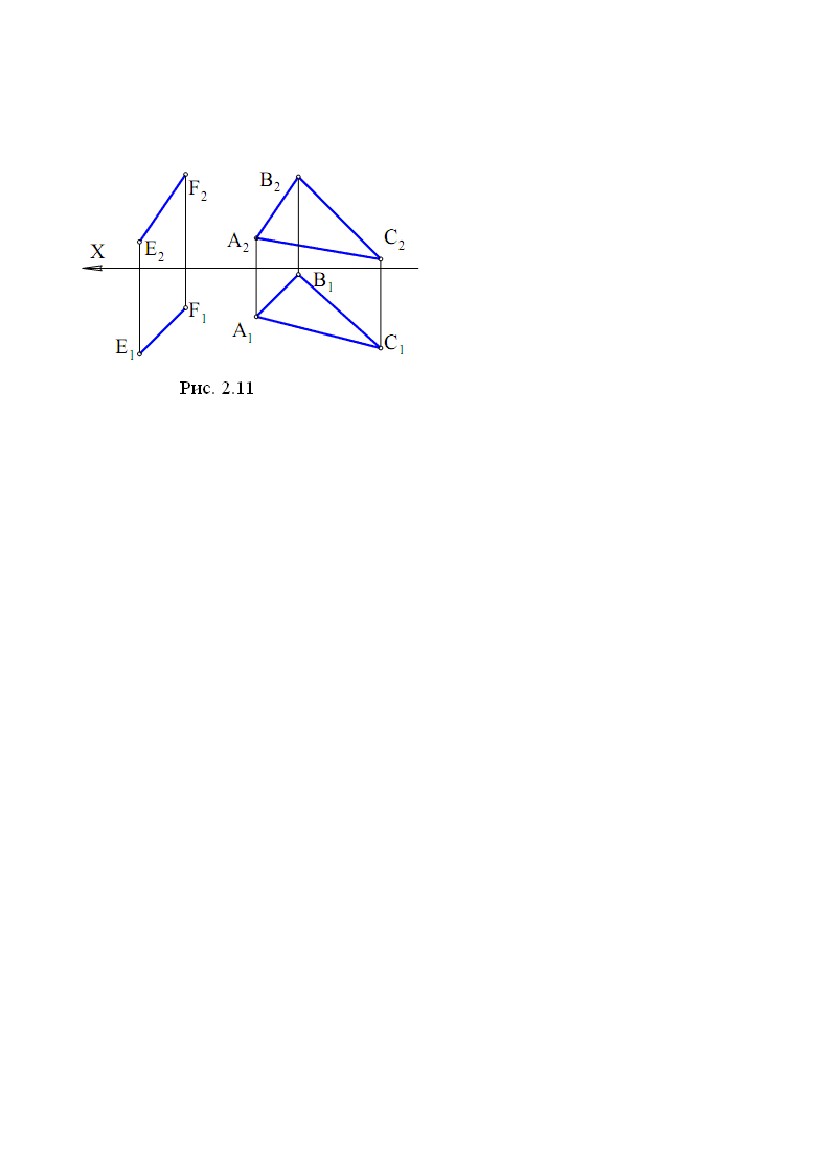 Пряма паралельна площині, якщо вона паралельна якій-небудьпрямій, що лежить у цій площині. Щоб побудувати таку пряму, треба в площині задати пряму й паралельно їй провести потрібну пряму. Нехай площина задана трикутником (∆ABC). Через точку E (рис. 2.11)∆ необхідно провести пряму EF, яка паралельна площині . Для цього через горизонтальну проекцію точки Е(Е1) проведемогоризонтальну проекцію E1F1 шуканої прямої паралельно горизонтальній проекції будь-якої прямої, що лежить у площині , наприклад, прямій AB (E1F1 ║ A1B1). Через фронтальну проекцію E2 точки E паралельно AB проводимо фронтальну проекцію E2F2 шуканої прямої EF (E2F2 ║ A2B2). Пряма EF паралельна площині , заданої трикутником ABC. Пряма буде також паралельна площині, якщо вона лежить у площині, паралельній даній. 2.2. Побудова точки перетину прямої з площиною Задача на побудову точки перетину прямої із площиною, названа першою позиційною задачею, широко застосовується в нарисній геометрії. Вона лежить в основі вирішення наступних задач: • на перетин двох площин; • перетин поверхні із площиною; • перетин прямої з поверхнею; • взаємний перетин поверхонь. Побудувати точку перетину прямої з площиною - значить знайти точку, що належить одночасно заданій прямій і площині. 2.2.1. Площина займає проектуюче положення Якщо площина займає проектуюче положення (наприклад, вона перпендикулярна до фронтальної площини проекцій, рис. 2.12), то фронтальна проекція точки перетину повинна одночасно належати фронтальному сліду площини й фронтальної проекції прямої, тобто бути в точці їхнього перетину. 28 |