динамика. Курсовая работа по динамике исследование колебаний механической системы с одной степенью свободы
 Скачать 0.74 Mb.
|
1.Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы.Изобразим расчетную схему (рис. 2.) 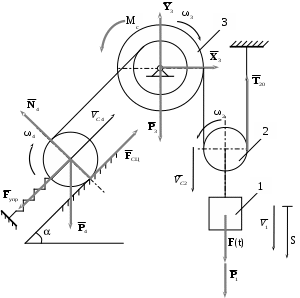 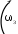 Расчетная схема. На рис. 2 обозначено:  – силы тяжести, – нормальная реакция опорной плоскости, – сила натяжения нити, – упругая реакция пружины, – сила сцепления катка с опорной плоскостью, – реакции подшипника блока 3, – момент вязкого сопротивления, – возмущающая сила.Рассматриваемая механическая система имеет одну степень свободы. Будем определять положение системы с помощью координаты  . Начало отсчета координат совместим с положением статического равновесия груза 1.Для построения дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в форме:
где обозначено: Т – кинетическая энергия системы,  – сумма мощностей внешних сил, – сумма мощностей внутренних сил.Вычислим кинетическую энергию системы как сумму кинетических энергий тел, образующих механическую систему. Груз 1 совершает поступательное движение. Его кинетическая энергия равна:
Блок 2 и каток 4 совершают плоскопараллельное движение, поэтому
где  – момент инерции катка 4. Поскольку блок 2 считаем невесомым, его кинетическая энергия равна нулю.Блок 3 совершает вращательное движение около неподвижной оси. Его кинетическая энергия определяется по формуле:
где  – момент инерции блока 3.Кинетическая энергия всего механизма будет равна:
Так как система имеет одну степень свободы и в качестве координаты, определяющей ее положение, ранее принято перемещение груза 1, то кинематические характеристики всех тел механизма легко выражаются через кинематические параметры груза 1 соотношениями:
Подставляя (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0), (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0), (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) в (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) с учетом (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0), окончательно получаем:
называется приведенной массой. Теперь вычислим правую часть уравнения (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) – сумму мощностей внешних и внутренних сил. Мощность силы равна скалярному произведению вектора силы на скорость точки приложения силы, а мощность момента силы – алгебраическому произведению момента силы на угловую скорость вращения тела, к которому приложен момент:  Знак "+" берется в том случае, если направления момента и угловой скорости одинаковы, а знак "–" если их направления противоположны. Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, не деформируемы и скорости их точек относительно друг друга равны нулю. Поэтому мощности внутренних сил будут равняться нулю  .Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы  Сумма мощностей остальных сил равна: 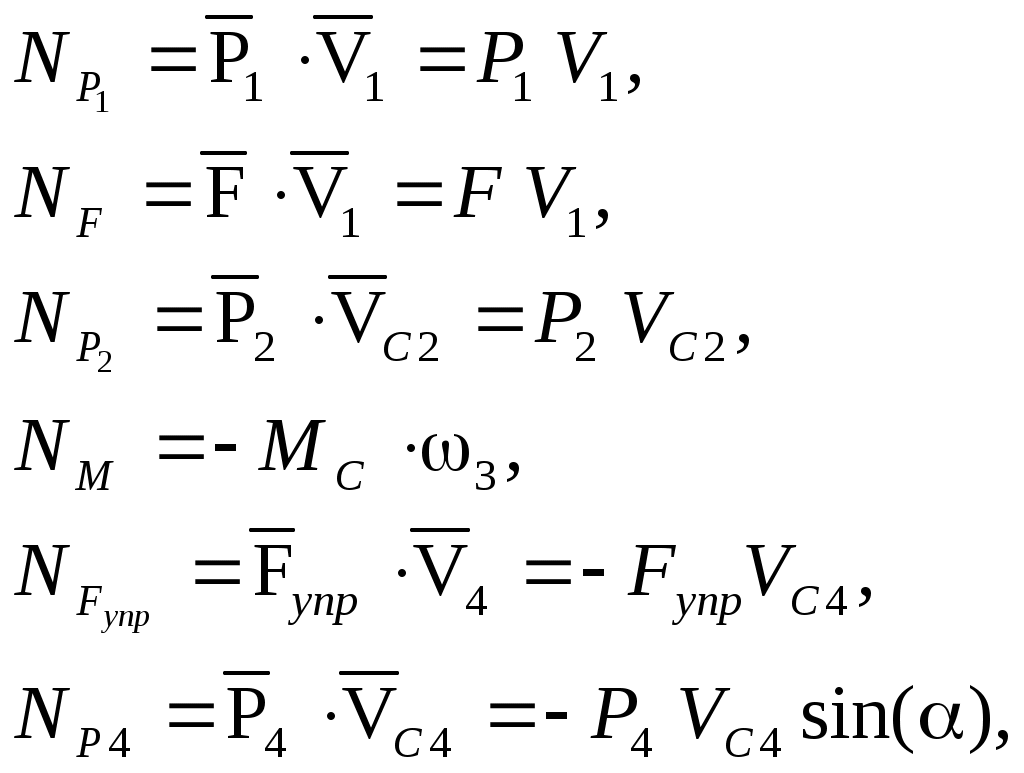 или  .С учетом кинематических соотношений (1.6) сумму мощностей внешних сил преобразуем к виду:
называется приведенной силой. Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение пружины  равно сумме статического  и динамического  удлинений .Тогда упругая сила будет равна:  .Момент вязкого сопротивления  . Тогда приведенная сила (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) в развернутой форме будет определяться выражением:
В состоянии покоя  и условиемравновесия системы будет служить уравнение
Из уравнения (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) определяется статическое удлинение пружины
Таким образом, окончательное выражение для приведенной силы (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) будет иметь вид:
Подставим выражения для кинетической энергии (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) и сумму мощностей всех сил (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)с учетом (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) в уравнение (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0). Тогда, после дифференцирования, получаем дифференциальное уравнение движения системы: 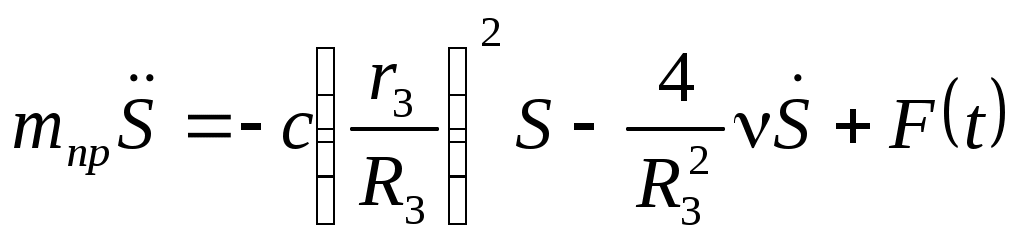 Общепринято такие уравнения представлять в виде:
где введены коэффициенты, имеющие определенный физический смысл:  – частота собственных колебаний, – показатель степени затухания колебаний.Начальные условия:
Уравнения (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0), (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) представляют математическую модель для решения второй задачи динамики. | |||||||||||||||||||||||||||||||||||||||||||||||||
,
,
.
.
.
.
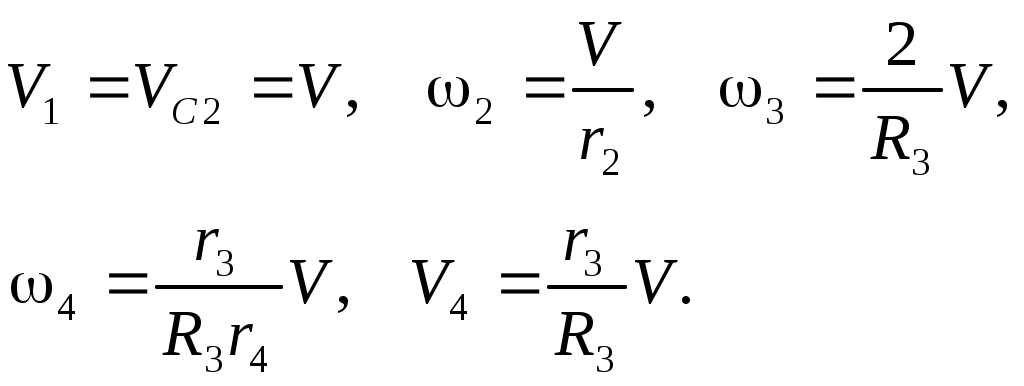
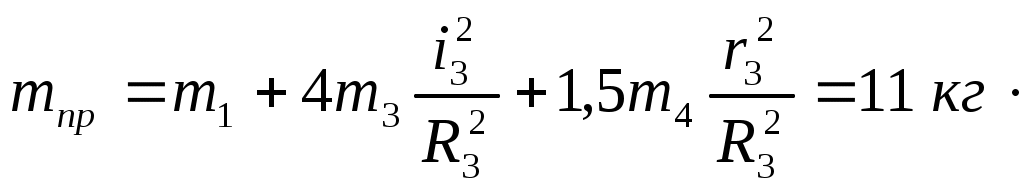
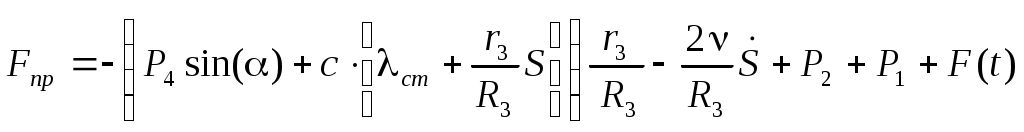