динамика. Курсовая работа по динамике исследование колебаний механической системы с одной степенью свободы
 Скачать 0.74 Mb.
|
5.Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2-го рода.Составим теперь уравнение Лагранжа 2-го рода. В качестве обобщенной координаты примем перемещение груза 1 –  . Для механической системы с одной степенью свободы дифференциальное уравнение движения в обобщенных координатах имеет вид:
где  – кинетическая энергия системы;  – обобщенная сила; – обобщенная координата.Выражение для кинетической энергии системы было найдено ранее (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0):
Для определения обобщенной силы сообщим системе возможное перемещение, при котором координата получит приращение  , и вычислим сумму элементарных работ всех активных сил на возможном перемещении.Такая сумма работ ранее вычислялась (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0): 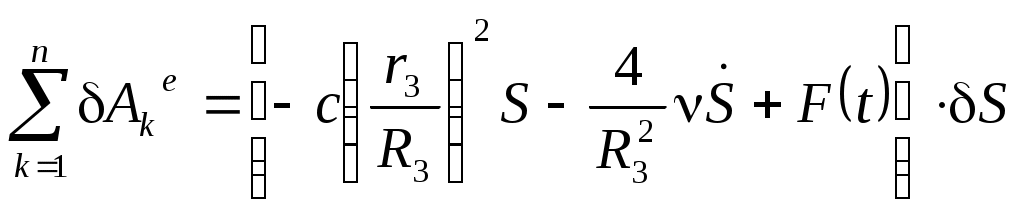 .В тоже время известно, что
Из (Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2-го рода..0) получаем выражение для обобщенной силы:
Подставляя кинетическую энергию (Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2-го рода..0) и обобщенную силу (Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2-го рода..0) в уравнение Лагранжа получаем 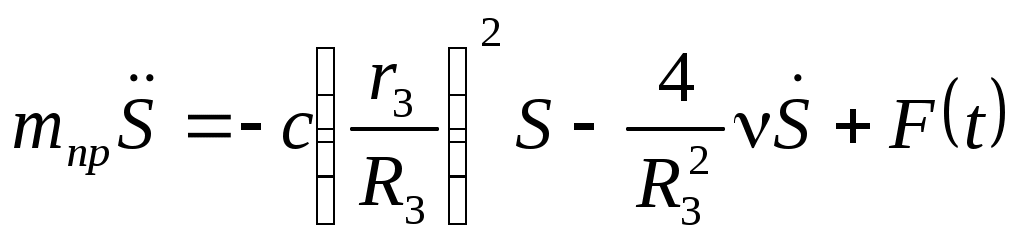 ,или  .6.ПОСТРОЕНИЕ АЛГОРИТМА ВЫЧИСЛЕНИЙ |
,
, 
.
.
.
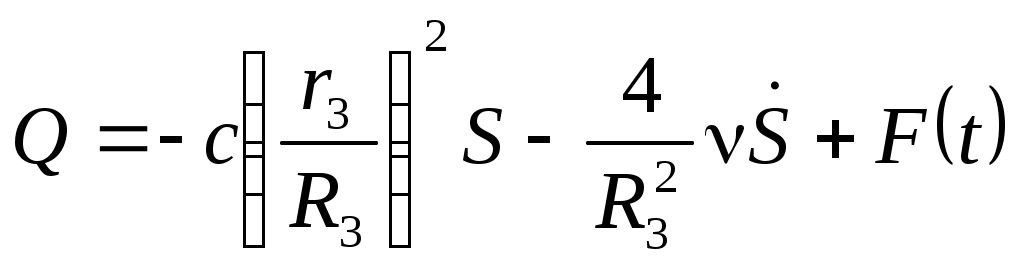