динамика. Курсовая работа по динамике исследование колебаний механической системы с одной степенью свободы
 Скачать 0.74 Mb.
|
4.С |
оставление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.| |  . | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |
Здесь
– сумма элементарных работ всех активных сил на возможном перемещении системы; 
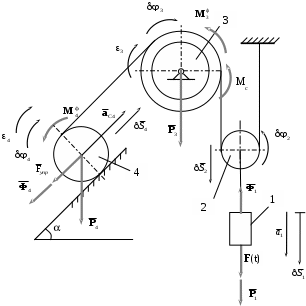
– сумма элементарных работ всех сил инерции на возможном перемещении системы.Изобразим на рисунке активные силы и силы инерции (рис. 4).
Сообщим системе возможное перемещение. Возможная работа активных сил определяется как сумма следующих элементарных работ:
| |  | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |
Сумма элементарных работ указанных сил вычисляется, как и мощность по формуле (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0)
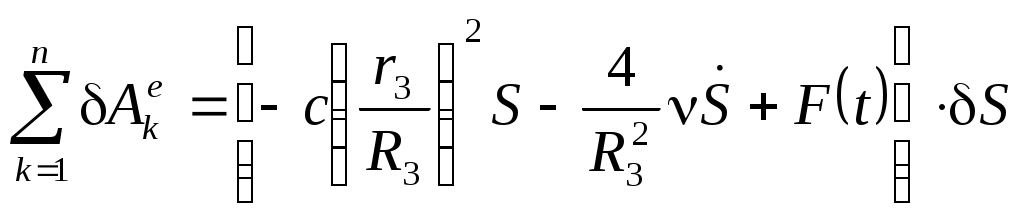| |  | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |
Найдем возможную работу сил инерции:
| |  . | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |
Для величин главных векторов и главных моментов сил инерции имеем следующие выражения:
| |  ,  , ,  . | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |
Используя кинематические соотношения (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0), можно записать
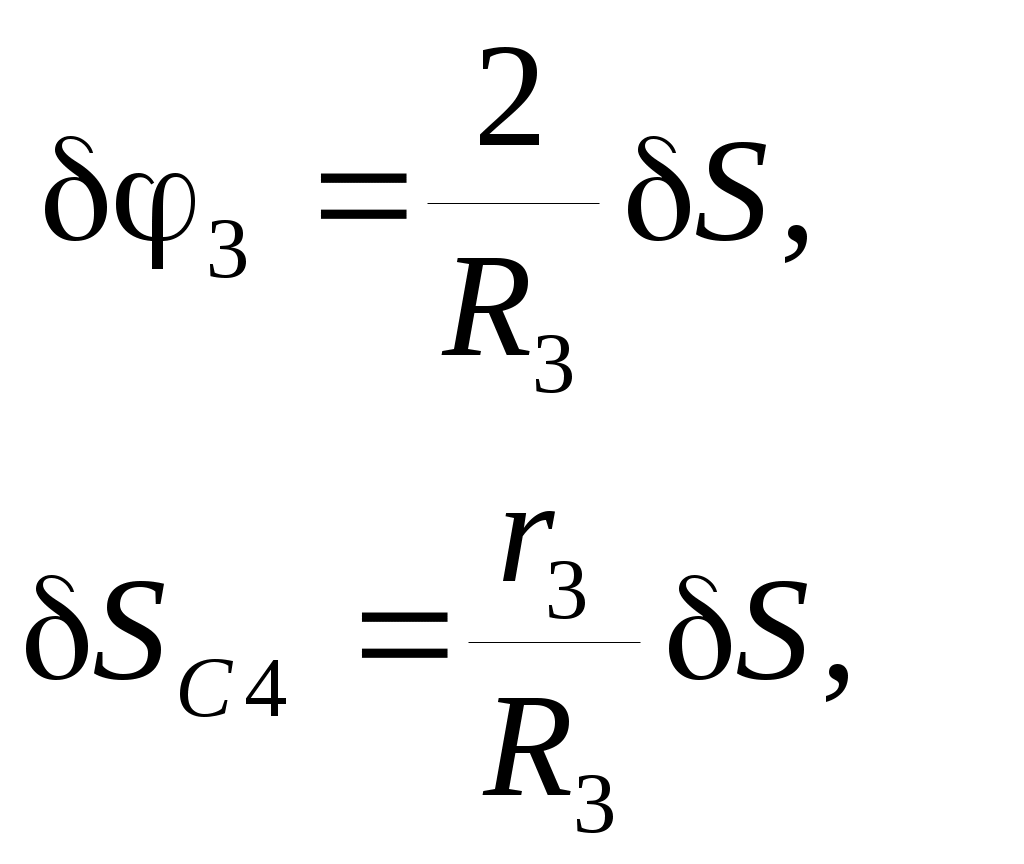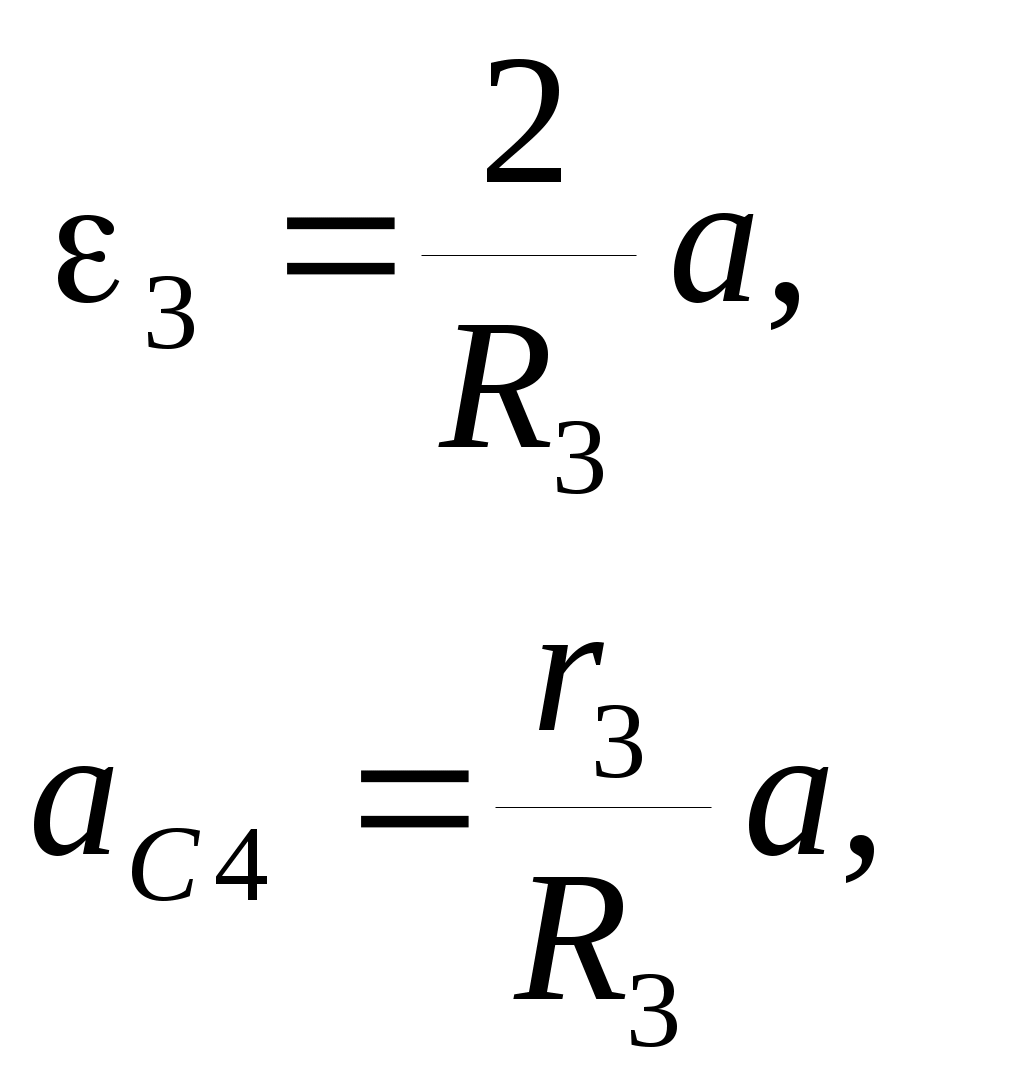| |      | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |
Тогда возможную работу сил инерции можно преобразовать к виду
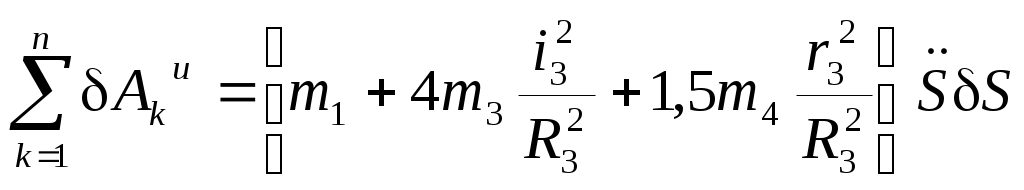| |  , | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |
или
| |  , | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |
где
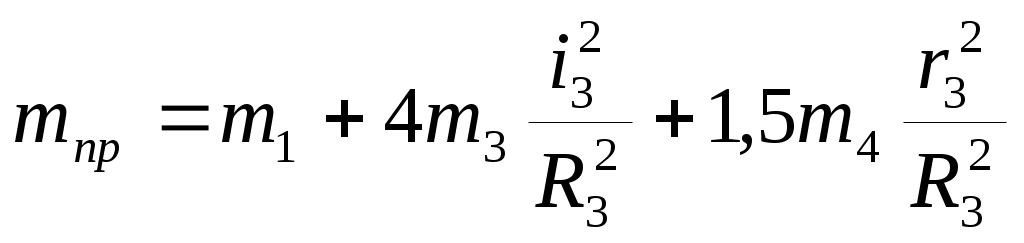.Аналогичное выражение для приведенной массы системы было получено ранее (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0). Подставляя выражения (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) и (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) в общее уравнение динамики (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) получим
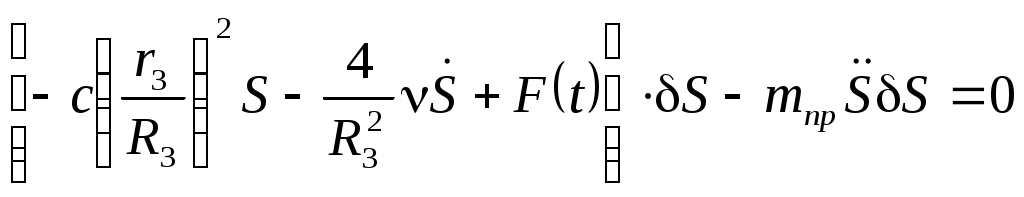| |  . | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |
Разделив (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) на
, получаем дифференциальное уравнение вынужденных колебаний системы:| |  , | (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) |
где
, 
, 
.Дифференциальное уравнение (Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа..0) полностью совпадает с уравнением (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) полученным ранее.