динамика. Курсовая работа по динамике исследование колебаний механической системы с одной степенью свободы
 Скачать 0.74 Mb.
|
2.Определение закона движения системы.Возмущающая сила изменяется по гармоническому закону:  где  – амплитуда возмущающей силы,  – циклическая частота возмущения.Дифференциальное уравнение движения механической системы (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0) с учетом выражения для возмущающей силы примет вид:
где  .Общее решение неоднородного дифференциального уравнения (Определение закона движения системы..0) складывается из общего решения однородного уравнения и частного решения неоднородного. Однородное дифференциальное уравнение, соответствующее неоднородному уравнению (Определение закона движения системы..0), имеет вид:
Решение этого уравнения ищем в виде функции
где  и  – неопределенные постоянные величины.Подставляя (Определение закона движения системы..0) в (Определение закона движения системы..0), получим:  Так как мы ищем нетривиальное решение, то  . Следовательно, должно выполняться условие
Уравнение (Определение закона движения системы..0) называется характеристическим уравнением дифференциального уравнения (Определение закона движения системы..0). Это уравнение имеет два корня:
где  .В этом случае (  ) общее решение уравнения (2.2) имеет вид: Данное выражение нетрудно представить в виде
где  ,  – постоянные интегрирования.Определим частное решение неоднородного дифференциального уравнения (Определение закона движения системы..0). Частное решение ищем в виде правой части
где  .Подставляя (Определение закона движения системы..0) в (Определение закона движения системы..0), после несложных преобразований получим  Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения постоянных  и  : .Решая эту систему алгебраических уравнений, получаем выражения для коэффициентов , и  ,  : ;  ; .Таким образом, решение (Определение закона движения системы..0) найдено. Складывая (Определение закона движения системы..0) и (Определение закона движения системы..0), получаем общее решение неоднородного уравнения (Определение закона движения системы..0)
Подчинив (2.11) и (2.12) начальным условиям, получим систему уравнений относительно искомых констант 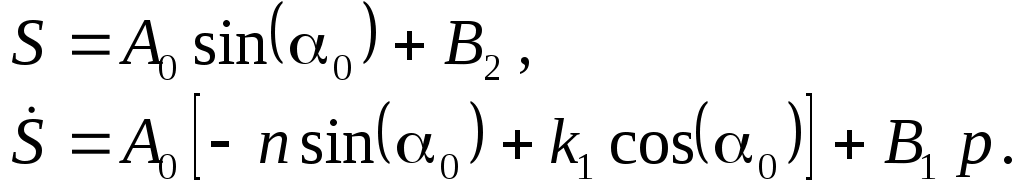 Решая эту систему, получаем:
И, подставляя (Определение закона движения системы..0) в (Определение закона движения системы..0), получаем закон движения механизма, выраженный через перемещение груза  . | ||||||||||||||||||||||||||||||||
,
определяются из начальных условий (Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии механической системы..0). Для этого найдем производную по времени от (Определение закона движения системы..0)
